Лекция №1. Тема 1: Системы линейных алгебраических уравнений. Метод Гаусса решения систем уравнений. Однородные и неоднородные системы уравнений

Вид материала

Подобный материал:

Стр.

Лекция №1.

Тема 1: Системы линейных алгебраических уравнений. Метод Гаусса решения систем уравнений. Однородные и неоднородные системы уравнений.

Задача 1.1. Мальвина задала Буратино задачу: "У Арлекина и Пьеро было всего три яблока. Некто съел все яблоки у Пьеро и столько же яблок у Арлекина, после чего у Арлекина осталось одно яблоко. Сколько яблок было у Арлекина и Пьеро - у каждого по отдельности?"

Решение:

Запишем систему из двух уравнений с двумя неизвестными:

(1)

Попробуйте сначала решить эту систему в уме, а затем записать, как Вы её решали!

Выразим из 1-го уравнения переменную x (x = 3 - y) и подставим полученное выражение во 2-е уравнение: (3 - y) - y =1, откуда 3 - 2y =1, или -2y = -2. Это же уравнение можно было бы получить по-другому - вычесть 1-е уравнение системы из 2-го уравнения: (x - y) - (x + y) = 1 - 3, или -2y = -2. Запишем полученную систему (1-е уравнение - "старое", 2-е уравнение - "новое"):

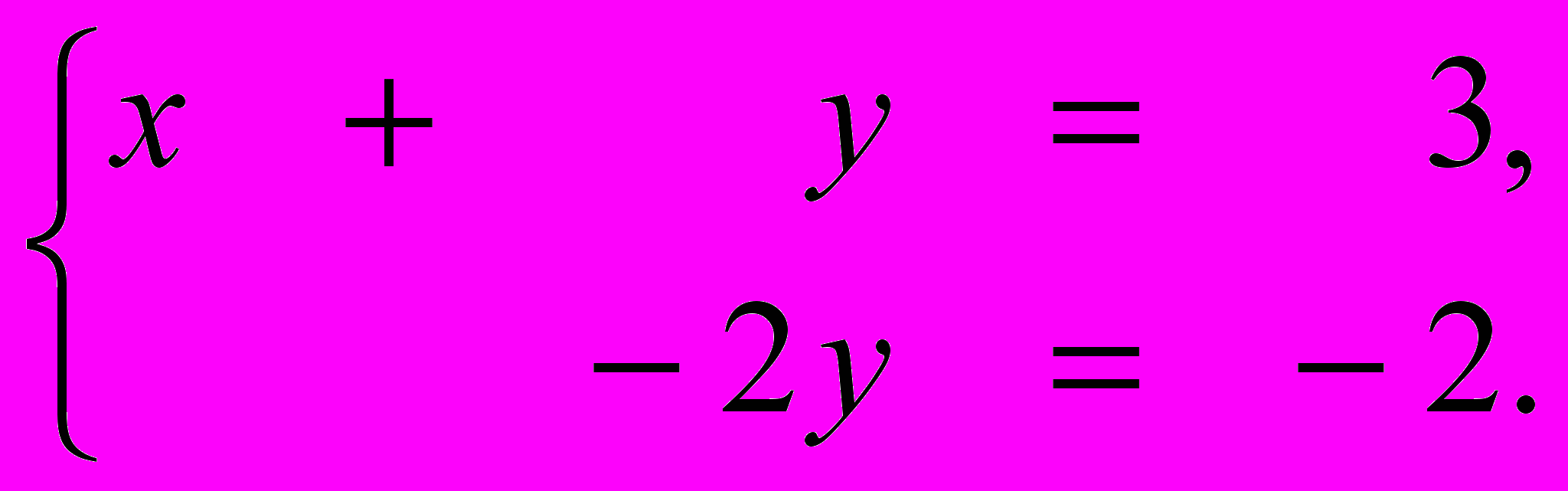
(1а)

Теперь из 2-го уравнения найдём y = 1 и подставим это значение в 1-е уравнение:

x + 1 = 3, откуда x = 2.

Итак, решением системы (1) является пара чисел (x = 2, y = 1).

Ответ:

Неужели Вы сами решали так же долго и нудно?!

Система уравнений, у которой есть хотя бы одно решение, называется совместной. Значит, система (1) - …

Система уравнений, решение которой единственно, называется определенной. Значит, система (1) - …

Какая система называется несовместной? Напишите здесь: ___________

___________________________________________________________________________

Какая система называется неопределенной? Напишите здесь: __________

___________________________________________________________________________

Заканчивая обсуждение задачи 1.1., приведем краткую запись нашего решения:

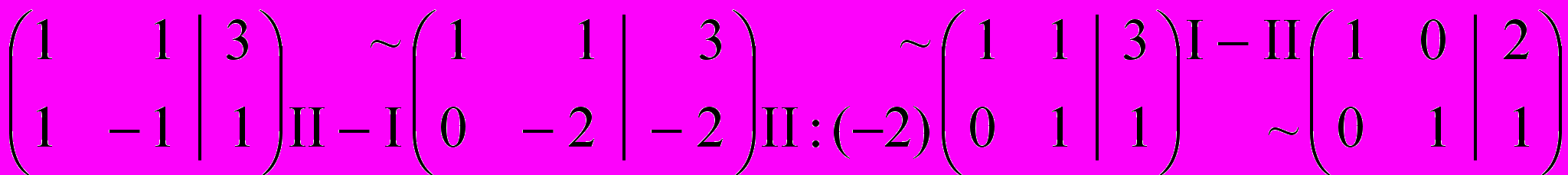
(Римскими цифрами I и II обозначаются, соответственно, 1-е и 2-е уравнения; числа в скобках слева от вертикальной черты - коэффициенты системы при неизвестных x и y; справа от вертикальной черты - свободные члены системы).

Задача 1.2.

Решить систему из 3-х уравнений с тремя неизвестными:

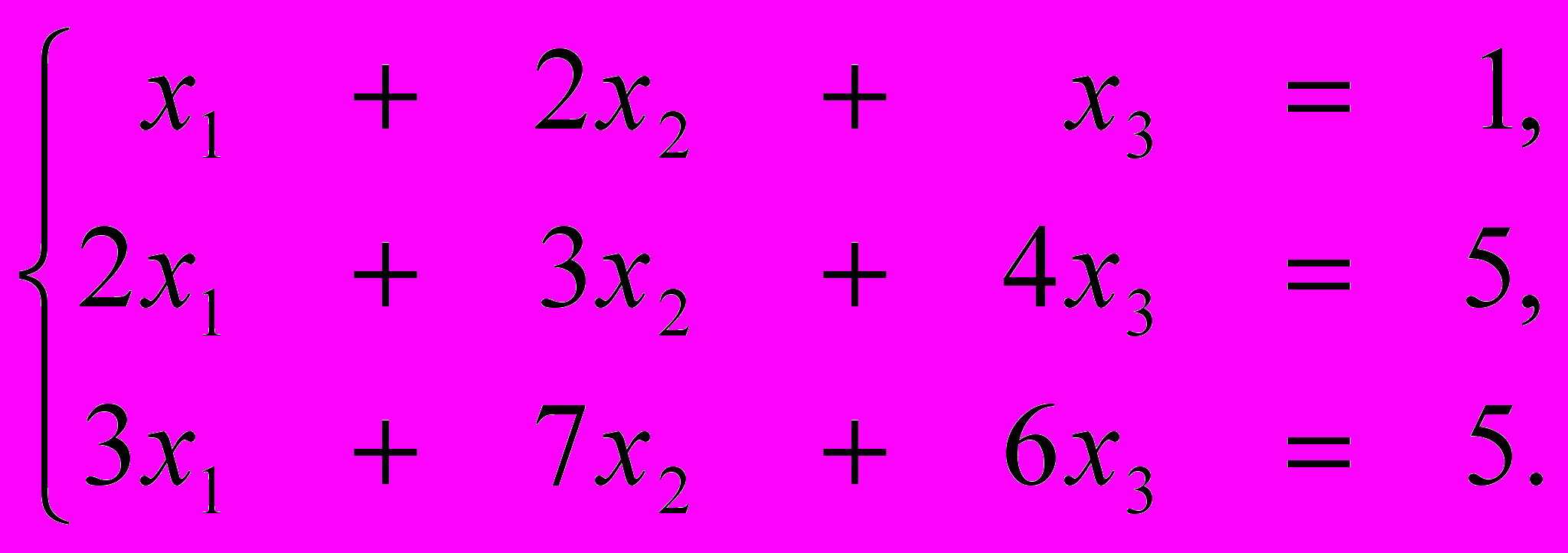
Решение:

Подобно решению задачи 1.1. будем производить действия над строками матрицы системы - таблицы из коэффициентов при неизвестных и свободных членов системы:

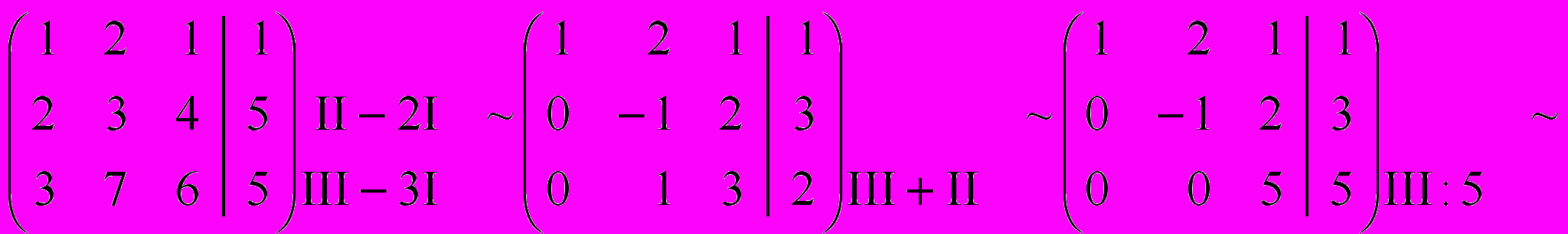
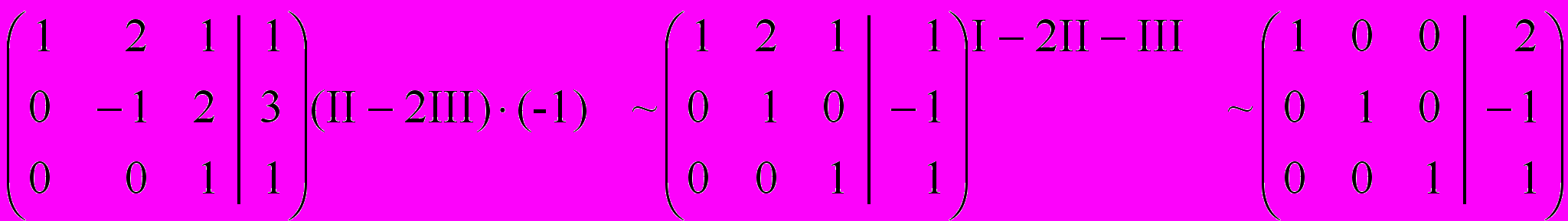
Последней матрице соответствует следующая система уравнений:

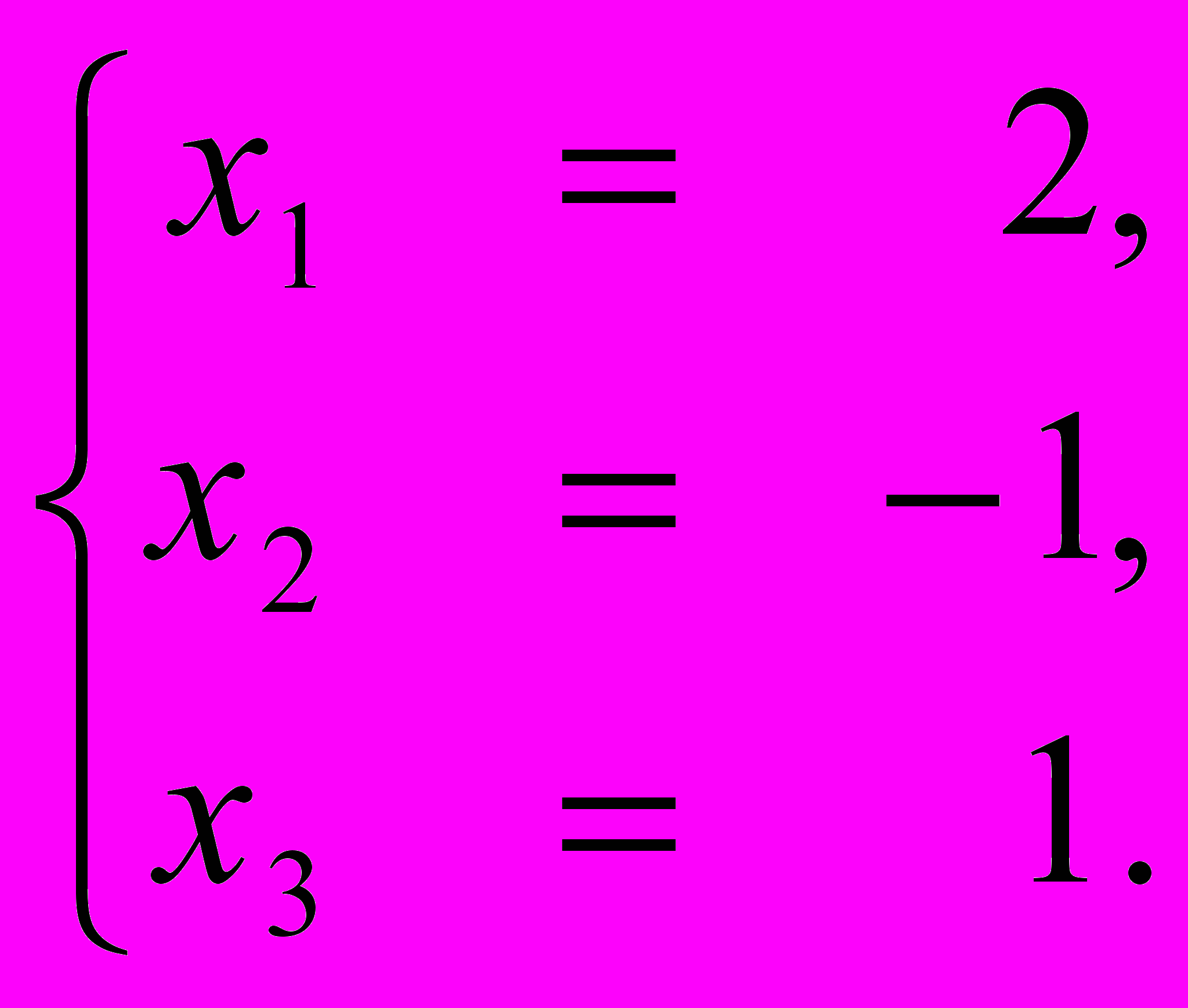
Очевидно ли Вам, что:

решением этой (и исходной) системы является тройка чисел (x₁= 2, x₂ = -1, x₃= 1)?

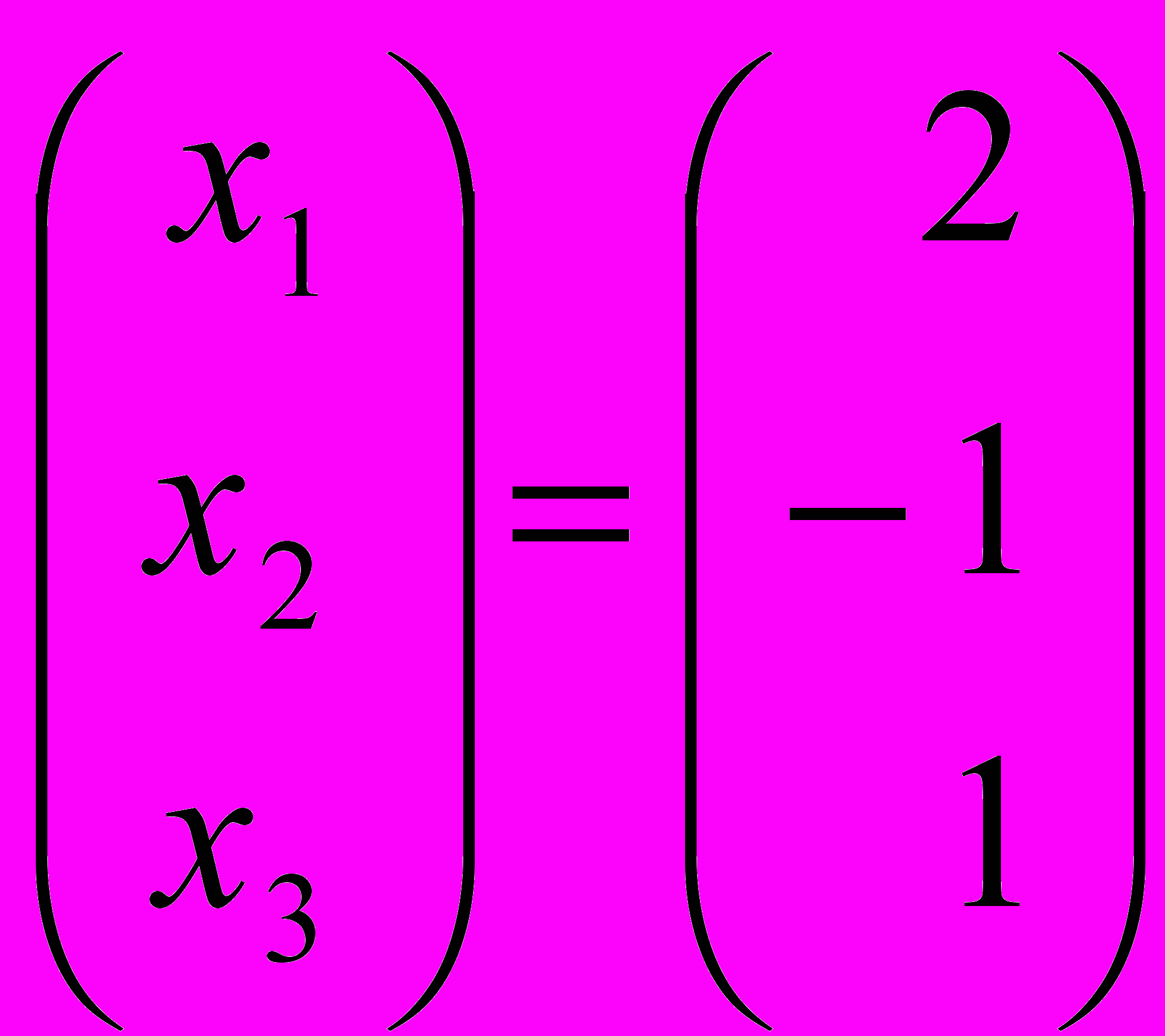
Ответ:

Теперь немного теории:

Системой m уравнений с n неизвестными называется совокупность уравнений следующего вида:

где a_ij, b_i (i = 1, …, m, j = 1, …, n) - заданные числа, x₁, …, x_n - неизвестные (переменные). Числа a_ij называются коэффициентами системы, а числа b_i - свободными членами.

Решением системы называется упорядоченный набор n чисел (с₁, …, с_n), при подстановке которых в систему вместо неизвестных (x₁, …, x_n₎каждое уравнение обращается в тождество (т.е. в верное числовое равенство). Решить систему означает найти множество всех её решений.

Вспомните! -

Система называется совместной, если …

Система называется несовместной, если …

Система называется определенной, если …

Система называется неопределенной, если …

Система называется однородной, если все свободные члены равны 0.

Система называется неоднородной, если (напишите сами): __________________

Таблица, составленная из коэффициентов системы a_ij, называется (основной) матрицей системы; свободные члены системы образуют матрицу-столбец свободных членов; таблица, составленная из коэффициентов системы a_ij и свободных членов b_i, называется расширенной матрицей системы.

j-й столбец

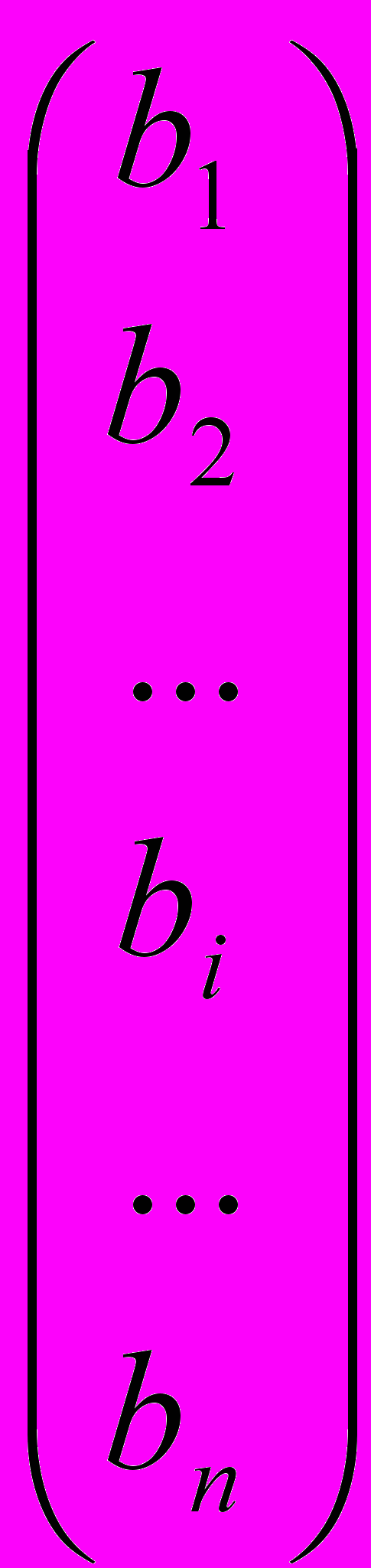
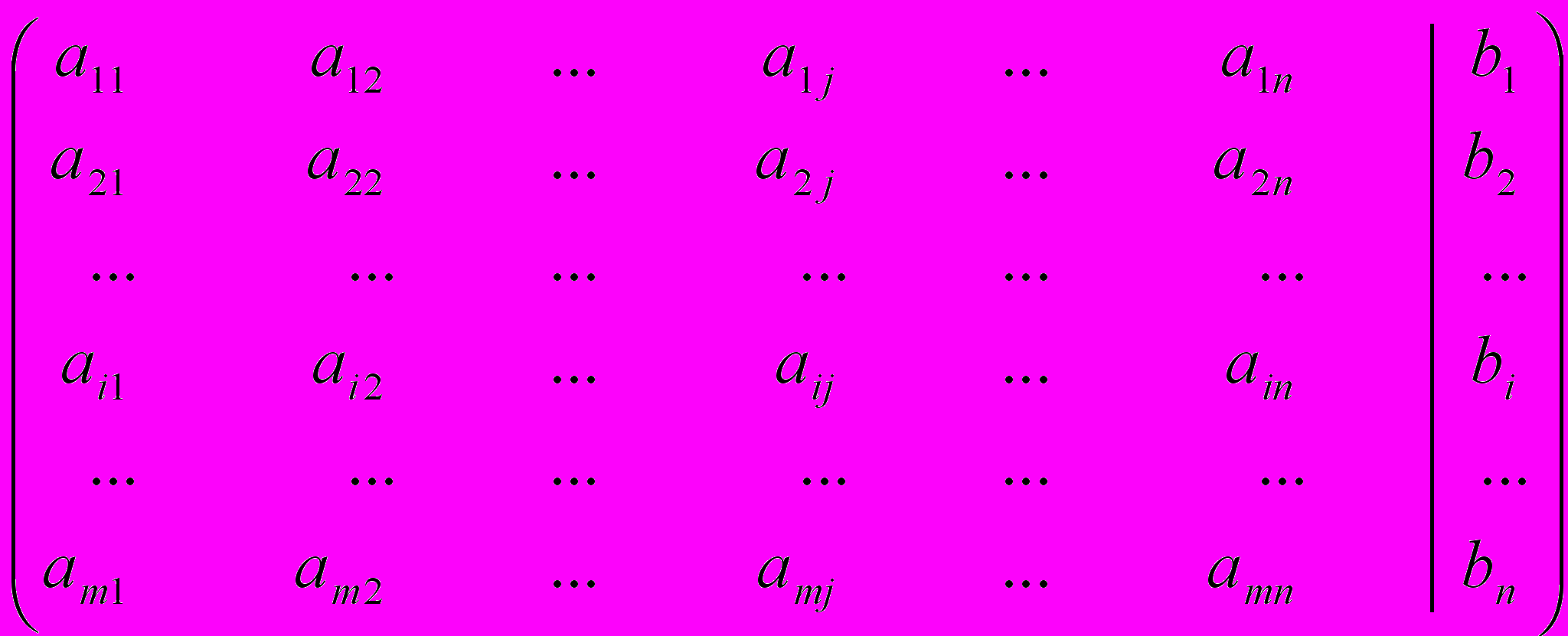
i-я строка

(основная) Матрица системы Столбец

свободных

Расширенная матрица системы членов

Две системы линейных алгебраических уравнений с одинаковым количеством неизвестных называются эквивалентными, если множества решений этих систем совпадают.

Элементарными преобразованиями системы уравнений называются действия следующего вида:

1) перестановка двух уравнений системы (перемена местами);

2) умножение какого-либо уравнения системы на число  0;

3) прибавление к одному уравнению системы другого уравнения системы, умноженного на произвольное число.

Теорема 1.1.

Элементарные преобразования системы линейных алгебраических уравнений приводят её к эквивалентной системе.

Доказательство:

1), 2) - самостоятельно!

3) Пусть в системе (I) первое уравнение умножили на некоторое число с и прибавили ко второму уравнению, в результате чего получилась система (II).

Напишите здесь первое и второе уравнения систем (I) и (II):

1-е:

(I)

2-е

1-е:

(II)

2-е:

Докажем, что каждое решение системы (I) является решением системы (II) и наоборот, каждое решение системы (II) является решением системы (I).

а) Пусть некоторый набор чисел (с₁, …, с_n) является решением системы (I). Это значит, что, в частности, …

напишите сами:

Подставим этот набор в каждое уравнение системы (II). Очевидно, все уравнения, начиная с третьего, обращаются в тождества (объясните!) А при подстановке этого набора в первое и второе уравнения системы (II) получим: …

напишите сами:

Таким образом, указанный набор чисел является решением и системы (II), то есть каждое решение системы (I) является решением и системы (II).

б) Пусть некоторый набор чисел (с₁, …, с_n) является решением системы (II). Остальное напишите сами:

Что и требовалось доказать.

Метод Гаусса - первый из трёх изучаемых нами методов решения системы уравнений - заключается в том, что с помощью последовательности элементарных преобразований из исходной системы получают эквивалентную систему, решение которой либо очевидно, либо отыскивается значительно проще, чем решение исходной системы.

Blog

Лекция №1. Тема 1: Системы линейных алгебраических уравнений. Метод Гаусса решения систем уравнений. Однородные и неоднородные системы уравнений