Метод касательных гиперплоскостей для решения систем нелинейных алгебраических уравнений

Вид материала

Документы

Подобный материал:

• Практических: 0 Лабораторных:, 21.53kb.
• Решение систем нелинейных алгебраических уравнений, 20.84kb.
• Решение систем нелинейных уравнений, 119.58kb.
• Расшифровка : Наука в целом (информационные технологии 004), 79.71kb.
• Лекция № Тема 1: Системы линейных алгебраических уравнений. Метод Гаусса решения систем, 50.61kb.
• Темы курсовых работ по курсу «Программирование» для студентов группы биб-11-1 (2011-2012, 85.51kb.
• Точные решения некоторых нелинейных эволюционных уравнений, встречающихся при описании, 28.05kb.
• Решение систем линейных алгебраических уравнений методом прогонки, 112.31kb.
• Линейных алгебраических уравнений ax=B, где, 66.22kb.
• Название читаемого курса, 134.62kb.

Д.А. КОШУТИН, Е.А. ЗУБКОВА

Научный руководитель – М.В. ПЧЕЛИНЦЕВ, ст. преподаватель

Снежинская государственная физико-техническая академия


МЕТОД КАСАТЕЛЬНЫХ ГИПЕРПЛОСКОСТЕЙ
ДЛЯ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ


В работе предлагается численный метод решения систем нелинейных алгебраических уравнений.


Хорошо известен геометрический смысл метода Ньютона для решения систем нелинейных алгебраических уравнений [1,2]. Рассматривая двумерный пример, будем использовать терминологию многомерного пространства.



Рис.1 Рис.2 Рис.3

Пусть (рис.1) – искомое решение, – начальное приближение к , , – гиперповерхности уровня, проходящие через точку ,, – гиперповерхности нулевого уровня. По прямым, продолжающим градиенты в точке a₀, делаются одномерные ньютоновские шаги , . Через точки , проводятся гиперплоскости, ортогональные соответствующим градиентам. Точка a₁ пересечения этих гиперплоскостей принимается за следующее приближение к . Процесс повторяется из точки а₁ и так далее.

Заметим, что если один из ньютоновских шагов будет сравнительно небольшим (рис. 2), то очередное приближение идет не к решению , а в сторону. Предлагается следующая стратегия (рис. 3). Прямые, продолжающие градиенты, проводятся до пересечения с гиперповерхностями нулевого уровня. В точках пересечения восстанавливаются касательные гиперплоскости, точка пересечения которых принимается за очередное приближение. Эвристически можно ожидать, что очередное приближение будет близким к решению . Известно, что метод Ньютона хорошо сходится, когда начальное приближение достаточно близко к искомому решению. Опыт показывает, что предлагаемый метод имеет меньшую локальную скорость сходимости – разумнее его использовать как метод продолжения [1] или квазиньютоновскую схему [2].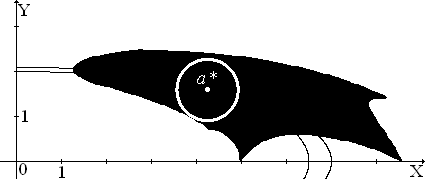



Рис. 4 Рис. 5

Рис. 4. Изображены области сходимости. Сплошным черным цветом показана область сходимости метода Ньютона (для системы нелинейных алгебраических уравнений). Белая окружность является границей шаровой области сходимости. Рис. 5. Черным цветом показана область сходимости двухэтапного процесса. Она почти полностью захватывает область сходимости метода Ньютона и простирается вверх в виде практически не сужающегося “столба”, высота которого неизвестна (экспериментально проверенная высота – 150 единиц).

В заключение отметим, что линейная зависимость градиентов, делающая невозможным применение метода Ньютона и его модификаций, для МКГП, в общем случае, препятствием не является.

Список литературы

1.  Ортега Дж., Рейнболдт В. Итерационные методы решения нелинейных систем уравнений со многими неизвестными. (J. Ortega and W. Rheinboldt. Iterativ Solution of Nonlinear Equations in Several Variables) // М.: Мир, 1975. 558 с.

2.  Дэннис Дж., Шнабель Р. Численные методы безусловной оптимизации и решения нелинейных уравнений (J.E. Dennis, R.B. Shnabel. Numerical Methods for Unconstrained Optimization and Nonliner Equations) // М.: Мир, 1988. 440 с.