Расшифровка : Наука в целом (информационные технологии 004)

Вид материала

Содержание

Ключевые слова
Экран оценки творческого уровня работы
Математическая модель
Метод хорд
Метод половинного деления
Реализация плана исследований.

Подобный материал:

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОУВПО «Самарский государственный архитектурно-строительный университет»

Факультет информационных систем и технологий

Кафедра прикладной математики и вычислительной техники

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОЙ РАБОТЕ

по дисциплине

ТЕХНОЛОГИЯ ПРОФЕССИОНАЛЬНОЙ ДЕЯТЕЛЬНОСТИ

на тему

«Методы решения нелинейных уравнений»

I СЕМЕСТР I КУРС

Научный руководитель Давыдова Евгения Сергеевна

Преподаватель Пиявский Семен Авраамович

Методический руководитель Пиявский Семен Авраамович

	Выполнил: студент ГИП-109 Сафонова Кристина Владиславовна
	подпись 26.12.2009 г.

Оценка преподавателя _______________

Оценка комиссии по результатам защиты_______________

2009 г.

УДК 004.023

Расшифровка:

Наука в целом (информационные технологии - 004)

Методы решения задач

Эвристические методы

Ключевые слова

Исследование, НЛУ, методы решения нелинейных уравнений, метод Ньютона, метод касательных, метод хорд, метод половинного деления, нелинейные уравнения

Реферат

Были найдены три метода решения НЛУ. Они были описаны, затем были реализованы, и была сравнена скорость сходимости и точность на нескольких примерах. Вручную был решен конкретный простой пример всеми тремя методами и сравнены результаты и особенности методов.

Экран оценки творческого уровня работы

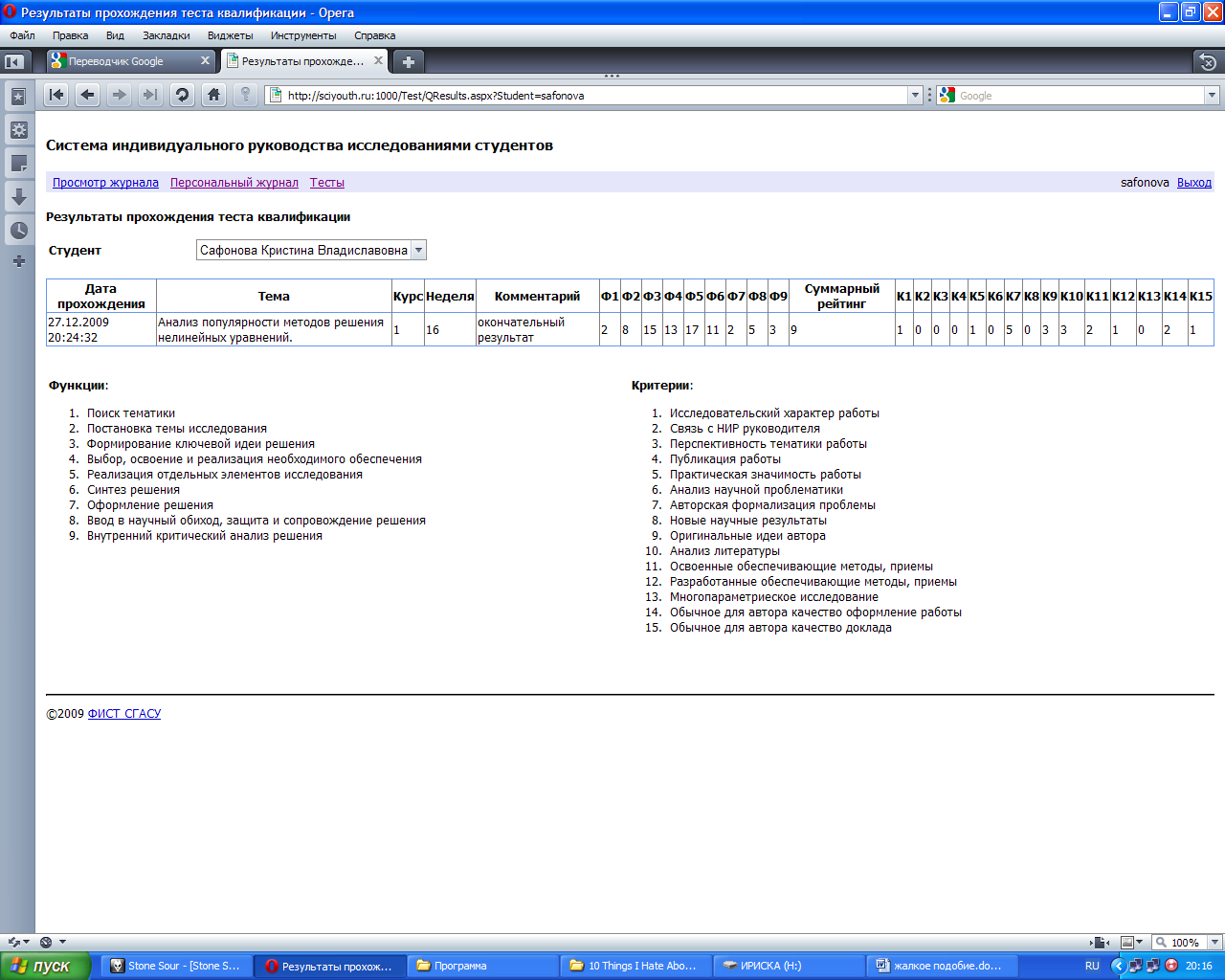
Аннотация

Насколько нам известно, уравнения вида F(x)=0 называют нелинейными уравнениями. Мной были рассмотрены из целого множества возможных методов их решений всего три: метод касательных (он же метод Ньютона), метод хорд, метод половинного деления.

Метод касательных заключается в проведении касательных к графику функции и нахождении её пересечения с осью абсцисс. Далее из этой точки также проводиться касательная, а потом ещё одна и ещё одна и процесс повторяется до тех пор, пока разность между текущей и следующей точкой не станет меньше требуемой точности.

При методе хорд мы выбираем интервал от a до b, где заведомо существует один корень. Далее, мы проводим через точки (a, f(a)) и (b, f(b)) хорду. Эта хорда пересекает ось абсцисс в точке c. Если f(a)*f(b) < 0, то мы заменяем b на c, иначе на c заменяем a. Данный процесс продолжается до тех пор, пока разность между a и b не станет меньше требуемой точности или значение функции в точке c станет меньше требуемой точности.

При методе половинного деления мы выбираем интервал от a до b, где заведомо существует один корень. Далее, мы делим отрезок [a, b] пополам, получая точку c. Если f(a)*f(b) < 0, то мы заменяем b на c, иначе на c заменяем a. Данный процесс продолжается до тех пор, пока разность между a и b не станет меньше требуемой точности.

При рассмотрении каждого метода я продемонстрировала их использование на практике для решения конкретных уравнений. Также были показаны графики, которые отображают начало хода решения нелинейного уравнения.

Все три метода были реализованы в программе в среде Delphi 7. Созданная мной программа позволяет решить уравнение вида a₁x³+a₂x²+a₃x+a₄=0 с заданной точностью, выдавая в результате найденное решение и количество итераций цикла, которое потребовалось для его нахождения. Полученные данные позволили мне сравнить действенность и практическую пользу данных методов.

В конце работы были сделаны диаграммы, позволяющие нам наглядно увидеть и оценить возможности методов.

Введение

Уравнение типа F(x)=0 или x=f(x) называется нелинейным. Решить уравнение это значит найти такое x, при котором уравнение превращается в тождество. В общем случае уравнение может иметь 0; 1; 2;...∞ корней. Рассмотренные ниже численные методы решения нелинейных уравнений позволяют находить один корень на заданном интервале [a,b]. При этом на интервале должен существовать только один корень. Рассмотрим несколько методов решения нелинейных уравнений.

Математическая модель

Метод касательных

Задаются начальное значение аргумента

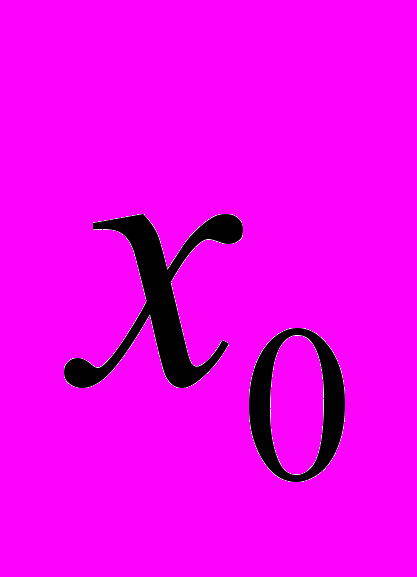и точность

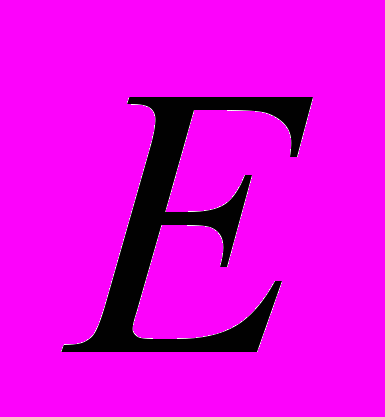. Затем в точке (

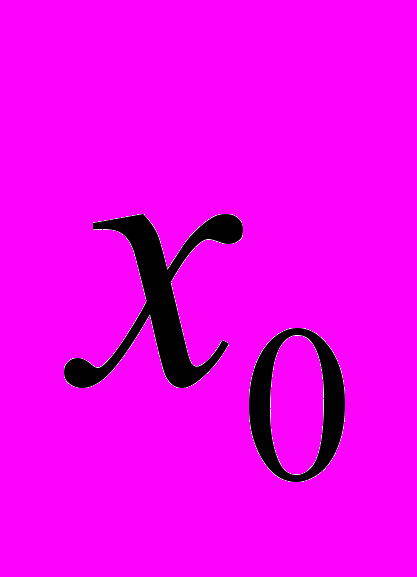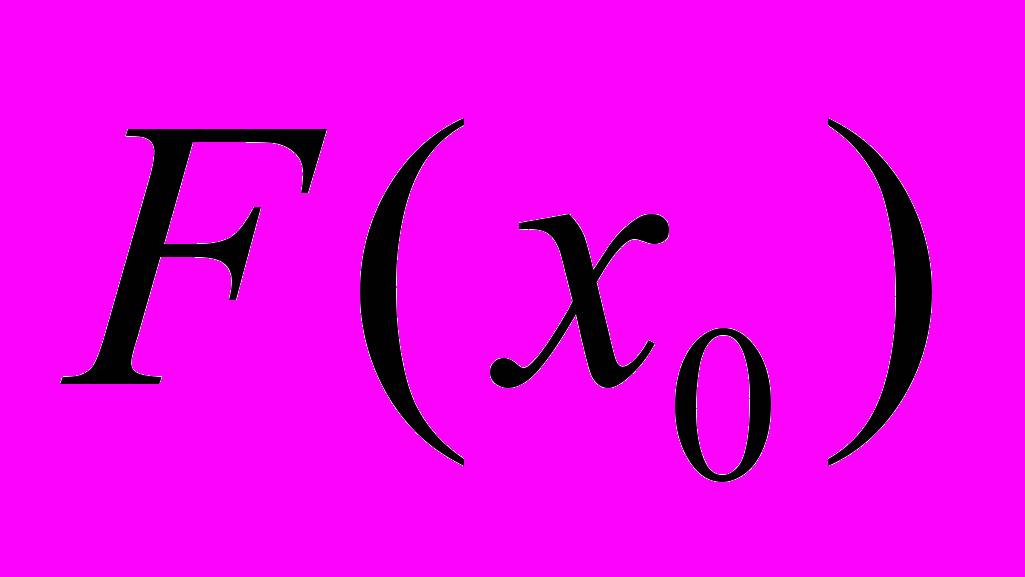) проводим касательную к графику

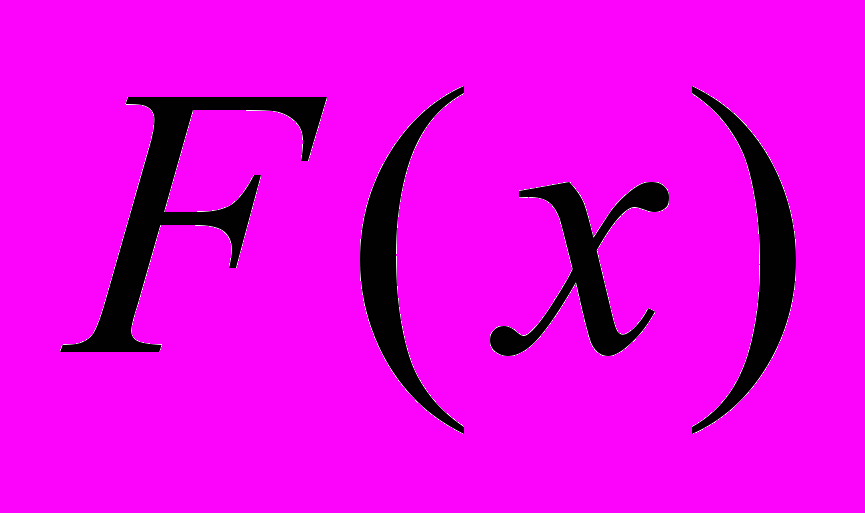и определяем точку пересечения касательной с осью абсцисс

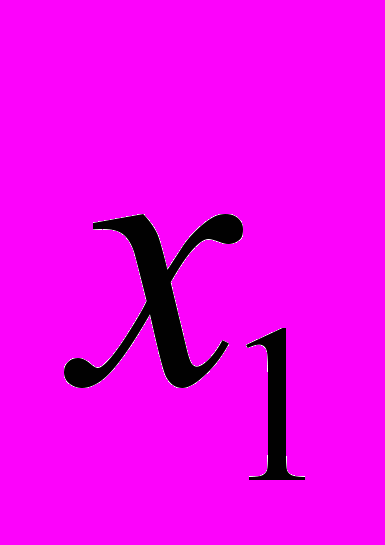. В точке (

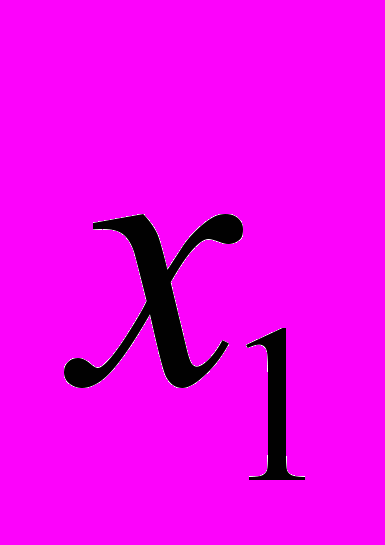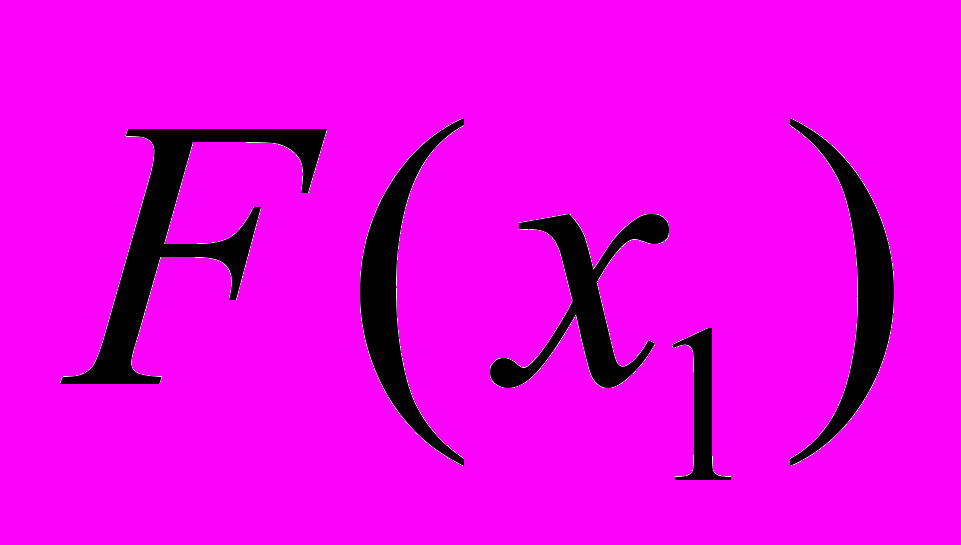) снова строим касательную, находим следующее приближение искомого решения

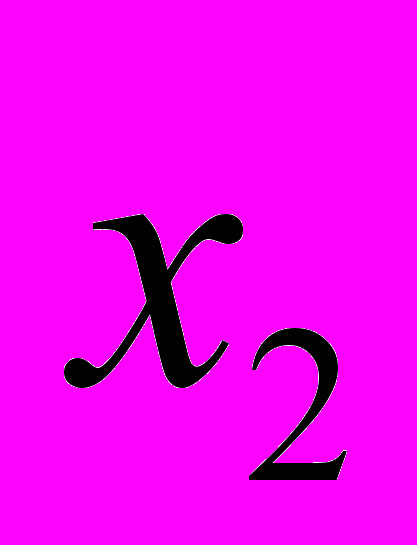и т.д. Указанную процедуру повторяем пока:

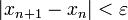или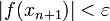

Для определения точки пересечения (n+1) касательной с осью абсцисс воспользуемся следующей формулой:

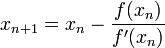
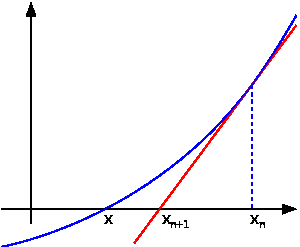
Условие сходимости метода касательных F(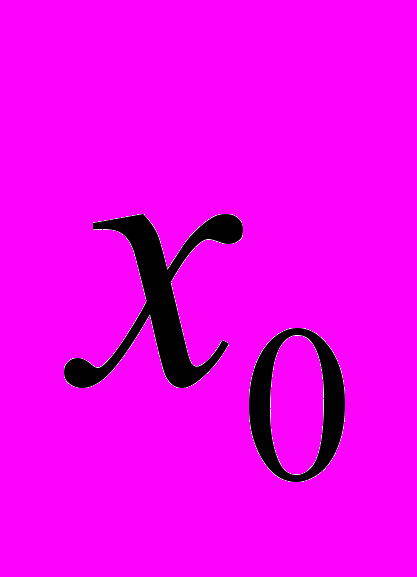)∙F''(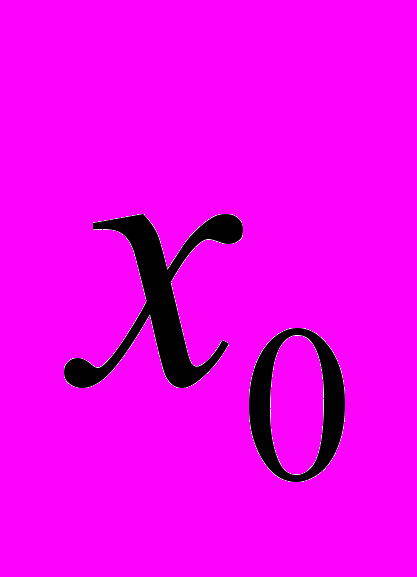)>0.

Пример

Рассмотрим задачу о нахождении положительных x, для которых cosx = x³. Эта задача может быть представлена как задача нахождения нуля функции f(x) = cosx − x³. Имеем выражение для производной f'(x) = − sinx − 3x². Так как cos(x)<=1 для всех x и x³ > 1 для x > 1, очевидно, что решение лежит между 0 и 1. Возьмём в качестве начального приближения значение x₀ = 0,5, тогда:

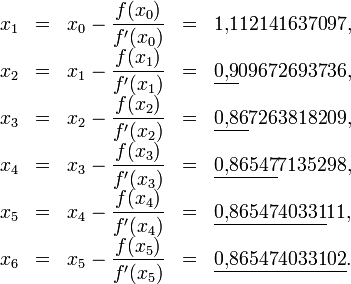
Подчёркиванием отмечены верные значащие цифры. Видно, что их количество от шага к шагу растёт (приблизительно удваиваясь с каждым шагом): от 1 к 2, от 2 к 5, от 5 к 10, иллюстрируя квадратичную скорость сходимости.

Метод хорд

Задаются интервал [a,b], на котором существует только одно решение, и точность ε. Затем через две точки с координатами (a,F(a)) и (b,F(b)) проводим отрезок прямой линии (хорду) и определяем точку пересечения этой линии с осью абсцисс (точка c). Если при этом F(a)∙F(c)<0, то правую границу интервала переносим в точку с (b=c). Если указанное условие не выполняется, то в точку c переносится левая граница интервала (а=с). Поиск решения прекращается при достижении заданной точности |F(c)|< ε. Для определения точки пересечения хорды с осью абсцисс воспользуемся следующей формулой:

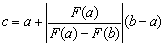
Пример

Решим уравнение x³ − 18 * x − 83 = 0 методом хорд. Зададимся точностью ε=0.001 и возьмём в качестве начальных приближений x₀ и x₁ концы отрезка, на котором отделён корень: x₀= 8 и x₁ = 3.Вычисления ведутся до тех пор, пока не выполнится неравенство

.

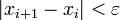Итерационная формула метода хорд имеет вид:

.

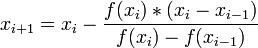По этой формуле последовательно получаем:

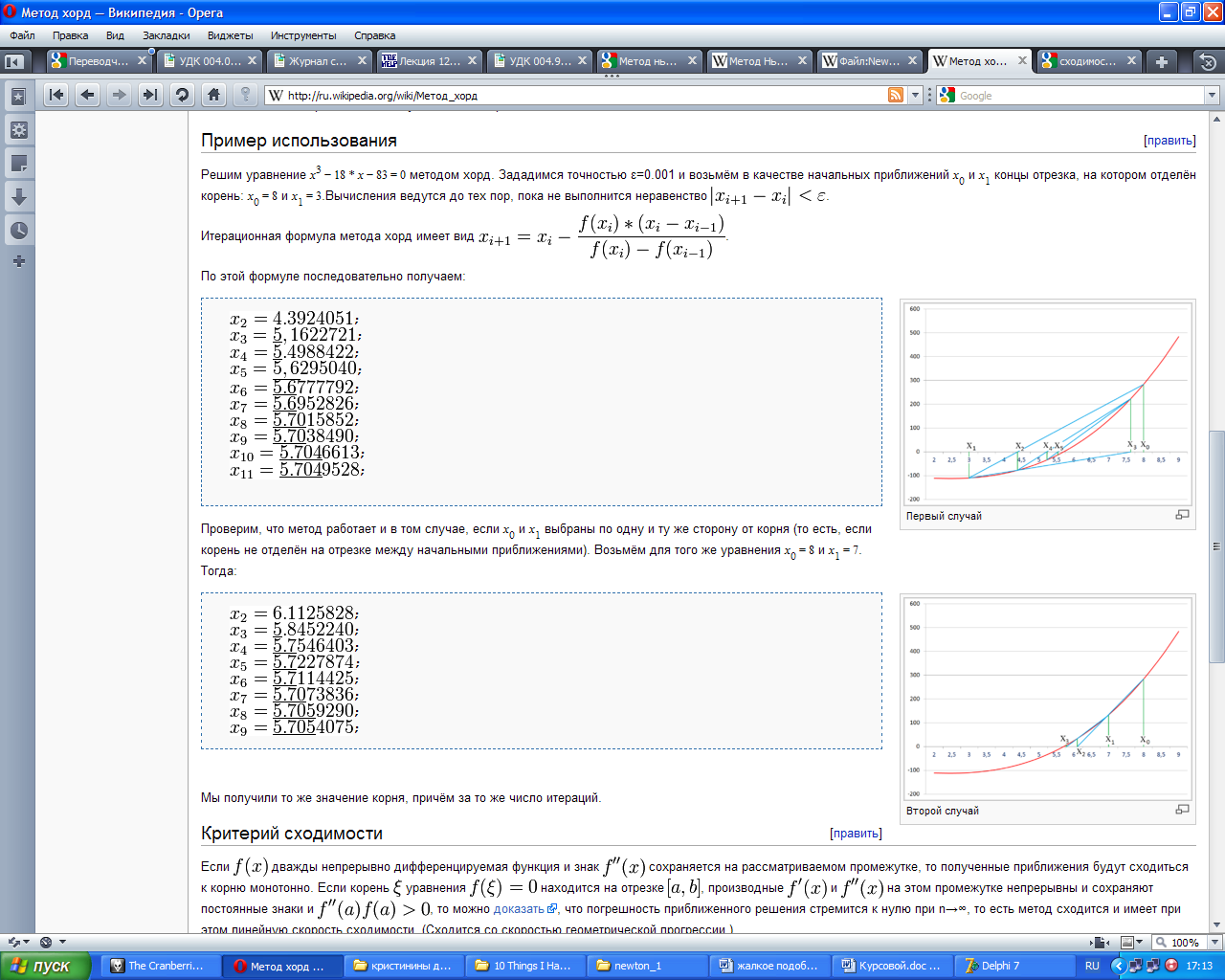
Проверим, что метод работает и в том случае, если x₀ и x₁ выбраны по одну и ту же сторону от корня (то есть, если корень не отделён на отрезке между начальными приближениями). Возьмём для того же уравнения x₀ = 8 и x₁ = 7. Тогда:

Метод половинного деления

Задаются интервал [a,b], на котором существует только одно решение, и желаемая точность ε. Затем определяется середина интервала с=(а+b)/2 и проверяется условие F(a)∙F(c)<0. Если указанное условие выполняется, то правую границу интервала b переносим в среднюю точку с (b=c). Если условие не выполняется, то в среднюю точку переносим левую границу (a=c). Деление отрезка пополам продолжается пока |b-a|>ε.

Реализация плана исследований.

Данные методы решения нелинейных уравнений были реализованы в Delphi в программе, позволяющей решить уравнение вида a₁x³+a₂x²+a₃x+a₄=0.

Метод касательных. Фрагмент кода:

function Metod_1(X0: Real): Real;

var

x1, x2 : Real;

begin

Result := 0;

if (F(X0)*F2(X0) <= 0) Then

begin

Application.MessageBox('Условие сходимости не выполняется! Введите другой X0.', 'Ошибка', MB_ICONERROR);

exit;

end;

x2 := x0;

Repeat

x1 := x2;

x2 := x1 - f(x1)/f1(x1);

Inc(iter);

Until ((abs(x2-x1) <= e) or (abs(f(x2)) <= e));

Result := x2;

end;

Метод хорд. Фрагмент кода:

function Metod_2(a, b: Real): Real;

var

c : Real;

begin

Result := a;

Repeat

c := a + abs(f(a)/(f(a) - f(b)))*(b-a);

if (f(a)*f(b) < 0) Then

begin

b := c;

end else

begin

a := c;

end;

Inc(iter);

Until ((abs(a-b) <= e) or (f(c) <= e));

Result := c;

end;

Метод половинного деления. Фрагмент кода:

function Metod_3(a, b: Real): Real;

var

c : Real;

begin

Result := a;

Repeat

c := (a+b)/2;

if (f(a)*f(b) < 0) Then

begin

b := c;

end else

begin

a := c;

end;

Inc(iter);

Until ((abs(a-b) <= e));

Result := c;

end;

Скриншот работы программы:

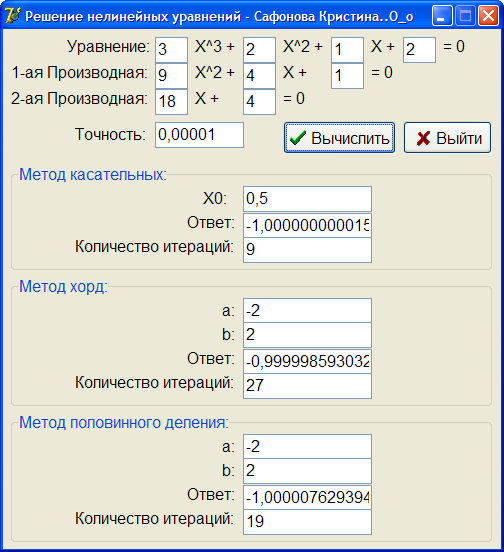
Вывод

В результате работы программы мы получили решения и количество итераций для каждого метода.

Метод		Погрешность	Количество итераций
1.	Метод касательных	0,00000000001	9
2.	Метод хорд	0,000001	27
3.	Метод половинного деления	0,000001	19

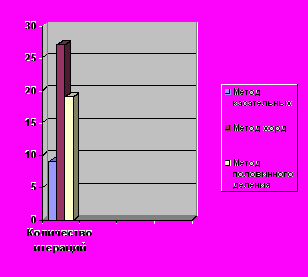
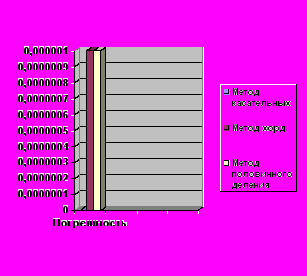
Рис. сравнение результатов

Из полученных значений мы видим, что за самое наименьшее число шагов и с большей точностью найти решение нелинейного уравнения позволяет метод касательных. Метод половинного деления, как и метод хорд, обладают большей погрешностью и достигают результата за большее количество шагов.

Библиографический список

1. Технология научных исследований: Методические указания к выполнению лабораторных работ / С. А. Пиявский; Самарский государственный архитектурно-строительный ун-т./ Самара, 2006. – 40 с.

2. Метод Ньютона – Википедия // Режим доступа: dia.org/wiki/Метод_Ньютона

3. Метод половинного деления // od.ru/div/

4. Методы решения НЛУ– www.toehelp.ru [Электронный ресурс] // Режим доступа: lp.ru/theory/informat/lecture12.php.

Blog

Расшифровка : Наука в целом (информационные технологии 004)

Содержание