Лекция № Тема 1: Системы линейных алгебраических уравнений. Метод Гаусса решения систем уравнений. Неопределенные системы уравнений

Вид материала

Лекция

Подобный материал:

• Лекция №1. Тема 1: Системы линейных алгебраических уравнений. Метод Гаусса решения, 47.04kb.
• Программа решения системы линейных уравнений по методу Гаусса 7 2 Программа решения, 230.48kb.
• Название читаемого курса, 134.62kb.
• Вопросы к экзамену 1 семестр, 56.89kb.
• Тема: «решение систем линейных алгебраических уравнений методом гаусса», 52.92kb.
• Элемен ты линейной и векторной алгебры, 26.56kb.
• Kirgizistan-tüRKİye manas üNİversitesi ders biLGİ formu, 113.45kb.
• Контрольная работа по линейной алгебре и аналитической геометрии «Системы линейных, 383.4kb.
• Решение систем нелинейных уравнений, 119.58kb.
• Метод касательных гиперплоскостей для решения систем нелинейных алгебраических уравнений, 25.48kb.

Лекция № 2.

Тема 1: Системы линейных алгебраических уравнений. Метод Гаусса решения систем уравнений. Неопределенные системы уравнений.


Задача 2.1. Решить систему уравнений:


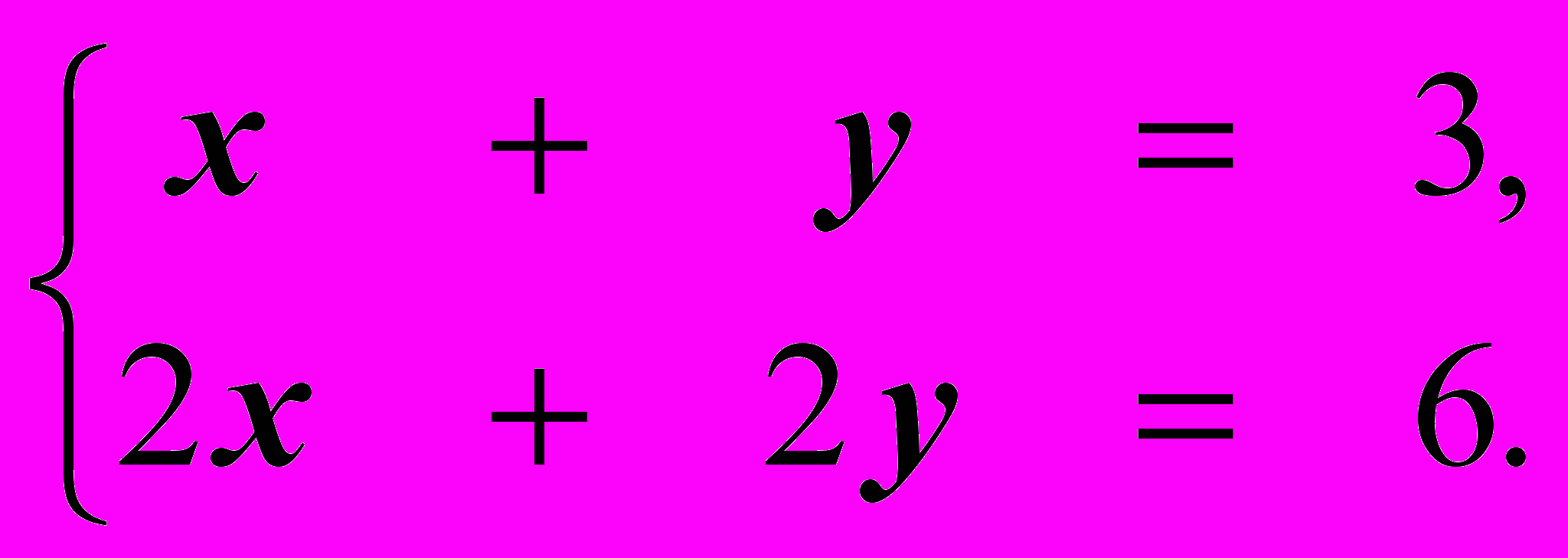
(1)


Решение:

Попробуем, как и раньше, производить элементарные преобразования над системой уравнений, приводя её к более простому виду. Вычтем из 2-го уравнения 1-е, умноженное на 2, и получим систему (1а):



Так как второе уравнение полученной системы представляет собой тождество (равенство, верное при любых значениях переменных x и y), то система (1а) эквивалентна системе (1б), состоящей из одного уравнения:



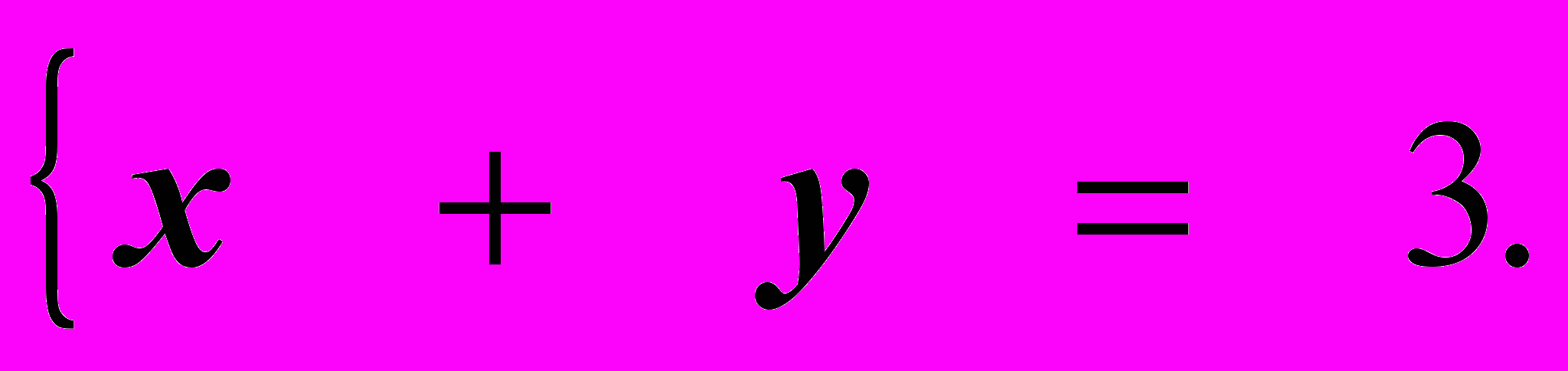
И сколько же решений (т.е. упорядоченных пар чисел (x, y)) у этой, с позволения сказать, системы? Очевидно, немало. Например, решениями этой системы являются пары чисел: (1; 2), (0; 3), (-8; 11), (2,5; 0,5) и т.д.

Правильным будет заключение о том, что данная система имеет бесконечное множество решений, т.е. по определению является ___________________ (вспомните и напишите сами). А решить систему означает указать множество всех (!) её решений. И как же это сделать?

Перенесем какую-нибудь одну из переменных, например, переменную y, в правую часть уравнения и получим следующее уравнение:

x = 3 - y.

Легко видеть, что если переменной y присвоить какое-нибудь (произвольное) числовое значение (к примеру, y = 2), то переменная x автоматически примет одно вполне определенное значение, равное 3 - y (при y = 2 получим x = 3 - 2 = 1). Таким образом, решением системы будет любая пара чисел вида

(x = 3 - y, y).

Можно оставить ответ и в таком виде, а можно и в более стандартном (общепринятом): (3 - t, t), где t - любое действительное число (t  R). Итак,

Ответ: (3 - t, t), t  R.

Мрак, да?


Задача 2.2. Решить систему уравнений:


(2)


Решение: Запишем расширенную матрицу системы и элементарными преобразованиями над ее строками приведем основную матрицу системы к ступенчатому виду (прямой ход метода Гаусса):




Запишем систему уравнений с полученной расширенной матрицей:



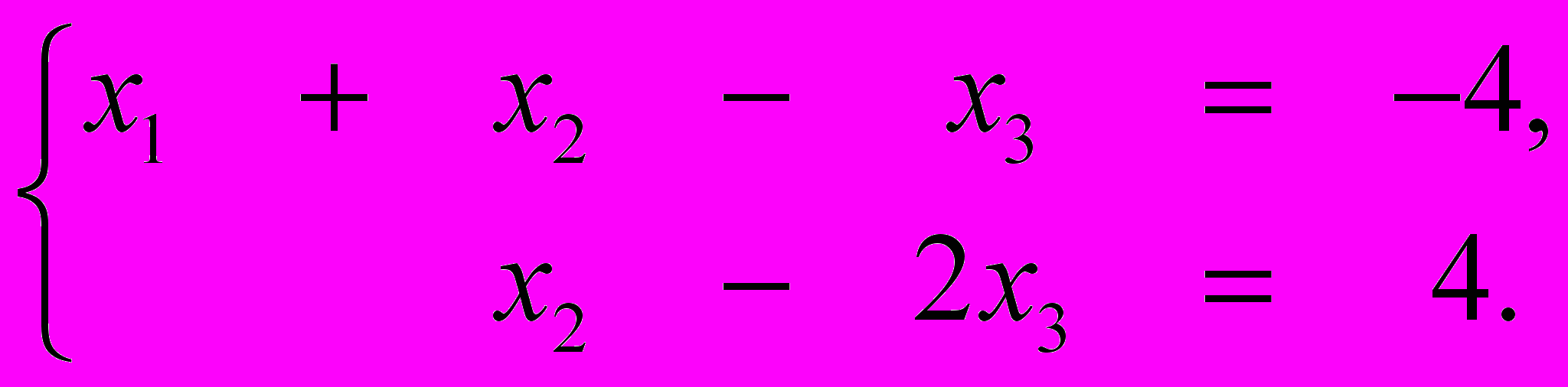
(Кстати, а почему уравнений не три, а два? Напишите здесь: ...............................................

.....................................................................................................................................................).

Как и при решении системы (1), перенесем какую-нибудь одну переменную, например, переменную x₃, вправо и получим следующую систему:



Подставляя выражение для x₂ из второго уравнения в первое, получим систему:



Уже можно догадаться, что решением этой (а значит, и исходной) системы является любая тройка чисел вида

(x₁ = - x­₃ - 8, x₂ = 2x₃ + 4, x₃).

Но более стандартным выглядит

Ответ: (- t - 8, 2t + 4, t), t  R.

Записанный в таком виде ответ представляет собой общее решение системы (2).

Переменная будет x­₃ называться свободной, а переменные x­₁ и x­₂ - главными.


Теперь немного теории:


Прямым ходом метода Гаусса (при решении системы линейных алгебраических уравнений) будем называть такую последовательность элементарных преобразований, производимых со строками расширенной матрицы системы, которая приводит основную матрицу системы к ступенчатому виду.

Общим решением системы называется множество всех ее решений, записанное в виде формулы, в которой одни переменные (называемые главными переменными), выражаются через другие (называемые свободными переменными). Например, общее решение системы может быть записано в таком виде:





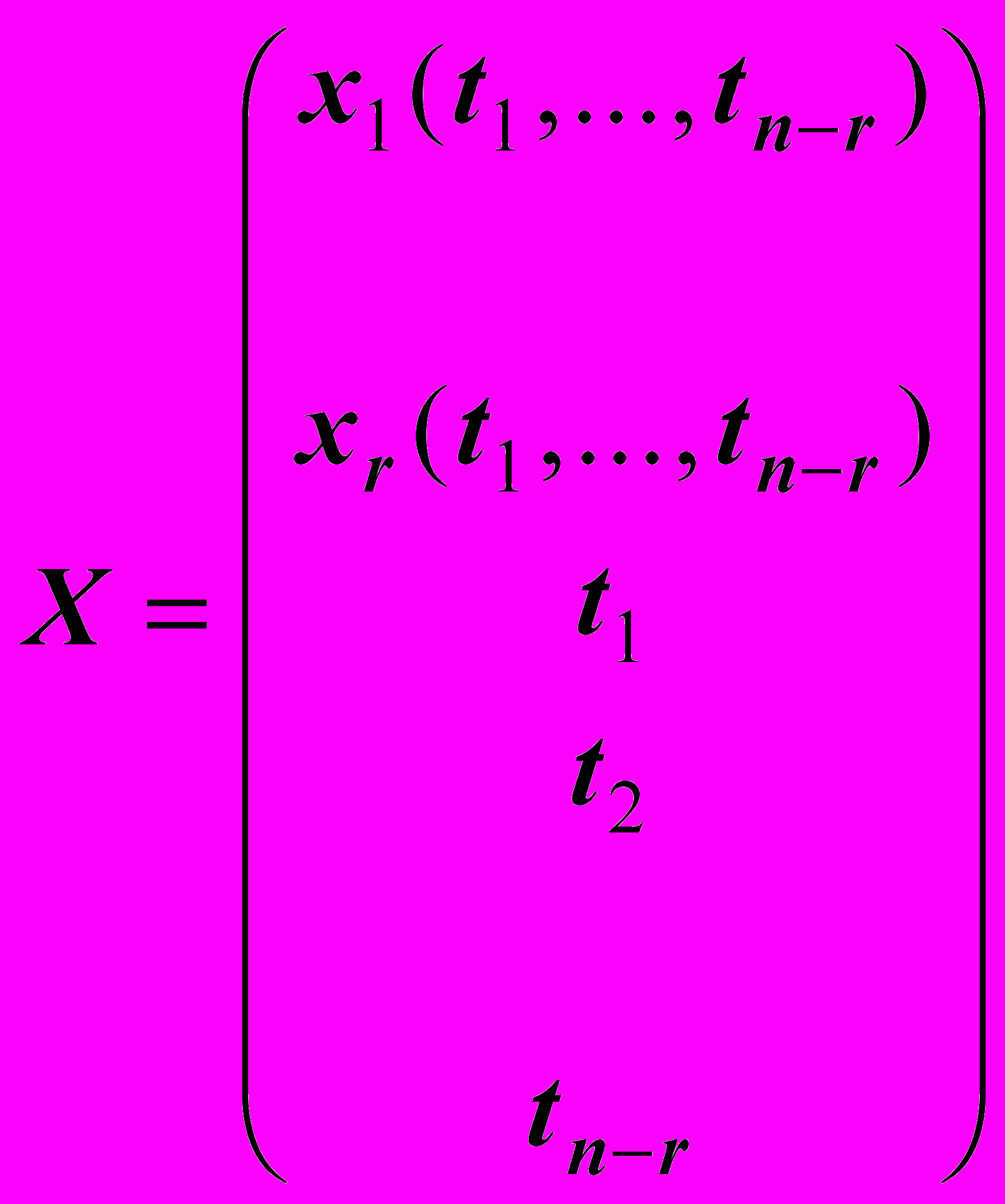
В этой записи x₁, x₂, ..., x_r (главные переменные) выражаются через x_r+1, ..., x_n (свободные переменные), а t₁, ..., t_n-r - набор произвольных n-r чисел. Каждому фиксированному набору числовых значений t₁, ..., t_n-r свободных переменных (x_r+1 = t₁, ..., x_n = t_n-r) соответствует единственное решение системы.

___________________________________________________________________________


Задача 2.3. Решить систему уравнений (3):



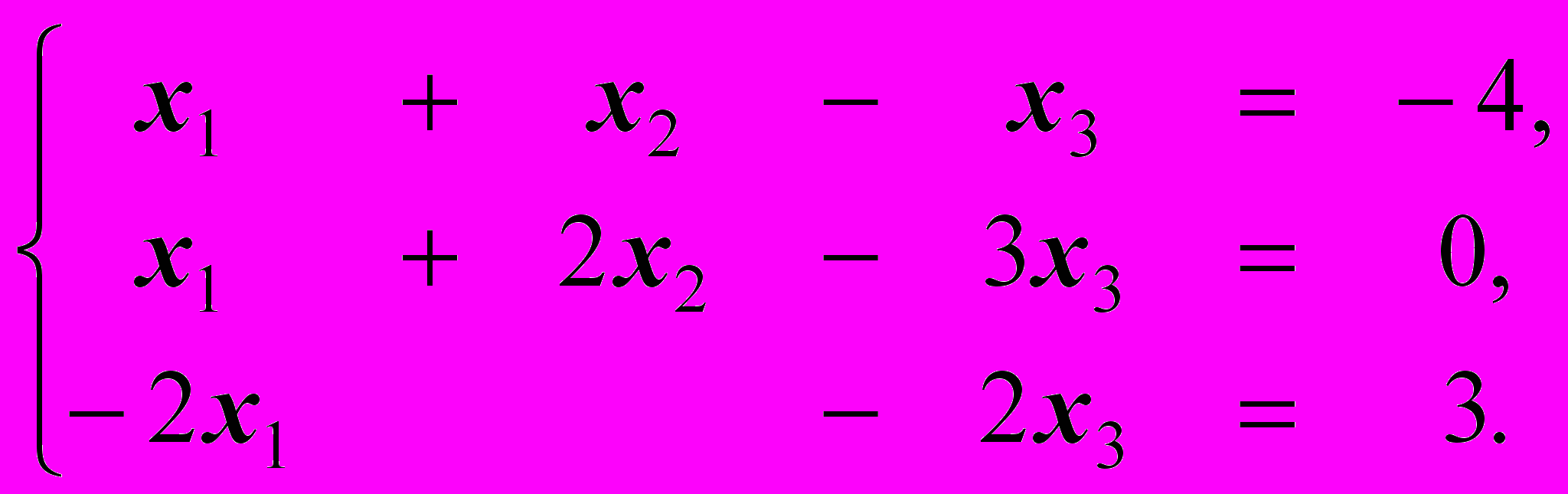
Не кажется ли вам, что мы подобную систему уже решали?

Решение: Запишем расширенную матрицу системы и элементарными преобразованиями над ее строками приведем основную матрицу системы к ступенчатому виду (прямой ход метода Гаусса):



Запишем систему с полученной расширенной матрицей:



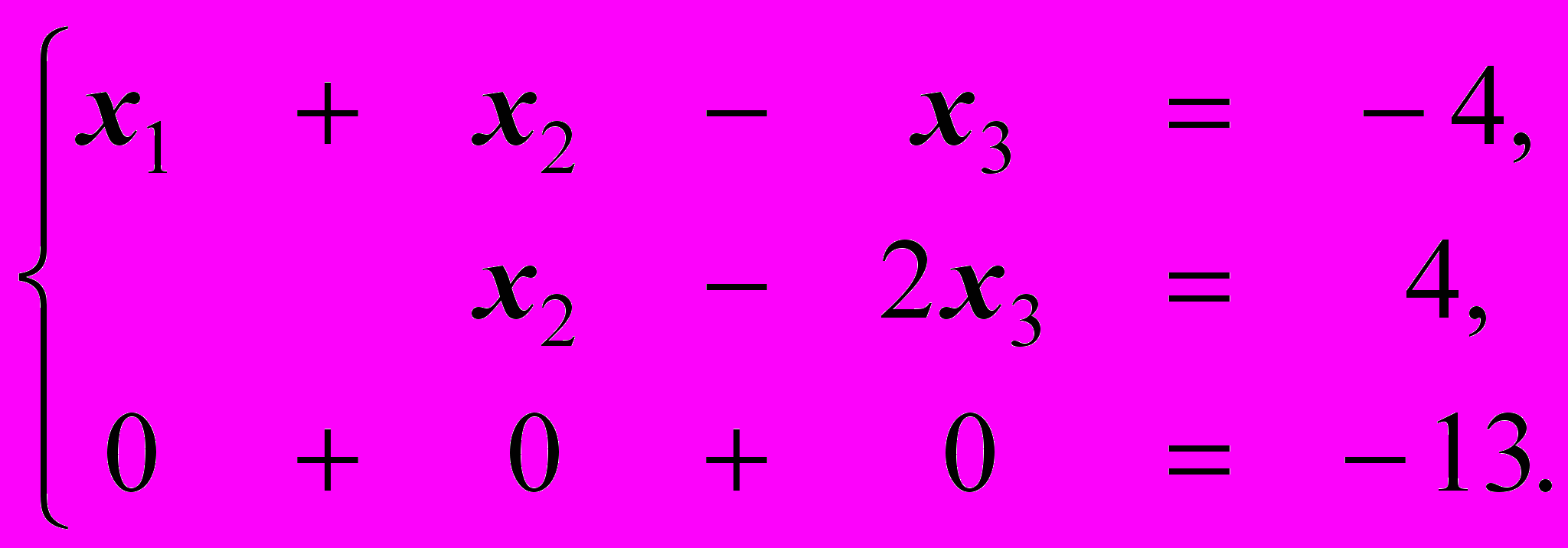
Нетрудно видеть, что полученная система несовместна. Кстати, это можно было бы понять сразу - по виду расширенной матрицы, не восстанавливая соответствующую систему.

Опять немного теории:

Исследование систем линейных алгебраических уравнений.


Пусть после применения прямого хода метода Гаусса расширенная матрица некоторой системы приведена к такому виду, что основная матрица полученной системы будет ступенчатой:

0	...	0	a'1k1						...		a'1n	b'1
0	...		0	...	0	a'2k2			...		a'2n	b'2
	-		-		-		-		-		-	...
0			...			0	...	0	a'rkr	...	a'rn	b'r
0			...			0	...		0	...	0	b'r+1
	-		-		-		-		-		-	...
0			...						0	...	0	b'm

О

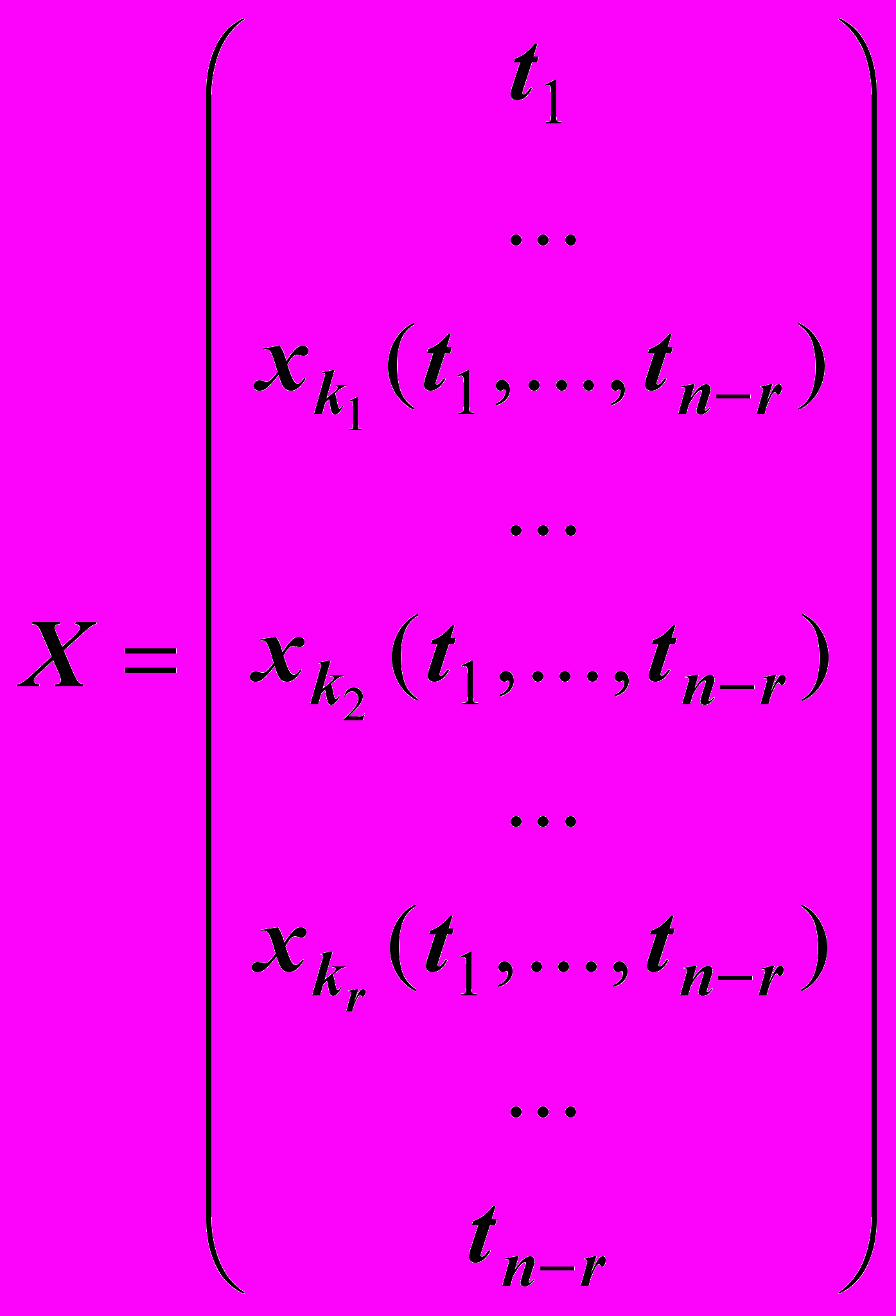
чевидно, что если хотя бы одно из чисел b'_r+1, ..., b'_m (например, число b'_k) окажется не равным 0, то соответствующее уравнение будет таким: 0 = b'_k  0, и система будет несовместна.

Если же b'_r+1 = ...= b'_m = 0, то система будет совместна, переменные x_k1, x_k2 , ..., x_kr будут главными, а остальные переменные - свободными. В этом случае общее решение системы будет записываться следующим образом:

П
ри этом каждому фиксированному набору числовых значений t₁, ..., t_n-r свободных переменных соответствует единственное решение системы.