Контрольная работа по линейной алгебре и аналитической геометрии «Системы линейных уравнений»
| Вид материала | Контрольная работа |
- Контрольная работа по курсу «Линейной алгебры и математического программирования», 99.84kb.
- Системы линейных уравнений, 63.47kb.
- Тематика курсовых работ по линейной алгебре Матрицы и определители: реализация основных, 8.06kb.
- Контрольная работа по алгебре «Правила вычисления производных» Контрольная работа, 65.69kb.
- Решение линейных уравнений Цель урока, 126.51kb.
- Программа решения системы линейных уравнений по методу Гаусса 7 2 Программа решения, 230.48kb.
- Алгоритм решения системы n линейных уравнений методом Гаусса- зейделя представлен, 111.8kb.
- Вопросы к экзамену 1 семестр, 56.89kb.
- Элемен ты линейной и векторной алгебры, 26.56kb.
- 1. Матрица и расширенная матрица системы. Элементарные преобразования матриц. Решение, 8.16kb.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 1
Алифанов
Дана матрица A:
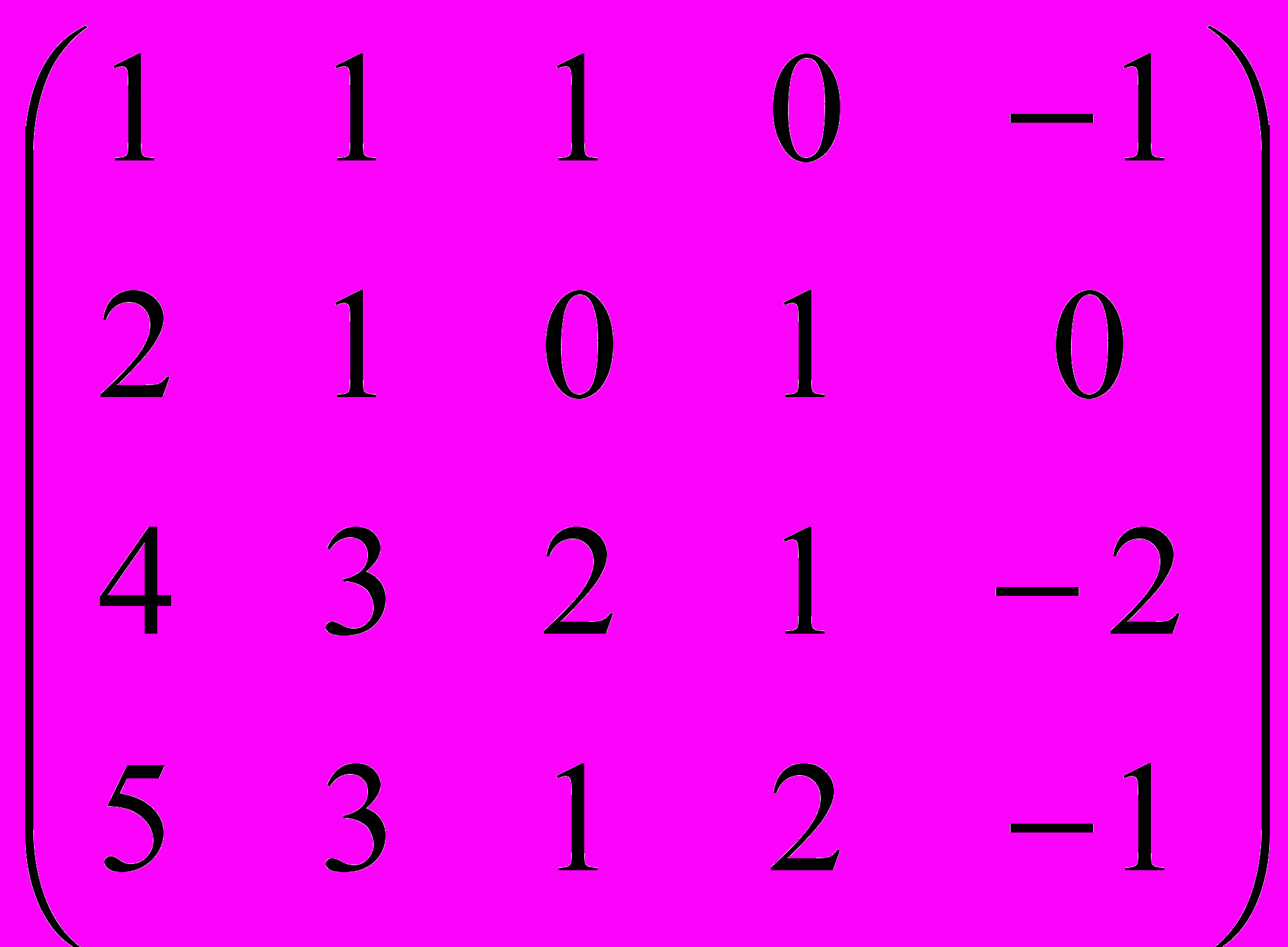 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 2
Деркач
Дана матрица A:
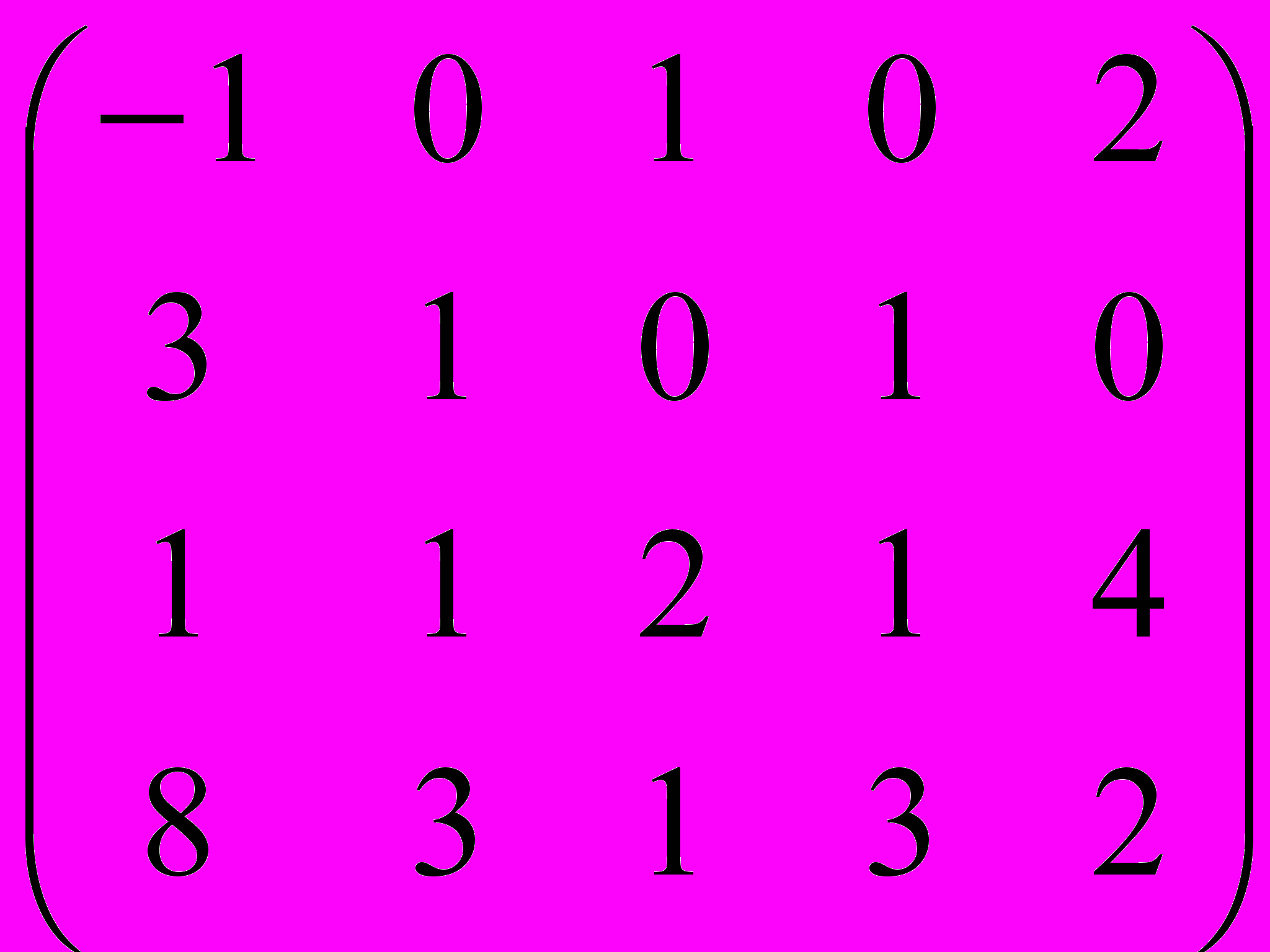 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 3
Дерюгин
Дана матрица A:
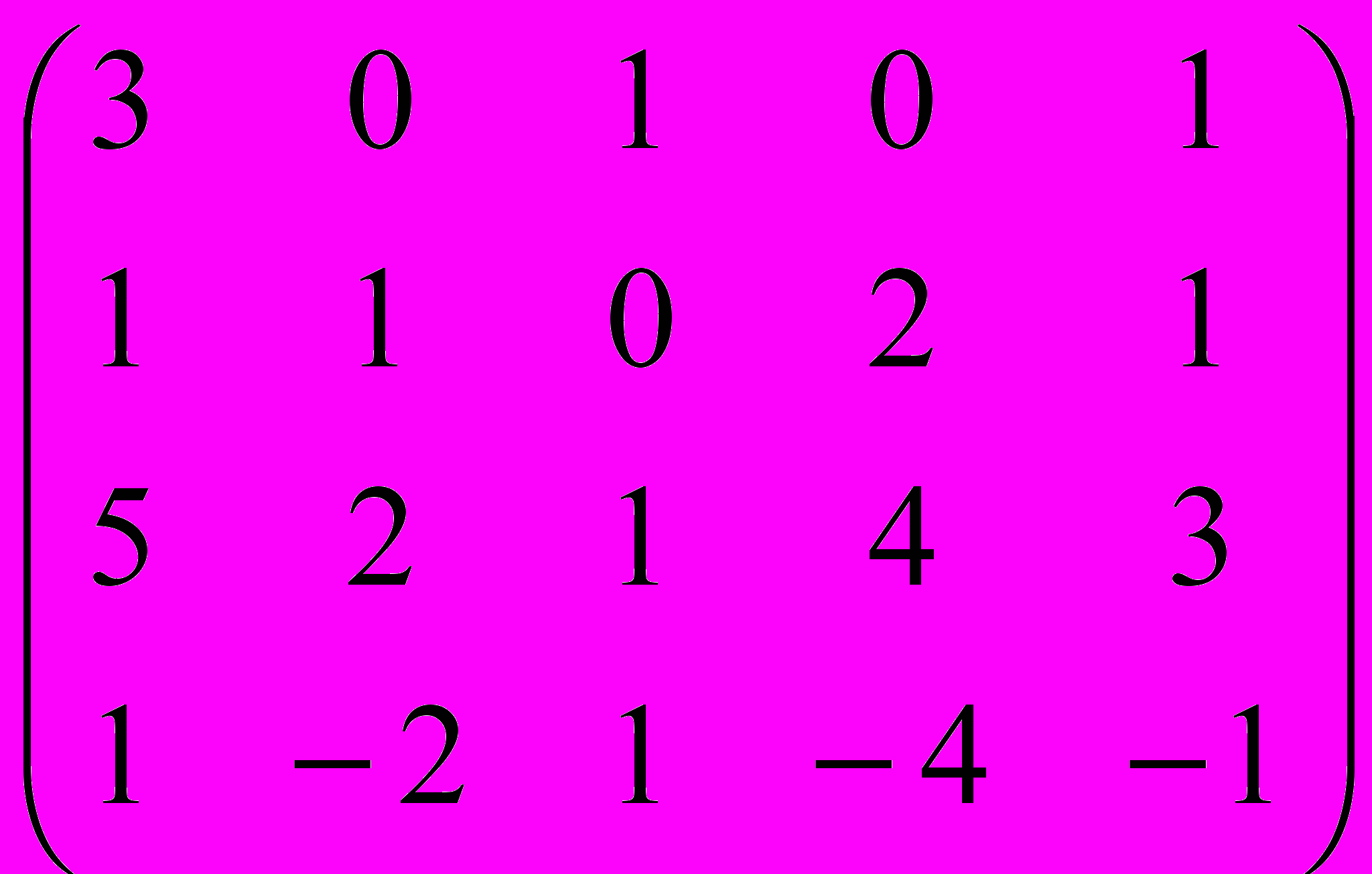 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 4
Диденко
Дана матрица A:
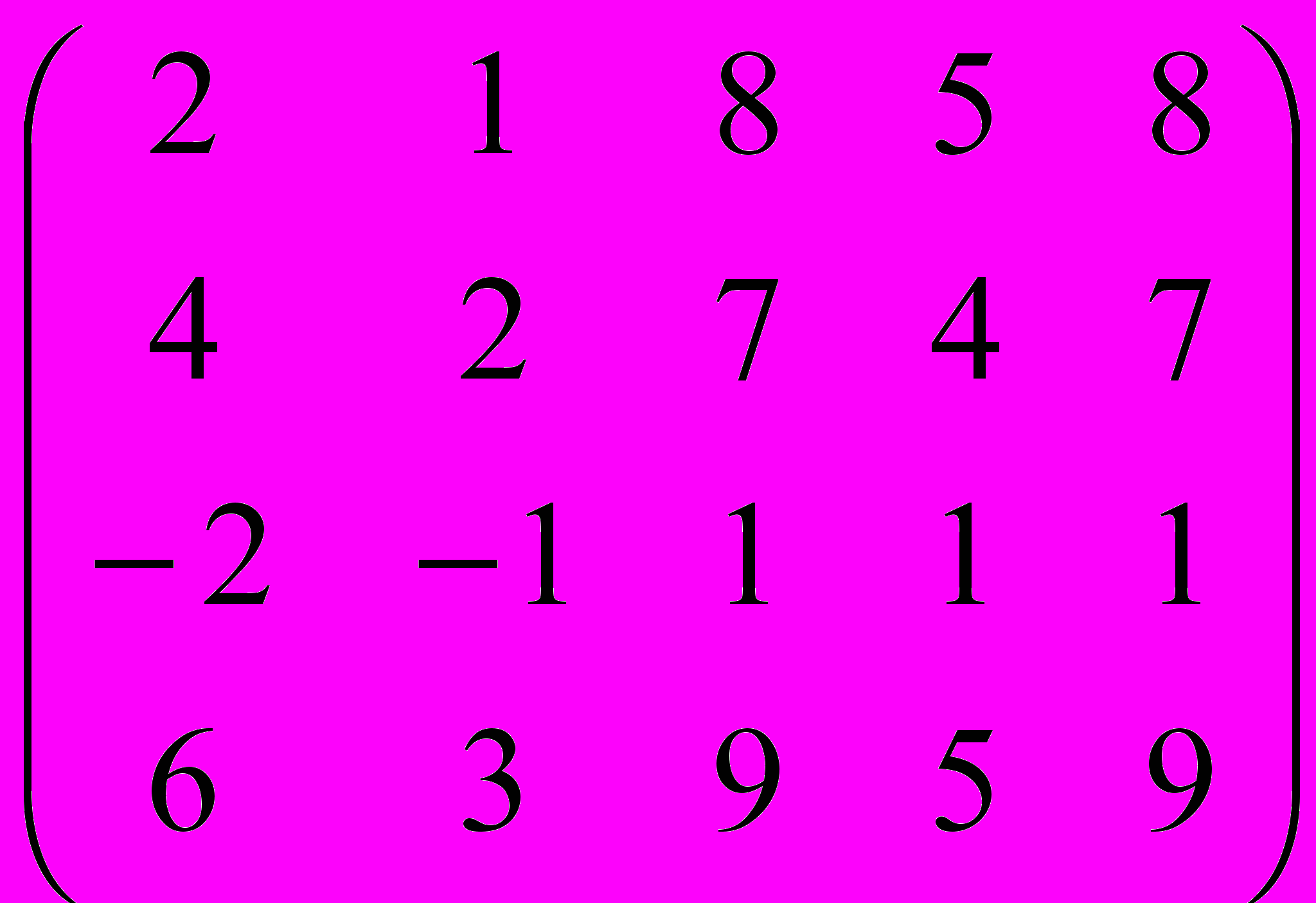 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 5
Золотых
Дана матрица A:
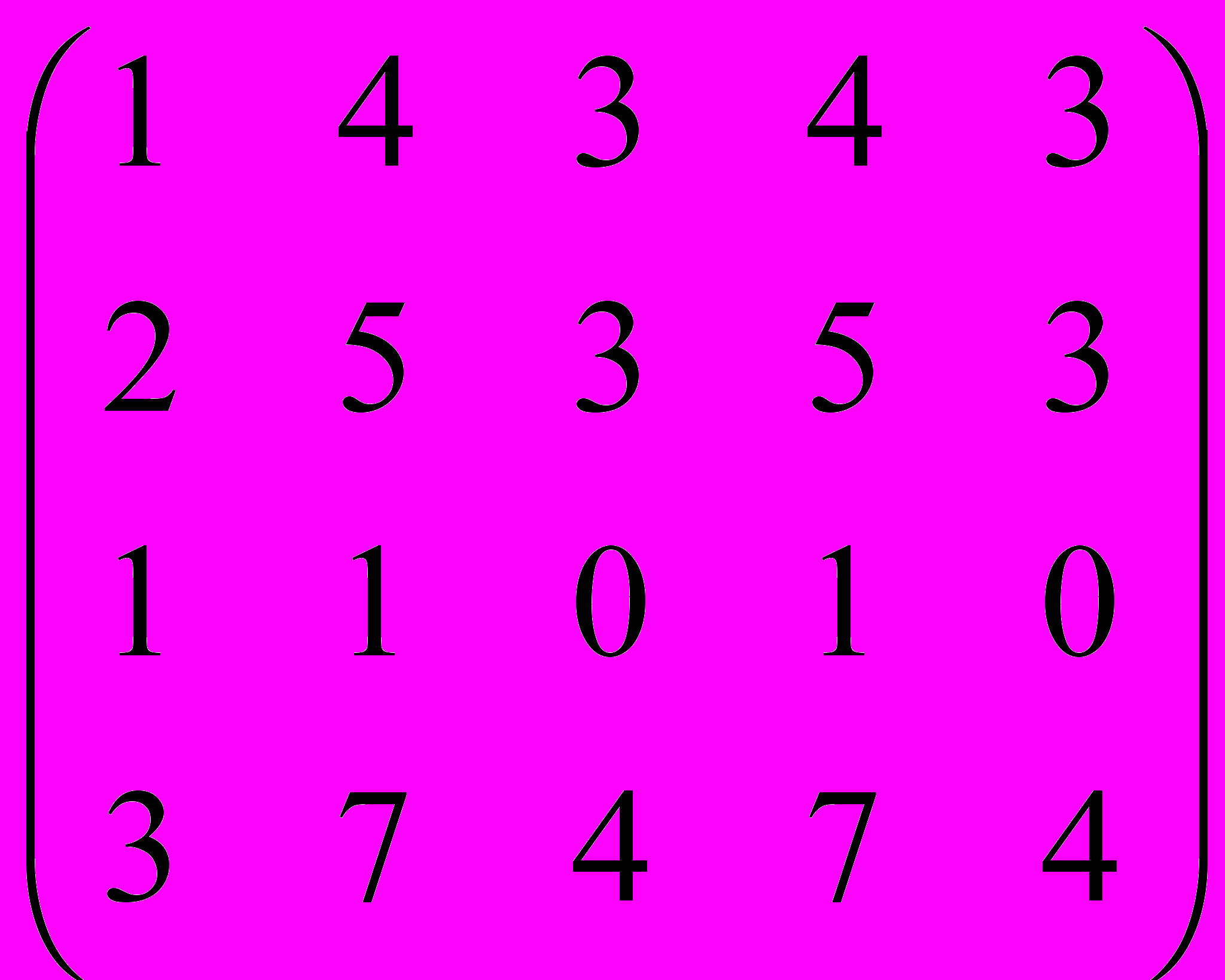 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 6
Кнутова
Дана матрица A:
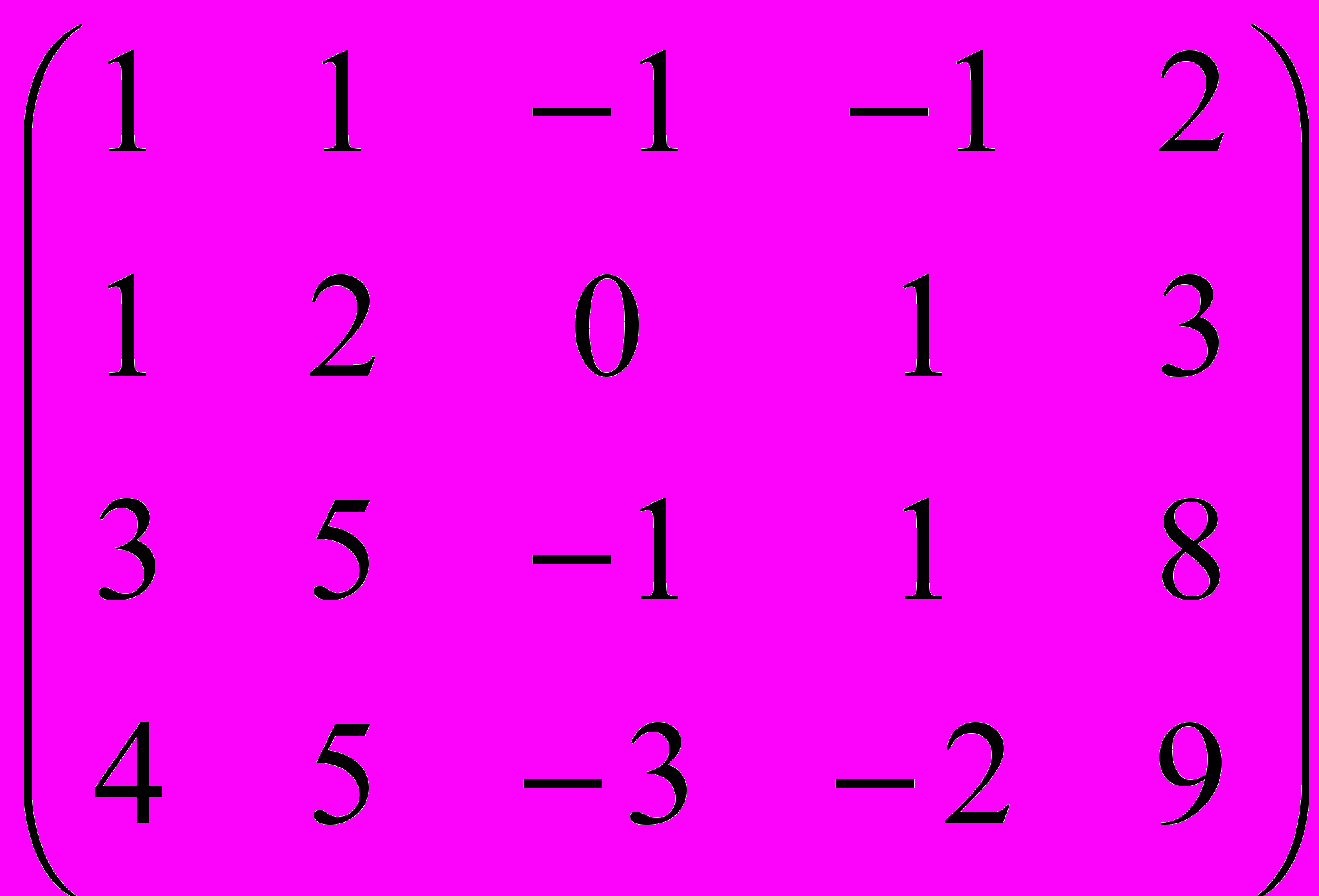 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 7
Ковалевский
Дана матрица A:
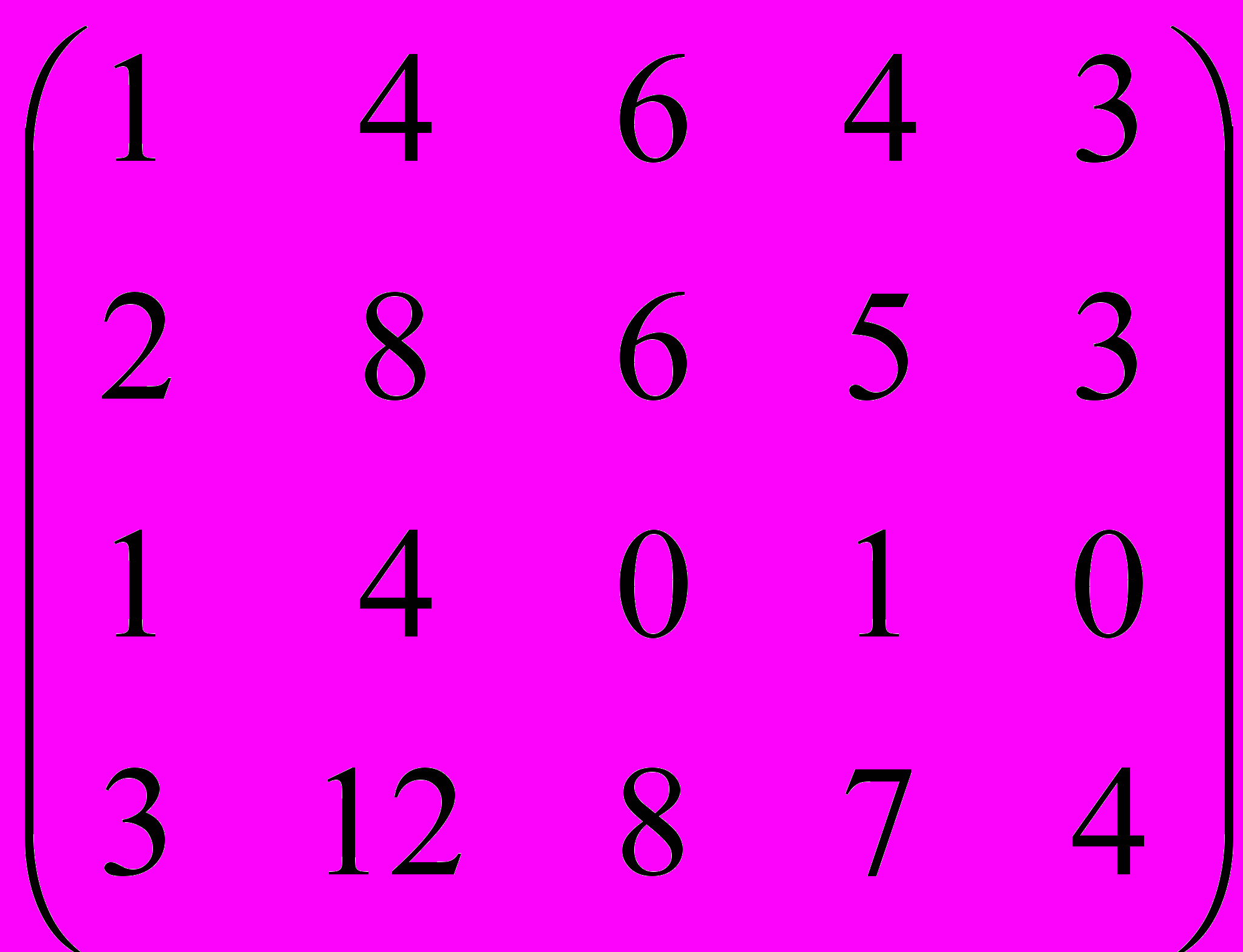 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 8
Кондратьева
Дана матрица A:
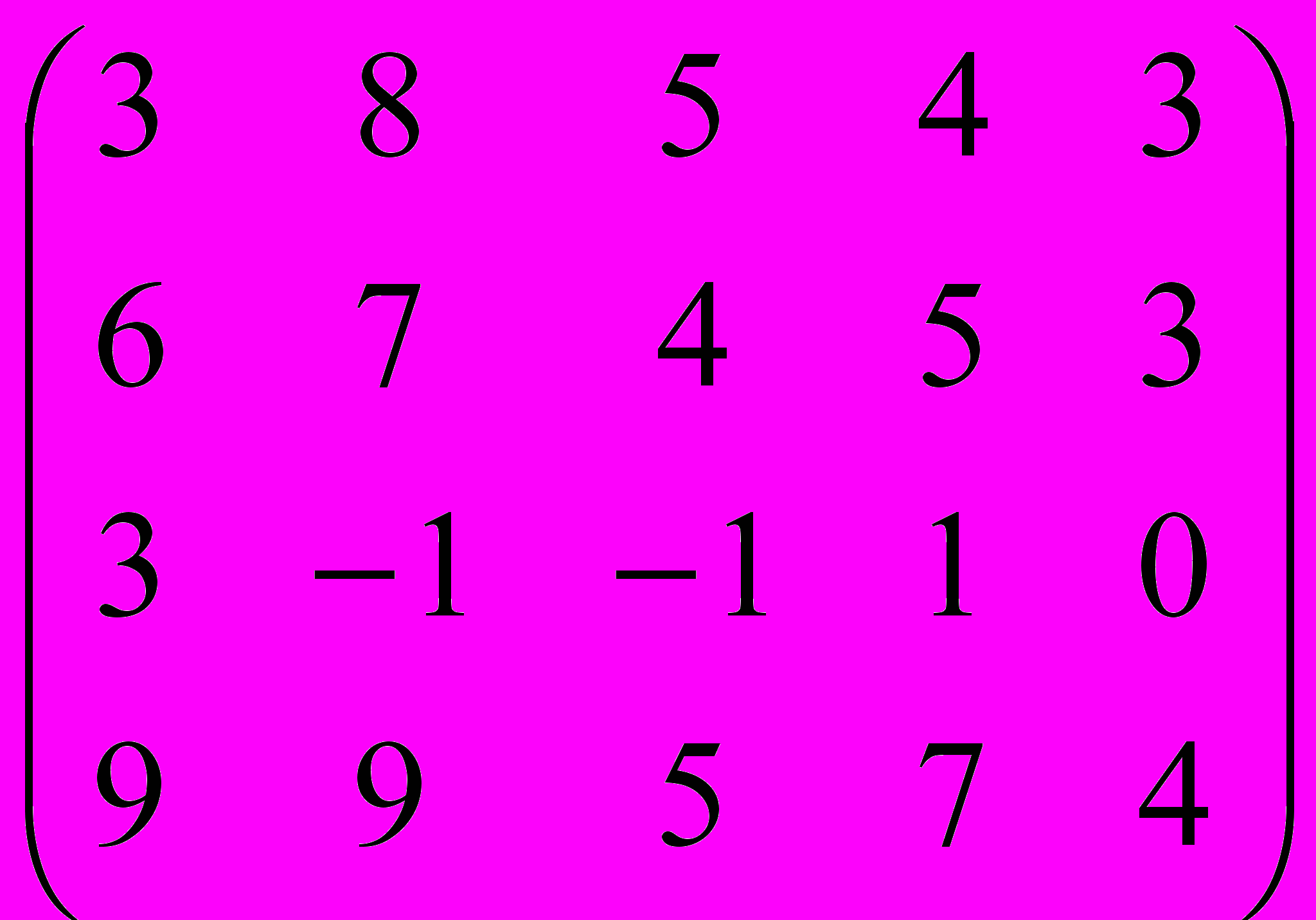 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 9
Лаврентьев
Дана матрица A:
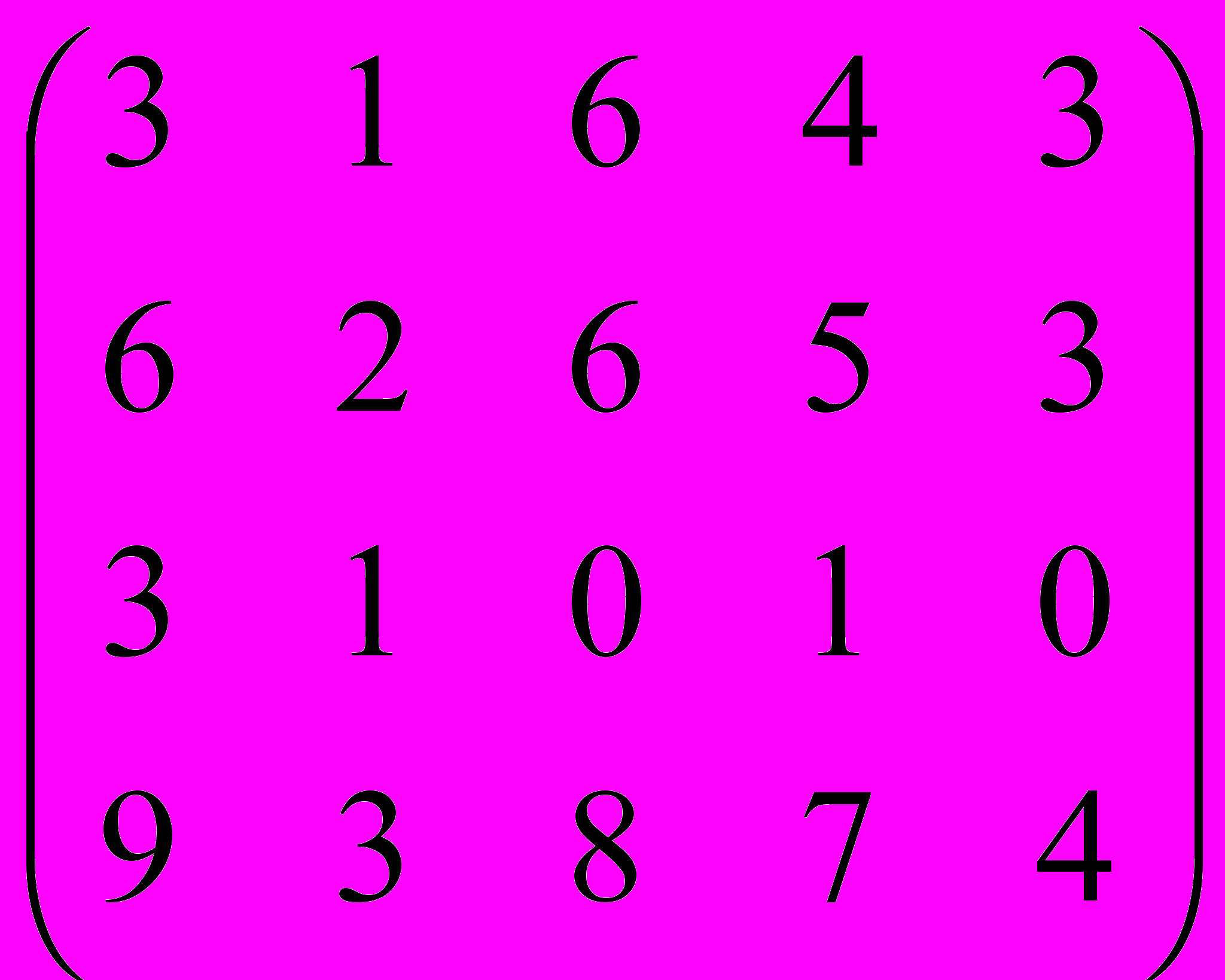 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 10
Никифорова
Дана матрица A:
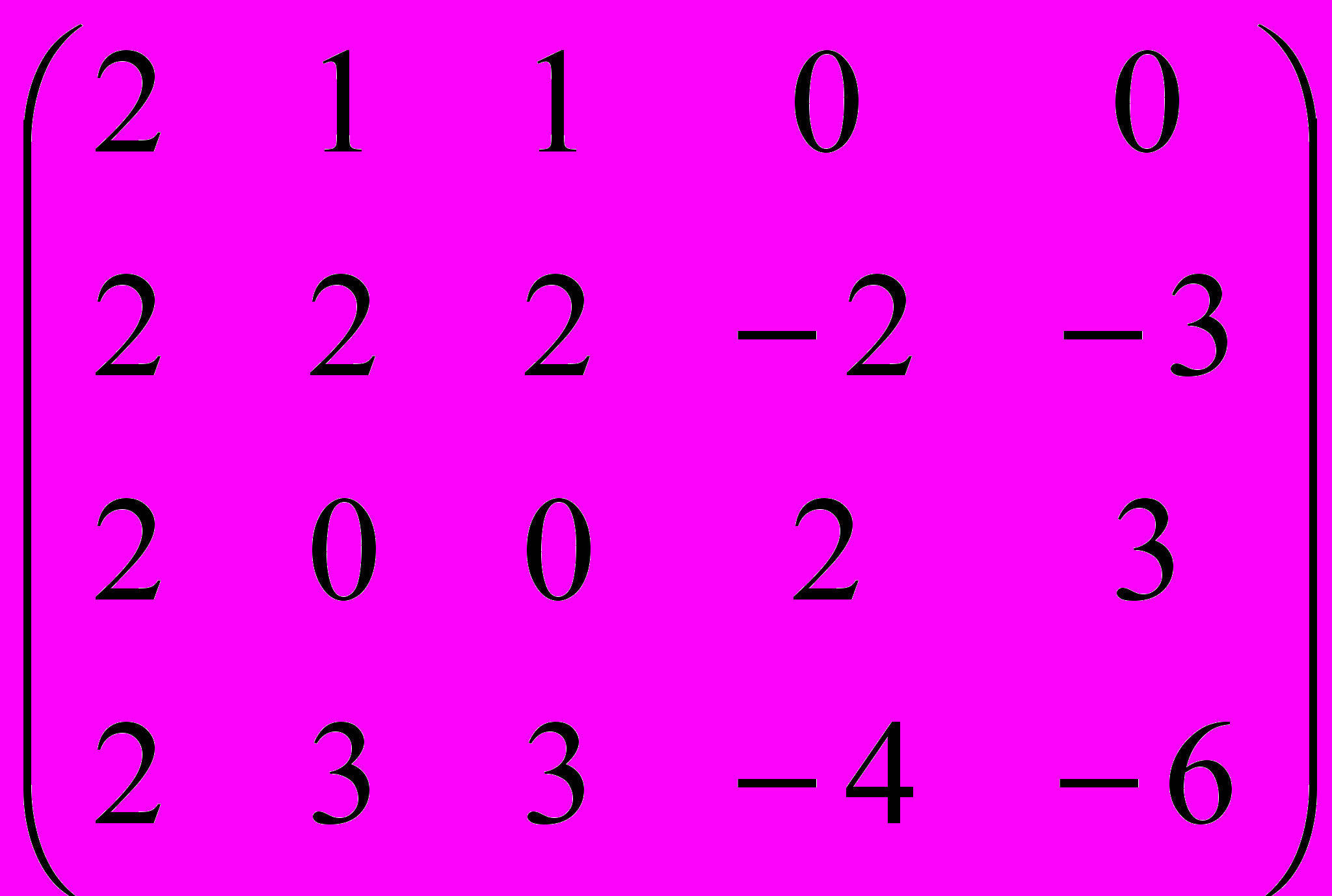 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 11
Паничев
Дана матрица A:
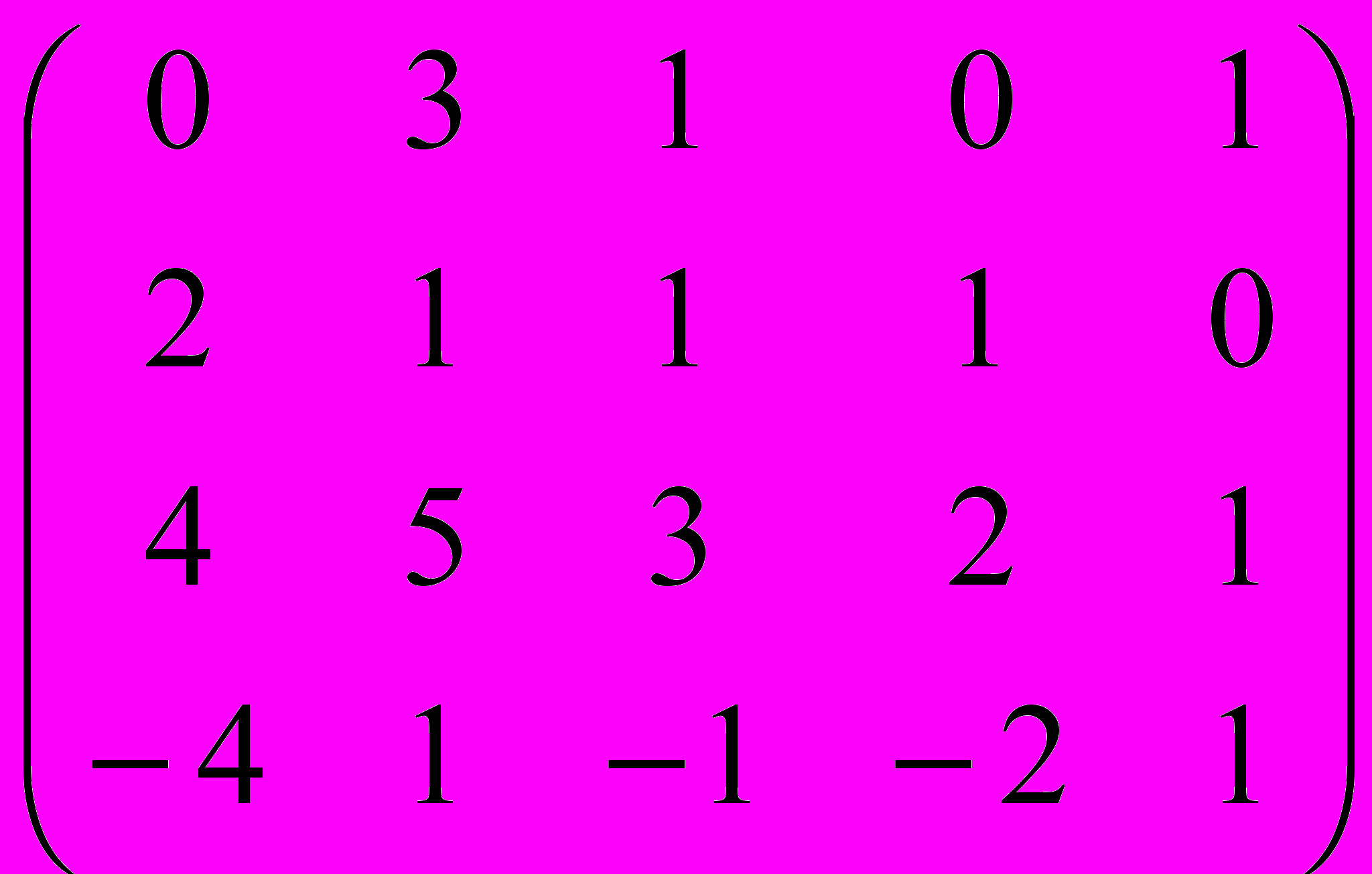 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 12
Пахомов
Дана матрица A:
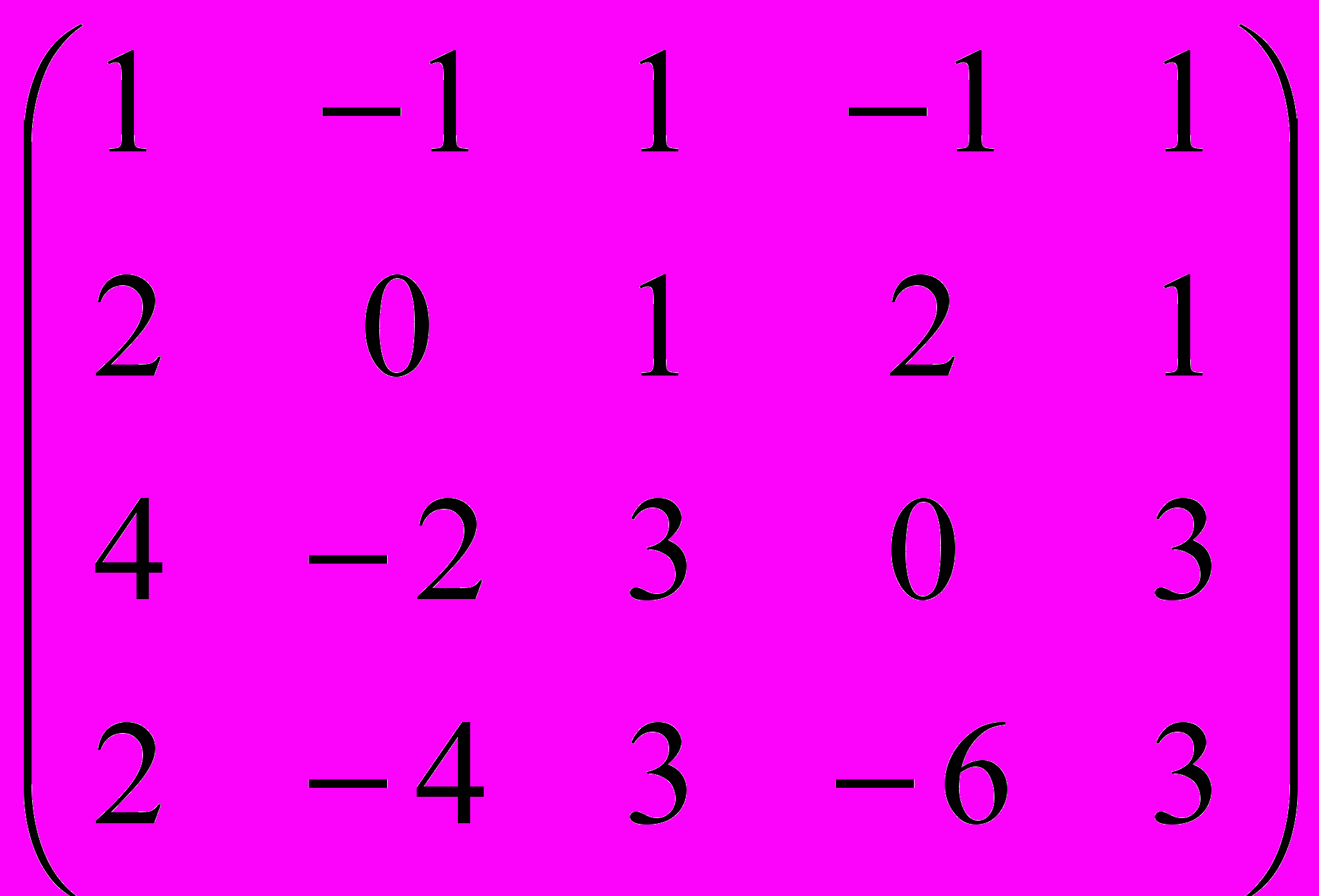 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 13
Ражева
Дана матрица A:
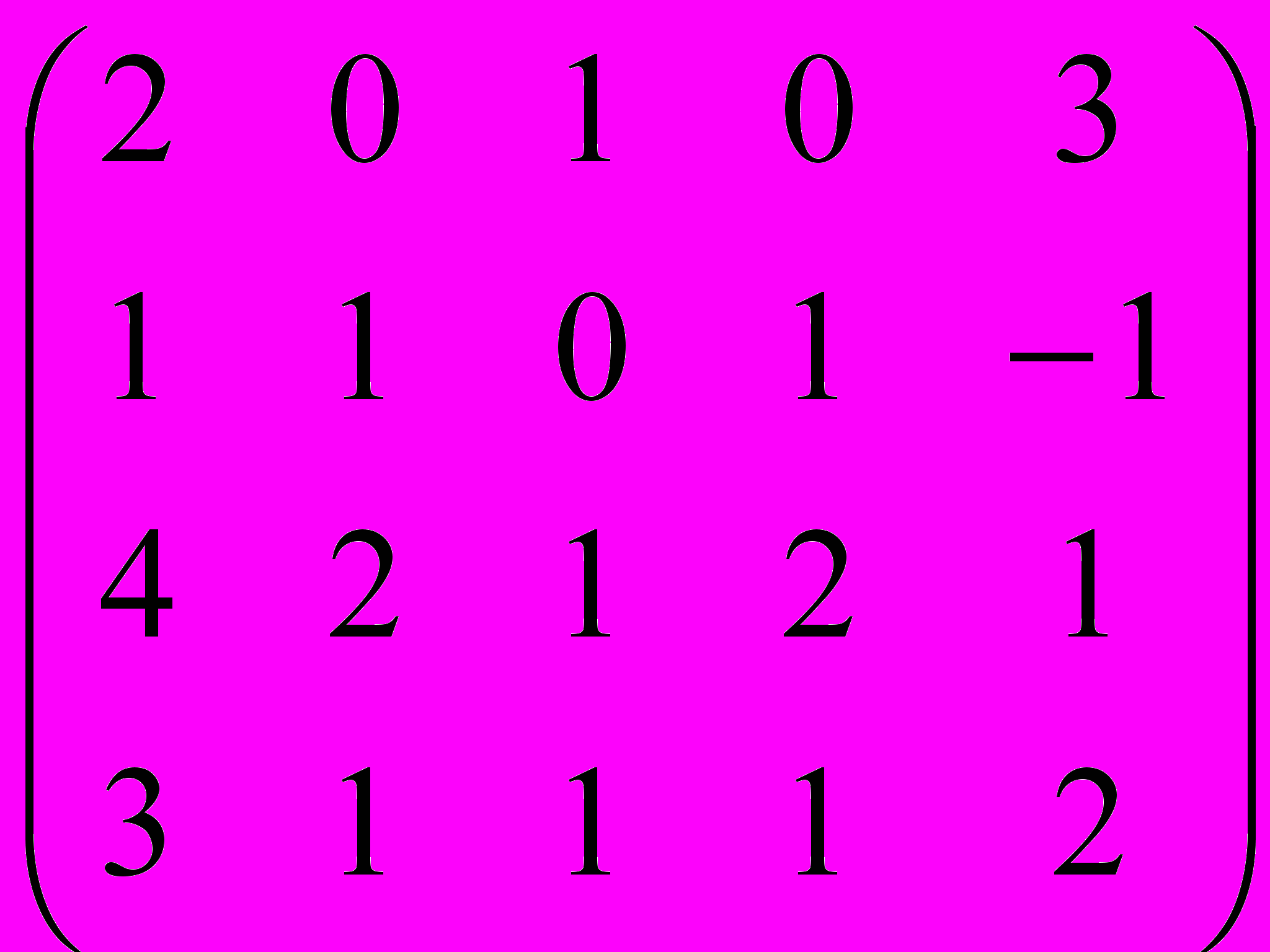 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 14
Сикорская
Дана матрица A:
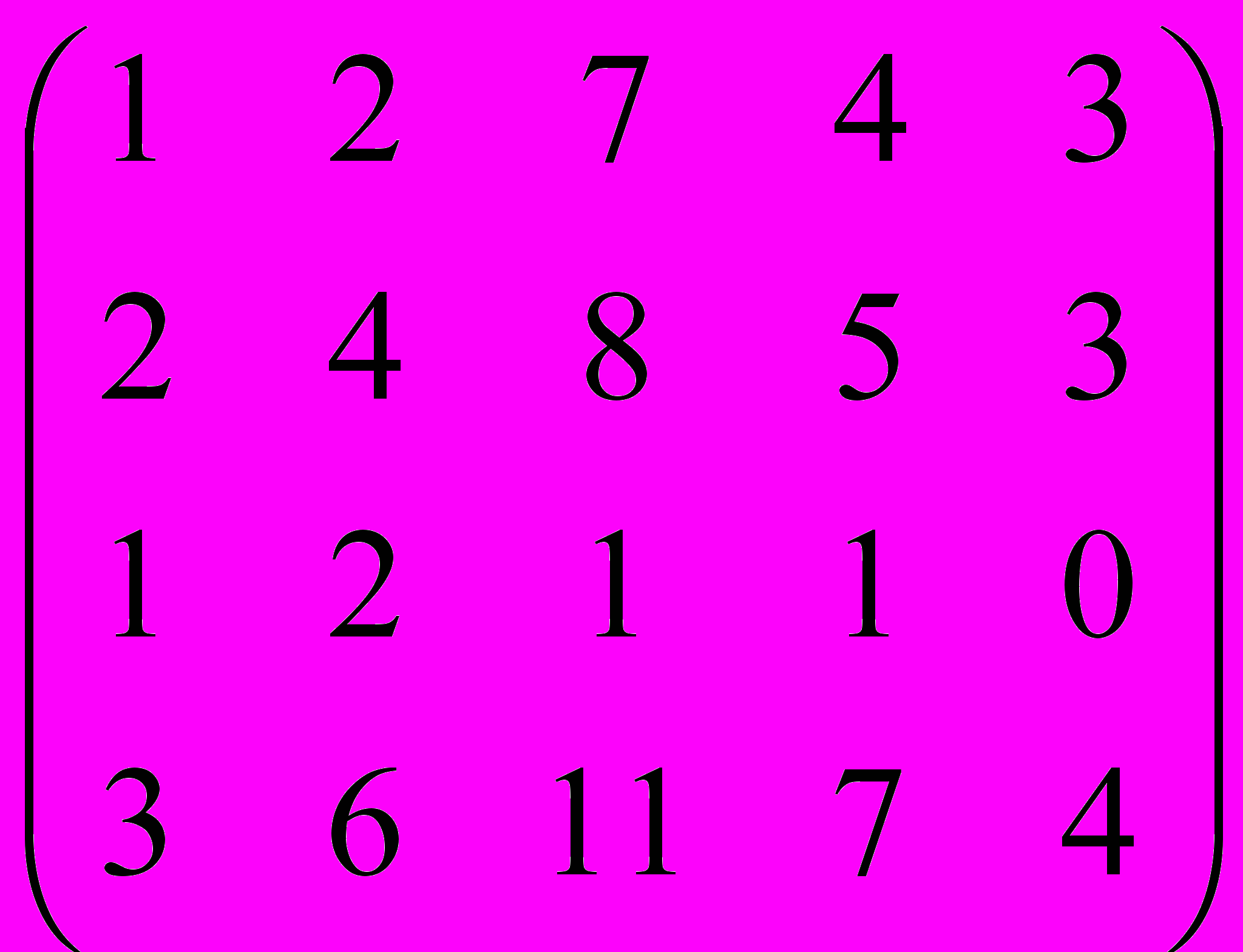 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 15
Сурков
Дана матрица A:
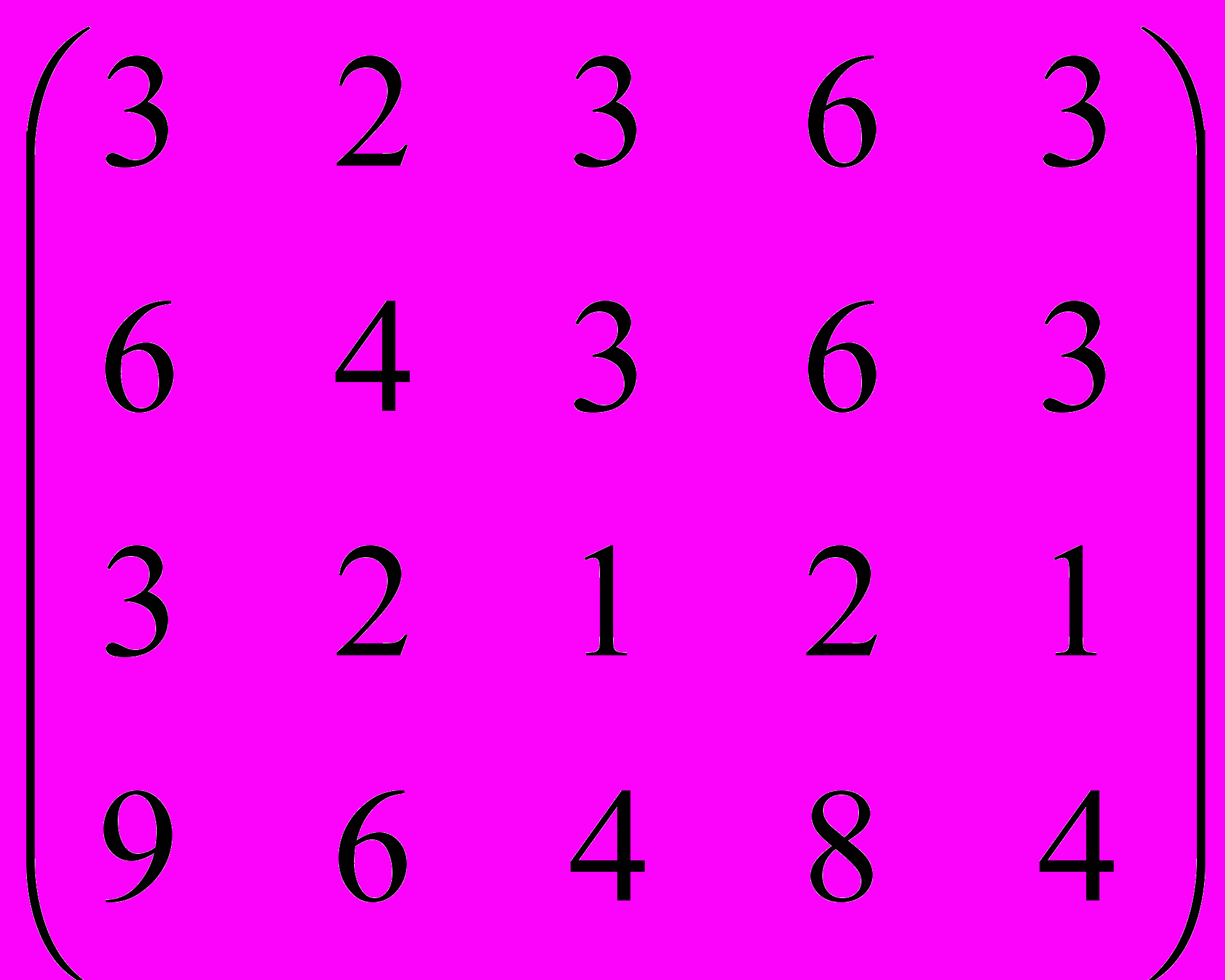 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 16
Горбатов
Дана матрица A:
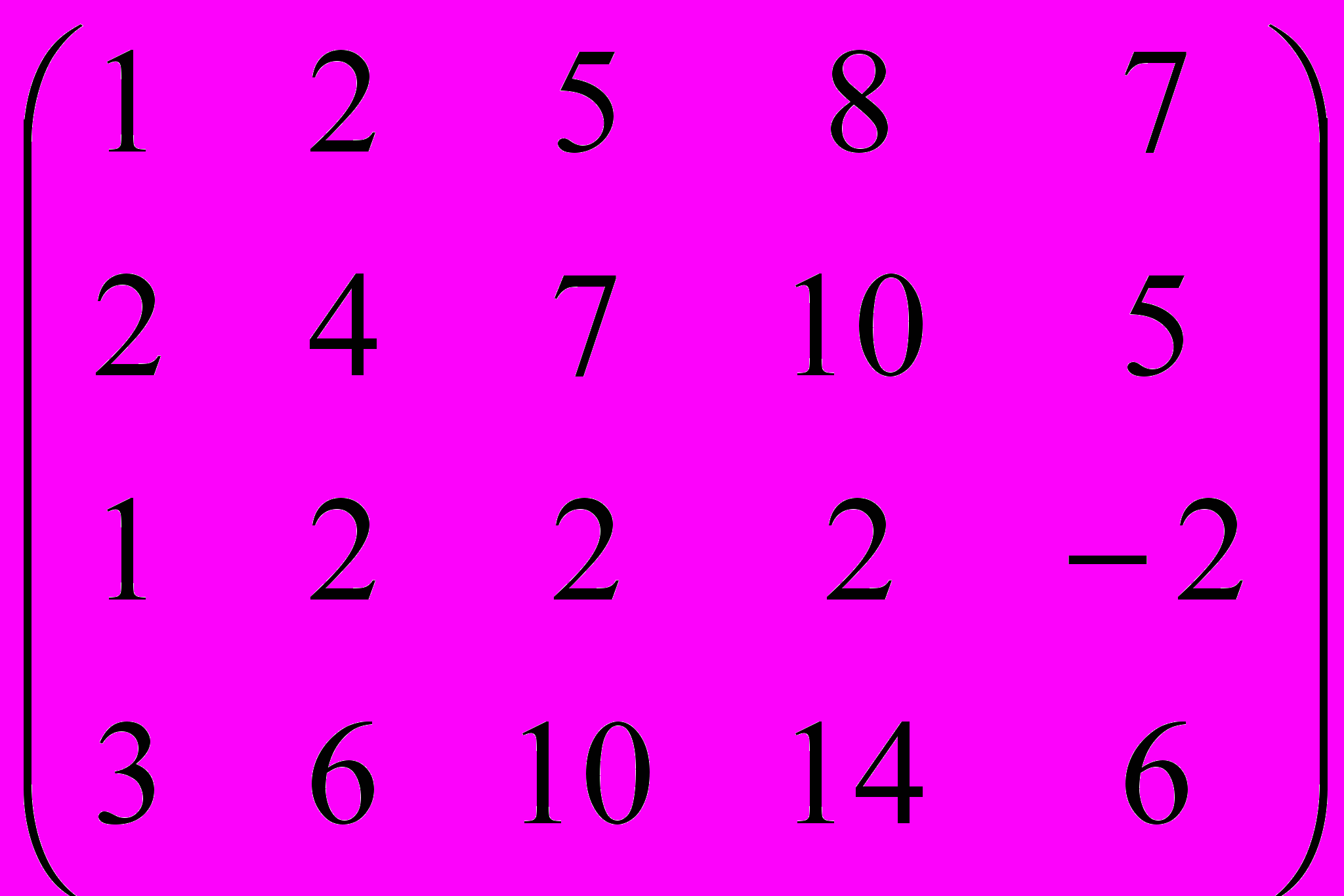 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 17
Зотов
Дана матрица A:
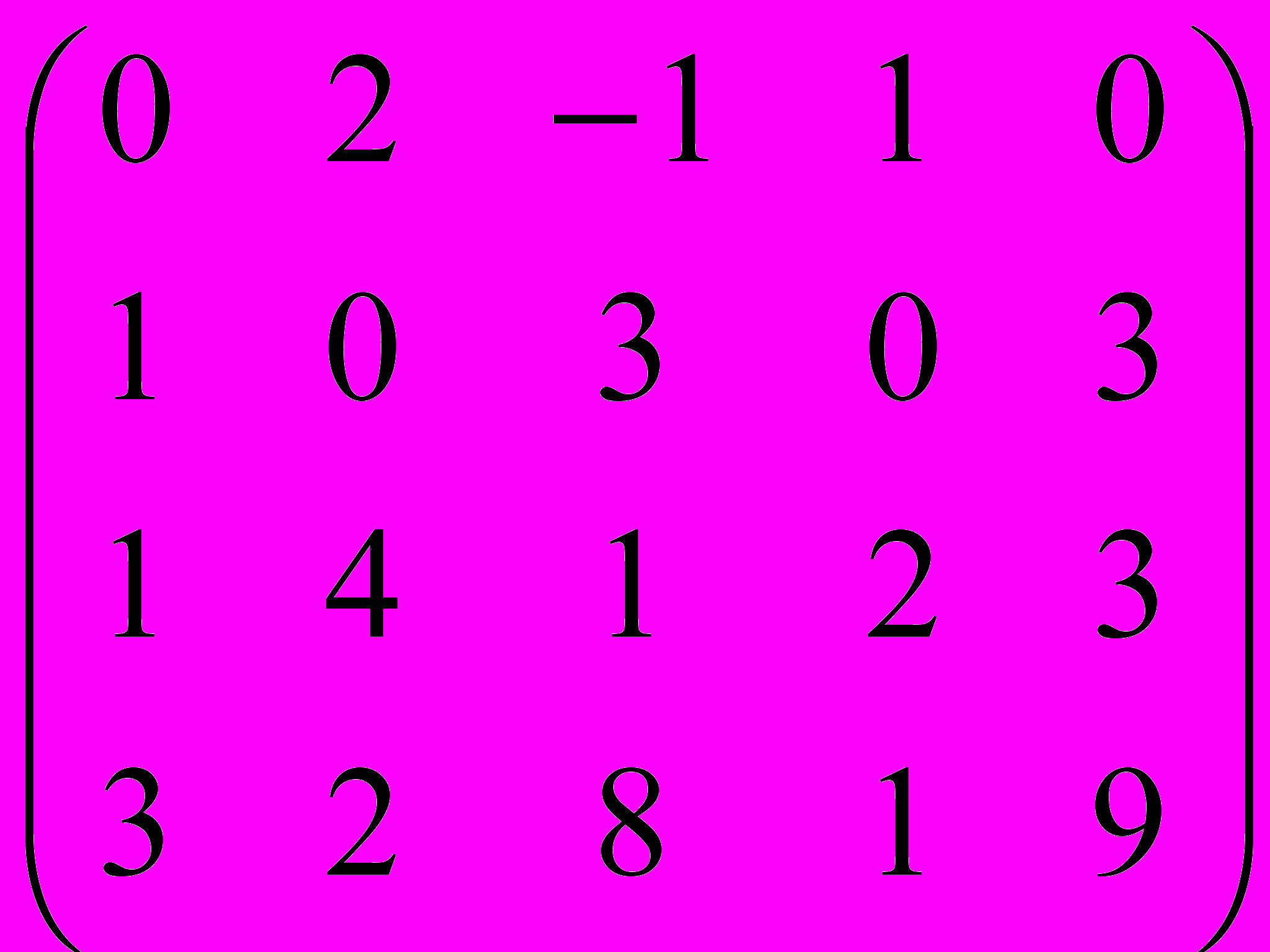 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 18
Иванченко
Дана матрица A:
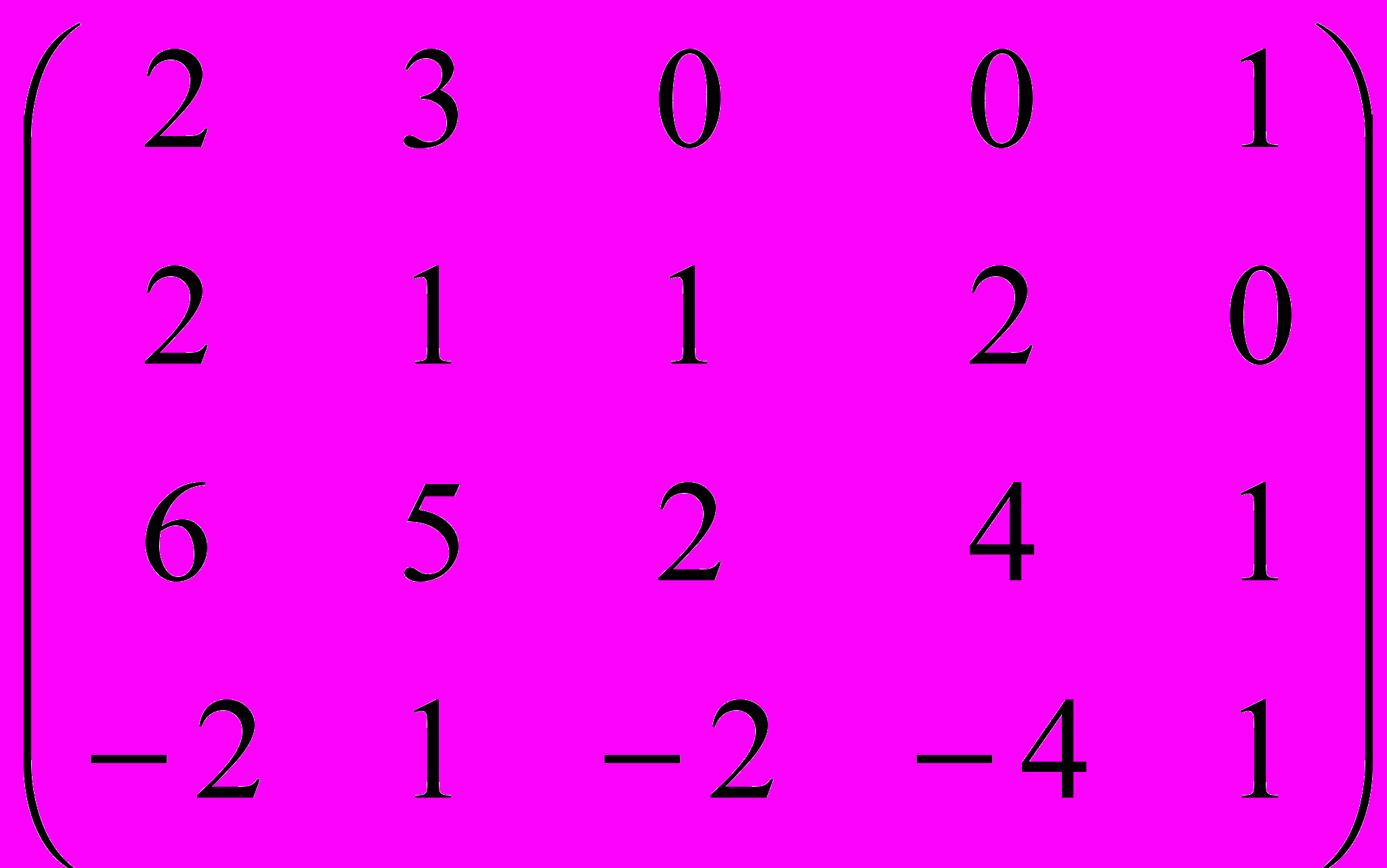 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 19
Исаев
Дана матрица A:
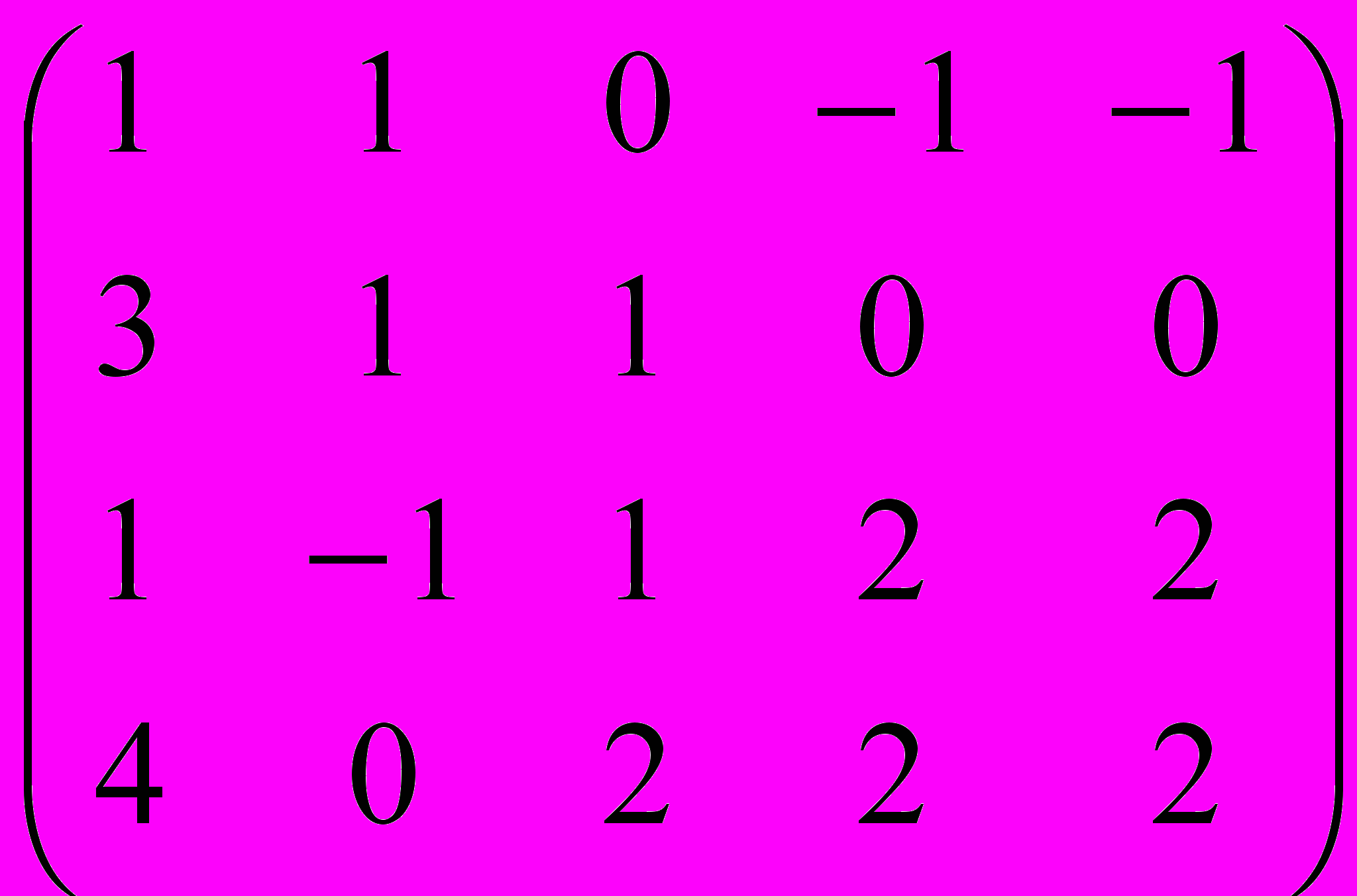 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 20
Камаев
Дана матрица A:
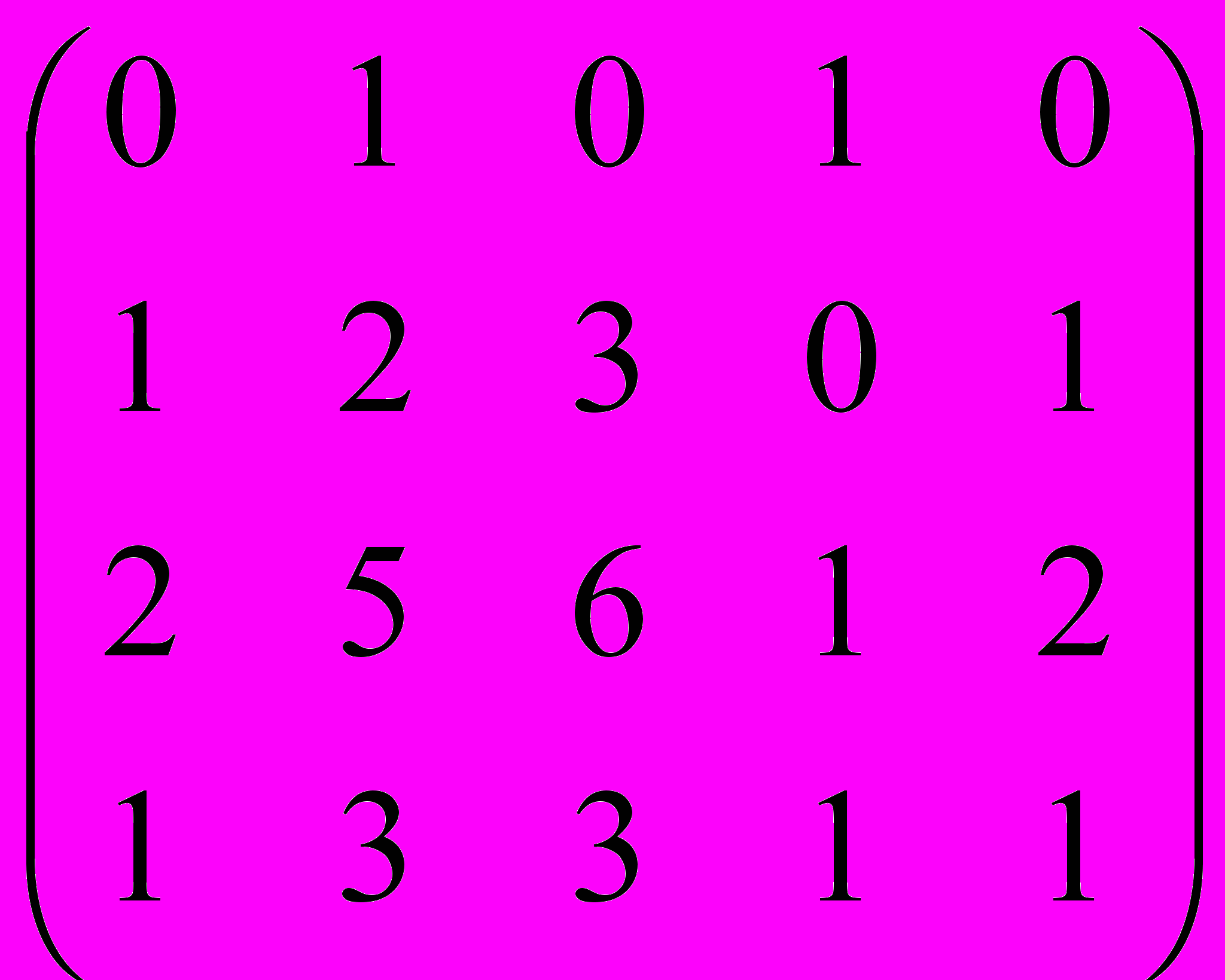 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 21
Капралов
Дана матрица A:
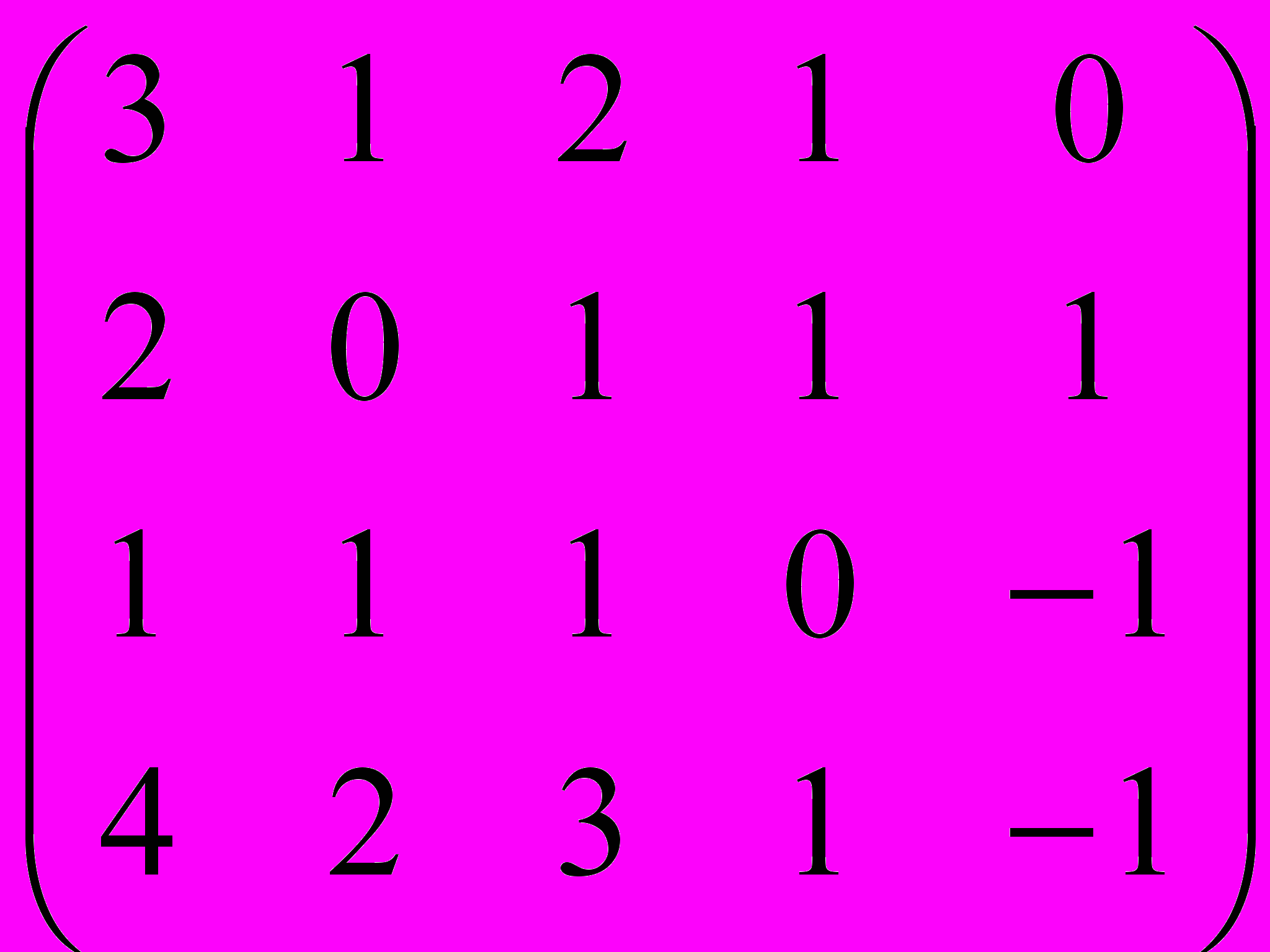 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 22
Маркин
Дана матрица A:
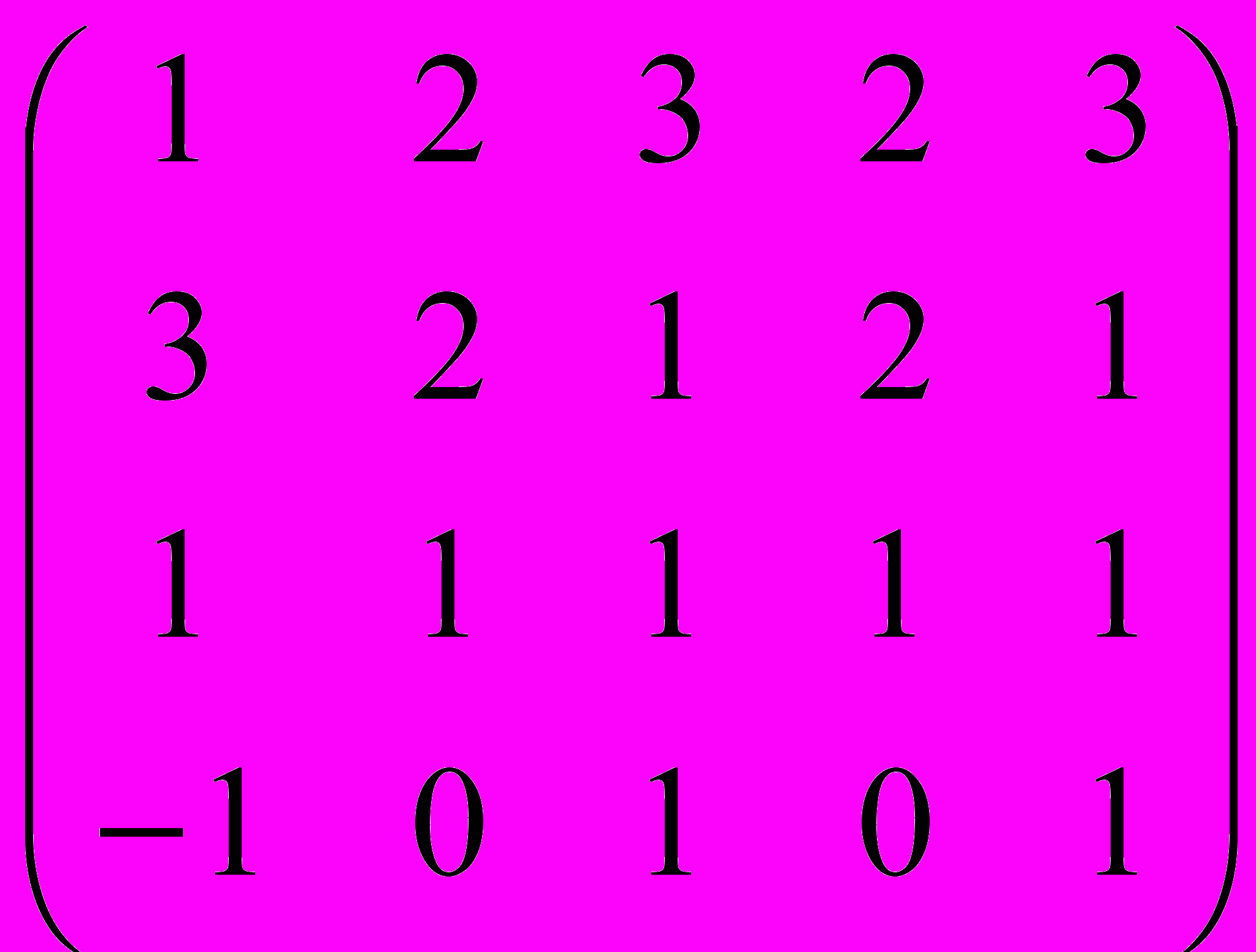 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 23
Мартишин
Дана матрица A:
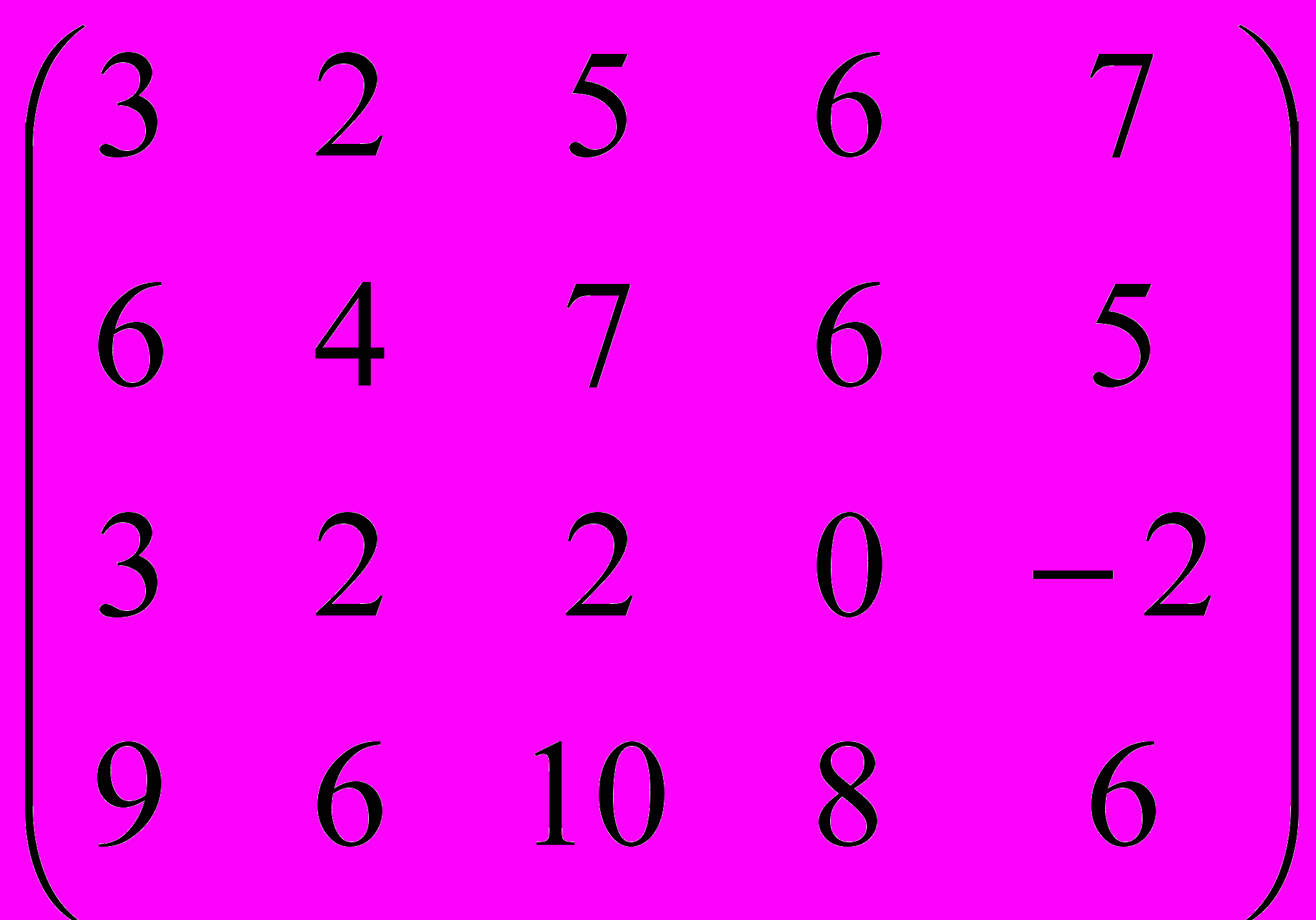 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 24
Пересветова
Дана матрица A:
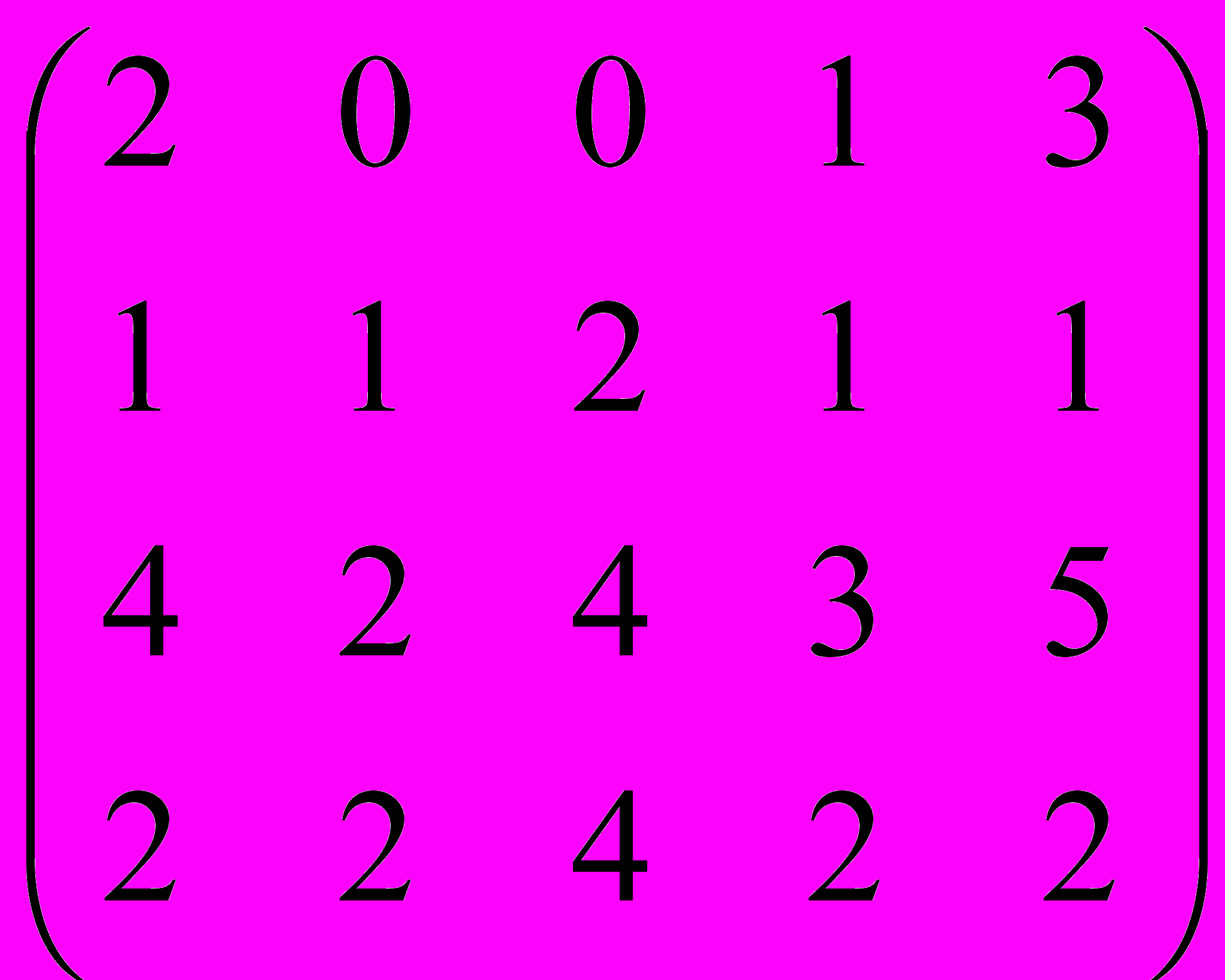 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 25
Скобелева
Дана матрица A:
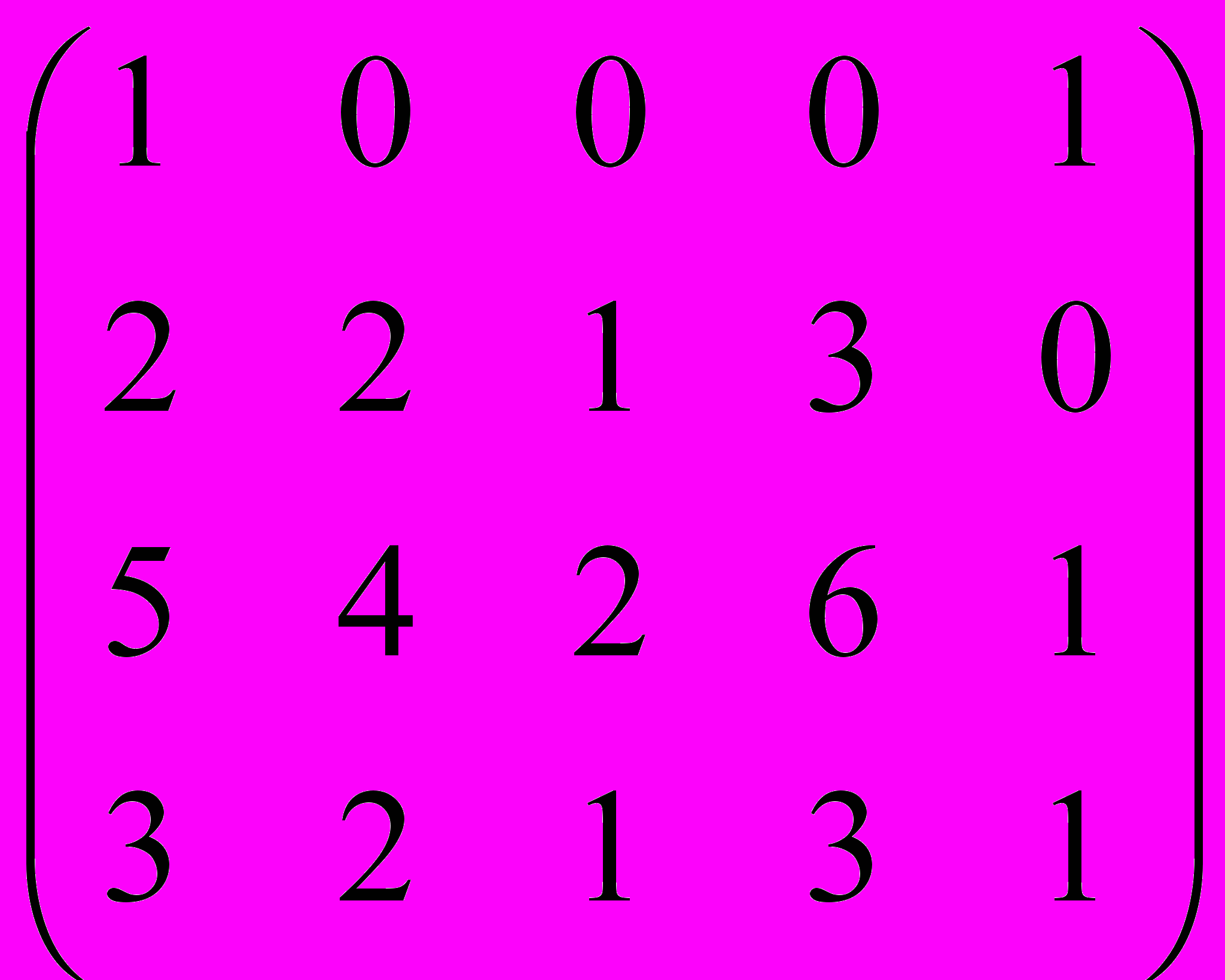 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 26
Ткаченко
Дана матрица A:
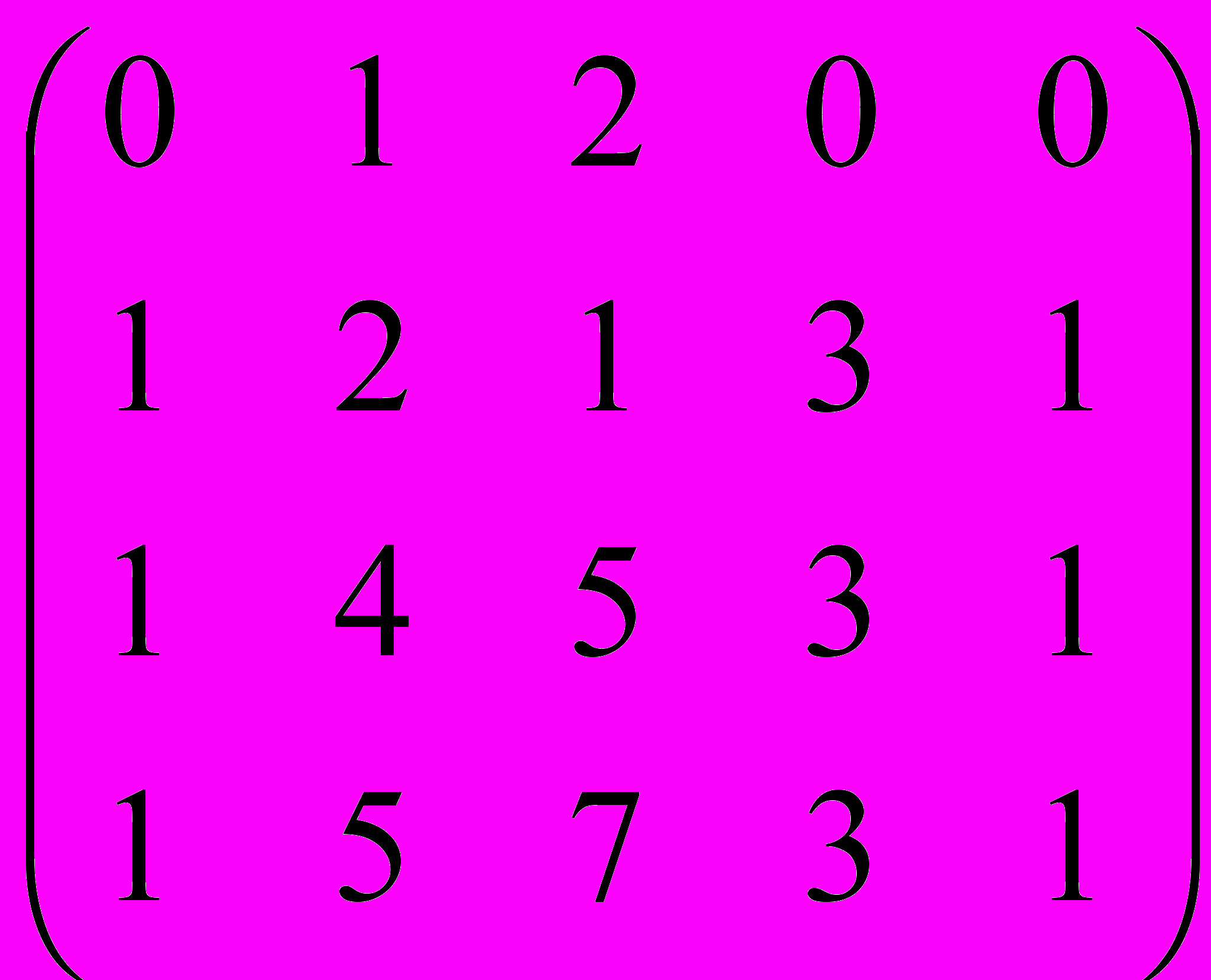 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 27
Трошин
Дана матрица A:
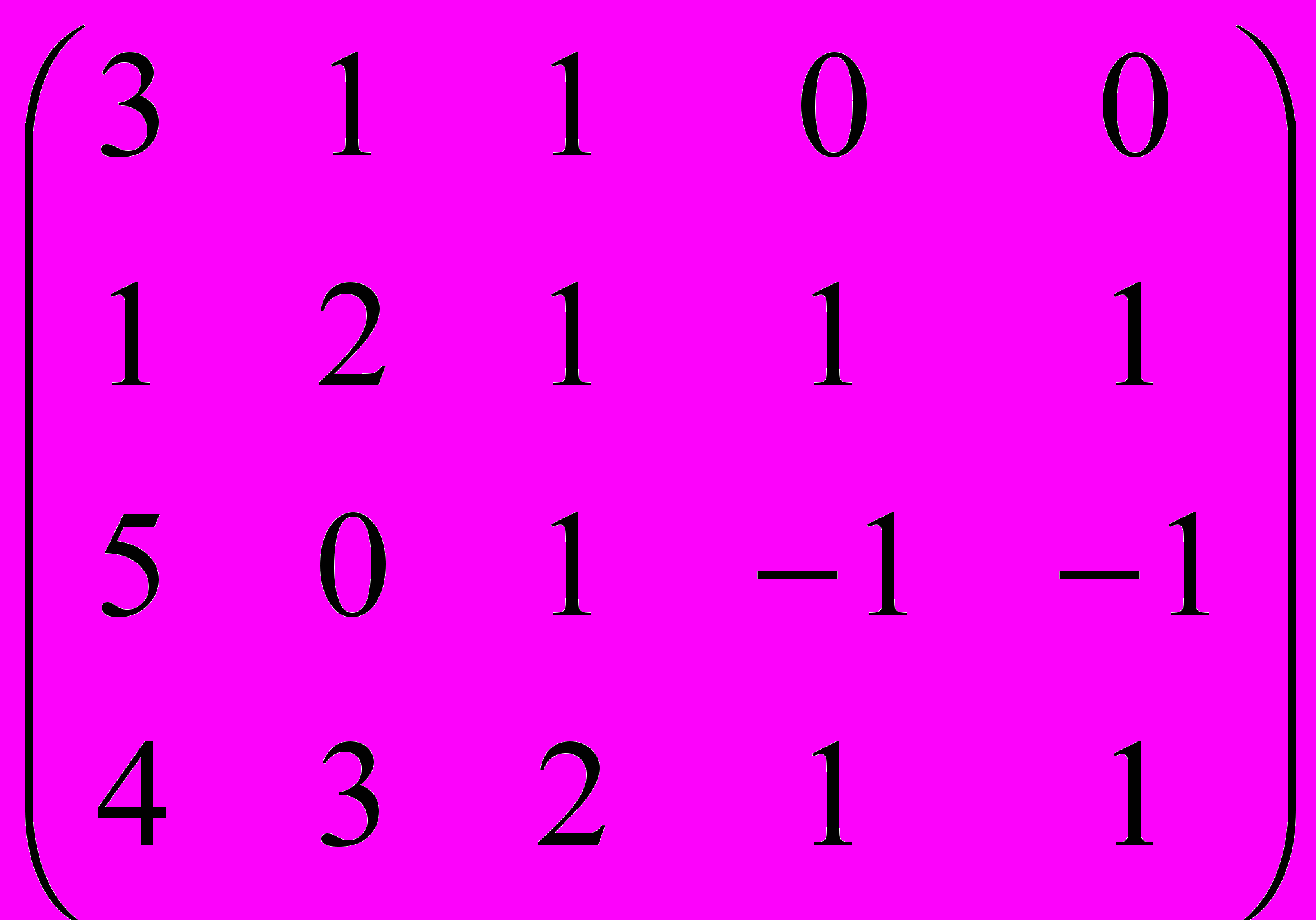 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 28
Фарбовский
Дана матрица A:
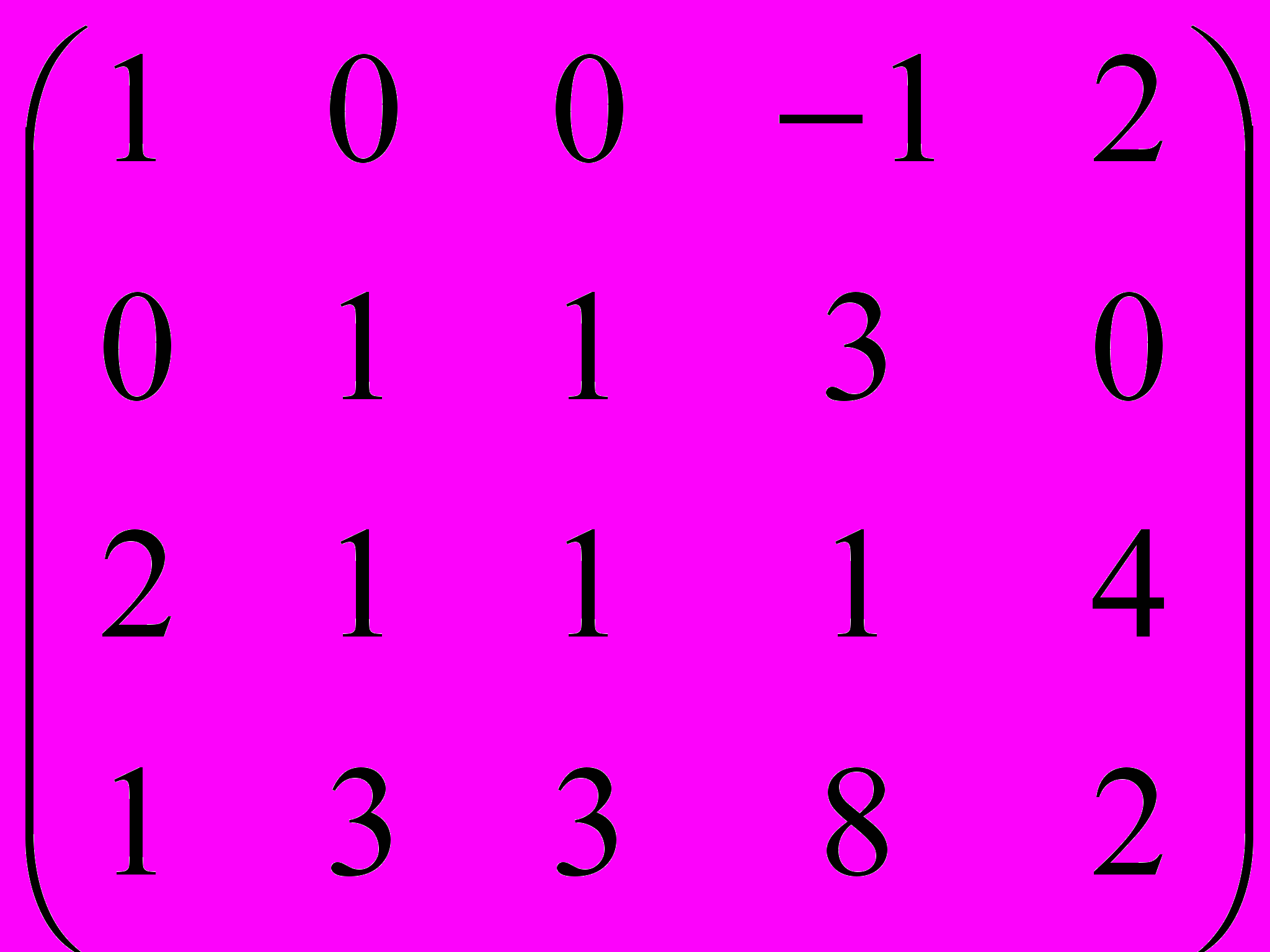 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 29
Дана матрица A:
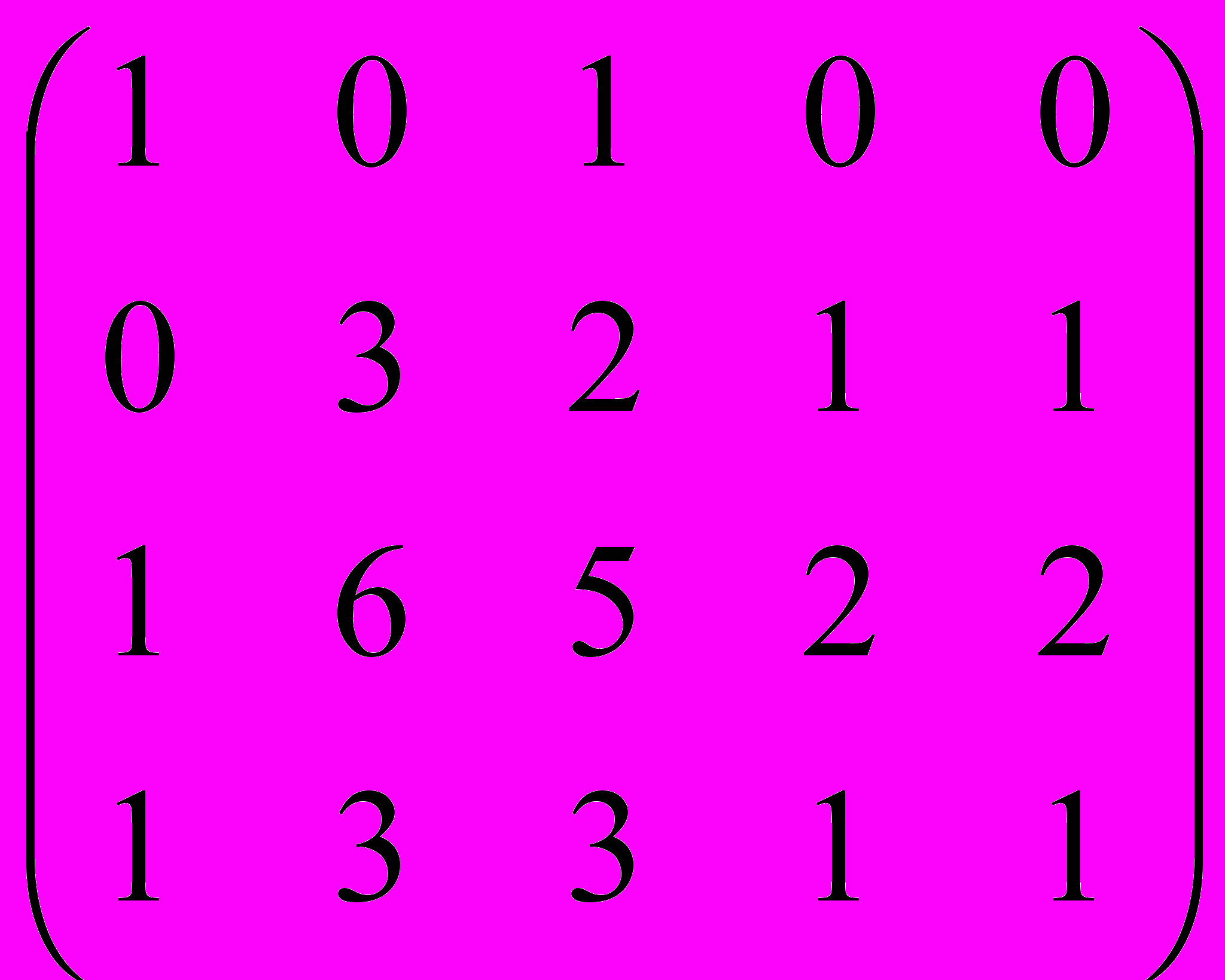 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 30
Дана матрица A:
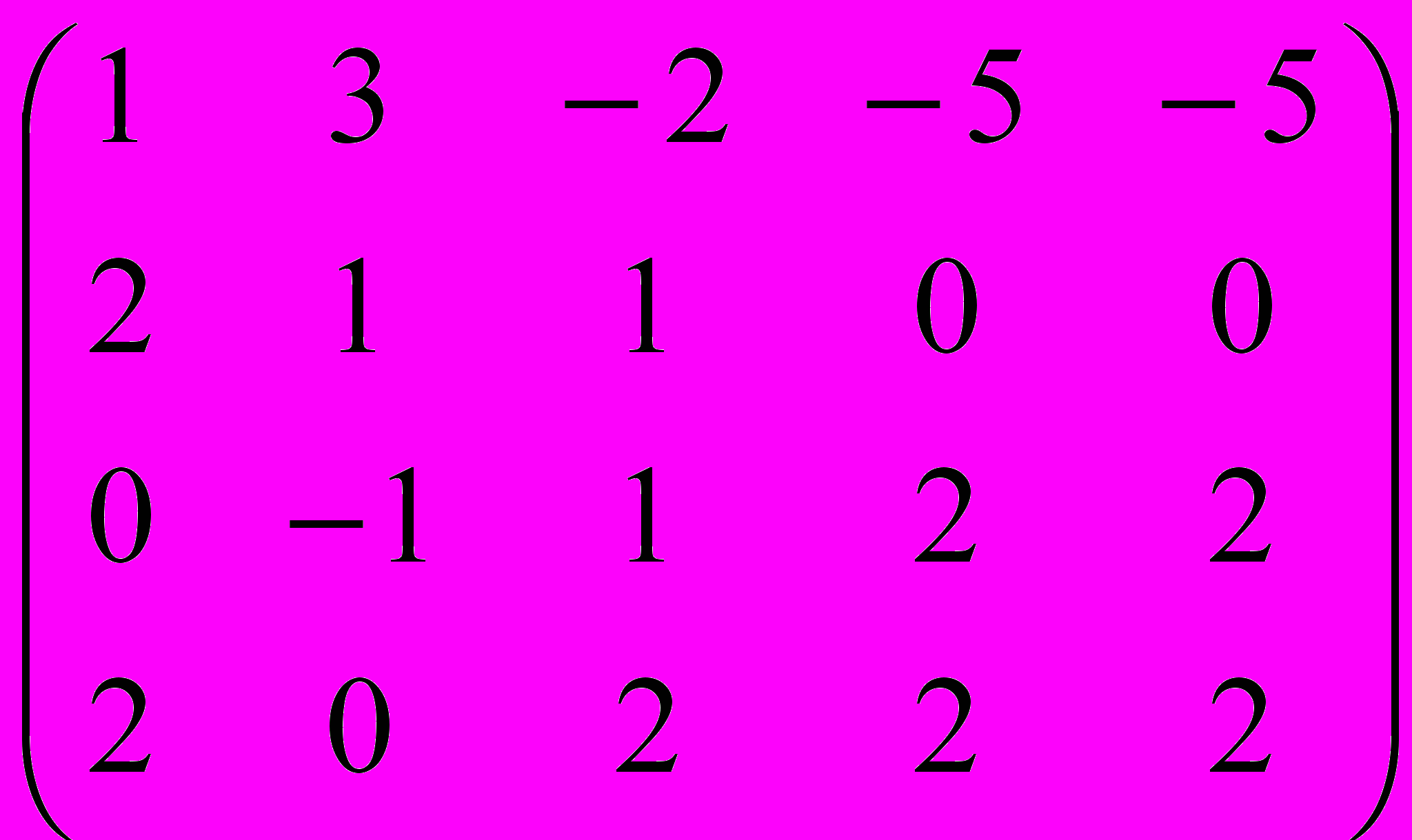 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 31
Дана матрица A:
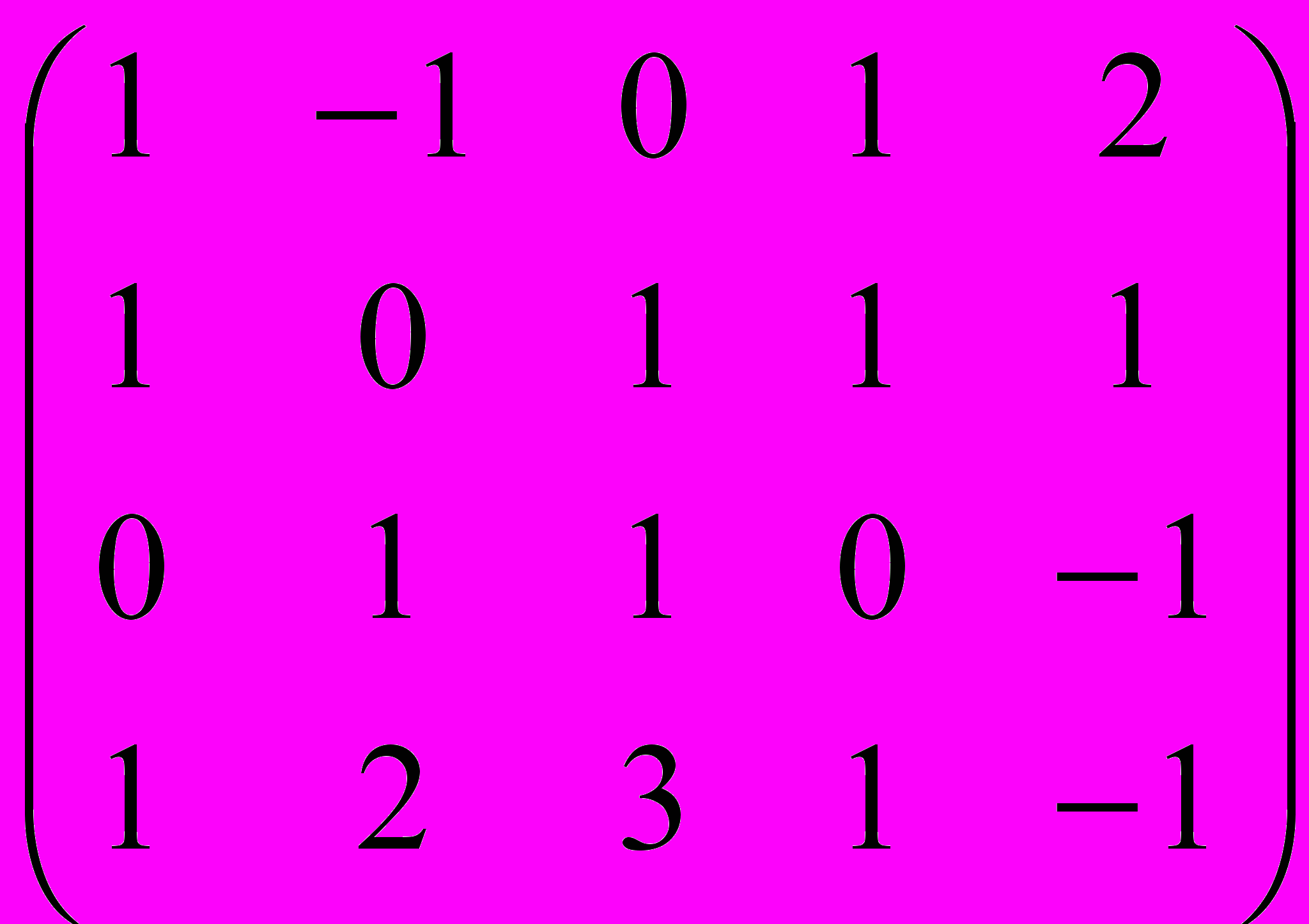 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 32
Дана матрица A:
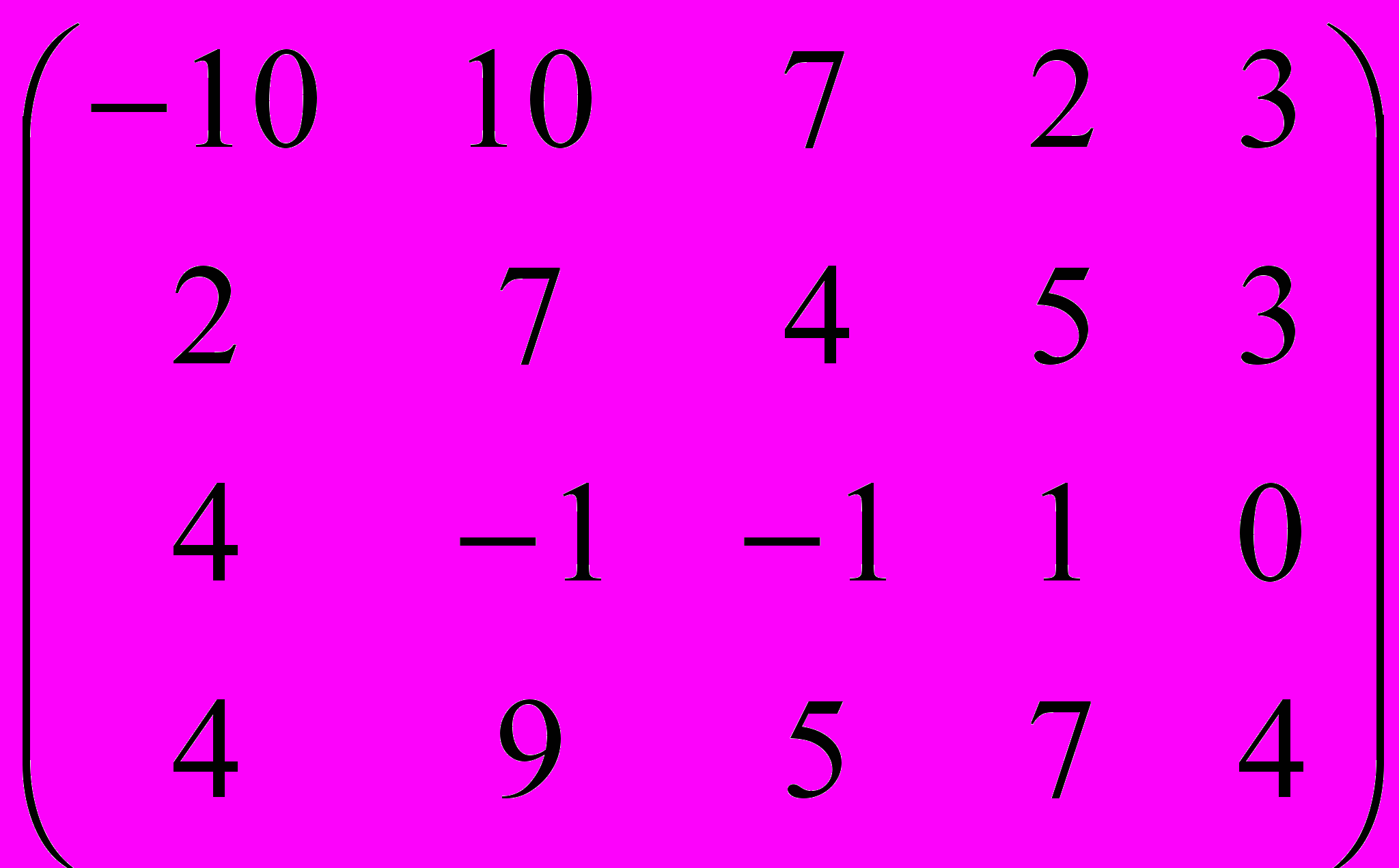 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
Московский институт электроники и математики
Контрольная работа по линейной алгебре и аналитической геометрии
«Системы линейных уравнений»
Осенний семестр 2009 года. К. К. Андреев. Комплект № 1
Билет № 33
Дана матрица A:
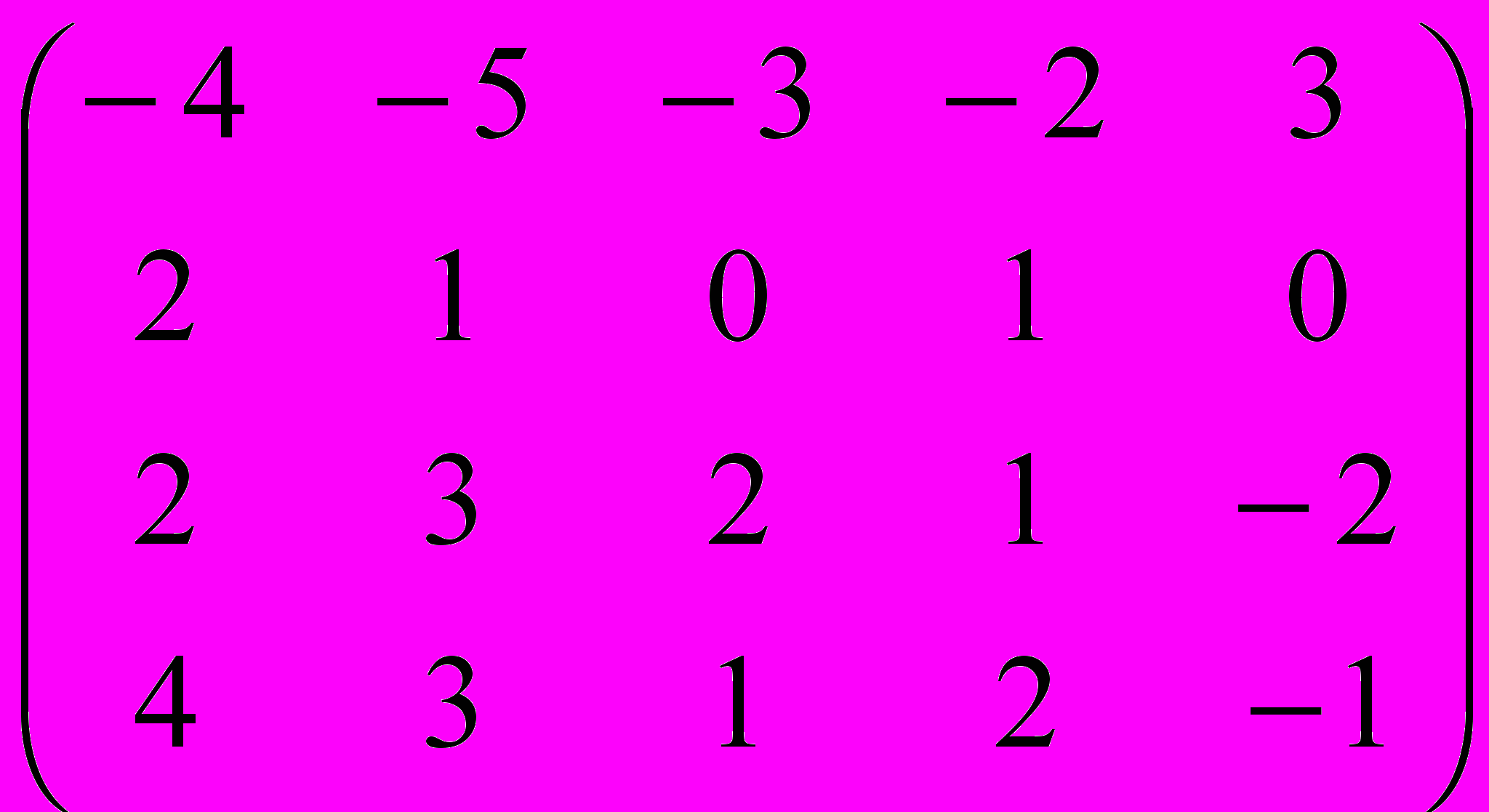 .
.1. а) Записать систему линейных алгебраических уравнений, расширенною матрицею которой служит матрица A.
б) Привести матрицу A с помощью элементарных преобразований над строками и отбрасывания нулевых строк к главной ступенчатой матрице B.
в) Указать, какие неизвестные в системе уравнений, построенной в пункте а), являются главными, а какие − свободными. Найти общее решение этой системы уравнений. Решение выразить в четырёх видах: в виде явных формул, выражающих главные неизвестные через свободные; в векторной форме; в параметрической форме; в векторно-параметрической форме. Найти какое-либо частное решение системы.
г) Записать однородную систему линейных уравнений, соответствующую системе, построенной в пункте а). Найти её общее решение в четырёх видах (см. пункт в)). Найти базис подпространства её решений.
д) Записать общее решение неоднородной системы уравнений как сумму общего решения однородной системы и частного решения неоднородной системы (в векторном виде).
2. а) Найти базис набора столбцов матрицы A.
б) Выразить каждый столбец в виде линейной комбинации базисных столбцов.
в) Найти ранг матрицы A.
