Алгоритм решения системы n линейных уравнений методом Гаусса- зейделя представлен в книге Турчак, Плотников на стр

Вид материала

Содержание

Нелинейные уравнения
Алгоритм итерац. процесса нахождения корня уравнения методом деления отрезка пополам.

Подобный материал:

Алгоритм решения системы n линейных уравнений методом Гаусса- Зейделя представлен в книге Турчак, Плотников на стр. 130

Оценка погрешности приближений процесса итерации:

Пусть x⁽^k^-1) и x⁽^k⁾ (k≥1) – два последовательных приближения решения линейной системы x=αx+β

При р≥1 имеем:

||x⁽^k⁺^p⁾– x⁽^k⁾|| ≤ || x⁽^k⁺^p⁾– x⁽^k⁾|| + ||x⁽^k⁺²⁾– x⁽^k⁺¹⁾||+…+ |x⁽^k⁺^p⁾– x⁽^k⁺^p^-1)|| (5.18)

т.к. x⁽^m⁺¹⁾= αx⁽^m⁾+β и x⁽^m⁾= αx⁽^m^-1)+β,

то x⁽^m⁺¹⁾- x⁽^m⁾=α( x⁽^m⁾ - x⁽^m^-1)) и =>

|| x⁽^m⁺¹⁾- x⁽^m⁾|| ≤ ||α||∙|| x⁽^m⁾ - x⁽^m^-1)|| ≤ ||α||⁽^m^-^k⁾|| x⁽^k⁺¹⁾– x⁽^k⁾|| при m>k≥1

Поэтому из формулы (5.18) получаем

|| x⁽^k⁺^p⁾– x⁽^k⁾|| ≤ ||x⁽^k⁺¹⁾– x⁽^k⁾|| + ||α||∙|| x⁽^k⁺¹⁾ - x⁽^k⁾|| +…

…+||α||⁽^p^-1)|| x⁽^k⁺¹⁾– x⁽^k⁾|| ≤ 1/(1-||α||) ∙ || x⁽^k⁺¹⁾– x⁽^k⁾||

Переходя в последнем неравенстве к пределу при р→∞, получим окончательно:

|| x– x⁽^k⁾|| ≤ || x⁽^k⁺¹⁾– x⁽^k⁾||/(1-||α||) при k≥1 (5.19)

или || x– x⁽^k⁾|| ≤ ||α||/(1-||α||)∙|| x⁽^k⁾– x⁽^k^-1)||

Используя полученные выше оценки для нормы разности двух последовательных приближений, будем иметь:

|| x– x⁽^k⁾|| ≤ ||α||⁽^k⁺¹⁾/( 1-||α||)∙||x⁽¹⁾- x⁽⁰⁾||

В частности, если выбрать x⁽⁰⁾=β, то

x⁽¹⁾=αβ+β, тогда || x⁽¹⁾- x⁽⁰⁾ || = ||αβ||≤||α||∙||β|| =>

|| x- x⁽^k⁾ || ≤ ||α||⁽^k⁺¹⁾/(1-||α||)∙||β|| (5.20)

Пример: Показать, что для данной системы процесс итерации сходится. Сколько итераций следует выполнить, чтобы найти корни системы с точностью до 10:-4

Решение:

И

сходная система

10x₁ – x₂ + 2x₃ – 3x₄ = 0

x₁ + 10x₂ - x₃ – 2x₄ = 5

2x₁ + 3x₂ + 20x₃ – x₄ = -10

3x₁ –2x₂ + x₃ – 20x₄ = 15 (5.21)

П

риведем систему к специальному виду:

x₁= 0.1x₂ – 0.2x₃ + 0.3x₄

x₂ = -0.1x₁ + 0,1x₃ – 0.2x₄ + 0.5

x₃ = -0.1x₁ – 0.15x₂ + 0.05x₄ – 0.5

x₄ = -0.15x₁ – 0.1x₂ – 0.005x₃ – 0.75 (5.22)

Отсюда матрица системы:

0 0,1 -0,2 0,3

α= -0,1 0 0,1 -0,2

-0,1 -0,15 0 0,05

-0,15 -0,1 -0,05 0

Используя, например, L_норму, получим:

||α||_L=max(0.35; 0.35; 0.35; 0.55)=0.55 < 1

Следовательно, процесс итерации для системы (5.22) сходится.

За начальное приближение корня примем:

0

x⁽⁰⁾=β= 0.5

-0.5

0.75

Отсюда

||β||_L= 0 + 0.5 + 0.5 + 0.75 = 1.75

Пусть k – число итераций, необходимое для достижения заданной точности. Применяя формулу (5.20), получим:

||x-x⁽^k⁾|| ≤ (||α||_L⁽^k⁺¹⁾∙||β||_L)/(1-||α||_L) = (0.55^k⁺¹∙1.75)/0.45 < 10^-4

отсюда 0.55^k⁺¹< 45/175∙10^-4и (k+1)∙lg0.55 < lg45 – lg175 – 4

т.е. –(k+1)∙0.25964 < 1.65321 – 2.24304 – 4 = -4.58983 =>

k+1 > 4.58983/0.25964 ≈ 17.7 и k > 16.7 можно принять k=17.

Следует отметить, что теоретически оценка числа итераций, необходимых для обеспечения заданой точности, практически оказывается весьма завышенной.

Большое число научно-технических задач, а также некоторые исследования в области выч. лог-ки требует нахождения собств. значений и собств. векторов матриц. Однако эти вопросы остаются за рамками курса.

Нелинейные уравнения

Уравнения с одним неизвестным:

Задача нахождения корней нелинейного уравнения вида F(x)=0 (6.1)

встречается в различных областях научных исследований (здесь F(x) – некоторая непрерывная функция). Нелинейные уравнения можно разделить на 2 класса – алгебраические и трансцендентные.

Алгебраическими называются уравнения содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, мн-н является целой целой алгебраической функцией. Уравнения содержащие другие функции (тригонометрические, показательные, логарифмические и д.р.) называются трансцендентными.

Методы решения нелинейных уравнений делятся на прямые и итерационные.

Прямые методы позволяют записывать корни в виде некоторого конечного соотношения(формулы). Однако встречающиеся на практике уравнения не удается решить такими простыми методами. Для их решения используют итерационные методы, т.е. методы последовательных приближений. Как и в случаях СЛАУ, алгоритм нахождения корня нелинейного уравнения с помощью итерационного метода состоит из двух этапов:

Нахождение приближенного значения корня(начального приближения)
Уточнение приближенного значения до некоторой заданной степени точности. В некоторых методах отыскивается не начальное приближение, а некоторый отрезок, содержащий корень.

Начальное приближение может быть найдено различными способами: из физических соображений, из решения аналитической задачи при других исходных данных, с помощью графических методов.

Е

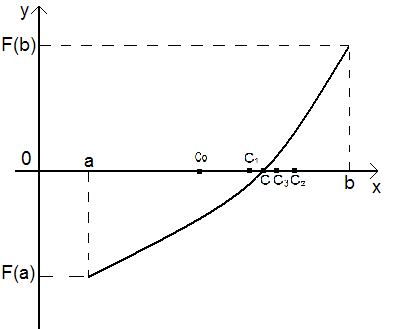
сли такие алгоритмы оценки исходного приближения провести не удается, то находят две близко расположенные очки a и b, в которых непрерывная функция F(x) принимает значения разных знаков, т.е. F(a)∙ F(b)<0. В этом случае между точками a и b по крайней мере одна точка, в которой F(x)=0.

В качестве начального приближения x⁽⁰⁾можно принять середину отрезка

[a, b], т.е. x⁽⁰⁾=(a+b)/2. Общую схему итерац. методов мы уже рассмотрели. Итерац. процесс состоит в последовательном уточнении начального приближения.

Каждый шаг называется итерацией. В результате итераций находится последовательность приближенных значений корня x₁, x₂,…, x_k, …

и если эти значения с ростом k стремятся к истинному значению корня

lim_k_→∞x⁽^k⁾=x

то говорят, что итерац. процесс сходится. В отличие от случая СЛАУ x⁽^k⁾скаляр, а не вектор, поэтому пока номер итераций будем обозначать нижний индексом x_k.

Рассмотрим некоторые итерационные методы решения трансцендентных уравнений.

Один из простейших методов нахождения корней уравнения нелинейных

уравнений - метод деления отрезка пополам (метод бисекции)

(У Парумова метод дихотомии)

Д

опустим, нам удалось найти [a, b], на котором расположено искомое значение корня x=c, c [a, b]

Мы будем предполагать, что x=c – единственный корень на [a, b]. В противном случае можно выбрать меньший [ ].

В качестве начального приближения корня принимаем середину этого отрезка c₀=a+b / 2. Далее исследуем значения ф-ии F(x) на концах отрезков [a, c₀] и [c₀, b], т.е. F(a), F(c₀), F(b). Тот из отрезков, на конце которого F(x) принимает значения разных знаков, содержит искомый корень. Этот отрезок принимает в качестве нового [a₁, b₁]. Вторую половину [a, b], на которой знак F(x) не меняется, отбрасываем. В качестве первого приближения корня принимаем середину нового отрезка c₁=a₁+b₁ / 2 и т.д.

Т.о к-е приближение вычисляется так c_k=a_k+b_k / 2(6.2)

После каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а после «К» итерации он сокращается в 2^к раз:

b_k-a_k=b-a / 2^k (6.3)

Пусть приближенное решение x_* требуется найти с точностью до некоторого значения числа ε>0:

|х-х_k|< ε (6.4)

Взяв в качестве приближения решения к-е приближение корня x_*=c_k, с учетом обозначения x=c (6.4) запишем в виде:

|c-c_k|< ε (6.5)

Из (6.2) следует, что (6.5) выполнено, если b_k-a_k<2ε (6.6)

Т.о. мы получим условие, до выполнения которого необходимо продолжать итерационный процесс.

Метод деления отрезка пополам всегда сходится(в отличие от большинства других методов), причем можно гарантировать, что полученное решение будет иметь наперед заданную точность (в рамках разрядности компьютера).

однако метод бисекции довольно медленный. Вычислим число итераций требуемое для достижения точности ε.

Пользуясь (6.3), выясним, для каких k выполнимо условие (6.6), и возьмем наименьшее из таких k. Окончательно получим:

k>log₂(b-a/2ε)

N=E(log₂(b-a/2ε))+1 (6.7)

Где Е(х) – целая часть числа х. обычно для метода деления отрезка пополам N большее, чем для некоторых других методов, что не является препятствием к применению этого метода, если вычисление значений функции F(x) несложно.

Итерационный процесс можно завершать и тогда, когда значение функции F(x) после k^ой итерации станет по модулю меньше ε

|F(x)| < ε (6.8)

Алгоритм итерац. процесса нахождения корня уравнения методом деления отрезка пополам.

ввод a, b, ε

вычисление F(а)

п

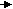ока b-a ≥ 2ε

c=(a+b)/2

вычисление F(c)

да нет

F(a)· F(c)>0

a=c

b=c

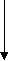
c=(a+b)/2

вывод с

Метод хорд (У Пирумова: метод секущих)

Пусть мы нашли [a, b], на котором функция F(х) меняет знак. Для определения примем

F(а) > 0, F(b) < 0

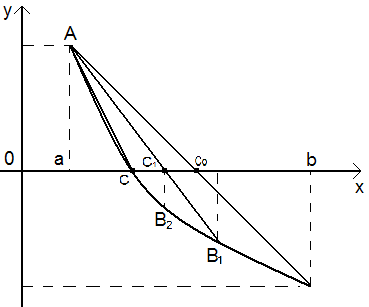
В данном методе процесс итераций состоит в том, что в качестве приближения корню уравнения (6.1) принимаются хорды с осью абсцисс.

Уравнение хорды АВ:

(y-F(а))/(F(b)-F(а)) = (х-а/(b-а)

Для точки её пересечение с осью абсцисс (х=с₀, y=0) получим уравнение:

с₀=а – ((b-а)/(F(b)-F(а))∙F(а) (6.9)

Далее, сравним знаки величин F(а) и F(с₀) для рассматриваемого случая, делаем вывод что корень находится в интервале (а, с₀), т.к. F(b)∙(а)<0.

Отрезок [с₀, b] отбрасываем. Следующая итерация состоит в определении нового приближения с₁ как точки пересечения хорды АВ₁ с осью абсцисс и т.д. Здесь условие окончания итераций типа (6.6) неприменимо.

На рисунке хорошо видно, что длина [а, с_k] никогда не станет меньше длины [а, с].

Здесь нужно использовать условие близости двух последовательных приближений:

|c_k-c_k-1|<ε (6.10)

Или условие малости невязки (6.8). Метод бисекции и метод хорд похожи, в частности процедурной проверки знаков функции на концах [ ]. При этом метод хорд в ряде случаев дает более быструю сходимость итерационного процесса. Оба метода не требуют знания дополнительной информации о функции F(х), достаточно условия непрерывности F(х).

Более сложный метод решения нелинейного уравнения требует дополнительной информации о функции F(х), например диф-ть.

Они обычно обладают более быстрой сходимостью, но применимы для более узкого класса функций, и сходимость их не всегда гарантирована.

Примером такого метода может быть метод Ньютона(метод касательных).

Отличие от метода хорд, на k^ойитерации вместо хорды строится касательная к кривой y=F(х) при х=с_k_-1 и ищется точка пересечения касательной с осью абсцисс. При этом не обязательно задавать [а, b], достаточно лишь найти некоторое начальное приближение корня х=с₀.

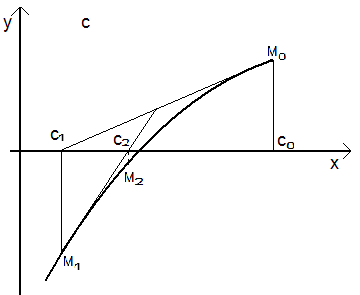
Уравнение касательной, проведенной к кривой y=F(х) в точке М₀ с координатами (с₀, F(с₀)) имеет вид:

y-F(с₀)=F’(с₀)(х-с₀)

отсюда находим следующее приближение корня с₁ как абсциссу точки пересечения касательной с осью х (y=0)

с₁=с₀-F(с₀)/F’(c₀)

Аналогично находят следующее приближения как точки пересечения с осью M₁, M₂… Формула для k^гоприближения

с_k=c_k-1-F(c_k-1)/F’(c_k-1) k=1, 2,… (6.11)

Необходимо, чтобы F’(с_k_-1)≠0.

Для окончания итерационного процесса можно использовать условия (6.10) или (6.8).

Из (6.11) следует, что объем вычислений на каждой итерации метода Ньютона больше, чем в расмотреных ранее методах, т.к. приходится вычислять F(х) и F’(x). Однако скорость сходимости здесь значительно выше.

Имеет место след теорема:

Пусть х=с – корень уравнения (6.1), т.е. F(с)=0, а F’(с)≠0 и F’’(x) непрерывна.

Тогда существует окрестность D корня с (с є D) такая, что если начальное приближение с₀ принадлежит этой окрестности, то для метода Ньютона последовательность приближения {c_k} сходится к с при k→∞

При этом для погрешности корня ε_k=с-с_kимеетместо соотношение

lim_k_→∞|ε_k/ ε²_k_-1| = |F”(c)/2F’(c)|

Трудность применения метода Ньютона состоит в выборе начального приближения, k^ое должно находиться в окрестности D. При неудачном выборе начального приближения итерации могут расходиться.

Пример:

для уравнения arctg(x)=0 (корень х=с=0) при начальном приближении с₀=1.5 первые 6 итераций приводят к погрешностям:

ε₁=1.69; ε₂=-2.32; ε₃=5.11; ε₄=-32,3; ε₅=1.58∙10³; ε₆=-3.89∙10⁶

Очевидно, итерации расходятся.

Для предотвращения расходимости иногда целесообразно использовать смешанный алгоритм:

сначала применяется всегда сходится метод(напр. метод деления отрезка пополам), а после некоторого числа итераций – быстро сх-ся м-д Ньютона.

Blog

Алгоритм решения системы n линейных уравнений методом Гаусса- зейделя представлен в книге Турчак, Плотников на стр

Содержание