Лабораторная работа n 3

Вид материала

Содержание

Алгоритмы методов и примеры их реализации в электронной таблице
Прямой ход
2 шаг: выполняем те же действия с матрицей А, не трогая ее 1 строку и 1 столбец, т.е. работаем с матрицей порядка n-1
Метод прогонки
Прямой ход

Подобный материал:

ЛАБОРАТОРНАЯ РАБОТА N 3

Прямые методы решения систем линейных уравнений

Задание

Решить систему линейных уравнений из работы № 2 методом Гаусса (схема единственного деления)
Решить систему линейных уравнений из работы № 2 методом Гаусса (схема оптимального исключения)
Решить систему методом прогонки

Вариант	Система	Вариант	Система
1 2 3 4 5		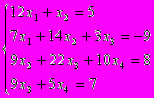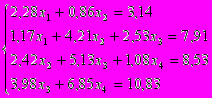6 7 8 9 10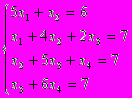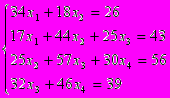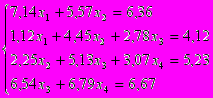

Примечание. Следует помнить, что прямыми методами также невозможно получить точное решение системы вследствие накопления погрешностей округления

Алгоритмы методов

и примеры их реализации в электронной таблице

Метод Гаусса (схема единственного деления)

Внести расширенную матрицу коэффициентов А, которая получается присоединением к матрице коэффициентов вектора правой части в качестве n+1 столбца.
Проверить, имеет ли матрица коэффициентов диагональное преобладание.
Прямой ход. Цель прямого хода – привести расширенную матрицу коэффициентов к треугольному виду, с единичными элементами на главной диагонали. Выполнить 1 шаг: для того, чтобы рассчитать первую строку матрицы А¹ , необходимо поделить первую строку матрицы А на диагональный элемент а₁₁.

j=1, n +1

Для того, чтобы рассчитать i- тую строку матрицы А¹, необходимо от i- той строки матрицы А отнять первую строку матрицы А¹, домноженную на элемент а_i1 матрицы А.

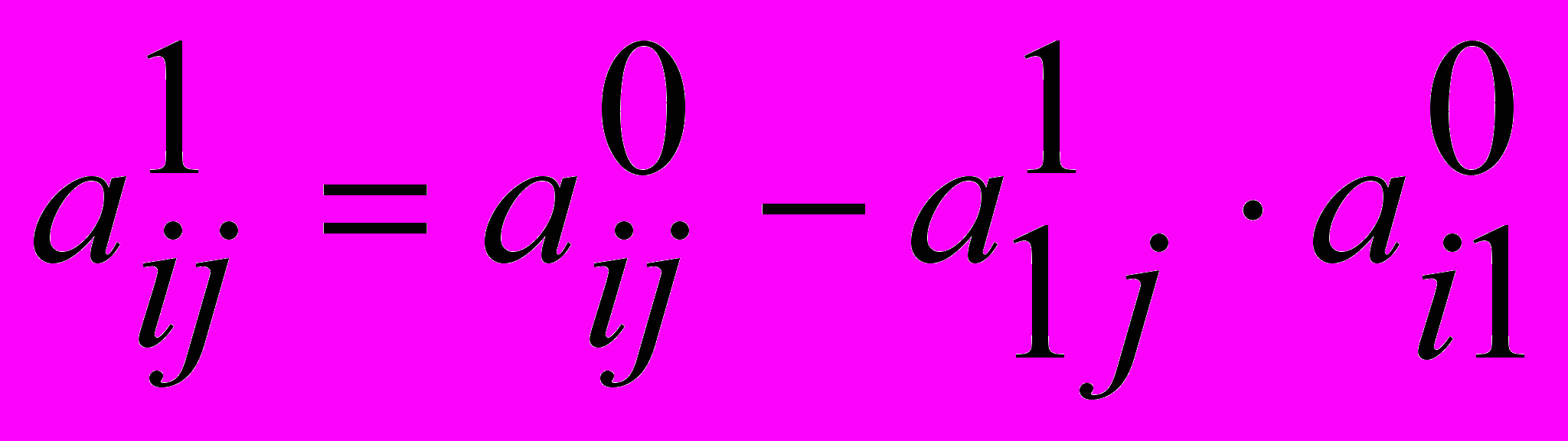, i = 2 , n j =1, n+1

После выполнения первого шага 1 столбец и 1 строка приведены к нужному виду.

Выполнить 2 шаг: выполняем те же действия с матрицей А¹, не трогая ее 1 строку и 1 столбец, т.е. работаем с матрицей порядка n-1.
После выполнения 2 шага имеем матрицу А², в которой 2 строка и 2 столбец приведены к нужному виду и т.д.
На каждом шаге m имеем

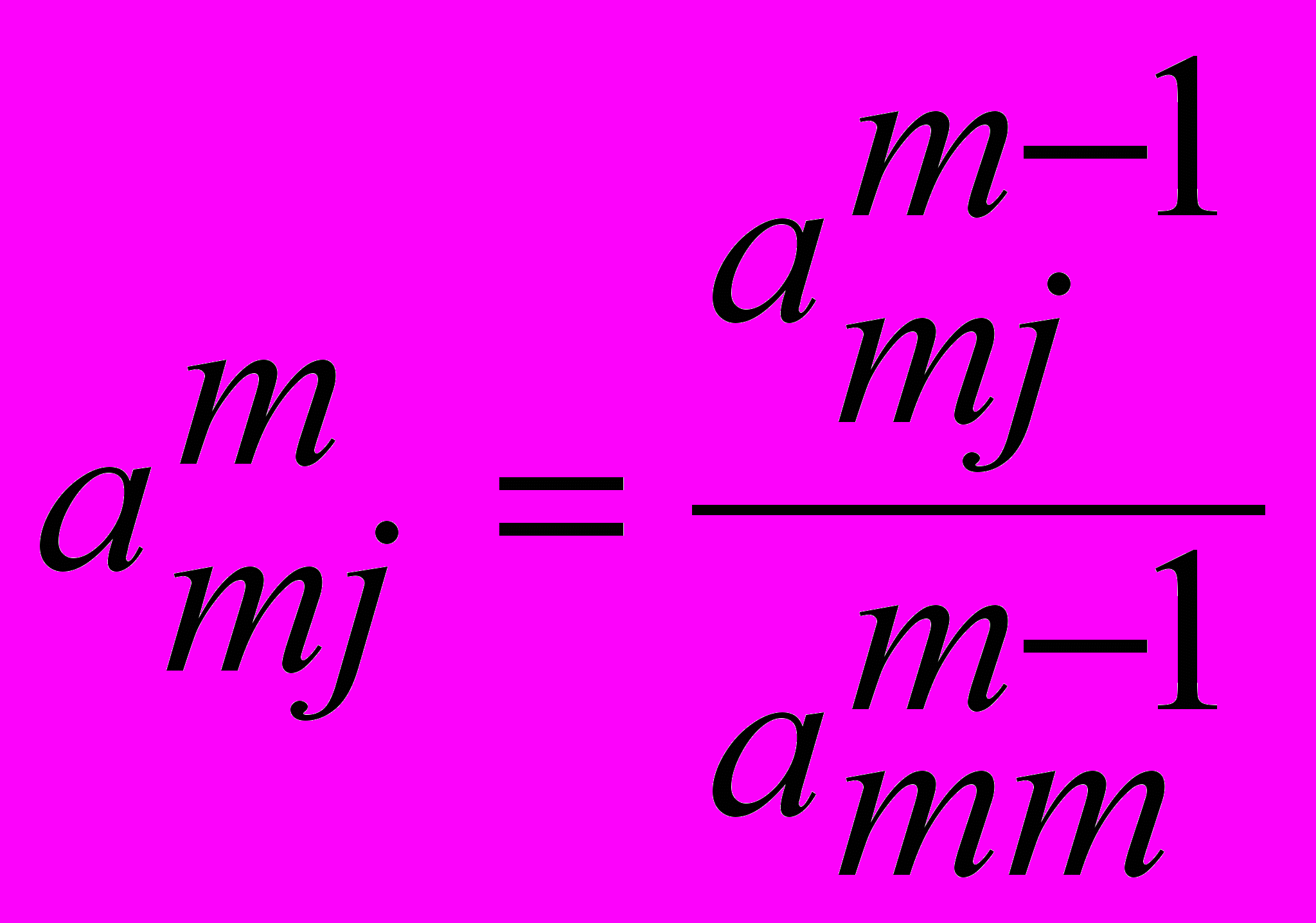, j = m, n+1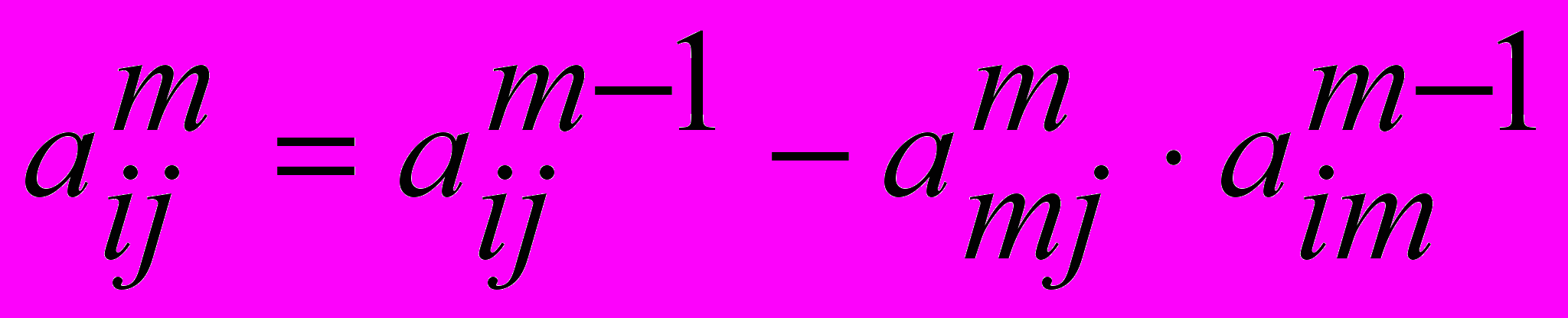

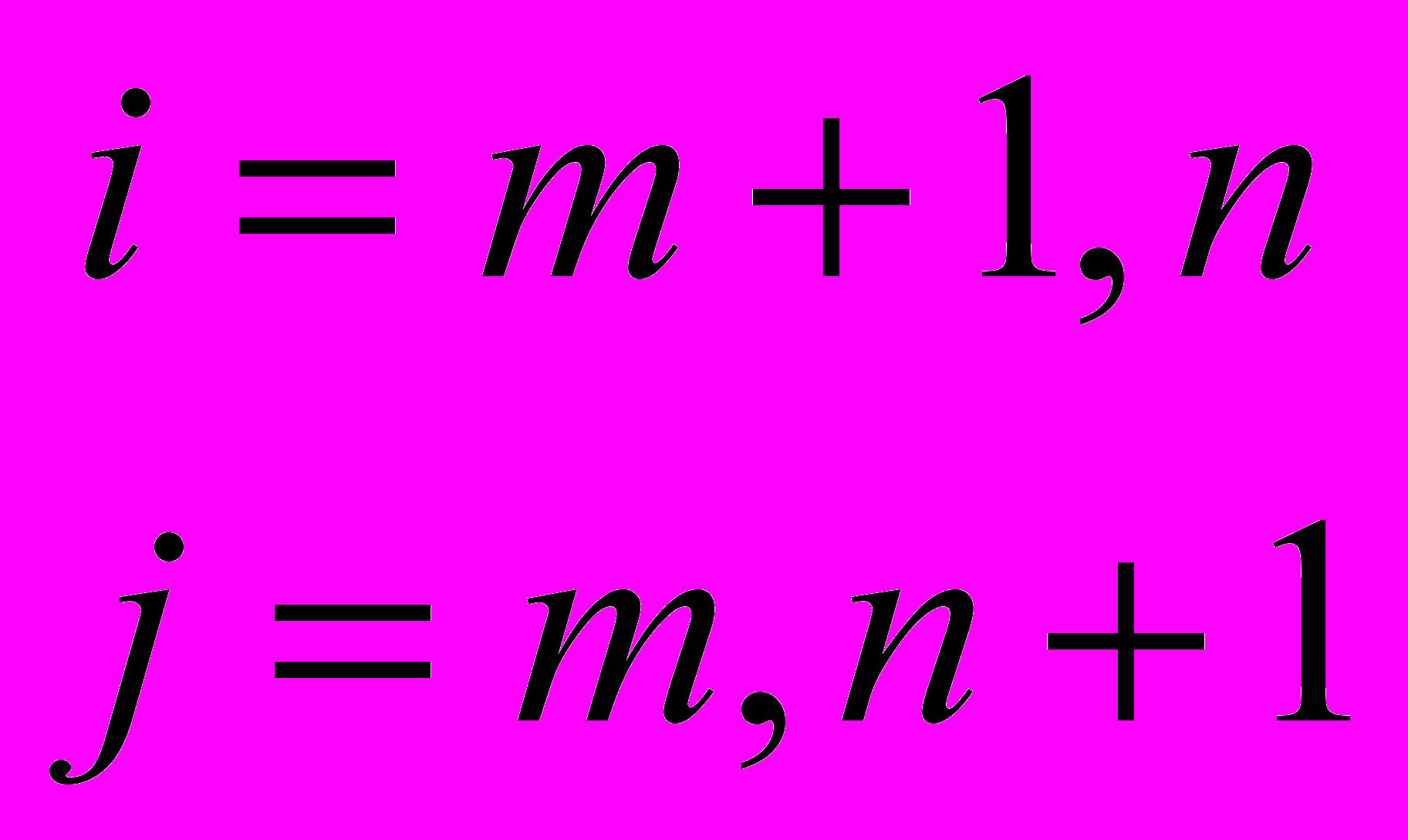
Количество шагов равно размеру матрицы m = 1,2,…n.
Обратный ход. Обратным ходом находим решение, начиная с x_n, с последней строки:

Выполняем проверку.

	A	B	C		D	E	F	G	H		I
1	Решение системы линейных уравнений методом Гаусса
2	A – матрица коэф.тов					F – вектор правой части				Проверка
3		3		2	1	6				6
4		2		5	2	9				9
5		1		1	3	5				5
6				Прямой ход
7	1 шаг	1		0,6667	0,3333	2
8		0		3,6667	1,3333	5
9		0		0,3333	2,6667	3
10
11	2 шаг			1	0,3636	1,3636
12				0	2,5455	2,5455
13
14	3 шаг				1	1
15				Обратный ход
16					x1	1
17					x2	1
18					x3	1

Примечание. Для того, чтобы выполнить проверку, нужно матрицу коэффициентов умножить на вектор найденного решения (с помощью функции МУМНОЖ), полученный вектор сравнить с вектором правой части.

Метод прогонки

(для решения систем с трехдиагональной матрицей коэффициентов)

1.Внести расширенную матрицу коэффициентов А, которая получается присоединением к матрице коэффициентов вектора правой части в качестве n+1 столбца.

2. Проверить, имеет ли матрица коэффициентов диагональное преобладание.

3. Для, того, чтобы было удобно пользоваться формулами метода, обозначить коэффициенты, стоящие под главной диагональю a_i i=2,3..n – номер строки, на главной диагонали – b_i, i=1,2…n, над главной диагональю – c_i, i=1,2…n-1, коэффициенты n+1 столбца – f_i i=1,2…n.

Прямой ход. Цель прямого хода – привести расширенную матрицу коэффициентов к треугольному виду, с единичными элементами на главной диагонали. Прямой ход выполняется в один шаг. Элементы новой матрицы коэффициентов рассчитываются по формулам:

элементы, стоящие над главной диагональю k_i, i=2,3…n

;

;

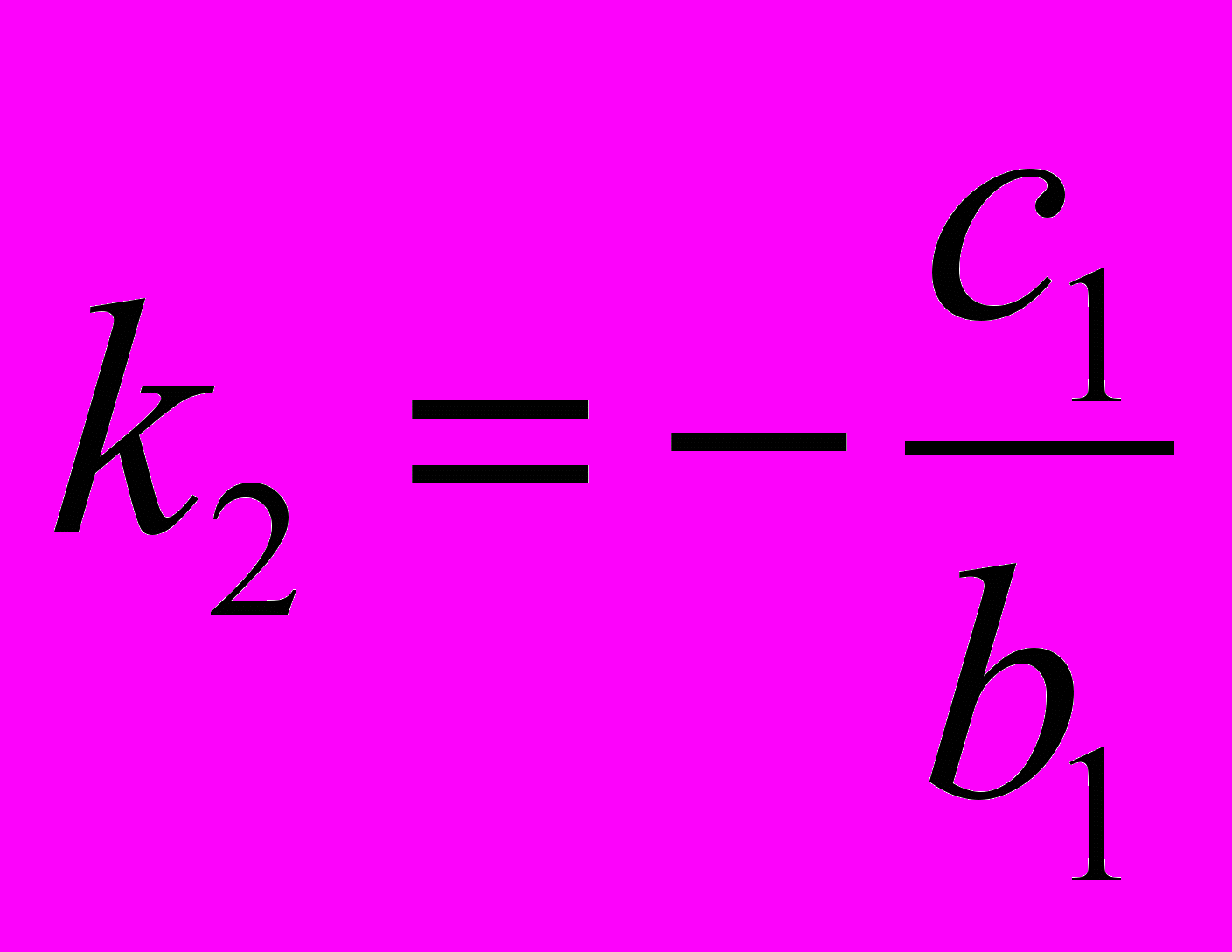элементы n+1 столбца, l_i, i=2,3…n+1

;

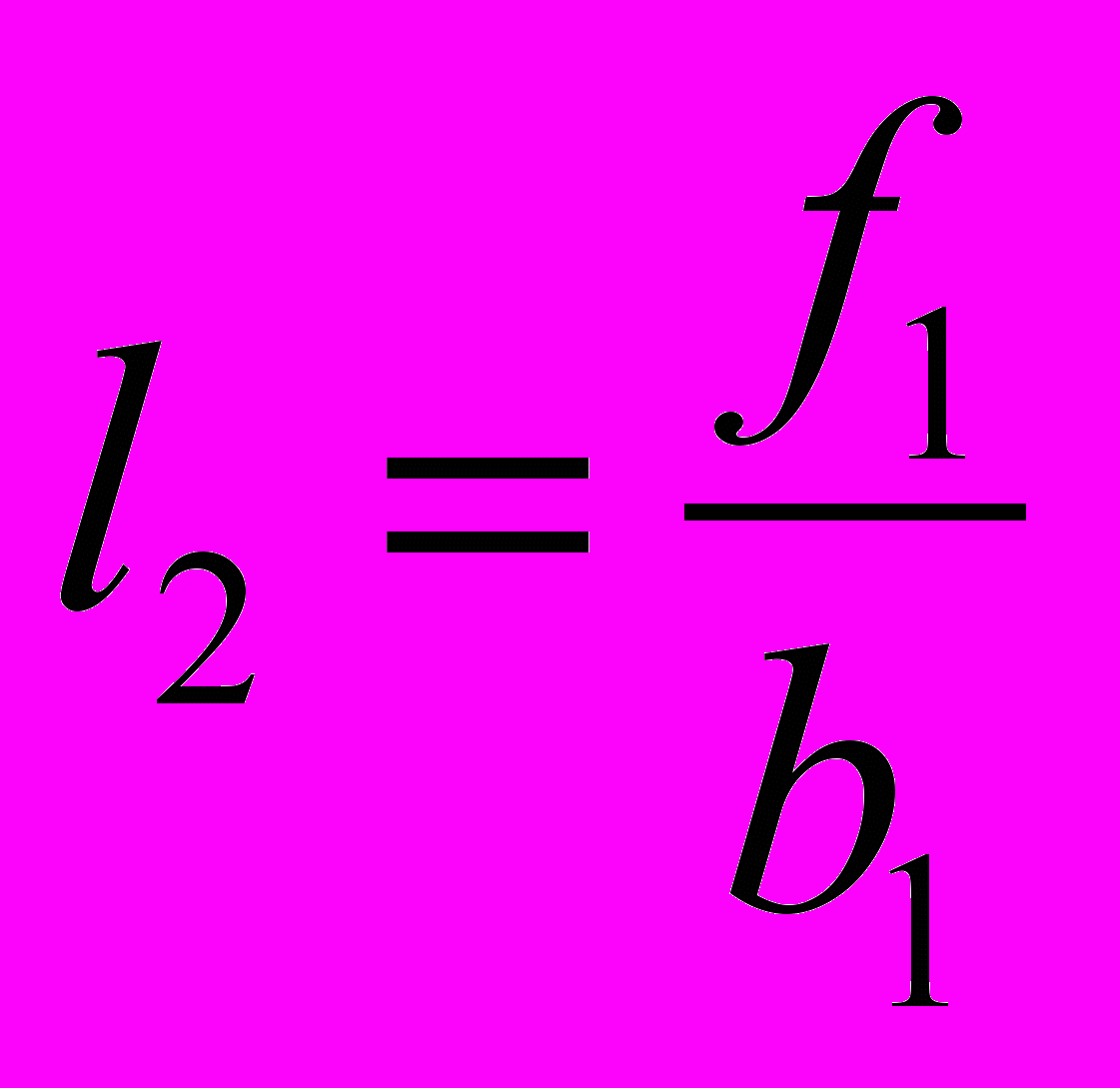Обратный ход. Обратным ходом находим решение, начиная с x_n, с последней строки:

;

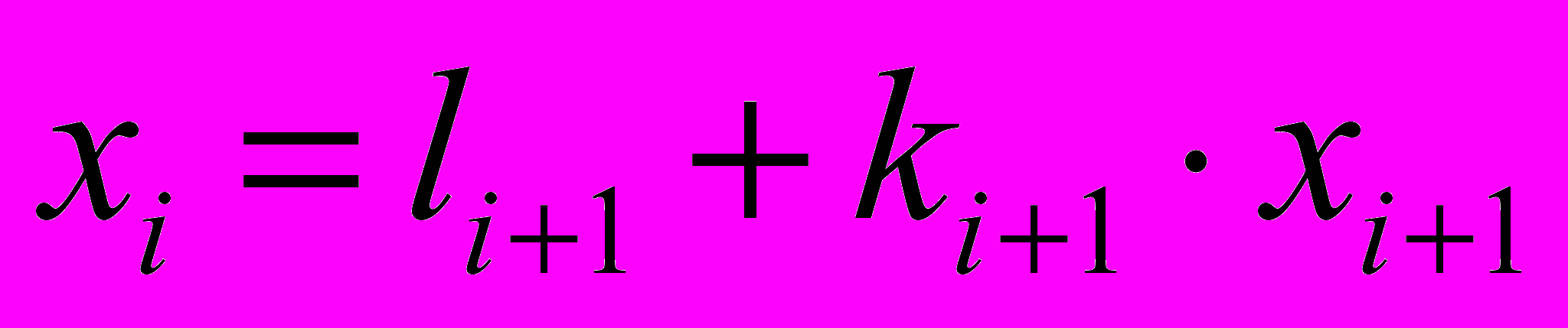i = n-1,n-2,…,1

Выполняем проверку.

	A	B	C		D	E	F	G	H		I
1	Решение системы линейных уравнений методом прогонки
2	A – матрица коэф.тов					F – вектор правой части				Проверка
3	3	2		0	0	5				5
4	2	5		2	0	9				9
5	0	1		3	1	5				5
6	0	0		2	4	6				6
7	Исходная матрица					Треугольная матрица				Обратный ход
8	i	a_i		b_i	c_i	f_i	k_i	l_i		x_i
9	1	*		3	2	5				1
10	2	2		5	2	9	-0,667	1,6667		1
11	3	1		3	1	5	-0,546	1,54546		1
12	4	2		4	*	6	-0,407	1,4074		1
13	5							1

Blog