Тема: «решение систем линейных алгебраических уравнений методом гаусса»

Вид материала

Решение

Содержание Теорема Кронеккера-Каппели. A. Условие detA

Подобный материал:

• Название читаемого курса, 134.62kb.
• Лекция № Тема 1: Системы линейных алгебраических уравнений. Метод Гаусса решения систем, 50.61kb.
• В. Н. Страхов новая теория регуляризации систем линейных алгебраических уравнений, 25.89kb.
• Программа решения системы линейных уравнений по методу Гаусса 7 2 Программа решения, 230.48kb.
• «Численные методы», 64.5kb.
• Решение систем линейных алгебраических уравнений методом прогонки, 112.31kb.
• Контрольная работа по курсу «Линейной алгебры и математического программирования», 99.84kb.
• Вопросы к экзамену 1 семестр, 56.89kb.
• Й в виде прямоугольной таблицы элементов кольца или поля, которая представляет собой, 71.89kb.
• Лекция №1. Тема 1: Системы линейных алгебраических уравнений. Метод Гаусса решения, 47.04kb.

Тема: «РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ ГАУССА»


В общем случае система n линейных уравнений для n неизвестных х_i имеет вид

a₁₁ x₁ + a₁₂ x₂ + . . . + a_1n x_n = b₁

a₂₁ x₁ + a₂₂ x₂ + . . . + a_2n x_n = b₂

. . . . . . . . . . . . . . . (1)

a_n1 x₁ + a_n2 x₂ + . . . + a_nn x_n = b_n


Из коэффициентов системы a_{i k} и свободных членов b_i построим основную матрицу системы ( А ) и расширенную матрицу (A/B)

A = 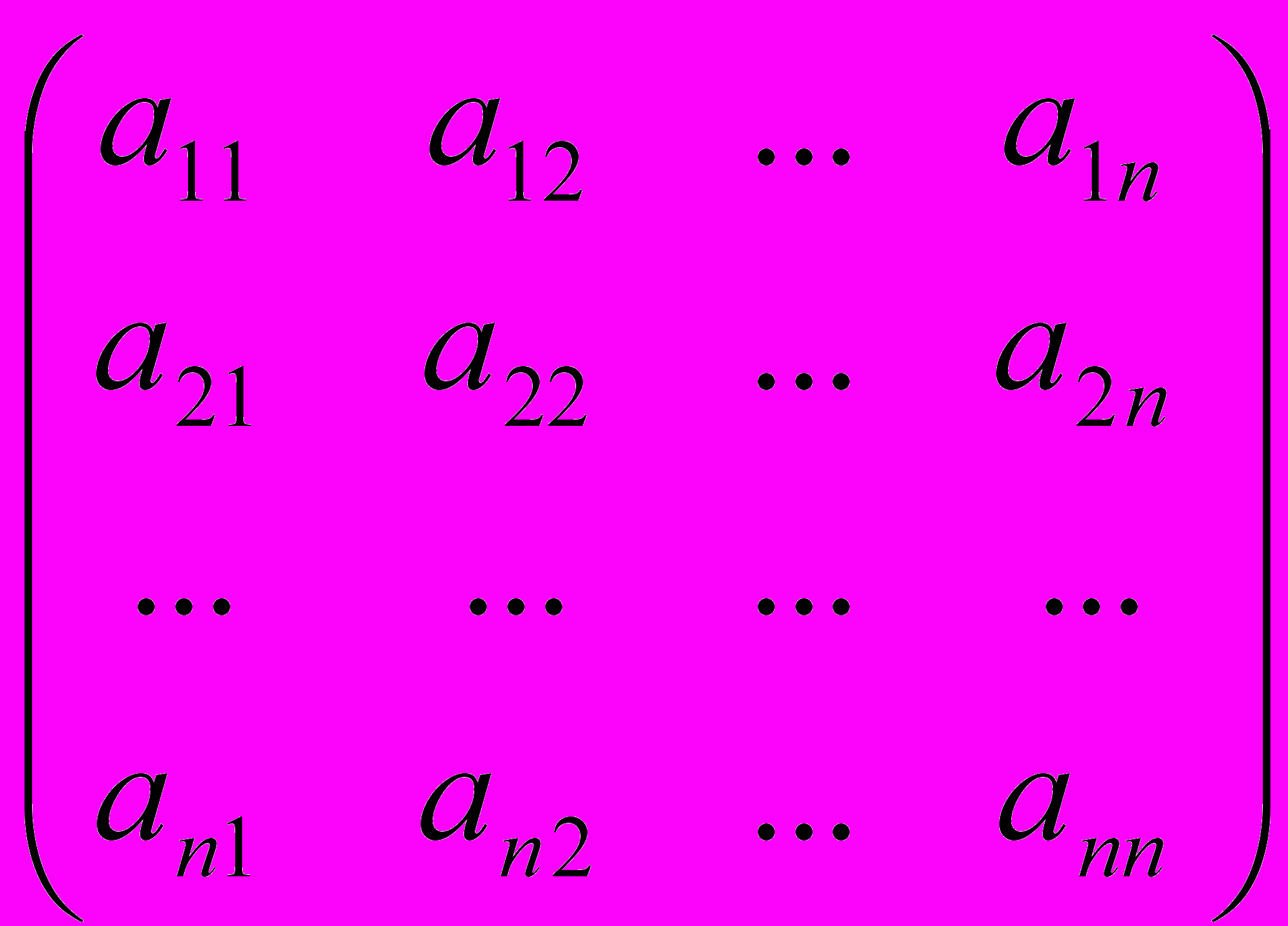(A/B) =

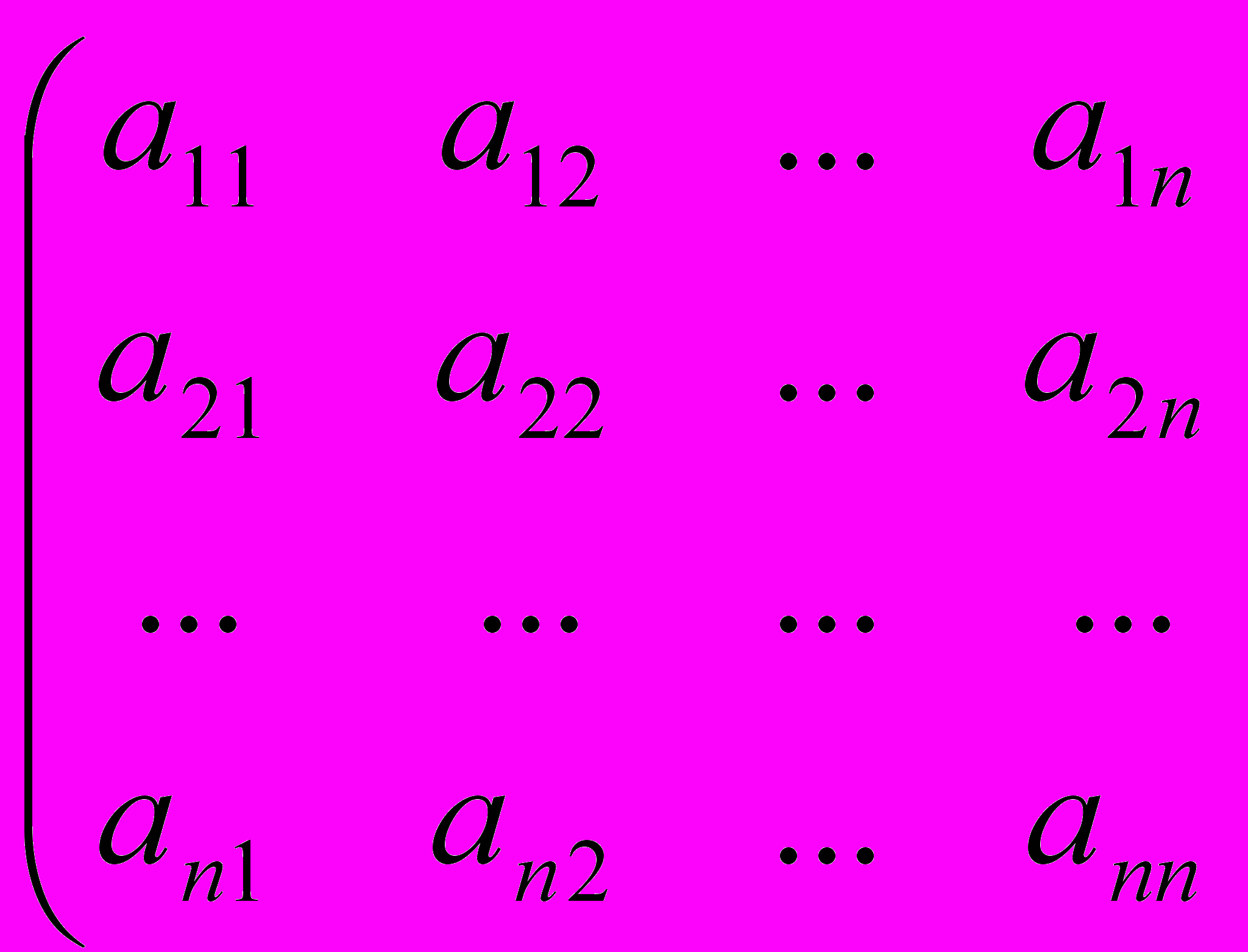
Решением системы линейных алгебраических уравнений (СЛАУ) наз. совокупность из n чисел x_i , которые обращают ее в верные равенства.

Две системы уравнений называются равносильными, если все их решения совпадают. СЛАУ переходит в равносильную при выполнении следующих преобразований: 1)уравнения меняются местами; 2)любое уравнение умножается на 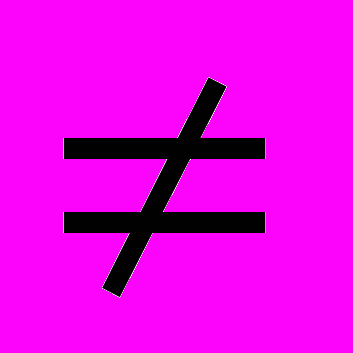0 ; 3) к обеим частям одного уравнения прибавляются соответствующие части другого, умноженные на произвольное число.

Каждое из уравнений системы накладывает определенное ограничение на возможные значения переменных х_i. В некоторых случаях эти ограничения могут противоречить друг другу или дублировать друг друга. В соответствии с этим все системы уравнений делятся на три типа:

а) совместные определенные - решение существует, причем, единственное

б) совместные неопределенные - существует бесконечное множество решений

в) несовместные - нет решений

Тип системы определяется наличием линейной зависимости между ее уравнениями.

Определение. Система уравнений линейно зависима, если хотя бы одно из уравнений можно представить как линейную комбинацию остальных уравнений системы.

Пример.

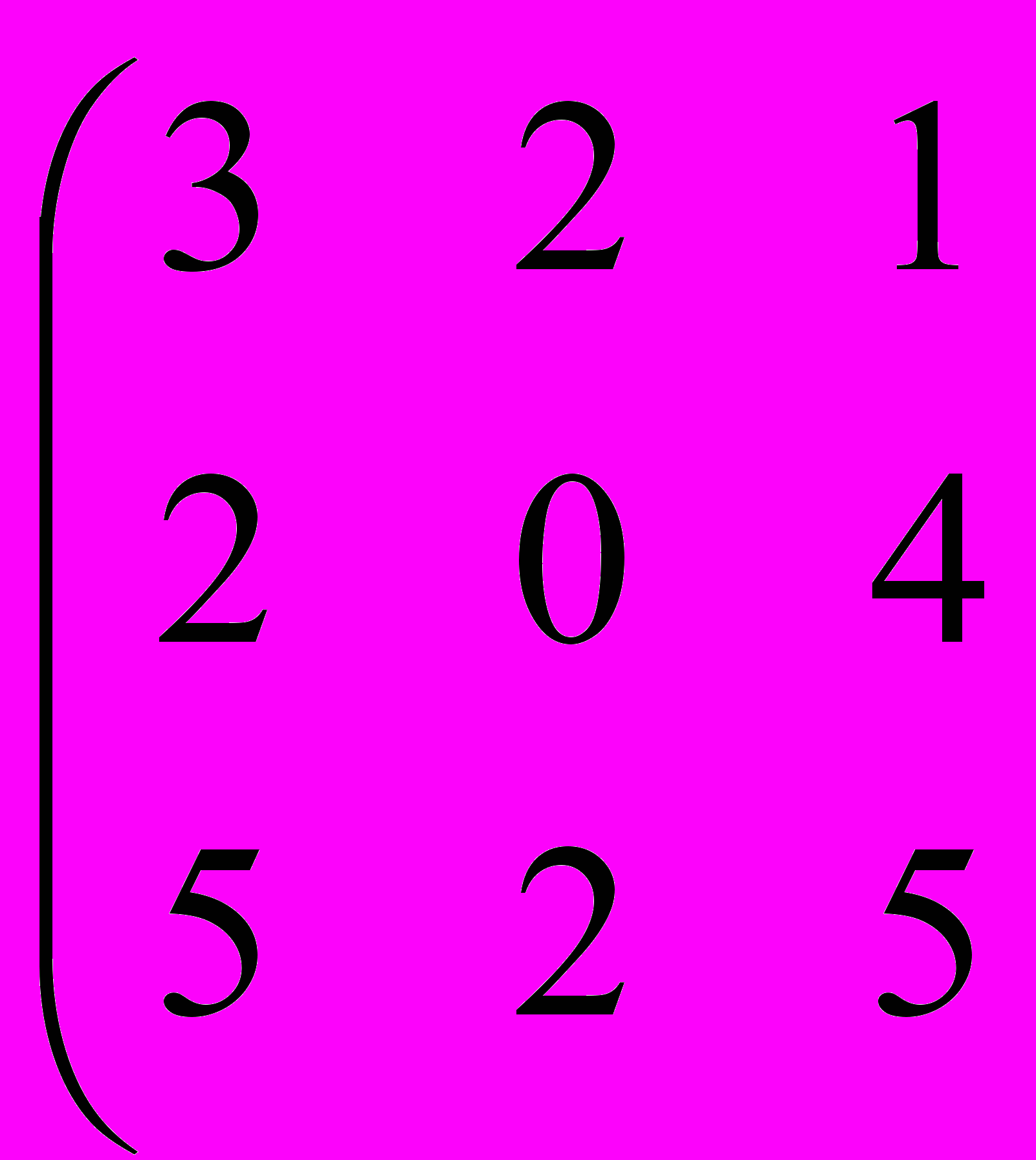
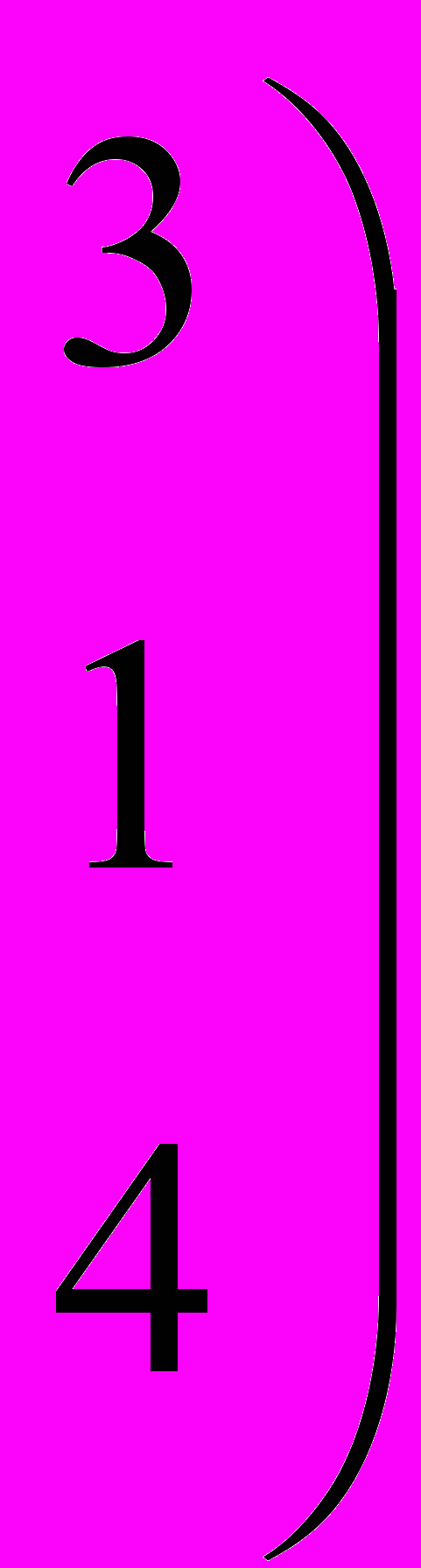
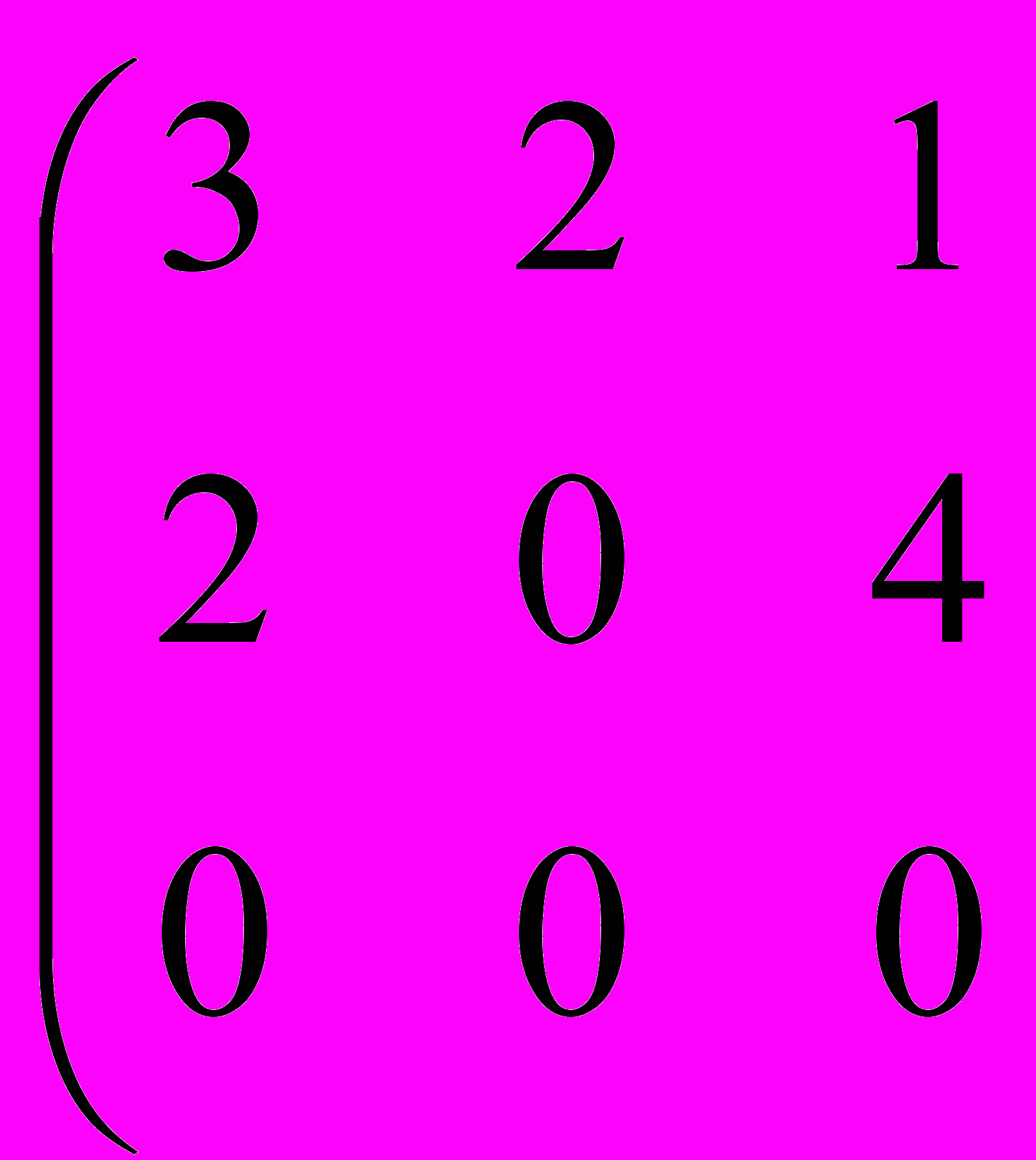
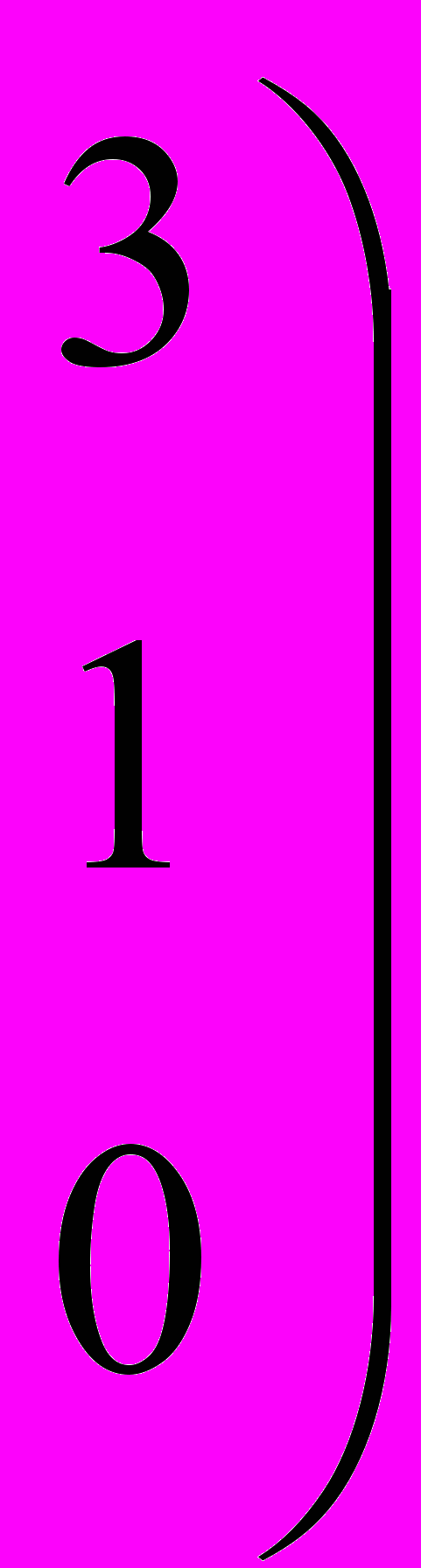
Здесь 3-е уравнение есть сумма 1-ого и 2-ого уравнения. Вычтем из 3-его уравнения 1-ое и 2-ое и получим нулевую строчку.

Для линейно зависимой системы уравнений всегда можно построить равносильную систему, в которой одно или несколько уравнений имеют нулевые коэффициенты. Тогда detA = 0, число уравнений меньше n и система оказывается недоопределенной. При этом, важно знать общее число линейно независимых строк. Условие detA = 0 означает, что левые части каких-то двух уравнений системы равны или пропорциональны друг другу. Если и свободные члены этих уравнений сохраняют туже пропорциональность, то имеем несколько полностью совпадающих уравнений. Если пропорциональность свободных членов другая, то уравнения оказываются несовместными, т.е. приводят к условию типа 2 = 3.


^ Теорема Кронеккера-Каппели. Система линейных алгебраических уравнений совместна, если ранги основной и расширенной матриц совпадают: rаngA = rаng(A/B).

Однородные СЛАУ всегда совместны, т.к. дополнительный столбик из 0 не может изменить rаng^ A. Условие detA 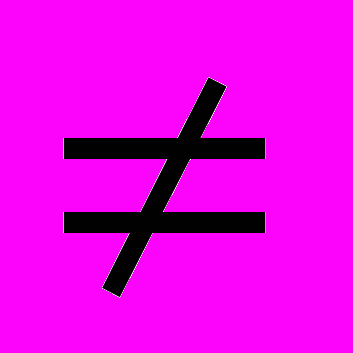0 означает, что все уравнения системы линейно независимы, rаngA = n, и система имеет единственное решение.

Таким образом, для определения типа решаемой системы уравнений достаточно знать значение detA, rаngA, rаng(A/B).


Метод Гаусса.

Основная идея: путем элементарных преобразований представить расширенную матрицу (А/В) системы уравнений ( 1 ) в треугольной форме, когда все элементы ниже главной диагонали обращены в нуль. В итоге получаем отдельные уравнения для каждого х_i , которые легко решаются.

(A/B) = 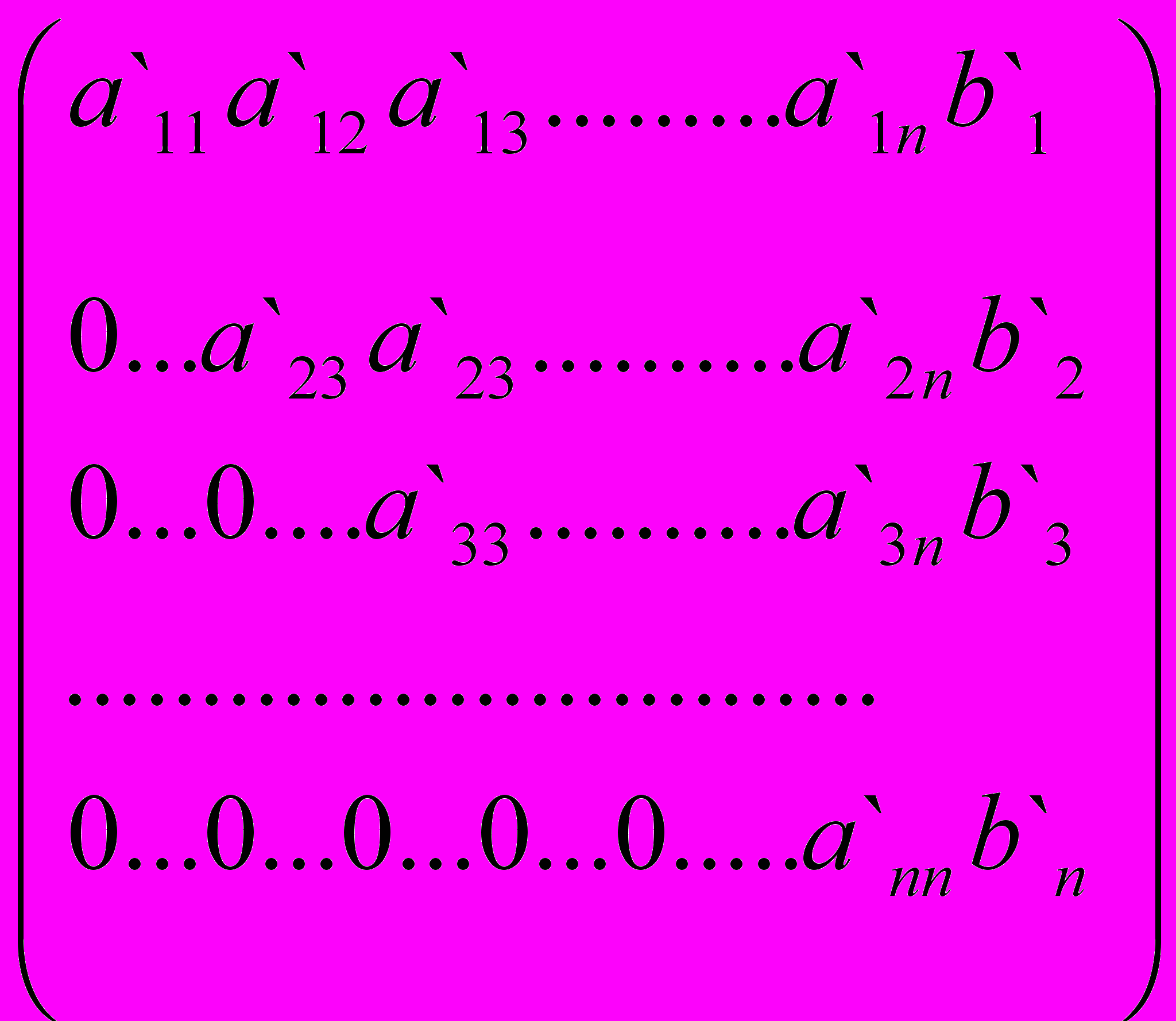( 2 )

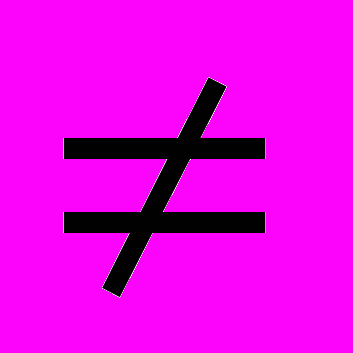где a`<sub>11</sub> 0 и a`_{i k} - значения переопределенных коэффициентов. Нули первого столбца получаются после последовательного умножения первого уравнения из ( 1 ) на - a₂₁/a₁₁ , - a₃₁/a₁₁ , . . . , -a_n1/a₁₁ и прибавления его к 2, 3, . . . n уравнению. Аналогично получаются остальные нули. Нижняя строка матрицы определяет уравнение

a`<sub>nn</sub> x<sub>n</sub> = b`_n ( 3 )

Возможны три случая:

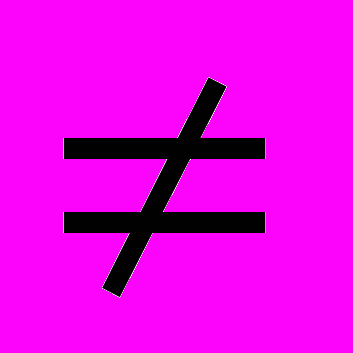1. a`<sub>nn</sub> 0 , тогда решение существует и единственно: х<sub>n</sub> = b`_n /a`_nn
   

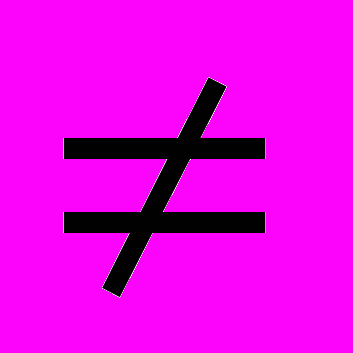2. a`<sub>nn</sub> = 0 и 0 х<sub>n</sub> = b`_n 0 , система не совместна, решений нет.

3. а`<sub>nn</sub> = 0 и 0 х<sub>n</sub> = b`_n = 0 , система совместна, бесконечное множество решений.

После решения уравнения (3) переходим к выше стоящему уравнению, заменяем в нем х_n на полученное число и приходим к линейному уравнению для х_n-1, решаем его и делаем переход к следующему уравнению и т.д.


Пример 1. x - 5y + 2z = 6 1-ю строку умножим на - 3 и прибавим ко 2-ой

3x - y - z = - 3 1-ю строку умножим на 2 и прибавим к 3-ей

-2x + 2y + 3z = 3 Затем, 2-ю строку умножим на 4 и прибавим к 3-ей





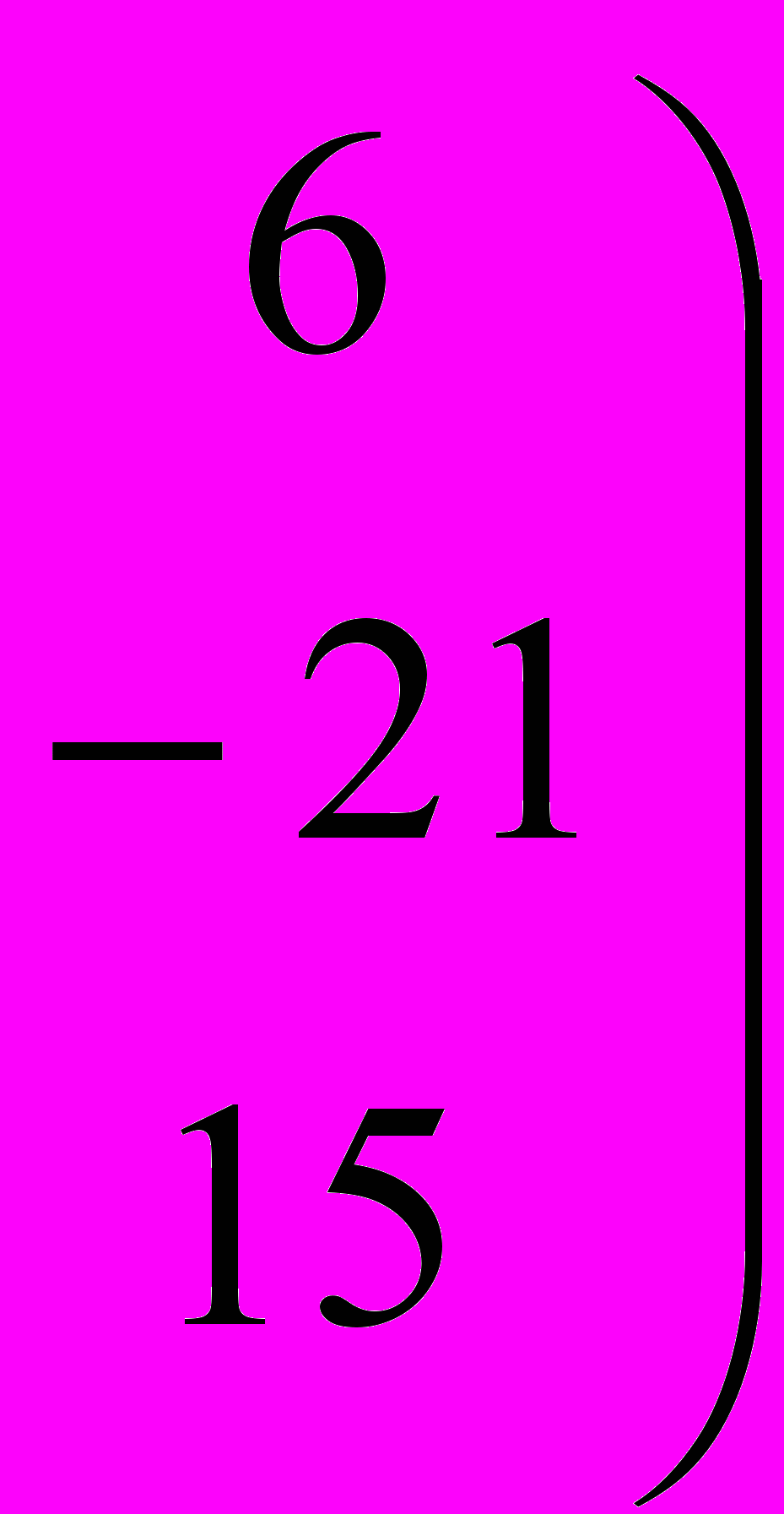
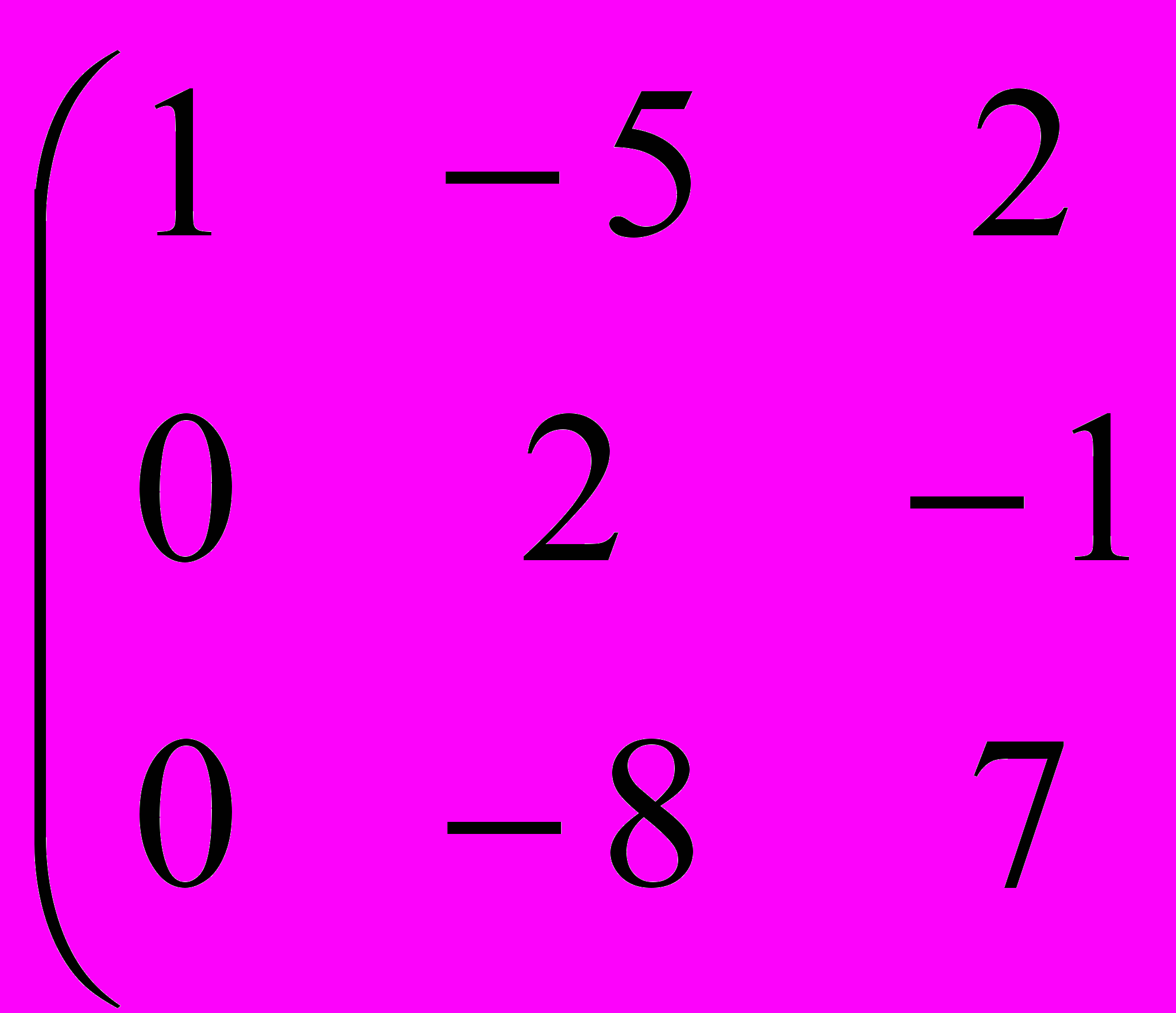
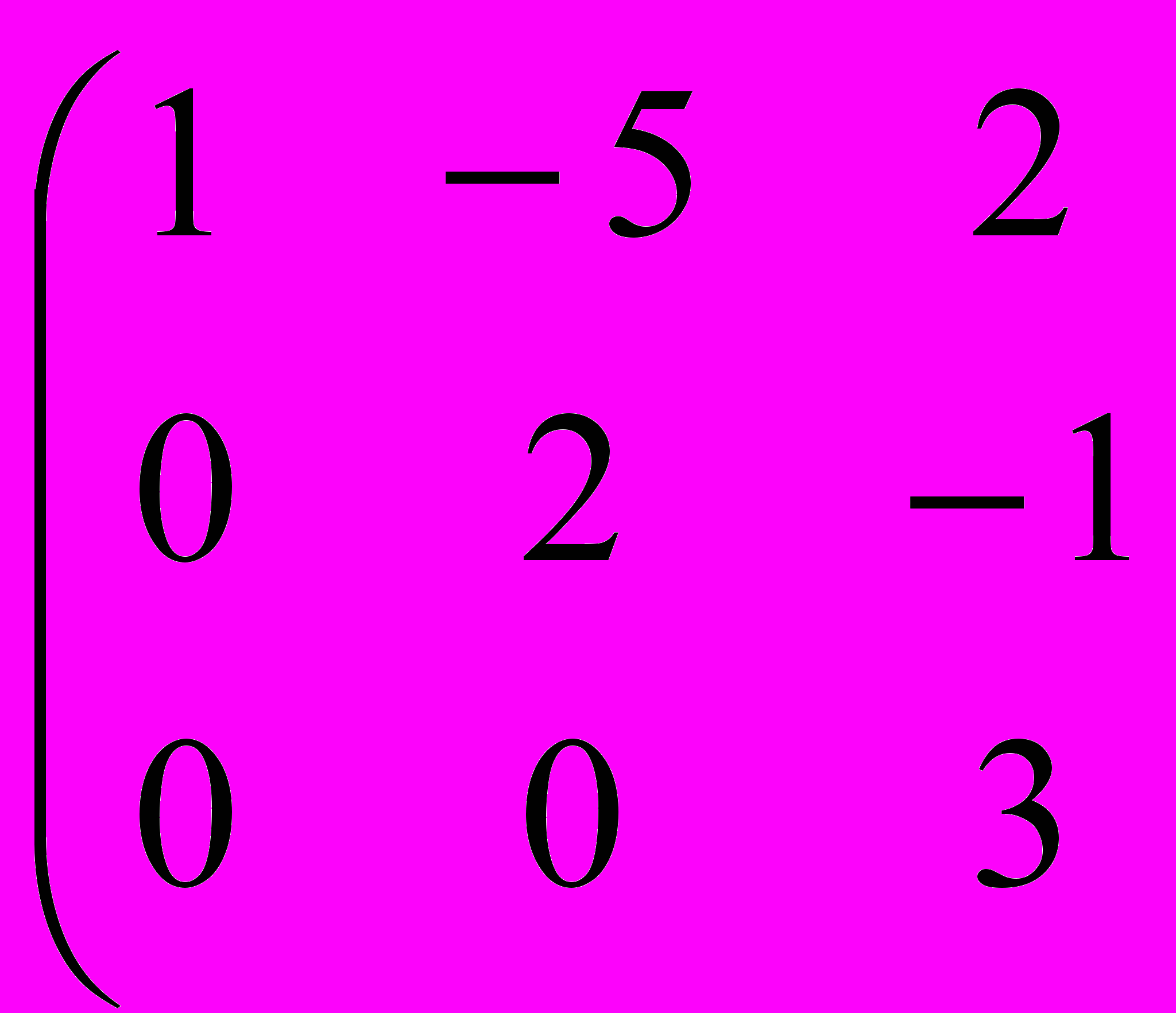
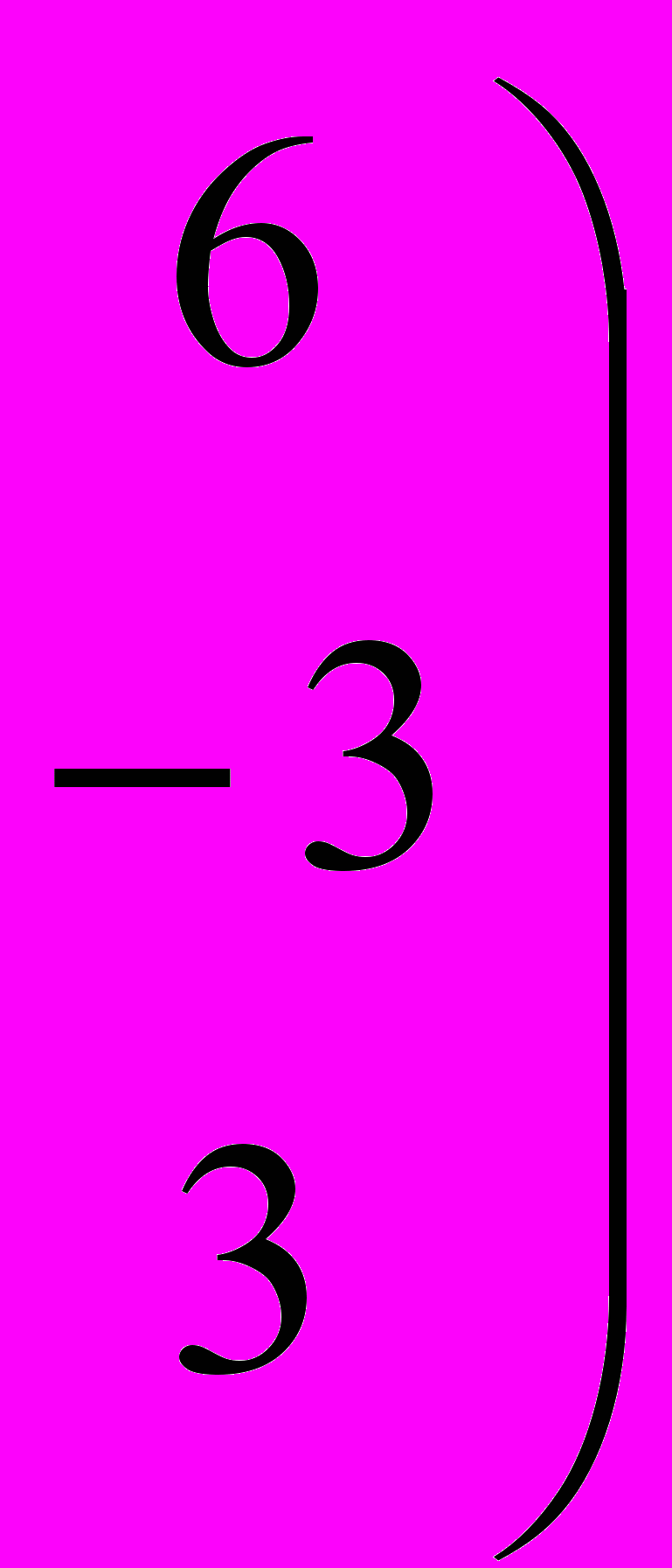
3 – е уравнение : 3z = 3 z = 1

2 – ое уравнение : 2y - z = -3 2y - 1 = -3 y = -1

1 – ое уравнение : x - 5y + 2z = 6 x + 5 + 2 = 6 x = -1


Пример 2. Исследовать систему уравнений на совместность и решить её методом Гаусса.

3x – y – z = –3

2x + 2y + 4z = 0

–x – 3y + z = 5

Преобразуем расширенную матрицу системы уравнений к треугольному виду

(A/B) = = =

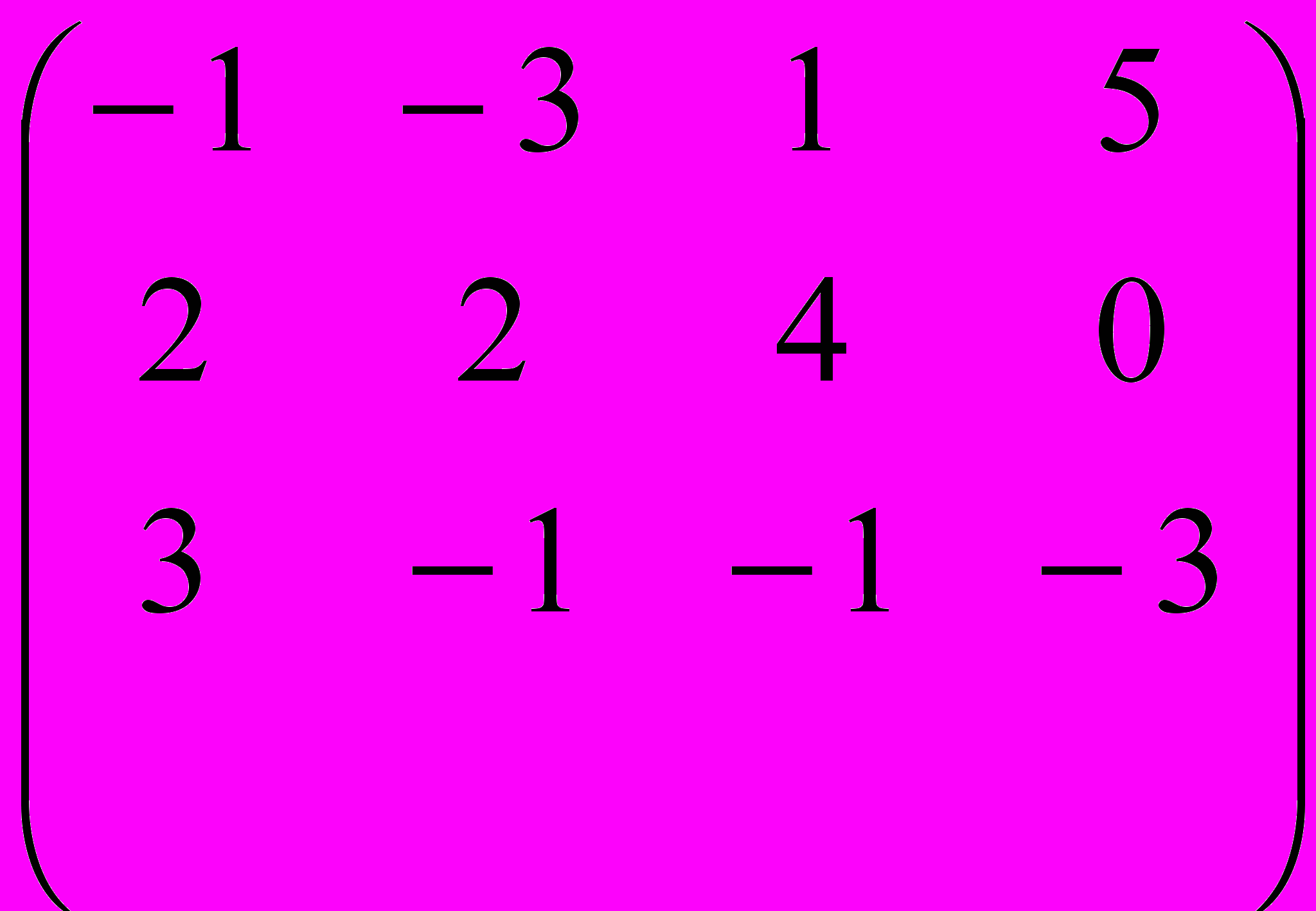
Поменяли порядок строк. Первую строку умножили на 2 и прибавили ко второй. Первую строку умножили на 3 и прибавили к третьей.

= = .

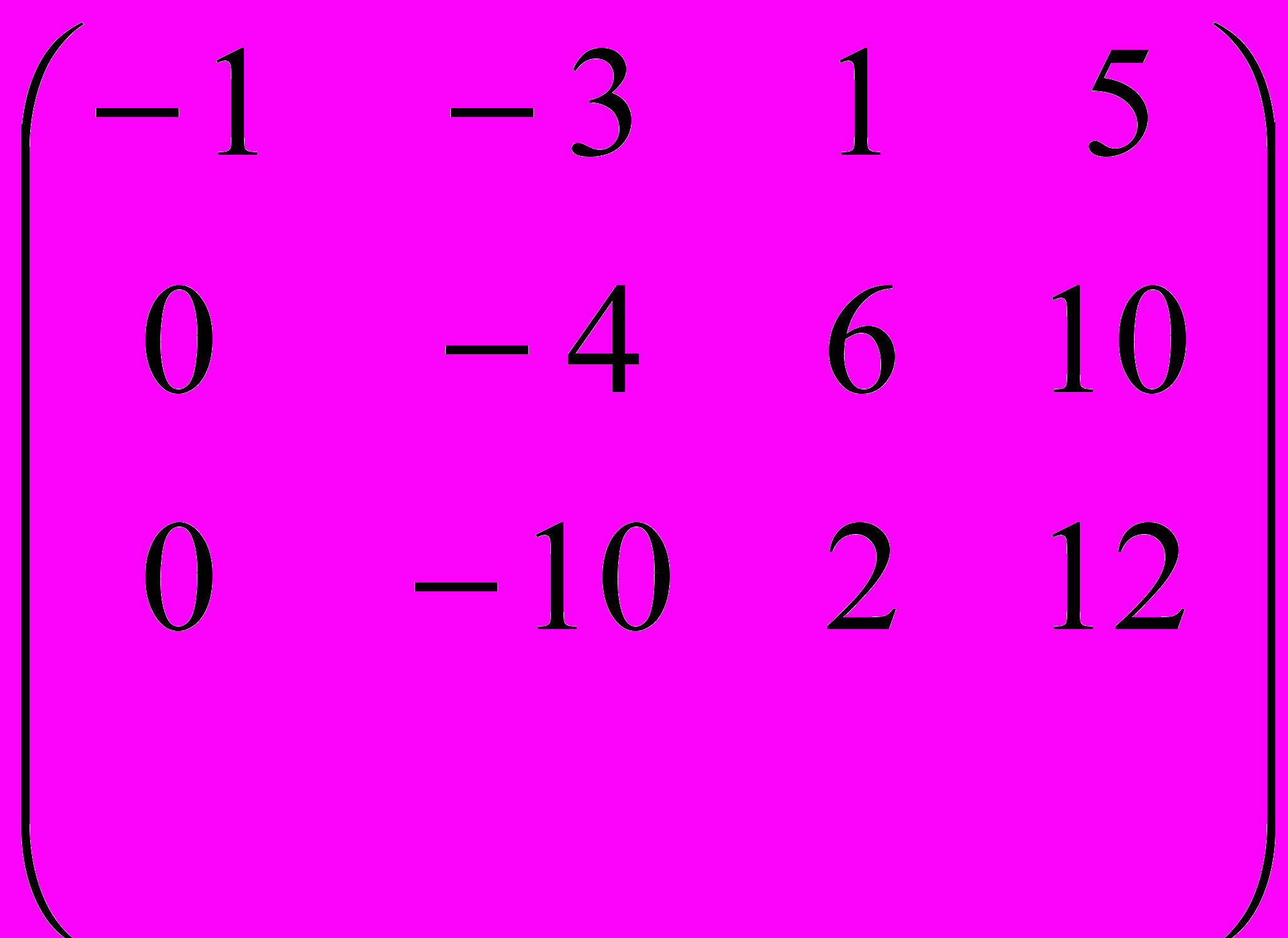
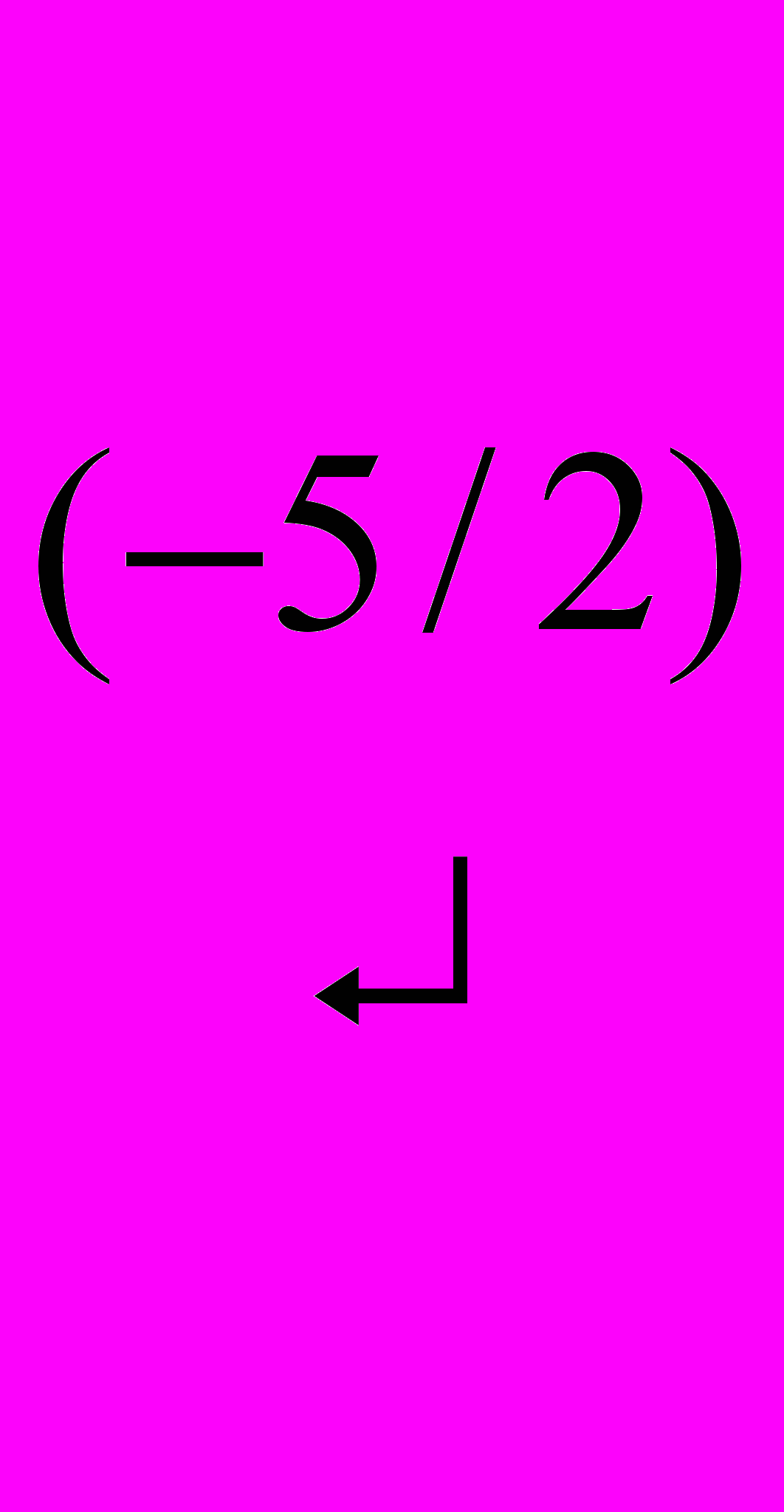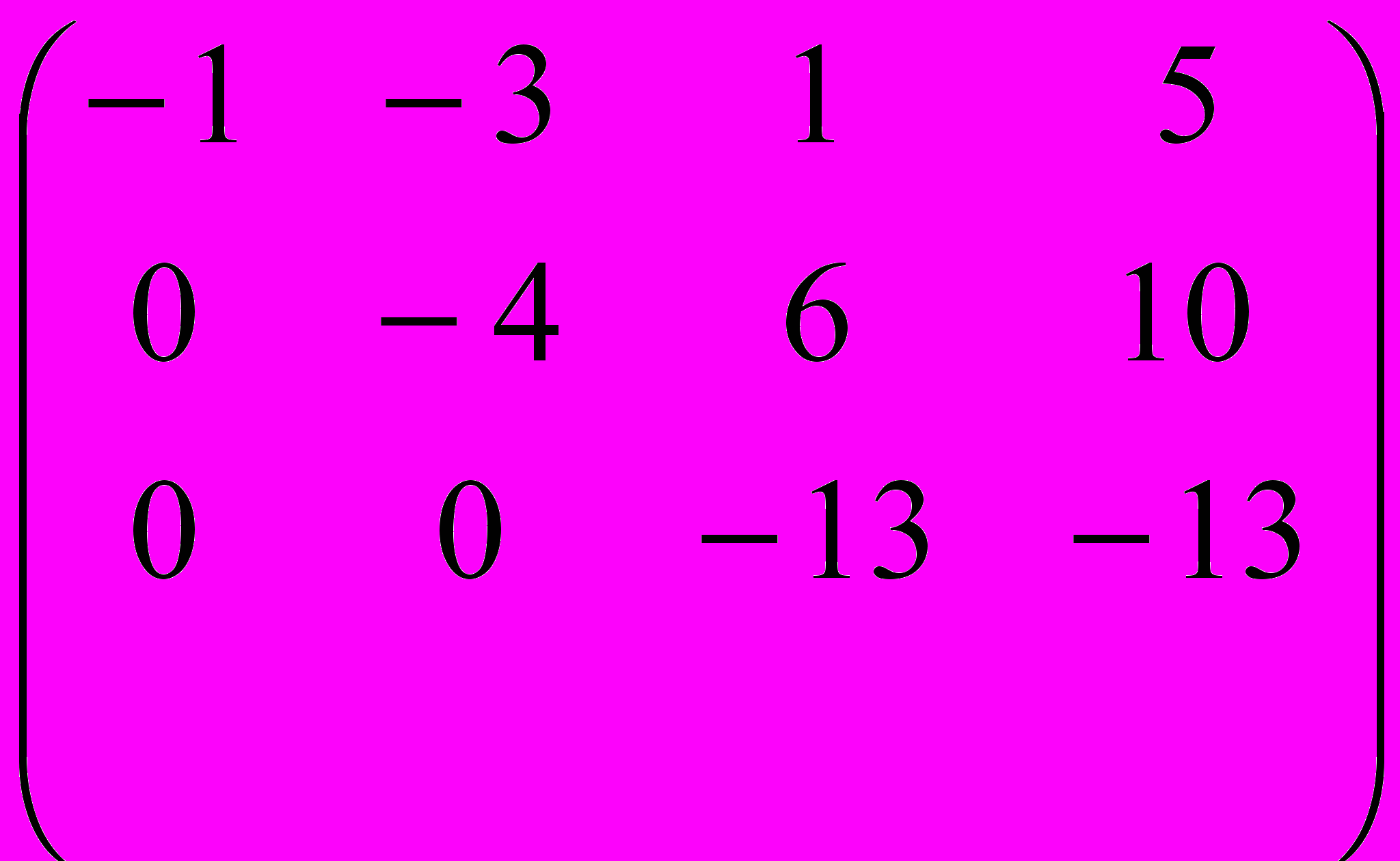Вторую строку умножили на –5/2 и прибавили к третьей. Пришли к треугольной форме матрицы, из которой следует:

3 строка определяет уравнение –13Z = –13 Z = 1

2 строка определяет уравнение –4Y + 6Z = 10 –4Y = 4 Y = –1

1 строка определяет уравнение –X – 3Y + Z = 5 –X = 1 X = –1


Ответ: X = –1, Y = –1, Z = 1.