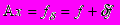В. Н. Страхов новая теория регуляризации систем линейных алгебраических уравнений с приближенными данными большой и сверхбольшой размерности курс лекций

Вид материала

Курс лекций

Подобный материал:

• Вопросы к экзамену 1 семестр, 56.89kb.
• Й в виде прямоугольной таблицы элементов кольца или поля, которая представляет собой, 71.89kb.
• Лекция № Тема 1: Системы линейных алгебраических уравнений. Метод Гаусса решения систем, 50.61kb.
• Контрольная работа по линейной алгебре и аналитической геометрии «Системы линейных, 383.4kb.
• Лабораторная работа, 155.79kb.
• Вопросы к экзамену по курсу «Высшая математика часть, 14.58kb.
• Название читаемого курса, 134.62kb.
• Решение систем линейных алгебраических уравнений методом прогонки, 112.31kb.
• Урок в 7 классе по теме: «Системы линейных уравнений в решении алгебраических задач», 97.42kb.
• Тема: «теория матриц» Основная задача линейной алгебры, 28.88kb.

Академик В.Н.Страхов


НОВАЯ ТЕОРИЯ РЕГУЛЯРИЗАЦИИ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С ПРИБЛИЖЕННЫМИ ДАННЫМИ –

БОЛЬШОЙ И СВЕРХБОЛЬШОЙ РАЗМЕРНОСТИ

(Курс лекций)


Основные линейные некорректные задачи геофизики – это задачи нахождения устойчивых приближенных решений систем линейных алгебраических уравнений (СЛАУ) вида

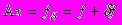(1)

и

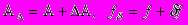. (2)

При этом типичными являются ситуации, когда:

1) СЛАУ (1)–(2) имеют большую,

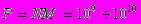(3)

или даже сверхбольшую

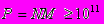(4)

размерность;

2) величины

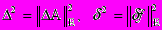(5)

неизвестны;

3) зато известны качественные свойства векторов 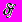и 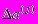, , 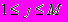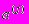суть векторы-столбцы матрицы А, а именно – что эти векторы являются случайными и однородными.

В курсе лекций описываются:

а) общая методология нахождения устойчивых приближенных решений подобного рода СЛАУ;

б) целый ряд принципиально новых методов нахождения устойчивых приближенных решений СЛАУ (1)–(2);

в) необходимость “сдать в архив” господствующие в настоящее время парадигмы в теории линейных некорректных задач, в вычислительной линейной алгебре, в вычислительной математической физике;

г) сущность новых парадигм в указанных областях вычислительной математики.


Лекция 1

Принципиально новая теория интерпретации потенциальных полей, центральная вычислительная проблема которой – нахождение устойчивых приближенных решений СЛАУ большой и сверхбольшой размерности.


Лекция 2

Классическая теория регуляризации СЛАУ и ее недостатки (и прежде всего – неадекватность потребностям и условиям геофизической практики).


Лекция 3

“Геофизический диалект” языка математики и его концептуальные установки.


Лекция 4

Априорная информация о векторах f, 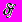и x в СЛАУ 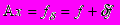и следствия из нее. Основные стратегии нахождения вектора .


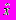Лекция 5

Новые ортогональные преобразования матриц.


Лекция 6

Универсальные методы нахождения .


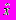Лекция 7

Принципиально новые итерационные методы нахождения .


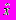Лекция 8

Новые экстремальные принципы в задаче нахождения .


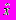Лекция 9

Подход к нахождению 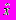, основанный на фильтрации заданного вектора .


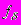Лекция 10

Новая парадигма вычислительной линейной алгебры.


Лекция 11

Новая парадигма вычислительной математической физики.


Лекция 12

Проблема создания лайнпьтеров. Заключительные соображения о новой парадигме регуляризации СЛАУ