Климов Валерий Николаевич, доцент кафедры математики рабочая программа
| Вид материала | Рабочая программа |
- Рабочая программа курса Практикум на ЭВМ. Специальность 510200, Прикладная математика, 87.68kb.
- Люсов Валерий Николаевич, к э. н., доцент, кафедры «Мировая экономика» учебно-методический, 2118.09kb.
- М. К. Аммосова рабочая программа курса Математика и информатика Специальность, 020700, 283.67kb.
- Климов Иван Павлович, доктор исторических наук, профессор кафедры, Романчук Иван Сергеевич,, 896.39kb.
- Рабочая учебная программа по дисциплине «Теоретические основы школьного курса математики», 316.89kb.
- Программа факультативных занятий для учащихся 6 класса общеобразовательных учреждений, 76.17kb.
- Рузаков Виталий Яковлевич, доцент кафедры математики рабочая программа, 120.18kb.
- Миков Юрий Вендимианович, доцент, к филос н., доцент каф теоретической и прикладной, 695.85kb.
- Шапко Ирина Валерьевна, к филос н., доцент кафедры Типс рабочая программа, 299kb.
- Липухин Дмитрий Николаевич рабочая программа, 249.02kb.
Федеральное агентство по образованию
ГОУ ВПО
«Уральский государственный горный университет»
УТВЕРЖДАЮ Председатель Методической комиссии
Института геологии и геофизики
__________________ Тагильцев С. Н.
«_____» _______________ 2008 г.
РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ
ЕН.Ф.01.01 – Алгебра и аналитическая геометрия.
Закреплена за кафедрой: математики.
Учебный план специальности подготовки дипломированных специалистов 230401(073000) – «Прикладная математика (ПМ)»
Часов по РУП: общая - 360 ч., обязат. , ауд. зан. - 240 ч., самостоятельная работа студентов – 120 ч.
Виды контроля в семестрах: экзамен в 1 и 2 семестрах.
Программу составил:
Климов Валерий Николаевич, доцент кафедры математики.
Рабочая программа дисциплины ЕН.Ф.01.01 – «Алгебра и аналитическая геометрия» составлена на основании:
а) государственного образовательного стандарта ВПО направления подготовки дипломированных специалистов 230400 (657100) – «Прикладная математика» (рег. номер 322 тех/ дс утв. 05.04.2000 г.);
б) учебного плана специальности 230401(073000) – «Прикладная математика (ПМ)» (утв. 20.10.2000 г.).
Рабочая программа одобрена на заседании кафедры математики.
Протокол № 21 от 26 сентября 2007 г.
Зав. кафедрой ________________ проф. Сурнев В. Б.
^ ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ
Целью изучения дисциплины «Алгебра и аналитическая геометрия» является формирование у студентов базовых знаний по алгебре и многомерной аналитической геометрии достаточных для освоения базовой программы 230402.
- ^ ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ СОДЕРЖАНИЯ ДИСЦИПЛИНЫ
Студент должен иметь представление:
- о теории множеств;
- об алгебраических операциях и отношениях на множествах;
- об основных алгебраических системах (группоид, полугруппа, группа, кольцо, поле, алгебра, векторное пространство);
- об основных числовых полях (поле действительных чисел, поле комплексных чисел);
- о кольце многочленов от одного неизвестного (действия с многочленами, делимость и корни многочленов, рациональные дроби);
- о векторных пространствах, операторах, матрицах, определителях и системах линейных алгебраических уравнений;
-о собственных подпространствах и характеристическом многочлене линейного оператора;
- о квадратичных формах и поверхностях второго порядка;
- о параметрическом задании поверхностей в пространстве
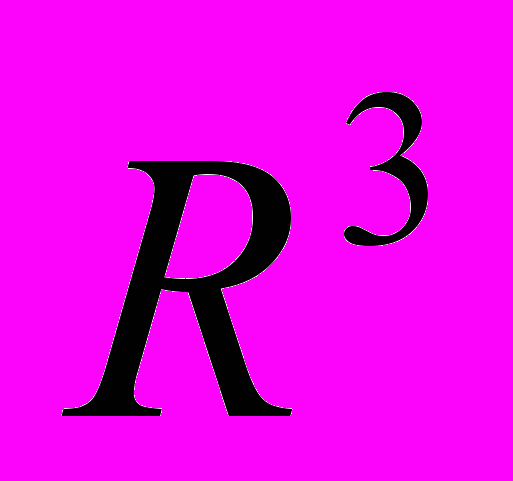 ;
;- о задании поверхностей неявными уравнениями;
- о векторных и тензорных полях в евклидовых пространствах.
^ Студент должен знать и уметь:
- основные факты из теории множеств;
- основные понятия теории алгебраических систем;
- основные факты из теории многочленов;
- основные факты из теории векторных пространств и операторов;
- основные методы исследования систем линейных и алгебраических уравнений;
- основные определения и факты из теории метрических и векторных нормированных пространств;
- основные понятия теории отображений;
- основные способы задания поверхностей;
- основные определения и теоремы тензорной алгебры;
- находить корни многочленов;
- раскладывать правильные рациональные дроби на простейшие дроби;
- уметь производить операции с векторами в векторных пространствах;
- основные методы решения и уметь решать системы линейных алгебраических уравнений;
- находить собственные значения и собственные векторы линейных операторов в конечномерных векторных пространствах;
- приводить квадратичные формы к каноническому виду;
- исследовать множества точек пространства
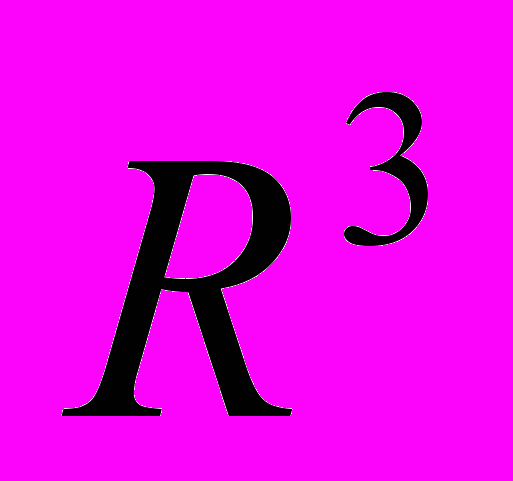 ;
;- исследовать поверхности по их уравнениям;
- производить преобразования с тензорными величинами.
^ Студент должен иметь навыки:
- исследования основных алгебраических систем;
- решения основных задач теории многочленов;
- решения основных задач линейной алгебры и аналитической геометрии;
- исследования и решения систем линейных алгебраических уравнений;
- исследования поверхностей в трехмерном пространстве;
- в выполнении основных операций тензорной алгебры в евклидовом пространстве.
^ 3. CОДЕРЖАНИЕ ДИСЦИПЛИНЫ (тематический план)
| Тема | Часы | ||
| лекции | пр.зан. | всего | |
| 1 семестр | |||
| 1. Введение в общую алгебру | 10 | 6 | 16 |
| 2. Линейные (векторные) пространства | 35 | 34 | 69 |
| 3. Линейные отображения и линейные преобразования n мерного векторного пространства | 13 | 8 | 21 |
| 4. Линейные подпространства | 9 | 6 | 15 |
| ^ Итого в 1 семестре: | 67 | 54 | 121 |
| 2 семестр | |||
| 5. Структура линейного преобразования | 18 | 16 | 34 |
| 6. Евклидовы n-мерные векторные пространства | 18 | 8 | 26 |
| 7. Геометрия многомерных пространств | 21 | 12 | 33 |
| 8. Основы тензорной алгебры | 18 | 8 | 26 |
| ^ Итого во 2 семестре: | 75 | 44 | 119 |
| ВСЕГО: | 142 | 98 | 240 |
1 семестр (67 ч.)
| ^ НАИМЕНОВАНИЕ РАЗДЕЛА И ТЕМЫ | Обязат. ауд. занятий ч. | ЛИТЕРАТУРА (страницы) |
| ЛЕКЦИИ | | |
| ^ I. Введение в общую алгебру (10 ч.) | | |
| 1. Элементы теории множеств: понятие множества, отношения между элементами и множествами; операции над множествами. Отношения на множествах; бинарное отношение, отношение эквивалентности, отношение порядка. | 2 ч. | [1] с.18-34,40-43 |
| ^ 2. Алгебраические системы: понятие n-арной алгебраической операции; бинарная, унарная и нульарная операции; множества с одной алгебраической операцией, понятие группы; множества с двумя алгебраическими операциями, понятие кольца и поля. | 1 ч. | [1] с.34-39,44-53 |
| ^ 3. Поле действительных чисел: аксиомы сложения действительных чисел; аксиомы умножения действительных чисел; дистрибутивные законы; аксиомы порядка множества действительных чисел; абсолютная величина действительного числа. | 1 ч. | [1] с.53-58 |
| ^ 4. Поле комплексных чисел: аксасматическое построение и теорема существования поля комплексных чисел; алгебраическая форма комплексных чисел; геометрическая интерпретация и тригонометрическая форма комплексных чисел; свойства сопряженных комплексных чисел. | 3 ч. | [1] с.59-70 |
| ^ 5. Кольцо многочленов от одного неизвестного: определение многочлена; равенство, сумма и произведение многочленов; делимость многочленов; корни многочленов; основная теорема алгебры и следствия из неё; разложение многочлена на линейные множители; разложение многочлена с действительными коэффициентами на неприводимые множители; начальные понятия алгебры многочленов от нескольких неизвестных. | 3 ч. | [1] с.70-96, 108-111 |
| | |
| 6. Трехмерное (арифметическое) евклидово пространство 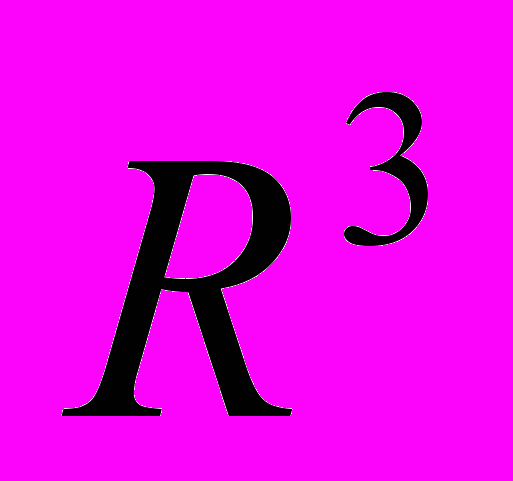 : понятие вектора (геометрическое), декартова система координат; координаты точек и векторов; базис пространства : понятие вектора (геометрическое), декартова система координат; координаты точек и векторов; базис пространства 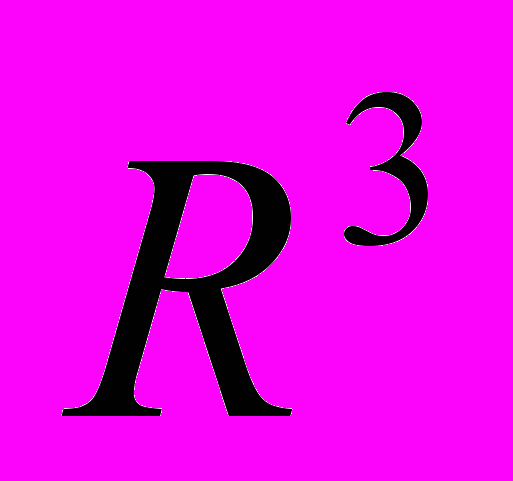 ; линейные операции над векторами; скалярное произведение и его свойства; векторное и смешанное произведения векторов, ; линейные операции над векторами; скалярное произведение и его свойства; векторное и смешанное произведения векторов, предварительные сведения из теории определителей; формулы для вычисления векторного и смешанного произведений при помощи определителей; преобразование координат вектора при изменении ориентации релера в пространстве 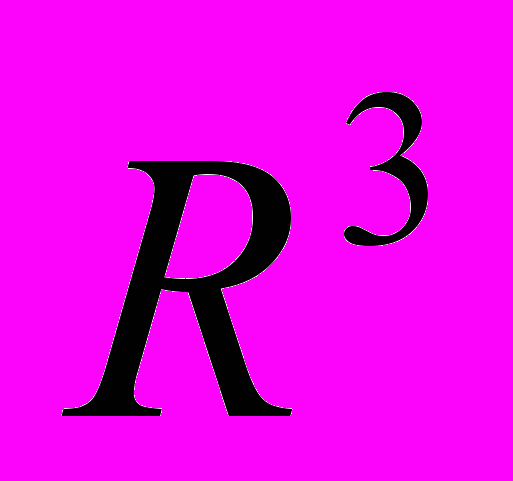 . . | 10 ч. | [1] с. 139-164, 172-184 |
| ^ 7.Прямая линия и плоскость в евклидовых пространствах  и и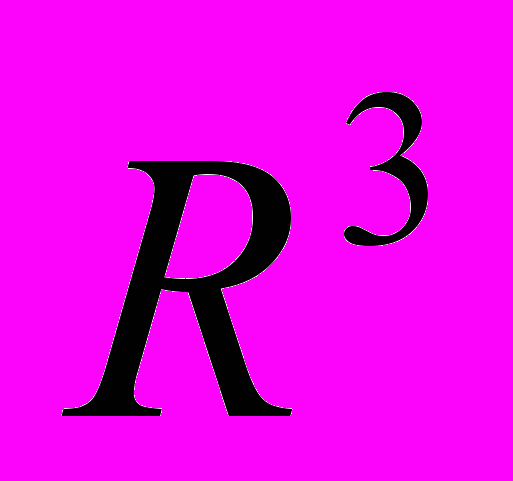 : уравнения прямой линии в пространствах : уравнения прямой линии в пространствах  и и 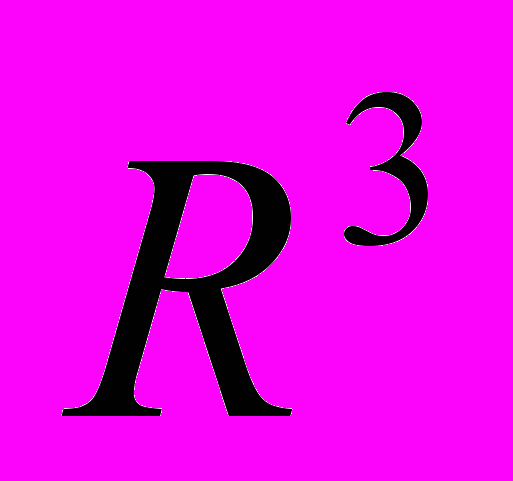 ; уравнения плоскости в пространстве ; уравнения плоскости в пространстве 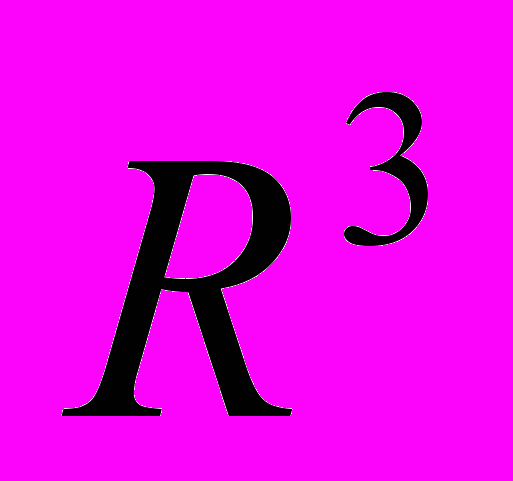 ; взаимное расположение прямой линии и плоскости в пространстве ; взаимное расположение прямой линии и плоскости в пространстве 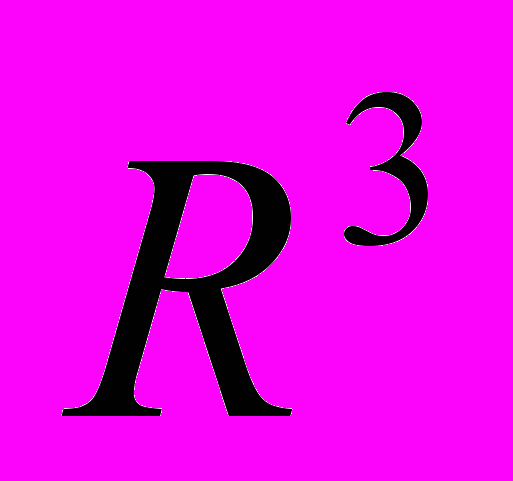 . . | 4 ч. | [1] с. 185-197 |
| ^ 8. Кривые второго порядка в пространстве  : эллипс, гипербола, парабола. : эллипс, гипербола, парабола. | 2 ч. | [1] с. 575-581 |
| ^ 9. Матрицы и определители: прямоугольные матрицы и действия над ними; ассоциативность, коммутативность и дистрибутивность операций над матрицами; понятие определителя квадратной матрицы n-го порядка; свойства и вычисление определителей; теорема об умножении определителей; обратная матрица, её существование и нахождение через союзную. Транспонирование матриц и его свойства. | 5 ч. | [1] с. 323-328, 333-342 |
| ^ 10. Системы линейных алгебраических уравнений (СЛАУ): Решение крамеровской системы линейных уравнений с помощью обратной матрицы, с помощью формул Крамера и с помощью метода Гаусса. | 2 ч. | [1] с. 342-351, 162-163, 170-172, 233-236 |
| ^ 11. Конечномерные векторные пространства: аксиоматическое определение векторного пространства; понятие линейной зависимости и независимости системы векторов; базис векторного пространства; аксиома существования конечного базиса; теорема о разложении векторов по данному базису; размерность как наименьшее число векторов, порождающих пространство. | 4 ч. | [1] с. 49-50, 228-230, 218-222 |
| ^ 12. Ранг матрицы: определение ранга через базисный минор, через линейную зависимость строк и через линейную зависимость столбцов; равносильность этих определений; нахождение ранга матрицы методом Гаусса. | 2 ч. | [1] с. 359-363 |
| ^ 13. Система линейных алгебраических уравнений (СЛАУ) общего вида: условие совместности СЛАУ, условия существования единственного решения, бесконечного множества решений. Понятие фундаментальной системы решений однородной СЛАУ. Нахождение общего решения линейно зависимой СЛАУ. | 6 ч. | [1] с. 231-237, 364-367; [4] с. 48-54 |
| | |
| ^ 14. Первичные понятия: отображение, биекция, преобразование; линейное отображение (линейный оператор); линейное преобразование (аффинор) векторного пространства; теорема о существовании и единственности линейного отображения, переводящего базис в заданную систему векторов. | 2 ч. | [1] с.24-26,22-23, 312-313;[5] с.203 |
| ^ 15. Понятие изоморфизма: изоморфизм одного векторного пространства на другое ; обратимость изоморфизма; теорема об изоморфизме n-мерных векторных пространств над данным полем; автоморфизмы (невырожденные линейные преобразования) векторных пространств; равносильность различных определений изоморфизма и автоморфизма. | 2 ч. | [1] с. 265-268, 317-320 |
| ^ 16. Матрица линейного оператора: Решение задачи об отыскании координат образа вектора при заданной матрице линейного оператора или аффинора. | 2 ч. | [1] с. 320-323, 155-159 |
| ^ 17. Алгебра операторов: действия над линейными отображениями и преобразованиями; сведение этих действий к одноименным операциям над матрицами отображений. | 2 ч. | [1] с. 315-317, 329-332, 159-162 |
| ^ 18. Преобразование координат: решение задачи об отыскании координат вектора относительно нового базиса при заданной матрице перехода от старого базиса к новому. | 3 ч. | [1] с. 352-357, 179-185 |
| ^ 19. Связь между матрицами отображений в разных базисах: решение задачи об отыскании матрицы линейного отображения в новых базисах при заданной матрице этого отображения в старых базисах. Та же задача для случая линейного преобразования. | 2 ч. | [1] с. 357-358, [5] с.215-217 [4] с. 114-115 |
| | |
| 20. Два равносильных определения подпространства. Размерность подпространства n-мерного векторного пространства. Примеры подпространств. | 1 ч. | [1] с. 254-257 |
| ^ 21. Сумма и пересечение двух подпространств: теорема о размерностях суммы и пересечения. Случай нескольких подпространств. | 2 ч. | [1] с. 257-261 |
| 22. Прямая сумма подпространств. Несколько равносильных определений прямой суммы подпространств. | 2 ч. | [1] с. 262-265 |
| ^ 23. Ядро и область значений линейного отображения; их связь со СЛАУ. Базисы этих подпространств; ранг и дефект; связь между рангом и дефектом линейного оператора. | 2 ч. | [1] с. 313-314, 317-318 |
| ^ 24. Операторы проектирования на подпространство: определение, строение матрицы; свойство идемпотентности. | 2 ч. | [1] с. 450-453 |
2 семестр (75 ч.)
| ^ НАИМЕНОВАНИЕ РАЗДЕЛА И ТЕМЫ | Обязат. ауд. занятий ч. | ЛИТЕРАТУРА (страницы) |
| ЛЕКЦИИ | | |
| | |
| 25. Собственные векторы и собственные значения линейного преобразования: определение, свойства , нахождение по заданной матрице преобразования; характеристический многочлен; свойства характеристического многочлена. | 4 ч. | [1] с. 387-394 [11] с. 20-21 |
| ^ 26. Спектр линейного преобразования: спектры алгебраический и геометрический; операторы простой структуры; операторы с простым спектром. | 4 ч. | [1] с. 394-398 [3] с. 79-82 |
| ^ 27. Инвариантные подпространства линейного преобразования: определение, примеры таких подпространств(ядро и область значений; циклические; корневые; порождённые собственными векторами). Условие инвариантности подпространства в матричной форме. Разложимость векторного пространства в прямую сумму инвариантных (для данного оператора) подпространств. Треугольная форма матрицы линейного преобразования | 6 ч. | [1] с. 398-409 с. 445-450, [3] c. 75-77 |
| ^ 28. Жорданова нормальная форма матрицы линейного преобразования: жорданова матрица и «клетки Жордана»; жорданов базис, условие существования жорданова базиса и жордановой формы для заданного линейного преобразования. | 4 ч. | [1] с. 455-462 , 479-482 |
| ^ VI. Евклидовы n-мерные векторные пространства (18 ч.) | | |
| 29. Скалярное произведение в n-мерном векторном пространстве: аксиоматическое определение; «геометрические» свойства векторов (длина, метрика, угол между векторами, ортогональность, прямоугольная проекция вектора на вектор). | 2 ч. | [1] с.200-202, 204-207,237-240 250-254,150-154 |
| ^ 30. Базисы в евклидовом пространстве: существование ортогональных и ортонормированных базисов; процесс ортогонализации Шмидта; нахождение скалярного произведения в ортонормированном базисе; ортогональные матрицы; преобразование координат вектора в ортонормированных базисах. | 4 ч. | [1] с.204-206, 240-244,247-250 152-153,427-429 |
| ^ 31. Матрица Грама системы векторов: понятие определителя Грама и матрицы Грама; критерий Грама линейной зависимости системы векторов; аффинные и евклидовы координаты вектора в данном базисе; выражение евклидовых координат через аффинные с помощью матрицы Грама. | 2 ч. | [1] с.519-521, 245-247 |
| ^ 32. Унитарные векторные пространства: скалярное произведение и ортонормированный базис; линейные функционалы и сопряженное пространство; сопряженный оператор; операторы самосопряженные и унитарные. | 5 ч. | [1] с.271-273, 409-424,434-438 |
| ^ 33. Линейные операторы в евклидовом пространстве: ортогональные преобразования и их свойства; симметрические преобразования и их свойства; оператор ортогонального проектирования на подпространство. | 5 ч. | [1] с.425-433, [4] с. 150-156; [1] с. 453-454 |
| | |
| 34. Точечно-векторные пространства: аффинные пространства (аксиоматическое определение, свойства точек и векторов, координаты их относительно репера); евклидово точечно-векторное пространство (расстояние между точками, ортонормированный репер). | 2 ч. | [1] с.214-227, 239, 508-510 |
| ^ 35. Плоскость и прямая в аффинном пространстве; инвариантное определение плоскости; процедура построения m – мерной плоскости в n – мерном пространстве; параметрические и неявные уравнения m – мерной плоскости; прямые и гиперплоскости в n – мерном пространстве. | 2 ч. | [1] с. 492-499 |
| ^ 36. Прямоугольная проекция точки и вектора на плоскость в евклидовом пространстве; перпендикуляр из точки на плоскость. Объем «параллелепипеда» в n – мерном евклидовом пространстве. Нахождение проекции и объема с помощью матрицы Грама. | 4 ч. | [1] с. 521-532 |
| ^ 37. Билинейные и квадратичные формы: определение билинейных и квадратичных форм; матрицы билинейных и квадратичных форм; симметричные билинейные формы; приведение квадратичной формы к каноническому виду; закон инерции, знакоопределенные квадратичные формы; канонический базис билинейной формы; метод Якоби; билинейные и квадратичные формы в вещественном пространстве; билинейные и квадратичные формы в евклидовом пространстве; экстремальные свойства квадратичной формы; билинейные и квадратичные формы в унитарном пространстве. | 7 ч. | [1] с. 532-569 |
| 38. Гиперповерхности в евклидовом пространстве 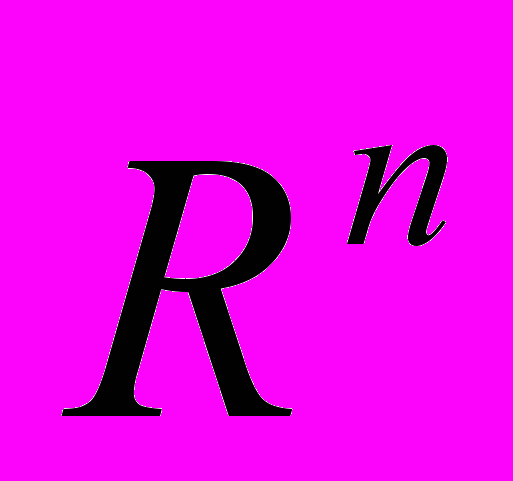 : общее уравнение гиперповерхности второго порядка в пространстве : общее уравнение гиперповерхности второго порядка в пространстве 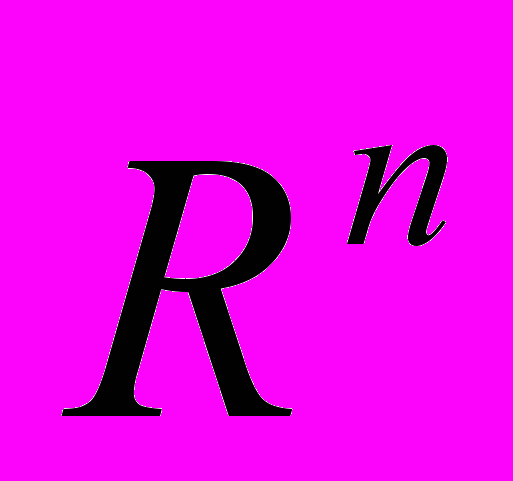 и его приведение к каноническому виду; классификация гиперповерхностей в пространстве и его приведение к каноническому виду; классификация гиперповерхностей в пространстве 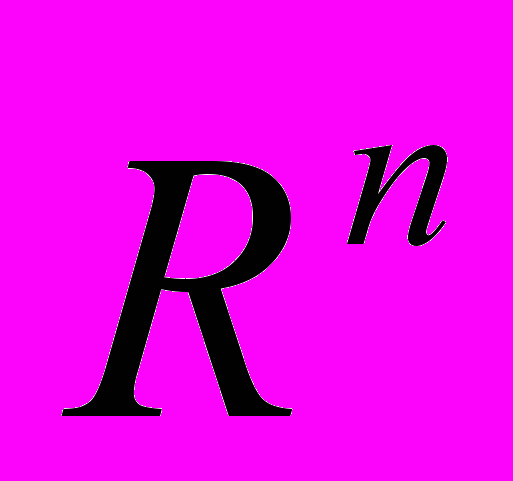 ; поверхности второго порядка в пространстве ; поверхности второго порядка в пространстве 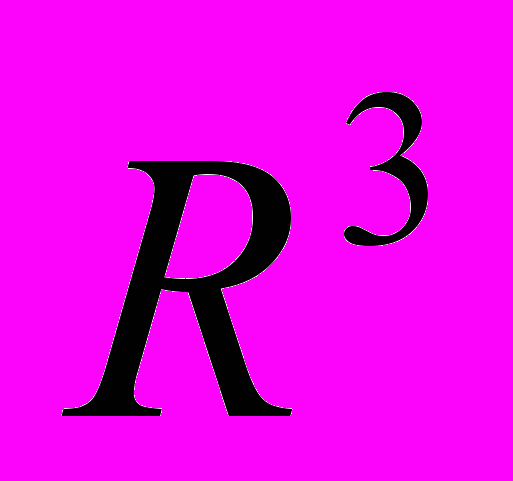 и их свойства (эллипсоид, однополостный гиперболоид, двуполостный гиперболоид, эллиптический конус, эллиптический параболоид, гиперболический параболоид, цилиндры). и их свойства (эллипсоид, однополостный гиперболоид, двуполостный гиперболоид, эллиптический конус, эллиптический параболоид, гиперболический параболоид, цилиндры). | 4 ч. | [1] с. 570-575, 582-588 |
| | |
| 39. Основная задача тензорного исчисления и общее понятие тензора: тензор как геометрический или физический объект, инвариантный относительно изменения ориентации релера; валентность геометрических и физических объектов; правило суммирования. | 2 ч. | [1] с. 588-594 |
| ^ 40. Определение тензора в аффинном пространстве: k-валентный ковариантный тензор, примеры; l - валентный контравариантный тензор, примеры; k + l – валентный (k раз ковариантный и 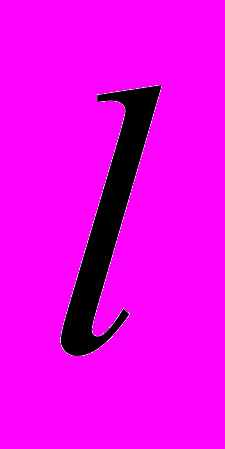 раз контравариантный ) тензор, примеры. раз контравариантный ) тензор, примеры. | 4 ч. | [1] с. 595-602 |
| ^ 41. Тензорная алгебра в аффинном пространстве: операции сложения, умножения и свертывания тензоров; операции подстановки индексов, симметрирования и альтернирования. | 5 ч. | [1] с. 602-612 |
| ^ 42. Тензорная алгебра в евклидовом пространстве: метрический тензор, операции поднятия и опускания индексов у тензора; взаимный базис и контравариантные векторы взаимного базиса. | 5 ч. | [1] с. 613-624 |
| 43. Тензорная алгебра в безиндексных (прямых) обозначениях. | 2 ч. | [1] с. 624-630 |
- ^ ТЕМАТИКА ПРАКТИЧЕСКИХ И ЛАБОРАТОРНЫХ РАБОТ
- Практические занятия
- Практические занятия
1 семестр (54 часа)
| ^ НАИМЕНОВАНИЕ РАЗДЕЛА И ТЕМЫ | Обязат. ауд. занятий ч. | ЛИТЕРАТУРА (страницы) |
| ^ ПРАКТИЧЕСКИЕ ЗАНЯТИЯ | | |
| I. Введение в общую алгебру (6 часов) | | |
| 1. Действия над комплексными числами. | 4 ч. | [1] с. 117-120, № 1.8.17-1.8.27 |
| 2. Многочлены, их корни, действия над многочленами. | 2 ч. | [1] с.120 -125, № 1.8.30-1.8.35 |
| ^ II. Линейные (векторные) пространства (34 часа) | | |
| Евклидовы пространства  и и 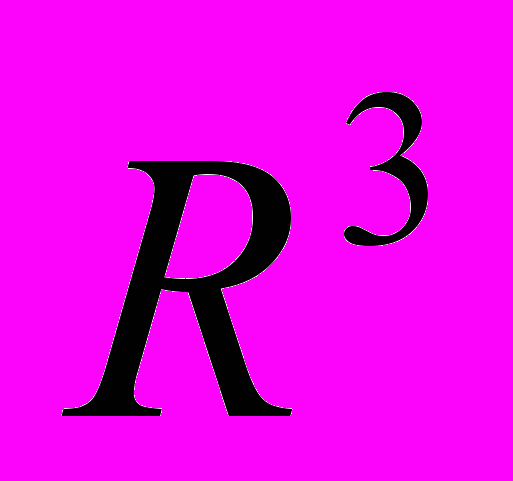 (занятия 3-11) (занятия 3-11)3. Линейные операции и коллинеарность Способы задания векторов. | 2 ч. | [1] с. 274-276, № 2.9.2-2.9.6; [13] № 759,778, 780 |
| 4. Скалярное произведение; ортогональность. | 2 ч. | [1] с. 276-281, № 2.9.7-2.9.11; [13] № 816,817, 823 |
| 5. Векторное произведение. | 2 ч. | [1] с.286 №2.9.20; [13] № 839,850, 853,860 |
| 6,7. Смешанное произведение. Компланарность и базисы. | 4 ч. | [1]с. 277, № 2.9.9; [13] № 867,870, 875,877 |
| 8. Прямая на плоскости. | 2 ч. | [1] с.274, № 2.9.4; [13] № 225,234, 269,271,275 |
| 9,10. Прямая и плоскость в пространстве 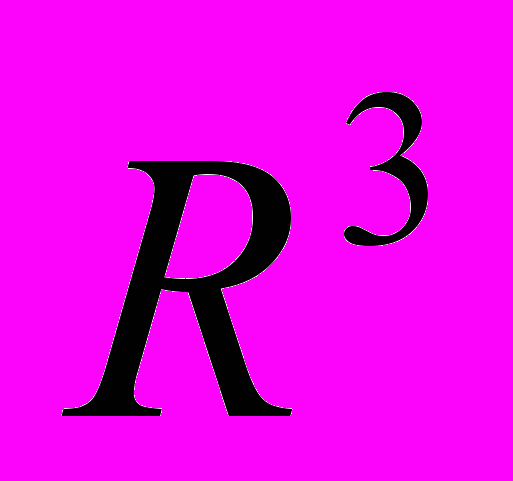 . . | 4 ч. | [1] с. 287-290, № 2.9.21-2.9.25; [13] № 1062,1072, 1079 |
| 11. Кривые 2-порядка в пространстве  . . | 2 ч. | [13] № 444,465, 515,532 |
| 12. Действия над матрицами. Обратная матрица. | 2 ч. | [1] с. 370-371, № 3.8.6, 3.8.7 с. 283 № 2.9.16 |
| 13. Решение крамеровской СЛАУ матричным методом и методом Гаусса. | 2 ч. | [1] с. 306, № [75]1; с.308-309,№ [93]4 |
| 14. Вычисление определителей методом Гаусса и по теореме Лапласа. | 2 ч. | [13] с. 197, № 1255,1256 |
| 15. Нахождение обратной матрицы с помощью метода Гаусса. | 2 ч. | [1] с. 383, № [19]1.2. |
| 16. Нахождение ранга матрицы с помощью базисного минора и с помощью метода Гаусса. | 2 ч. | [1] с.375-376, № 3.8.13, 3.8.14 |
| 17. Исследование и решение СЛАУ общего вида. | 2 ч. | [1] с. 377, № 3.8.15; с.385, № [28]2 |
| 18. Исследование и решение СЛАУ общего вида методом Гаусса. | 2 ч. | [1] с.367, № 3.7.2 |
| 19. Нахождение общего решения неоднородной СЛАУ с помощью функциональной системы решений однородной СЛАУ. | 2 ч. | [1] с.367, № 3.7.2, 3.8.15, [28] 2 |
| III. Линейные отображения и линейные преобразования n-мерного векторного пространства (8 часов) | | |
| 20. Матрица линейного оператора. Нахождение координат образа вектора при заданной матрице линейного оператора. Действия над операторами. | 2 ч. | [1] с.281,282, № 2.9.12,2.9.13; с.369, № 3.8.5 |
| 21. Преобразование координат вектора при переходе к новому базису. Проверка линейной независимости векторов «нового базиса». | 2 ч. | [1]с.384, № [25]1; с. 293,294, № 2.9.30 |
| 22,23. Нахождение матрицы линейного отображения относительно новых базисов. То же для аффинора. | 4 ч. | [1]с.373, №3.8.11; с.385, № [25]2; [14], с.43, № 183 |
| ^ IV. Линейные подпространства (6 часов) | | |
| 24. Нахождение базиса подпространства, базиса суммы подпространств. Лежит ли заданный вектор в заданном подпространстве? | 2 ч. | [1] с. 254-257 |
| 25. Ядро и область значений линейного отображения; ранг и дефект. | 2 ч. | [1] с.374-375, № 3.8.12; с. 376,377, № 3.8.14 |
| 26. Оператор проектирования. | 2 ч. | [1] с. 476-479, № 4.5.9 |
2 семестр (44 часа)
| ^ НАИМЕНОВАНИЕ РАЗДЕЛА И ТЕМЫ | Обязат. ауд. занятий ч. | ЛИТЕРАТУРА (страницы) |
| ^ ПРАКТИЧЕСКИЕ ЗАНЯТИЯ | | |
| V. Структура линейного преобразования (16 часов) | | |
| 27,28. Нахождение собственных значений и собственных векторов линейного оператора. | 4 ч. | [1] с. 482-483, № 1-4; с. 463, № 4.5.1; [14] с. 46, № 190к |
| 29,30. Спектр линейного оператора. Операторы простой структуры. | 4 ч. | [14] с. 46, № 191 а, б, в |
| 31,32. Инвариантные подпространства линейного преобразования. | 4 ч. | [1] с. 483, 484, № [6,7], [11]; [14] с. 47, № 199 а, г |
| 33,34. Нахождение жорданова базиса и жордановой нормальной формы матрицы линейного оператора. | 4 ч. | [1] с. 479-482, № 4, 5, 10 |
| ^ VI. Евклидовы n-мерные векторные пространства (8 часов) | | |
| 35. Ортогональные базисы в евклидовом пространстве. Процесс ортогонализации Шмидта. | 2 ч. | [1] с. 634-636, № 5. 7.3; [14] с. 51, № 203 а, в |
| 36. Сопряженные операторы в евклидовом и унитарном пространстве. | 2 ч. | [1] с. 467, 468, № 4. 5.4; c. 487, 488 № [23] |
| 37. Ортогональные и симметрические операторы в евклидовом пространстве. | 2 ч. | [1] с. 474-476, № 4.5.7; с.468-470 № 4.5.5 |
| 38. Построение в пространстве 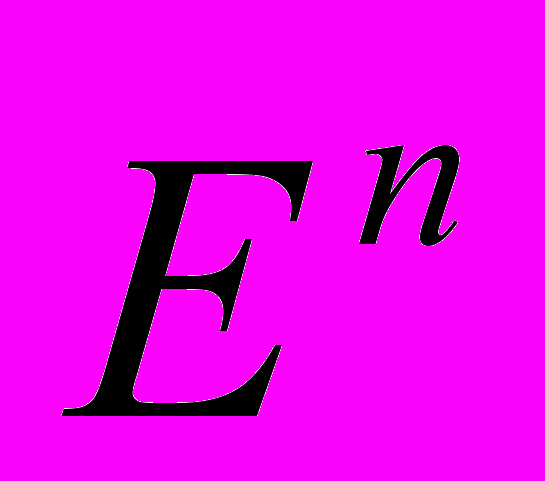 ортонормированного базиса, состоящего из собственных векторов заданного симметрического оператора. ортонормированного базиса, состоящего из собственных векторов заданного симметрического оператора. | 2 ч. | [1] с. 470-473, № 4.5.6 |
| VII. Геометрия многомерных пространств (12 часов) | | |
| 39. Плоскость и прямая в аффинном пространстве. | 2 ч. | [1] с. 631-633, № 5.7.1; c. 467 № [1], 2 |
| 40. Прямоугольная проекция точки на плоскость в евклидовом пространстве. Расстояние от точки до плоскости. | 2 ч. | [1] с. 637-639, № 5.7.4; с. 650, № [17] |
| 41. Билинейные и квадратичные формы. | 2 ч. | [1] с. 639-642, № 5.7.5-5.7.8 |
| 42. Приведение квадратичных форм к каноническому виду методом ассоциированного оператора. | 2 ч. | [1] с. С. 61, № 234 а, б |
| 43,44. Исследование поверхностей 2-го порядка по их общему уравнению. | 4 ч. | [14] с. 642-645, № 5.7.9; с. 652, 653, № [30]1 |
| VIII. Основы тензорной алгебры (8 часов) | | |
| 45,46. Преобразование координат тензора при переходе к новому базису. | 4 ч. | [1] с. 645-647, № 5.7.10; с. 654, № [37] |
| 47,48. Операции над тензорами. | 4 ч. | [1] с. 654, № [38] 1,2 |
- Контрольные работы и расчетно-графические задания
В течение каждого из двух семестров студент выполняет две контрольные работы и одно расчетно-графическое задание, включающих в себя набор задач по изучаемому курсу. Тема расчетно-графического задания выдается кафедрой математики. По результатам выполненных контрольных работ и заданий студент аттестуется или не аттестуется в семестре. Студент, не выполнивший контрольные работы или расчетно-графическое задание, не допускается к экзамену кафедрой математики.
^ 5. УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
5.1. Рекомендуемая литература
5.1.1. Основная литература
1. Сурнев В. Б. Алгебра и аналитическая геометрия. Учебное пособие. Изд-во
УГГУ, 2003. 656 с.
^ 5.1.2 . Дополнительная литература
2. Александров П. С. Введение в теорию множеств и общую топологию. М.: Наука, 1977. 368 с.
3. Кострикин А. И. Введение в алгебру. Линейная алгебра. М.: Физматлит, 2001. 368 с.
4. Головина Л. И. Линейная алгебра и некоторые ее приложения. М.: Наука, 1985. 392 с.
5. Воеводин В. В. Линейная алгебра. М.: Наука, 1980. 400 с.
6. Шилов Г. Е. Математический анализ. Конечномерные линейные пространства. М.: Наука, 1969. 432 с.
7. Гантмахер Ф. Р. Теория матриц. М.: Наука, 1988. 552 с.
8. Любарский Г. Я. Теория групп и ее применение в физике. М.: ГИТТЛ, 1957. 354 с.
9. Погорелов А. В. Геометрия. М.: Наука, 1983. 288 с.
10. Рашевский П. К. Риманова геометрия и тензорный анализ. М.: Наука, 1967. 664 с.
11. Фаддеев Д. К., Фаддеева В. Н. Вычислительные методы линейной алгебры. Изд-во 3, СП; «Лань», 2002. 733 с.
12. Эллиот Дж., Добер П. Симметрия в физике. М.: Мир, 1983. Т. 1. 368 с.
13. Клетеник Д. В. Сборник задач по аналитической геометрии. М.: Наука, 1986. 223 с.
14. Овсянников А. Я. Сборник задач по линейной алгебре. Екатеринбург, ГУ, 2001. 193 с.
5.2. Средства обеспечения освоения дисциплины
Учебно-методический комплекс, содержащий учебное пособие, в состав которого включены:
- теоретический материал,
- примеры решения типовых задач,
- задачи для самостоятельного решения.
- МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Компьютерный класс кафедры
