Рабочая учебная программа по дисциплине «Теоретические основы школьного курса математики» для ооп по направлению «050100 Педагогическое образование», магистерская программа «Математическое образование» по циклу М2 профессиональный цикл вариативная часть

Вид материала

Рабочая учебная программа

Содержание Очная форма обучения Заочная форма обучения Пояснительная записка Цели и задачи дисциплины 1.2. Место дисциплины в структуре ПрОП 1.3. Требования к результатам освоения дисциплины Уровни сформированности компетенции Повышенный уровень Уровни сформированности компетенции Повышенный уровень 1.4. Объем дисциплины и виды учебной работы Учебно-тематическое планирование 2.2. Учебно-тематический план заочной формы обучения Содержание дисциплины Перечень тем лекционных занятий Занятие № 12. Комбинаторика бинарных операций на конечных множествах Занятие № 24. Функции в школьном курсе математики. Занятие № 30. Аксиоматическое определение линейной функции. Свойства. Существование и единственность. Занятие № 32. Аксиоматическое определение показательной функции. Свойства. Существование и единственность. Занятие № 12. Функции в школьном курсе математики. ... Полное содержание

Подобный материал:

• Рабочая учебная программа по дисциплине «Алгебра» для ооп по направлению «050100 Педагогическое, 518.43kb.
• Рабочая учебная программа по дисциплине «Геометрия» для ооп направления «050100., 641.03kb.
• Рабочая учебная программа по дисциплине «Элементарная математика» для ооп «050100., 928.97kb.
• Рабочая учебная программа по дисциплине «Практикум по решению задач по математике», 239kb.
• Рабочая учебная программа по дисциплине «Конструктивная геометрия» для ооп «050100., 180.96kb.
• Рабочая учебная программа по дисциплине «Культурологические аспекты геометрии» для, 137.64kb.
• Рабочая учебная программа по дисциплине «Элементы теории графов» для ооп «050100., 334.53kb.
• Рабочая учебная программа по дисциплине «Теоретические основы школьного курса математики, 492.61kb.
• Рабочая учебная программа по дисциплине «Выпуклые тела и многогранники» для ооп «050100., 253.14kb.
• Рабочая учебная программа по дисциплине «Методика обобщающего повторения» для Проп, 154.14kb.

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Уральский государственный педагогический университет»
Математический факультет

Кафедра алгебры и теории чисел


РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА

по дисциплине «Теоретические основы школьного курса математики»

для ООП по направлению «050100 – Педагогическое образование»,

магистерская программа «Математическое образование»

по циклу М2 – профессиональный цикл

вариативная часть

Очная форма обучения Курс – 5,6 Семестр – 10,11 Объём в часах всего – 360 в т. ч.: лекции – 10 практические занятия – 110 самостоятельная работа – 240 Экзамен – 11 семестр

Заочная форма обучения Курс – 5,6 Семестр – 10, 11 Объём в часах всего – 360 в т. ч.: лекции – 12 практические занятия – 68 самостоятельная работа – 280 Экзамен – 12 семестр

Екатеринбург 2011

Рабочая учебная программа по дисциплине «Теоретические основы школьного курса математики» ГОУ ВПО «Уральский государственный педагогический университет» Екатеринбург, 2011. – 17 с.

Составитель:

Ершова Т.И., доцент кафедры алгебры и теории чисел, к.ф.-м.н., доцент, математический факультет УрГПУ


Рабочая учебная программа обсуждена на заседании кафедры алгебры и теории чисел УрГПУ (Протокол № 9 от 05.05.2011).


Зав. кафедрой С.С. Коробков


Согласовано с методической комиссией математического факультета


Председатель методической комиссии И.Н. Семенова


Декан математического факультета В.П. Толстопятов

1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
   

Несмотря на то, что содержание школьных курсов алгебры и геометрии в достаточной степени оторвано от содержания современной математической науки, учитель математики должен уметь связывать знания, полученные при изучении различных математических теорий в ВУЗе, с конкретными разделами школьного курса математики. Он должен уметь обосновывать методы, изучаемые в школе, с точки зрения высшей математики, уметь подобрать темы исследовательского характера, которые могут быть предложены учащимся в рамках исследовательских проектов. Изучение дисциплины «ТОШКМ» может помочь будущему магистру образования, специализируемущеся по профилю «Математика», увидеть школьный курс математики с такой точки зрения, которая позволяет включить его в систему общих математических и логических идей. Важно показать студентам ранее неизученные связи между понятиями и ситуациями, расширив и углубив тем самым их кругозор в направлении изучения основ алгебро-геометрического аппарата, владение которым необходимо для четких представлений об основных алгебраических понятиях, об определениях различных геометрий по «схеме Клейна», уяснения их связей с геометрическими образами. Курс призван привить магистрантам мыслительные навыки, развивающие логическое и алгоритмическое мышление, способствующее решению конструктивных и педагогико-психологических задач, направленных не только на обладание заданным объемом материала, но и на синтез межпредметных идей.

1. Цели и задачи дисциплины
   

Цели изучения дисциплины:

• Провести анализ основных разделов школьной математики с точки зрения таких фундаментальных математических понятий, как множество, отображения, изоморфизм, отношение, алгебраическая операция, число, фигура, метрика.
  
• Провести анализ логических основ школьной математики.
  
• Помочь студентам в понимании и объяснении связей между школьной и высшей математикой.
  
• Воспитать у студентов устойчивую потребность в самообразовании.
  

Задачи изучения дисциплины:

• Познакомить студентов с построением математических теорий на основе аксиоматического метода, показав его действия при использовании различных аксиоматик.
  
• Рассмотреть понятия бинарного отношения, отображения, функции с точки зрения теоретико –множественного подхода.
  
• Познакомить студентов с различными вариантами построения теории действительных чисел.
  
• Показать преимущества метрического подхода с точки зрения математического анализа и алгебры, а так же изящество и относительную «легкость» построения начальной части школьного курса геометрии на основе этого подхода.
  
• Подчеркнуть различия в построении теорий измерения линейных и угловых величин в различных аксиоматиках, площадей на классах многоугольных и квадрируемых плоских фигур, объемов на классах многогранных и кубируемых фигур.
  

1.2. Место дисциплины в структуре ПрОП

Дисциплина «Теоретические основы школьного курса математики» изучается в 10 – 11 семестрах. Ее изучение существенным образом базируется на знании школьной математики, а так же на знаниях, полученных при изучении различных дисциплин высшей математики в рамках бакалавриата. Так, основные сведения об алгебраических операциях, алгебраических системах, изоморфизмах студенты получают в курсе «Алгебра», представление об аксиоматическом построении действительных чисел – из курса «Числовые системы», о метрическом пространстве из курса «Математический анализ», о различных геометрических величинах – из курса «Геометрия».

Дисциплина «Теоретические основы школьного курса математики» призвана связать и обобщить знания, полученные при изучении разных областей математики, и на их основе сформировать взгляд на школьную математику с точки зрения отраженных в ней фундаментальных математических идей.

1.3. Требования к результатам освоения дисциплины


Процесс изучения дисциплины направлен на формирование профессиональной компетенции:

способен демонстрировать, применять, критически оценивать и пополнять математические знания,

а также части профессиональной компетенции:

готов организовывать различные виды учебно-исследовательской и проектной деятельности обучающихся.

Основные требования к результатам освоения дисциплины представлены в таблицах № 1 и № 2 в виде признаков сформированности компетенций. Требования формулируются по двум уровням: пороговый и повышенный и в соответствии со структурой, принятой в ФГОС ВПО: знать, уметь, владеть.

Таблица № 1

Уровни сформированности компетенции	Структура компетенции	Основные признаки уровня
Пороговый уровень (как обязательный для всех студентов-выпуск­ников вуза по завершению освоения дисциплины)	Знает основные положения дисциплины: «Теоретические основы школьного курса математики».	Понимает структуру построения аксиоматической теории.
		Приводит примеры аксиоматики теории множеств, действительных чисел, евклидовой планиметрии.
		Имеет представление о различных подходах к построению теории действительных чисел.
		Формулирует определения и основные свойства бинарных отношений. Приводит соответствующие примеры. (в том числе на базе школьной математики)
		Формулирует определения движений плоскости: осевой симметрии, поворота и т.д.
		Осознает сходство и различия в определениях функции, длины отрезков и «величина» угла в системах Г. Вейля, Д. Гильберта. Определяет понятие «Площадь», как функцию сначала на классе многоугольных фигур, а затем на классе квадрируемых фигур.
	Уметь доказывать утверждения дисциплины «Теоретические основы школьного курса математики». Умеет решать задачи по дисциплине «Теоретические основы школьного курса математики».	Формулирует определения функции объема сначала на классе многоугольных фигур, а затем на классе кубируемых фигур.
		Умеет аргументировано обосновывать основные положения дисциплины: «Теоретические основы школьного курса математики».
		Знает основные методы решения типовых задач из разделов: «Бинарные отношения», «Отображения», «Бинарные алгебраические операции», «Алгебраические системы».
		Знает основные методы решения типовых задач по планиметрии и стереометрии, связанные с использованием понятий расстояние между точками, от точки до прямой, от точки до плоскости, между прямыми и плоскостями.
	Владеет профессиональным языком дисциплины «Теоретические основы школьного курса математики».	Знает основные методы решения типовых задач связанные с площадями фигур и объемами фигур.
		Умеет записывать математические утверждения на языке формул логики предикатов.
		Владеет алгебраической и геометрической терминологией всех разделов дисциплины «Теоретические основы школьного курса математики».
		Способен корректно представить в математической форме сведения, полученные при изучении дисциплины «Теоретические основы школьного курса математики».
Повышенный уровень	Знает основные положения дисциплины «Теоретические основы школьного курса математики».	Устанавливает связи между основными идеями дисциплины «Теоретические основы школьного курса математики» и различными разделами элементарной математики, а так же другими математическими теориями.
		Оценивает корректность изложения математической информации в научно – популярной и методической литературе.
	Умеет доказывать утверждения дисциплины «Теоретические основы школьного курса математики».	Выделяет главные смысловые аспекты в доказательстве утверждений дисциплины «Теоретические основы школьного курса математики».
		Распознает ошибки в рассуждениях о свойствах объектов и процессов изучаемых школьном курсе математики. (А так же ТОШКМ).
		Приводит обоснование алгоритмов, методов решения задач применяющихся в школьном курсе математики.
		Понимает границы использования полноты и строгости изложения теоретического материала в школьной математике.
	Умеет решать задачи дисциплины «Теоретические основы школьного курса математики».	Оценивает различные методы решения задачи и выбирает оптимальный способ.
		Способен привести примеры бинарных отношений из школьной математики и проверить справедливость свойств этих отношений.
		Способен привести примеры отображений из школьной математики и проверить справедливость свойств этих отображений.
		Может решать геометричесикие задачи в том числе и связанные с геометрическими величинами (длинами, площядями, объемами) с помощью применения движений разных видов.
	Владеет профессиональным языком, используемым в дисциплине «Теоретические основы школьного курса математики».	Критически осмысливает полученные знания.
		Способен проявить свою компетентность в алгебре в обосновании некоторых тем и разделов школьного курса математики в том числе и с точки зрения высшей математики в различных ситуациях: В разных формах работы со школьниками, участие в работе семинаров, конференций и т.д.
		Способен грамотно передавать результат проведенных исследований в виде конкретных рекомендаций на математическом языке.

Таблица № 2

Уровни сформированности компетенции	Структура части компетенции	Основные признаки уровня
Пороговый уровень (как обязательный для всех студентов-выпуск­ников вуза по завершению освоения дисциплины)	Знает этапы исследования.	Знает, какие типы задач школьного курса математики имеют связи и получают обоснование в дисциплине «Теоретические основы школьного курса математики».
		Знает основные задачи исследовательского типа из дисциплины «Теоретические основы школьного курса математики».
	Может разработать исследовательские задания на материале школьного курса математики.	Может предложить конкретные задачи исследовательского типа из алгебры и геометрии имеющие выход в различные разделы высшей математики.
		Может составить задачу и составить план решения предложенной задачи.
	Может организовать локальную исследовательскую деятельность учащихся.	Может сформулировать цель, гипотезу, предложить пути решения задачи.
		Способен оценить полученные результаты и наметить пути дальнейшего исследования.
Повышенный уровень	Знает основные требования, предъявляемые к проектам.	Знает темы, связанные с дисциплиной «Теоретические основы школьного курса математики» и подходящие для разработки исследовательских проектов со школьниками.
	Умеет выбрать тему исследовательского проекта.	Может сформулировать цель, гипотезу, объект и предмет исследовательского проекта.
	Владеет основами организации работы над проектом.	Способен организовать исследовательскую деятельность группы участников по выбранной теме проекта.

1.4. Объем дисциплины и виды учебной работы


Согласно учебному плану курс «Теоретические основы школьного курса математики» на очном отделении изучается магистрантами на 5 курсе в 10 и на 6 курсе в 11 семестре, форма контроля – экзамен в 11 семестре. На изучение курса отводится 360 учебных часов, в т.ч. 120 уч.ч. аудиторных занятий и 240 уч.ч. самостоятельной работы студентов (СРС). Аудиторные занятия включают 10 уч.ч. лекций и 110 уч.ч. практических занятий.

Предусматривается так же выполнение четырех контрольных работ в соотвествии с графиком проведения контрольных мероприятий. Контроль и организация самостоятельной работы студентов осуществляются с помощью домашних заданий, охватывающих все наиболее важные разделы курса.

На заочном отделении дисциплина «Теоретические основы школьного курса математики» изучается на 5 курсе в 10 семестре и на 6 курсе в 11 семестре. Форма отчетности экзамен в 12 семестре. На изучение курса отводится также 360 учебных часов, в т.ч. 80 уч.ч. аудиторных занятий и 280 уч.ч. самостоятельной работы студентов (СРС). Аудиторные занятия включают 12 уч.ч. лекций и 68 уч.ч. практических занятий. Предусматривается также выполнение домашней контрольной работы с представлением решения в 12 семестре.


Общая трудоемкость дисциплины составляет четыре зачетные единицы.

2. УЧЕБНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

2.1. Учебно-тематический план очной формы обучения

№ п/п	Наименование раздела, темы	Всего тру- доем- кость	Аудиторные занятия				Самостоя- тель- ная работа
			Все- го	Лек- ции	Пра- кти- чес- кие	Ла- бора- тор- ные
1	Теория множеств как основа математики.	18	6		6		12
2	Бинарные отношения и отображения.	48	16	2	14		32
3	Алгебраические операции.	30	10		10		20
4	Действительные числа и школьная математика.	48	16	2	14		32
5	Функции в школьном курсе математики.	96	32	2	30		64
6	Метрическая аксиоматика геометрии.	48	16	2	14		32
7	Геометрия величины.	7	24	2	22		48
	Итого	360	120	10	110		240

2.2. Учебно-тематический план заочной формы обучения


10 семестр

№ п/п	Наименование раздела, темы	Всего тру- доем- кость	Аудиторные занятия				Самостоя- тель- ная работа
			Все- го	Лек- ции	Пра- кти- чес- кие	Ла- бора- тор- ные
1	Теория множеств как основа математики.	26	6	2	4		20
2	Бинарные отношения и отображения.	52	12	2	10		40
3	Алгебраические операции.	30	6		6		24
4	Функции в школьном курсе математики.	72	16	2	14		56
	Итого	180	40	6	34		140

11 семестр

№ п/п	Наименование раздела, темы	Всего тру- доем- кость	Аудиторные занятия				Самостоя- тель- ная работа
			Все- го	Лек- ции	Пра- кти- чес- кие	Ла- бора- тор- ные
1	Действительные числа и школьная математика.	38	8	2	6		30
2	Метрическая аксиоматика геометрии.	64	14	2	12		50
3	Геометрия величины.	78	18	2	16		60
	Итого	180	40	6	34		140

3. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
   
   1. Структурированное содержание дисциплины
      

№ п/п	Наименование раздела (темы)	Содержание раздела
1	Теория множеств как основа математики.	«Наивная теория множеств». Подразделы теории множеств. Аксиоматика Цермело –Френкеля. Множества в школьной математике.
2	Бинарные отношения и отображения.	Бинарные отношения. Свойства бинарных отношений, бинарные отношения с различными наборами свойств. Операции над бинарными отношениями, их связь со свойствами бинарных отношений. Отношения эквивалентности и классификация. Комбинаторика бинарных отношений на конечных множествах. Бинарные отношения в школьной математике. Отображения множеств. Частные виды отображений. Комбинаторика отображений конечных множеств. Отображения в школьном курсе математики.
3	Алгебраические операции.	Алгебраическая операция. Бинарные алгебраические операции, их свойства. Комбинаторика бинарных операций на конечных множествах. Алгебры. Упорядочение алгебрыю. Поле частных области целостности. Алгебраические операции и алгебры в школьном курсе математики.
4	Действительные числа и школьная математика.	Аксиоматика действительных чисел. Построение действительных чисел с помощью сечений Дедекинда. Действительные числа в школьном курсе математики.
5	Функции в школьном курсе математики.	Функция как частный случай отношения. Функции действительных переменных, их свойства. Аксиоматика определения элементарных функций, свойства. Теоремы существования и единственности. Линейная, степенная, показательная, логарифмическая функции, как изоморфизмы числовых групп. Определение тригонометрических функций на яхыке гомоморфизмов групп.
6	Метрическая аксиоматика геометрии.	Сигнатура и аксиоматика евклидовой планиметрии по В. Ф. Кагану, А.Н. Колмогорову, А.В. Погорелову в сравнении с системами Д. Гильберта и Г. Вейля. Понятие движения. Группа движений плоскости. Геометрические инварианты движений. Осевая симметрия, центральная симметрия, поворот. Понятие прямого угла и перпендикулярности прямых. Расстояние от точки до прямой. Пересечение прямой с окружностью и пересечения двух окружностей.
7	Геометрия величины.	Понятие измерения длин отрезков и величин углов в абсолютной геометрии. Существование и единственность функции «длина отрезка» и «величина угла» в системах Г. Вейля и Д. Гильберта. Реализация функции «длина отрезка» и «длина угла» в арифметической модели евклидовой геометрии и модели Кэли – Клейна планиметрии Лобачевского. Существование и единственность функции «площадь» на классе многоугольных фигур. Квадрируемые фигуры и нуль – фигуры. Многоугольные фигуры и их объемы. Кубируемые фигуры и их объемы.

2. Перечень тем лекционных занятий
   

На очном отделении отделении:

Лекция № 1 Бинарные отношения и отображения в школьном курсе математики

Лекция № 2. Различные подходы к построению действительных чисел.

Лекция № 3. Аксиоматический подход к определению элементарных функций

Лекция № 4. Схема построения евклидовой планиметрии на основе метрической аксиоматики.

Лекция № 5. Геометрические величины (длины, площади, объемы) как определенные аксиоматически числовые функции на классах геометрических фигур.

На заочном отделении отделении:

Лекция № 1. Аксиоматический подход к построению теории множеств.

Лекция № 2 Бинарные отношения и отображения в школьном курсе математики

Лекция № 3. Различные подходы к построению действительных чисел.

Лекция № 4. Аксиоматический подход к определению элементарных функций

Лекция № 5. Схема построения евклидовой планиметрии на основе метрической аксиоматики.

Лекция № 6. Геометрические величины (длины, площади, объемы) как определенные аксиоматически числовые функции на классах геометрических фигур.

3. Перечень тем практических занятий
   

На очном отделении:

Занятие № 1. Наивная теория множеств.

Занятие № 2. Аксиоматика Цермело –Френеля. Следствия.

Занятие № 3. Теория множеств в школьном курсе математики.

Занятие № 4. Бинарные отношения. Свойства бинарных отношений.

Занятие № 5. Операции над бинарными отношениями.

Занятие № 6. Отношения эквивалентности и отношения частичного порядка в школьном курсе математики.

Занятие № 7. Комбинаторика бинарных отношений на конечных множнствах.

Занятие № 8. Отображения. Свойства отображений. Связь с отношениями.

Занятие № 9. Отображения в школьном курсе математики.

Занятие № 10. Комбинаторика отображений конечных множеств.

Занятие № 11. Алгебраические операции. Свойства бинарных алгебраических операций.

Занятие № 12. Комбинаторика бинарных операций на конечных множествах

Занятие № 13. Алгебры. Упорядочение алгебры.

Занятие № 14. Поле частных области целостности.

Занятие № 15. Алгебраические операции и алгебры в школьном курсе математики.

Занятие № 16. Аксиоматика действительных чисел. Следствия.

Занятие № 17. Построение действительных чисел с помощью сечений Дедекинда.

Занятие № 18. Построение действительных чисел с помощью сечений Дедекинда.

Занятие № 19. Представление рациональных чисел конечными или бесконечными периодическими десятичными дробями.

Занятие № 20. Операции над десятичными дробями. Свойства операций.

Занятие № 21. Сравнение десятичных дробей по величине. Свойства отношения сравнения.

Занятие № 22. Полнота множества действительных чисел..

Занятие № 23. Функции действительной переменной. Их свойтсва.

Занятие № 24. Функции в школьном курсе математики.

Занятие № 25. Обратные функции. Условия существования обратной функции.

Занятие № 26. Графики функций. Преобразования графиков.

Занятие № 27. Графические способы решения уравнений..

Занятие № 28. Графические способы решения систем уравнений и неравенств.

Занятие № 29. Группы. Гомоморфизмы и изоморфизмы групп.

Занятие № 30. Аксиоматическое определение линейной функции. Свойства. Существование и единственность.

Занятие № 31. Аксиоматическое определение степенной функции. Свойства. Существование и единственность.

Занятие № 32. Аксиоматическое определение показательной функции. Свойства.

Существование и единственность.

Занятие № 33. Аксиоматическое определение логарифмической функции. Свойства Существование и единственность.

Занятие № 34. Аксиоматическое определение тригонометрических функций.

Занятие № 35. Свойства тригонометрических функций.

Занятие № 36. Существование и единственность тригонометрических функций.

Занятие № 37. Композиция функций.

Занятие № 38. Движения плоскости их геометрические инварианты и задачи на движение с данным количеством неподвижных точек.

Занятие № 39. Осевые симметрии.

Занятие № 40. Центральные симметрии.

Занятие № 41. Повороты как движения с единственной неподвижной точкой. (или тождественные).

Занятие № 42. Понятия прямого угла и перпендикуляра, задачи о связи между перпендикулярностью прямых и осевыми симметриями.

Занятие № 43. Задача о проведении перпендикуляра к данной прямой через данную точку. Расстояние от точки до прямой.

Занятие № 44. Пересечение прямой с окружностью и пересечение двух окружностей. Признаки конгруэнтности треугольников.

Занятие № 45. Измерение длин отрезков и величин углов в абсолютной геометрии и в аксиоматике Г. Вейля.

Занятие № 46. Функции «длина отрезка» и «величина угла» в системе Д. Гильберта.

Занятие № 47. Реализация функций «длина отрезка» и «величина угла» в арифметической модели евклидовой геометрии и в модели Кэли – Клейна планиметрии Лобачевского.

Занятие № 48. Выпуклые многоугольники и многоугольные фигуры. Нахождение площадей многоугольных фигур.

Занятие № 49. Равносильность равновеликости и равносоставленности многоугольных фигур.

Занятие № 50. Функция площадь на классе квадрируемых фигур, ее связь с характером линии, ограничивающей фигуру. Нахождение площадей.

Занятие № 51. Поведение площади фигуры при аффинных преобразованиях.

Занятие № 52. Функция объема на классе многогранных фигур.

Занятие № 53. Существование равновеликих, но не равносоставленных многогранных фигур. Теорема Дена.

Занятие № 54. Вычисление объемов пирамиды с использованием геометрических прогрессий.

Занятие № 55. Функция объема на классе многогранных фигур. Класс кубируемых фигур и функция объема на нем.


На заочном отделении:

10 семестр

Занятие № 1. Аксиоматика Цермело –Френеля. Следствия.

Занятие № 2. Теория множеств в школьном курсе математики.

Занятие № 3. Бинарные отношения. Свойства бинарных отношений.

Занятие № 4. Операции над бинарными отношениями.

Занятие № 5. Отношения эквивалентности и отношения частичного порядка в школьном курсе математики.

Занятие № 6. Отображения. Свойства отображений. Связь с отношениями.

Занятие № 7. Отображения в школьном курсе математики.

Занятие № 8. Алгебраические операции. Свойства бинарных алгебраических операций.

Занятие № 9. Алгебры. Упорядочение алгебры.

Занятие № 10. Алгебраические операции и алгебры в школьном курсе математики.

Занятие № 11. Функции действительной переменной. Их свойства.

Занятие № 12. Функции в школьном курсе математики.

Занятие № 13. Графики функций. Преобразования графиков

Занятие № 14. Графические способы решения систем уравнений и неравенств.

Занятие № 15. Аксиоматическое определение линейной функции. Свойства. Су ществование и единственность.

Занятие № 16. Аксиоматическое определение степенной функции. Свойства. Существование и единственность.

Занятие № 17. Аксиоматическое определение показательной и логарифмической функции. Свойства.

11 семестр


Занятие № 1. Аксиоматика действительных чисел. Различные модели этой аксиоматики.

Занятие № 2. Операции над десятичными дробями. Свойства операций.

Занятие № 3. Сравнение десятичных дробей по величине. Свойства отношения сравнения. Полнота множества действительных чисел.

Занятие № 4. Движения плоскости их геометрические инварианты и задачи на движение с данным количеством неподвижных точек.

Занятие № 5. Осевые и центральные симметрии.

Занятие № 6. Повороты как движения с единственной неподвижной точкой. (или тождественные).

Занятие № 7. Понятия прямого угла и перпендикуляра, задачи о связи между перпендикулярностью прямых и осевыми симметриями.

Занятие № 8. Задача о проведении перпендикуляра к данной прямой через данную точку. Расстояние от точки до прямой.

Занятие № 9. Пересечение прямой с окружностью и пересечение двух окружностей. Признаки конгруэнтности треугольников.

Занятие № 10. Измерение длин отрезков и величин углов в абсолютной геометрии и в аксиоматике Г. Вейля.

Занятие № 11. Функции «длина отрезка» и «величина угла» в системе Д. Гильберта.

Занятие № 12. Выпуклые многоугольники и многоугольные фигуры. Нахождение площадей многоугольных фигур.

Занятие № 13. Функция площади на классе квадрируемых фигур. Ее связь с характером линии, ограничивающей фигуру. Нахождение площадей.

Занятие № 14. Функция объема на классе многогранных фигур.

Занятие № 15. Существование равновеликих, но не равносоставленных многогранных фигур

Занятие № 16. Вычисление объемов пирамиды с использованием геометрических прогрессий.

Занятие № 17. Класс кубируемых фигур и функция объема нем

4. Перечень тем лабораторных работ
   

Согласно учебному плану выполнение работ по данной дисциплине не предусмотрено.

5. Вопросы для контроля и самоконтроля
   

1. Парадоксы теории множеств.
   
2. Система аксиом Цермелло – Френнеля.
   
3. Определение бинарного отношения. Примеры.
   
4. Свойства бинарных отношений.
   
5. Отношение эквивалентности. Связь с разбиениями множества.
   
6. Отношение частичного и линейного порядка. Примеры.
   
7. Бинарные отношения в школьном курсе математики.
   
8. Отображение множеств. Примеры (в частности из школьного курса математики).
   
9. Свойства отображений.
   
10. Композиция отображений.
    
11. Алгебраические операции. Примеры (в частности из школьного курса математики).
    
12. Свойства бинарных алгебраических операций.
    
13. Алгебра, Группа, Кольцо, Поле. Примеры.
    

3.6 Перечень тем занятий, реализуемых в активной и интерактивной формах


Каждая лекция содержит в себе интерактивные фазы проведения занятия. Так например, при изучении темы «Бинарные отношения и отображения» в школьном курсе математики студенты приводят примеры бинарных отношений и отображений, играющих важную роль как в различных разделах школьной математики, так и в различных разделах дисциплин высшей математики. Перечисляют свойства, которыми они обладают. При изучении темы: «Схема построения евклидовой планиметрии на основе метрической аксиоматики» приводят определения и примеры различных движений плоскости: поворота, осевой и центральной симметрии и др., известных им из курса «Геометрия».

Все практические занятия проводятся в интерактивной форме, начиная с анализа условия задач до обсуждения вариантов решения.


4. САМОСТОЯТЕЛЬНАЯ РАБОТА И ОРГАНИЗАЦИЯ

КОНТРОЛЬНО-ОЦЕНОЧНОЙ ДЕЯТЕЛЬНОСТИ


4.1. Темы, вынесенные на самостоятельное изучение для студентов заочной форм обучения

1. Парадоксы теории множеств.
   
2. Операция композиции отображений. Свойства этой операции.
   
3. Определите свойства функции
   
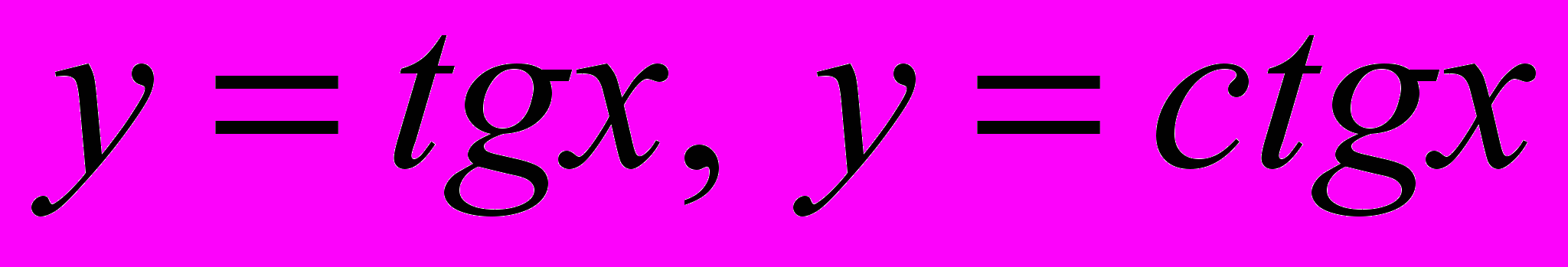
4. Определение и существование биссектрисы угла.
   
5. Теорема о равнобедренном треугольнике. Следствия о наклонных.
   
6. Измерение углов в системах Вейля и Гильберта.
   
7. Равносоставленность равновеликих параллелограммов с одинаковыми основаниями.
   

4.2. Темы для контрольных работ для студентов очной и заочной форм обучения

1. Бинарные отношения и отображения.
   
2. Алгебры. Функции.
   
3. Движения плоскости.
   
4. Нахождения площадей многоугольных и квадируемых фигур.
   

4.3. Примерные темы курсовых работ


Курсовые работы по дисциплине ТОШКМ не предусмотрены.


4. 4. Вопросы для подготовки к теоретической части зачета

1. Теория множеств в школьной математики.
   
2. Бинарные отношения в школьной математике.
   
3. Отображения в школьном курсе математики.
   
4. Алгебраические операции и алгебры в школьном курсе математики.
   
5. Построение системы действительных чисел с помощью сечений Дедекинда.
   
6. Действительные числа в школьном курсе математики.
   
7. Аксиоматические определения линейной степенной функции. Свойства. Теоремы существования и единственности.
   
8. Аксиоматические определения линейной степенной функции. Свойства. Теоремы существования и единственности.
   
9. Аксиоматические определения показательной и логарифмической функции. Свойства. Теоремы существования и единственности.
   
10. Определения тригонометрических функций на языке гомоморфизмов групп.
    
11. Сигнатура и аксиоматика евклидовой плоскости по А.Н. Колмогорову в сравнении с системами Д.Гильберта и Г. Клейна.
    
12. Понятие движения. Группа движений плоскости. Геометрические инварианты движений.
    
13. Аксиома подвижности, . Движения с двумя и тремя неподвижными точками.
    
14. Существование и единственность функции «длина отрезка» в системе Г. Вейля.
    
15. Существование и единственность функции «длина отрезка» в системе Д. Гильберта.
    
16. Измерение углов в системах Вейля и Гильберта.
    
17. Существование и единственность функции «площадь» на классе многоугольных фигур.
    
18. Теорема Бойом – Гервина о равносоставленности равновеликих многоугольных фигур.
    
19. Квадрируемые фигуры и нуль – фигуры. Критерий квадрируемрсти фигуры в терминах ее границы. Свойства линий как границ фигур.
    
20. Кубируемые фигуры и их объемы.
    

21. Скалярные величины.

4.5. Типы задач для подготовки к практической части экзамена.

1. Задачи, связанные с проверкой свойств бинарных отношений.
   
2. Задачи, связанные с проверкой свойств отображений.
   
3. Задачи, связанные с проверкой свойств бинарных операций.
   
4. Задачи, связанные с проверкой свойств функций.
   
5. Задачи, связанные с применением осевых симметрий поворотов, параллельных переносов, гомотетий (в частности, задачи на построение).
   
6. Задачи на нахождение площадей многоугольных фигур.
   
7. Задачи на нахождение площадей фигур, ограниченных линиями определенных видов.
   
8. Задачи на нахождение объемов многогранных фигур.
   
9. Задачи на нахождение объемов некоторых кубируемых фигур средствами математического анализа.
   
10. Сравните заданные математические объекты. Выделите свойства, присущие всем указанным объектам. Сформулируйте свойства, присущие только некоторым (не всем) объектам. Укажите свойства, которыми не обладает ни один из указанных объектов.
    
11. Сравните заданные различные определения одного и того же математического объекта. Проанализируйте, какие математические сведения необходимы для этих определений. Докажите равносильность этих определений.
    
12. Установите пробел в предложенном доказательстве теоремы.
    
13. Приведите примеры и контрпримеры для заданного определения.
    
14. Решите предложенную математическую задачу. Сформулируйте все необходимые для решения определения и факты.
    

5. УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОМАЦИОННОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ


5.1. Рекомендуемая литература

Основная

1. Атанасян, Л. С., Денисова И. С, Г.В. Силаев. – М.: Санта – Пресс, 1997. Курс элементарной геометрии: в 2 ч. : учеб. пособие для студ. ин-тов и для учащихся классов с углубленным изучением математики . М.: Санта – Пресс, 1997.
   
2. Болтянский, В.Г. Равносоставленность многоугольников и многогранников. Энциклопедия элементарной математики. Кн. 5. Геометрия. – М.:ГИФМЛ, 1961. – С.142-181.
   
3. Виленкин, Н.Я., Дуничев К. И., Калужнин Л. А., А.А. Столяр А.А.. Современные основы школьного курса математики. М.: Наука, 1980.– 287 с.
   
4. Виленкин, Н.Я., Литвиненко В. Н., Модкович А.Г., Элементарная математика: учеб. пособие для студентов заочников физ.-мат. фак. пед. ин-тов. Нарофоминск: Академия. 2004.–222с.
   
5. Ефимов, Н.В. Высшая геометрия. учеб. пособие для студентов матем. спец. высш.уч. заведений. М.: Физматлит, 2003. –584 с.
   
6. Клейн Ф. Элементарная математика с точки зрения высшей. : Лекции, читанные в Гёттенбергском университете: в 2 ч./ пер. с нем. Д. А. Крыжановского; под ред. В. Г. Болтянского. – 2-у изд. М.: Наука, 1987.
   
7. Любецкий В. А. Основные понятия школьной математики: учеб. пособие для студ. пед. ин-тов. М.: Просвещение, 2004. – 264 с.
   
8. Рохлин, В.А. Площадь и объем. Энциклопедия элементарной математики. Кн. 5. Геометрия. – М.:ГИФМЛ, 1966. – С.7-88.
   
9. Смирнова И. М., Смирнов В. А. Геометрия. Расстояния и углы в пространстве.: учеб. –метод. пособие/ 2-е изд., перераб.
   

Дополнительная

1. Тихомиров В. М., Прасолов В. В.Геометрия: для школьников, студентов, учителей математики Изд. 2-е, испр. М.: Изд-во МЦНМО, 2007.-328 с.
   
2. Понарин Я. П. Элементарная геометрия: (для школьников сред. Кл, учителей математики и студентов вузов) Изд. 2 –е, стер. М.: Изд-во МЦНМО.
   

6. МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ И ДИДАКТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ


Программное обеспечение

При изучении дисциплины «Теории и основы школьного курса математики» Рекомендуется использовать технические средства обучения (персональные компьютеры, медиа проектор).


7. СВЕДЕНИЯ ОБ АВТОРЕ ПРОГРАММЫ


Ершова Т.И.,

к.ф.-м.н.,

доцент,

доцент алгебры и теории чисел УрГПУ

Рабочий телефон: (343) 371-45-97


РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА

по дисциплине «Теоретические основы школьного курса математики»

для ООП по направлению «050100 – Педагогическое образование»,

магистерская программа «Математическое образование»,

по циклу М.2 – профессиональный цикл,

вариативная часть


Подписано в печать Формат 6084/16

Бумага для множительных аппаратов. Усл. печ. л. .

Тираж экз. Заказ .

Уральский государственный педагогический университет

620017 Екатеринбург, пр. Космонавтов, 26