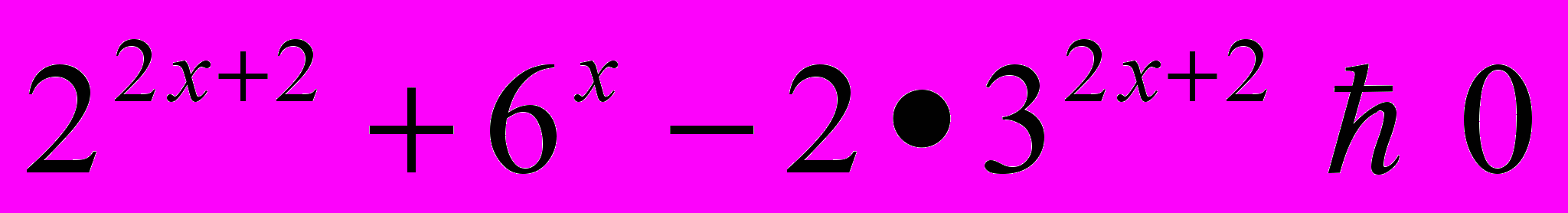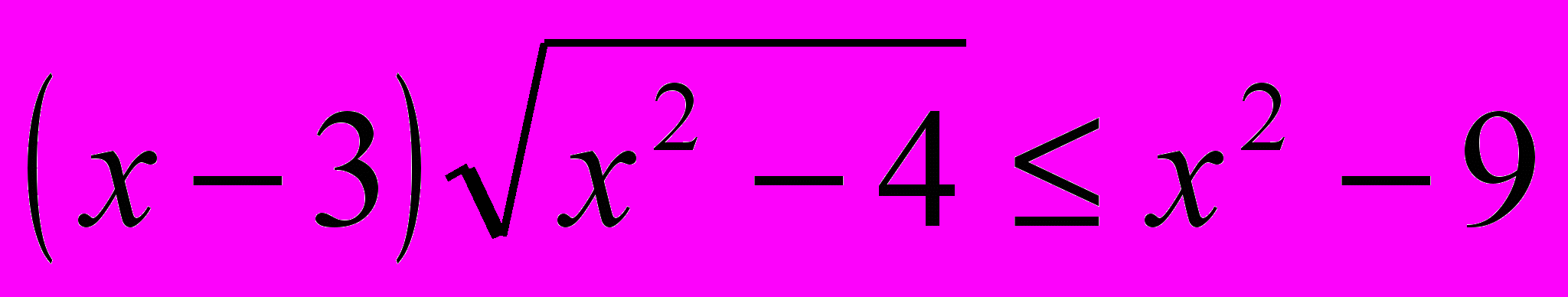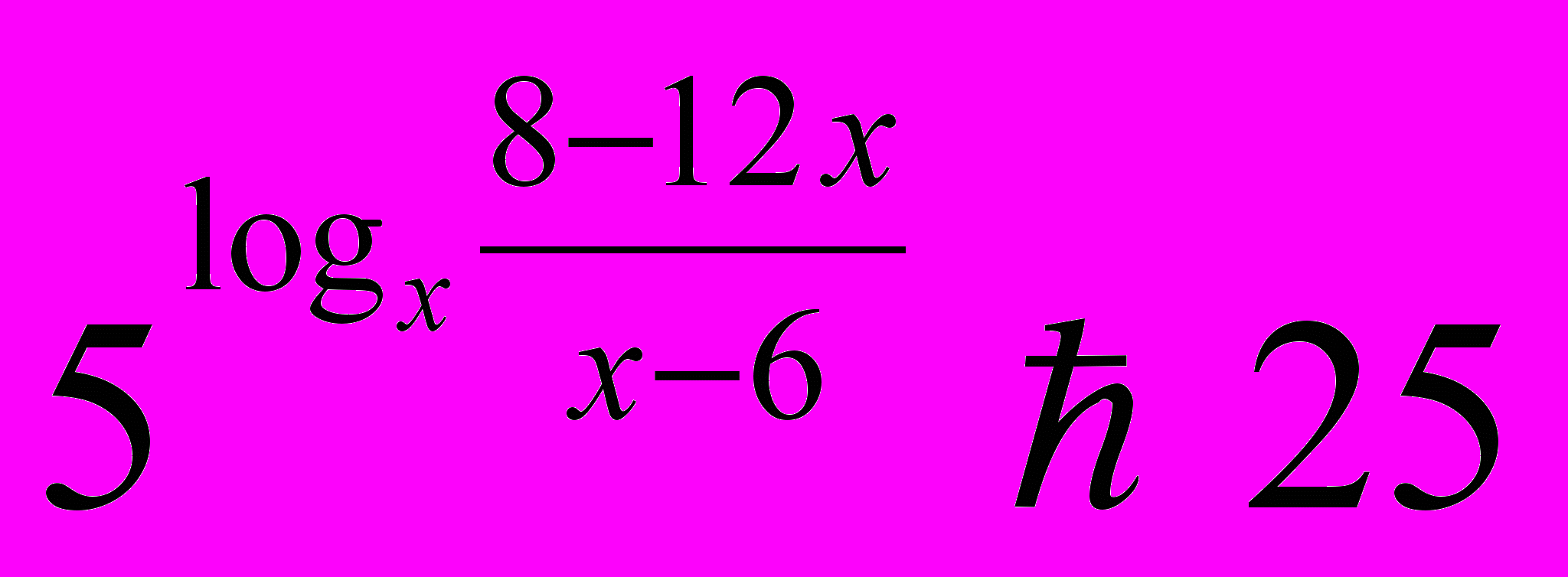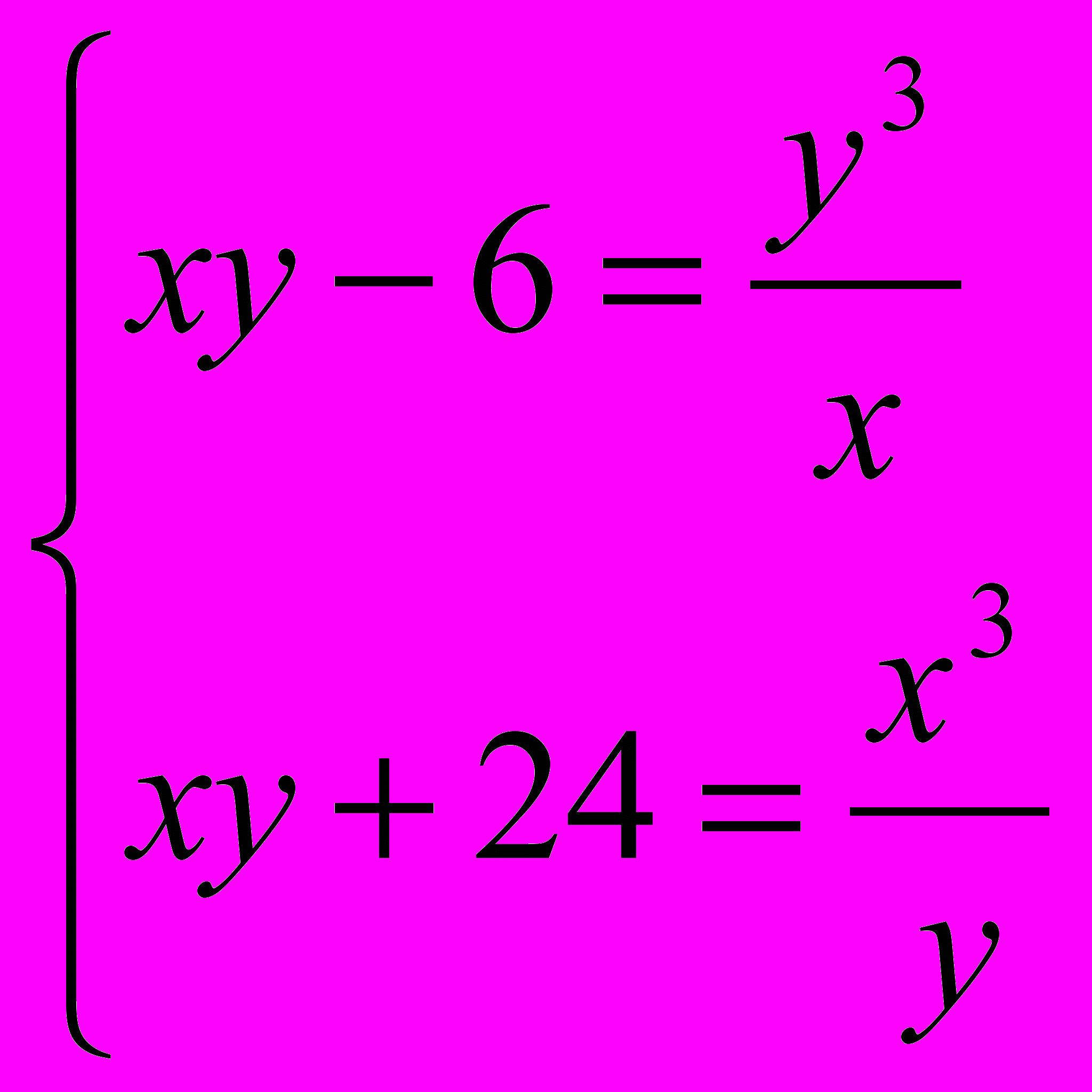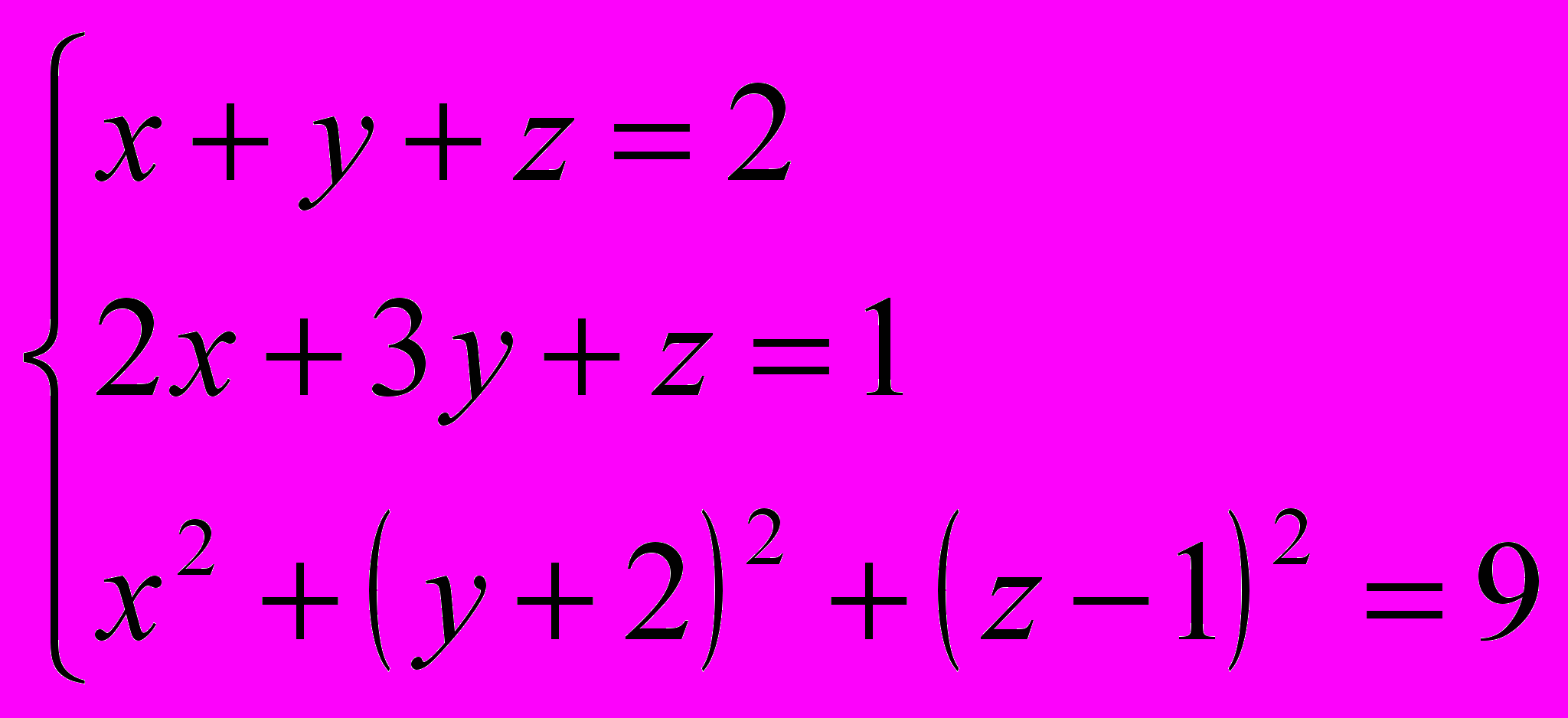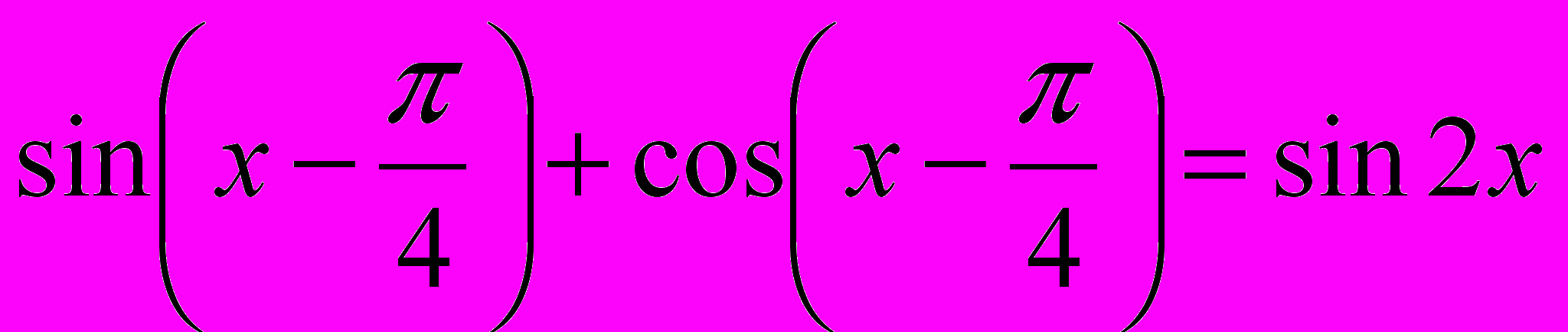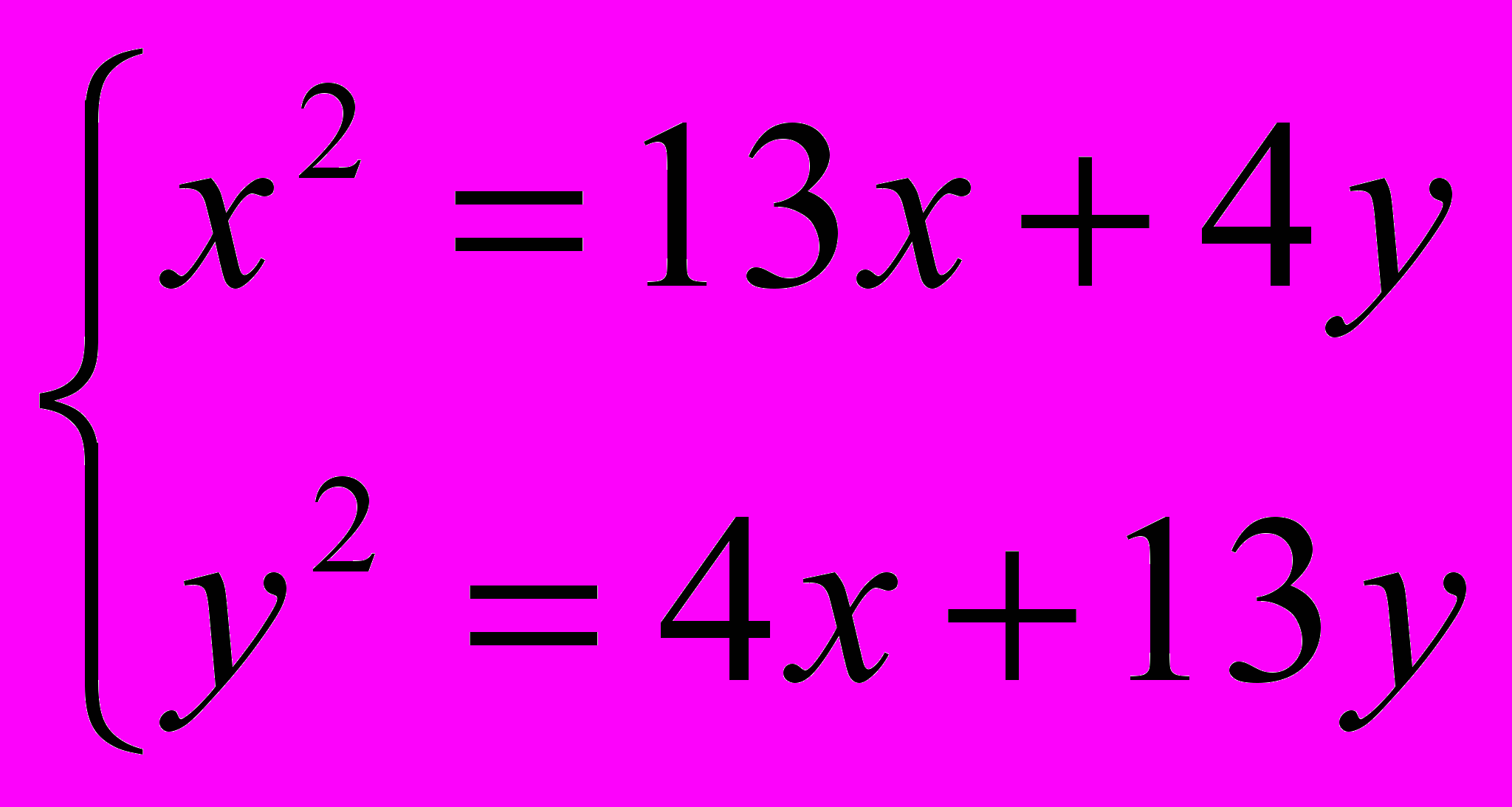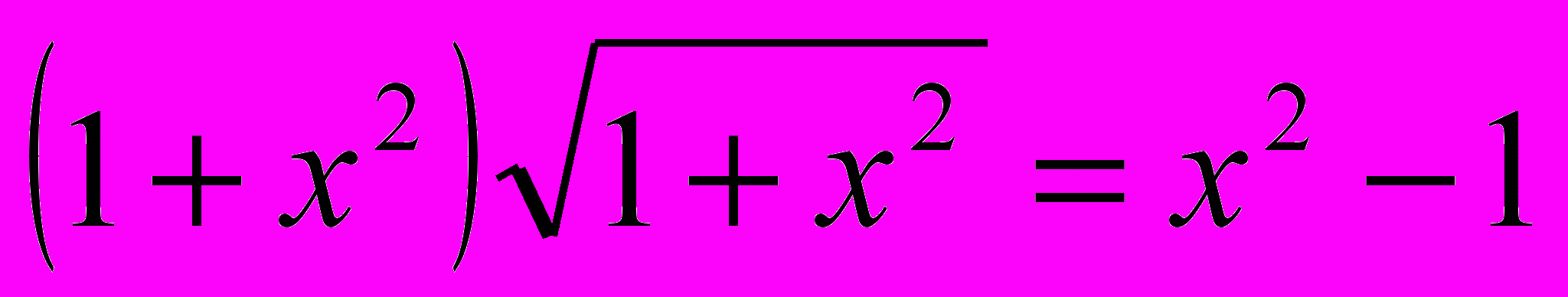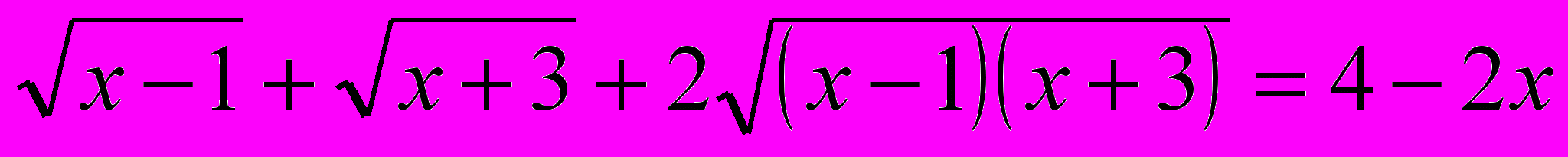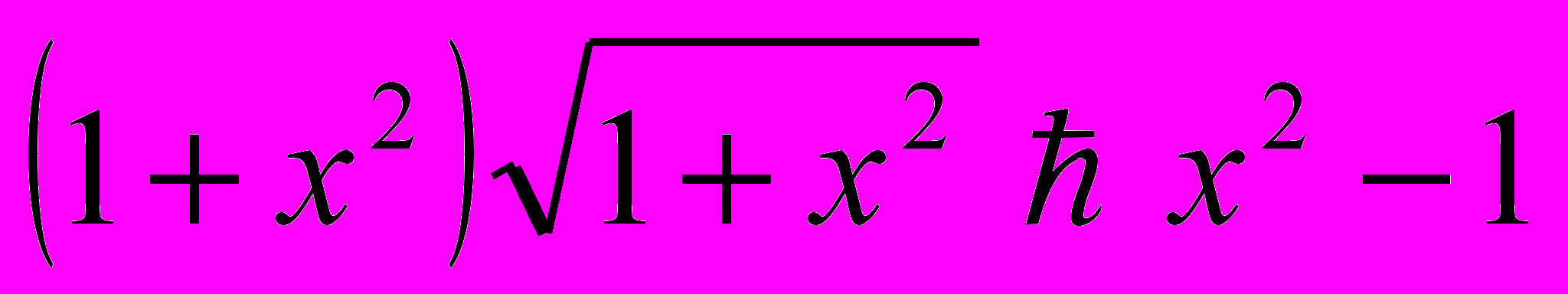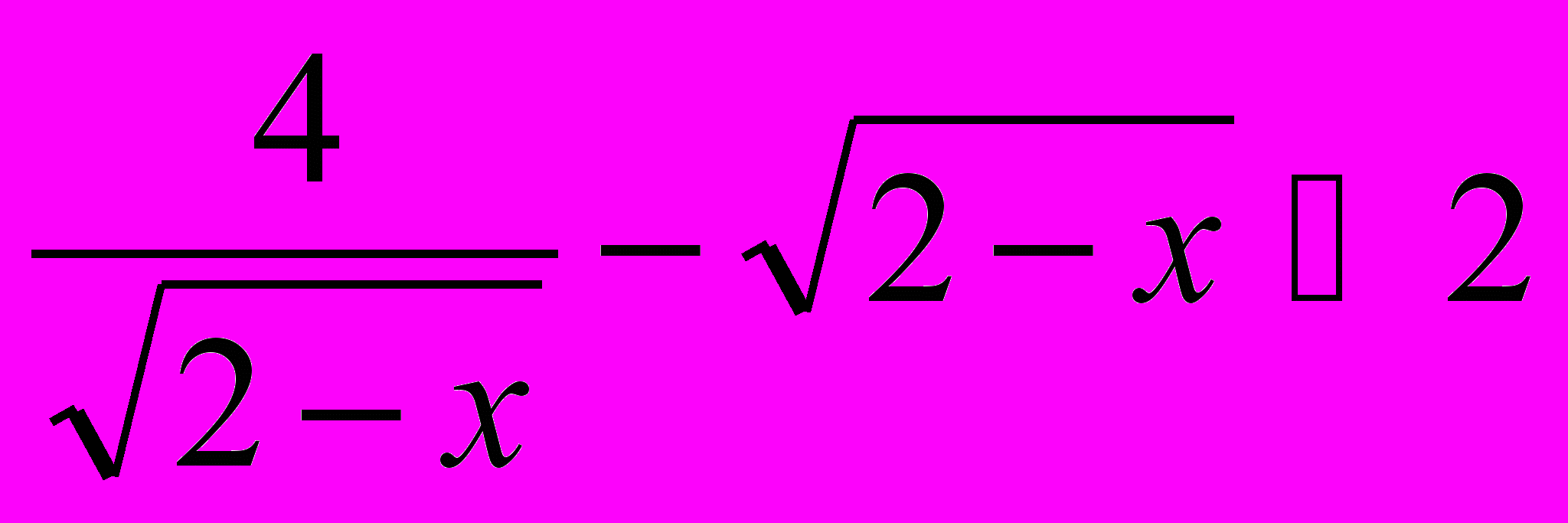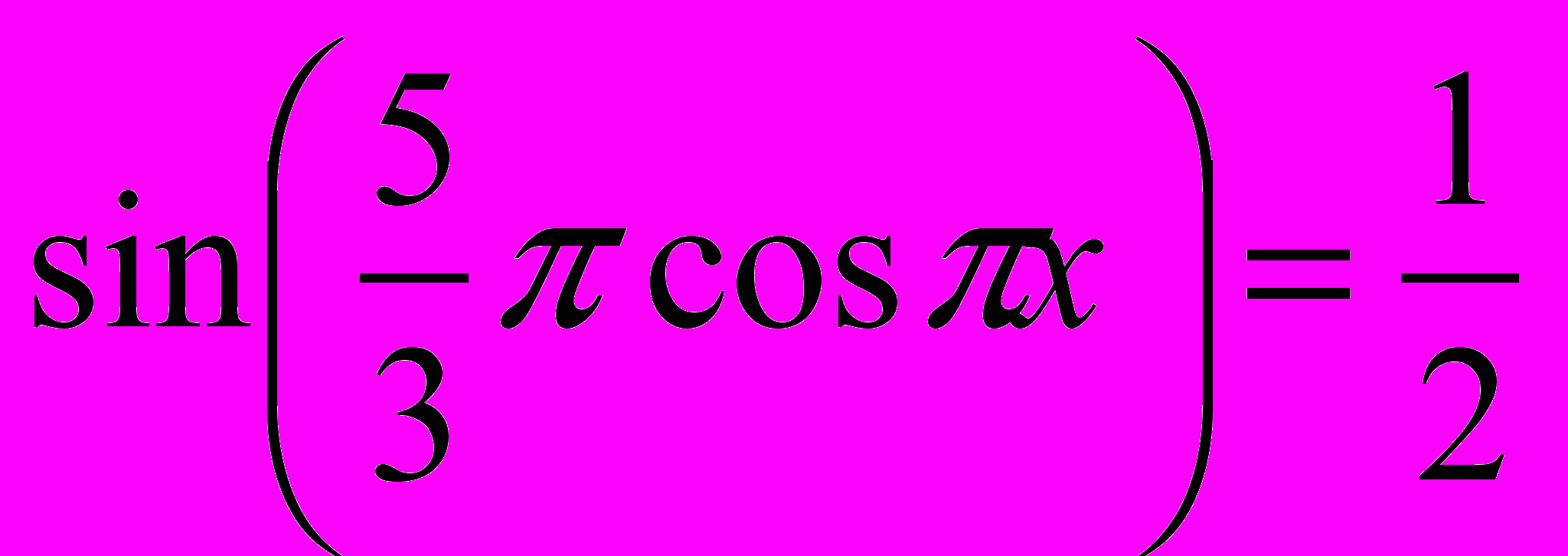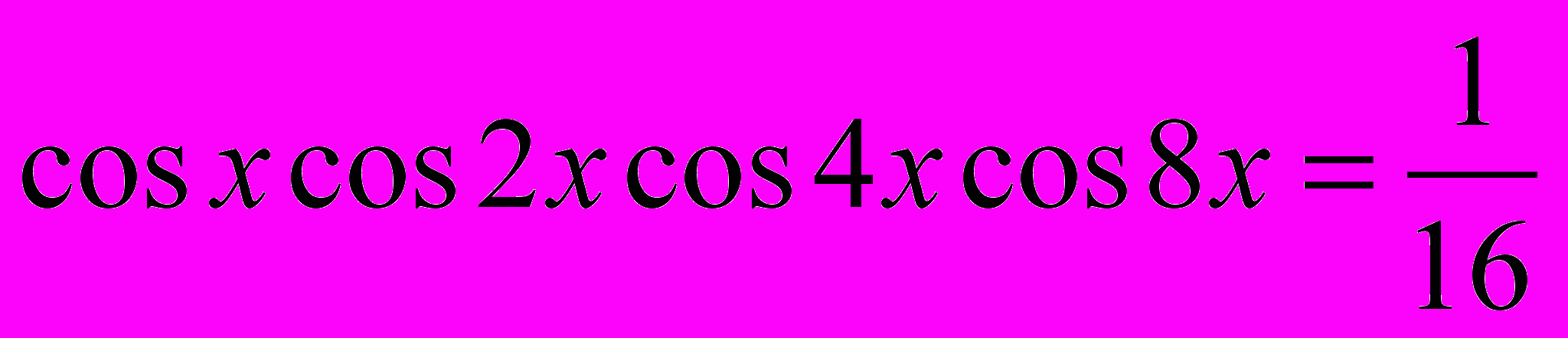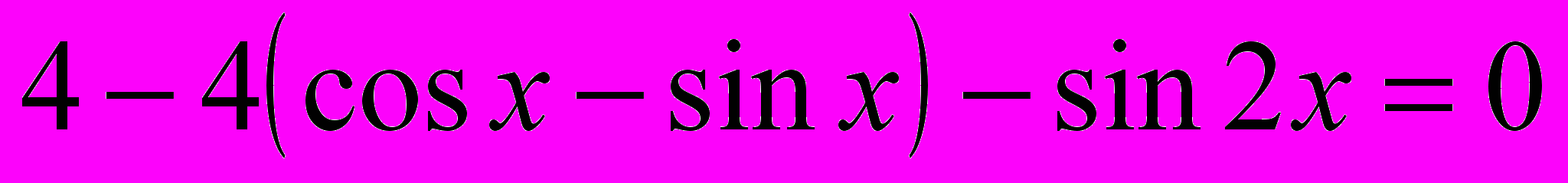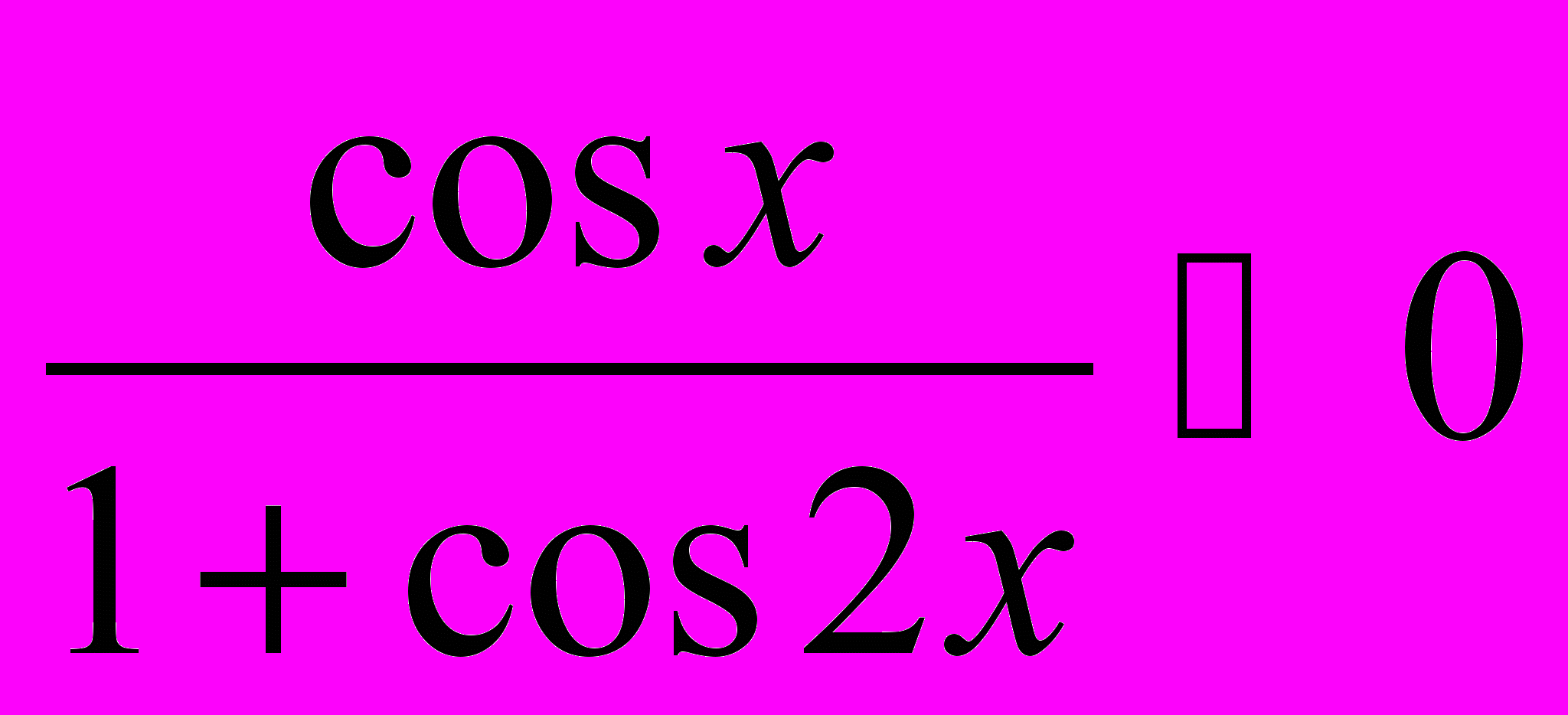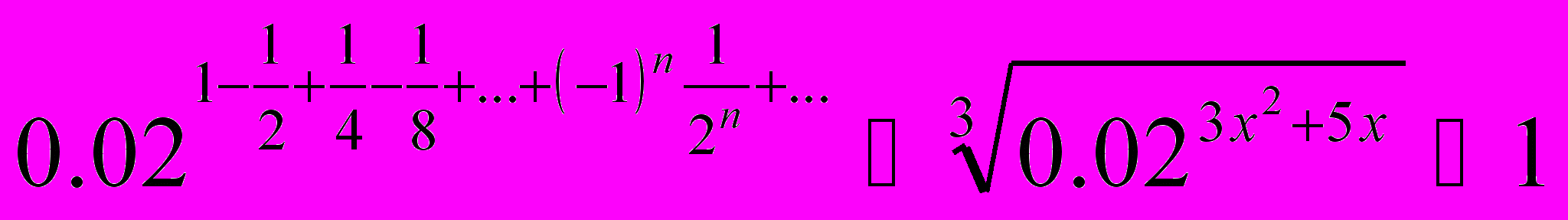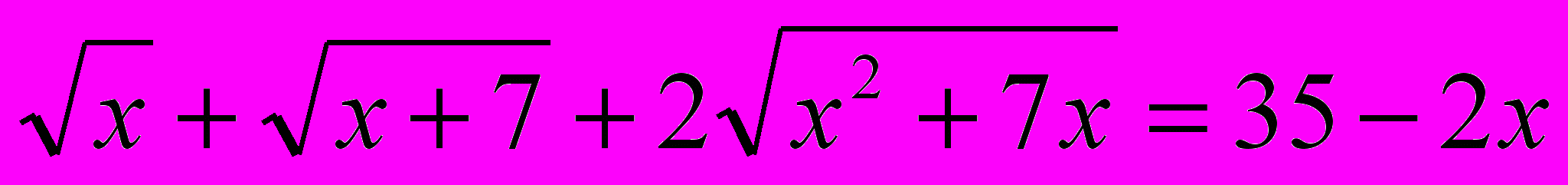Рабочая учебная программа по дисциплине «Практикум по решению задач по математике» для ооп «050100. 62 Педагогическое образование» Профиль «Математика» по циклу Б3 профессиональный цикл, вариативная часть

Вид материала

Содержание

1. Пояснительная записка
Учебно - тематическое планирование
Аудиторные занятия
2.2. Учебно-тематический план заочной формы обучения
Аудиторные занятия
3. Содержание дисциплины
Коды компетенций
Содержание дисциплины
4. Самостоятельная работа И ОРГАНИЗАЦИЯ КОНТРОЛЬНО-ОЦЕНОЧНОЙ ДЕЯТЕЛЬНОСТИ
5. Требования к результатам освоения содержания дисциплины
6. Учебно-методическое и информационное
6.2. Информационное обеспечение дисциплины
7. Материально-техническое и дидактическое обеспечение дисциплины
8. СВЕДЕНИЯ ОБ авторЕ программы

Подобный материал:

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Уральский государственный педагогический университет»
Математический факультет

Кафедра теории и методики обучения математике

РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА

по дисциплине «Практикум по решению задач по математике»

для ООП «050100.62 – Педагогическое образование»

Профиль «Математика»

по циклу Б3 – профессиональный цикл,

вариативная часть

Очная форма обучения

Курс – 4

Семестр – 7,8

Объем в часах всего – 144

в т.ч.: лекции – 24

практические занятия – 45

лабораторные занятия –

самостоятельная работа – 75

Экзамен –– 8 семестр

Зачет –7 семестр

Заочная форма обучения

Курс – 3, 4

Семестр – 6,7,8

Объем в часах всего – 144

в т.ч.: лекции –

практические занятия – 26

лабораторные занятия –

самостоятельная работа – 118

Экзамен – 7

Контрольная работа – 7

Екатеринбург 2011

Рабочая учебная программа по дисциплине

«Практикум по решению задач по математике»

ГОУ ВПО «Уральский государственный педагогический университет»

Екатеринбург, 2011. – 16 с.

Составитель:

Никулина Г.Н., старший преподаватель кафедры теории и методики обучения математике, математический факультет УрГПУ

Рабочая учебная программа обсуждена на заседании кафедры теории и методики обучения математике УрГПУ

Протокол от ________ г. № _.

Зав. кафедрой И.Г. Липатникова.

Согласовано с методической комиссией математического факультета

Председатель методической комиссии И.Н. Семенова

Декан математического факультета В.П. Толстопятов.

1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Практикум по решению задач по математике является базой практических знаний и умений, на основе которых будут раскрываться методические аспекты преподавания конкретных тем школьного курса математики. Поэтому основное внимание в программе курса отведено тем разделам, которые тесно связаны со школьной математикой.

Основной целью курса является подготовка студентов к преподаванию элементарной алгебры в средней школе. Преподавание происходит на базе обучения методам и приёмам решения задач с параметрами, требующих высокой логической и операционной культуры, развивающих научно – теоретическое и алгоритмическое мышление студентов. Тематика лекций и практических занятий не выходит за рамки основного курса школьной математики, но уровень их сложности – повышенный, существенно превышающий обязательный. Особое место занимают вопросы, требующие от студентов нестандартного подхода, умения анализировать, моделировать и систематизировать математические знания.

Основная систематизация рассматриваемых методов решения проведена не по конкретным примерам задач по виду функций, входящих в уравнение, неравенство или систему, а по особенностям математической деятельности, необходимой для решения задачи. Тем самым в рамках курса возможен большой охват материала.

Программа по дисциплине «Практикум по решению задач по математике» ориентирована на становление творческой индивидуальности будущего педагога, осмысление и интерпретацию основных методов решения уравнений, неравенств и их систем.

Цели курса

сформировать профессиональные компетенции у студентов на основе обучения их основным методам решения уравнений, неравенств и их систем;
создать студентам условия для развития самопознания, самоопределения, самовыражения, самоутверждения, самооценки, самореализации;
сформировать у студентов в процессе обучения дисциплине такие качества личности, как мобильность, умение работать в коллективе, принимать решения в стандартных и нестандартных ситуациях, ответственность, толерантность.

Задачи курса

систематизировать знания, необходимые для решения уравнений, неравенств и их систем;
выделить основные методы решения уравнений, неравенств и их систем;
развить у студентов умения осуществлять анализ собственной будущей профессиональной деятельности, осмысливать способы достижения результатов своей деятельности, анализировать затруднения, возникающие в процессе учебно-познавательной деятельности;
сформировать у студентов способности к самостоятельному определению своей готовности к восприятию новой структурной единицы учебного процесса, отслеживанию роста профессионально личностных качеств на протяжении всего курса.

«Практикум по решению задач по математике» является дисциплиной общепрофессиональной подготовки и связан с такими дисциплинами как педагогика, информационные технологии в обучении математике.

Содержательный и процессуальный компоненты дисциплины предполагают реализацию преемственности знаний студентов по методике обучения и воспитания в математическом образовании, элементарной математике, дидактике.

Процесс изучения дисциплины направлен на формирование следующих компетенций:

ОК – 4: использовать знания о современной естественно-научной картине мира в образовательной и профессиональной деятельности, применять методы математической обработки информации теоретического и экспериментального исследований.

Знать:

- основные методы решения уравнений и неравенств.

Уметь:

- осуществлять анализ выбора нужного метода решения;

- выделять главное;

- интерпретировать метод к данной задаче.

Владеть:

- навыками решения уравнений, неравенств и их систем;

- навыками алгебраических преобразований;

- навыками применения математических формул.

ОК – 6: логически верно воспроизводить устную и письменную речь.

Знать:

- основы математических теорий;

- основы формулировки математических утверждений;

Уметь:

- осуществлять анализ данного математического текста;

- выделять главное в математических рассуждениях.

Владеть:

- навыками решения основных видов уравнений, неравенств и их систем.

ОПК – 3: владеть основами речевой профессиональной культуры.

Знать:

- требования к текстам математических задач;

- современные подходы к формулировкам математических заданий;

- классификации математических заданий.

Уметь:

- грамотно излагать математическую информацию;

- доходчиво интерпретировать данный математический текст.

Владеть:

- умением грамотного изложения математической информации.

Курс «Практикум по решению задач по математике» включает лекции, лекции-исследования, лекции-дискуссии, практические занятия. Общая трудоемкость дисциплины составляет 4 зачетные единицы.

2. УЧЕБНО - ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

2.1. Учебно-тематический план очной формы обучения

№ п/п	Наименование раздела, темы	Всего трудо-емкость	Аудиторные занятия			Самос-тоя- тель- ная работа
№ п/п	Наименование раздела, темы	Всего трудо-емкость	Всего	Лек-ции	Прак-тиче-ские	Самос-тоя- тель- ная работа
1.	Уравнения. Основные методы решения уравнений	16	6	2	4	10
2.	Обобщенные методы решения уравнений	16	8	2	6	8
3.	Неравенства. Основные методы решения неравенств	14	6	2	4	8
4.	Неравенства повышенной трудности	22	10	4	6	12
5.	Системы и совокупности уравнений и неравенств	16	8	4	4	8
6.	Тригонометрические функции и их свойства	10	4	2	2	6
7.	Тригонометрические уравнения и неравенства	26	14	4	10	12
8.	Нестандартные методы решения тригонометрических уравнений и неравенств	24	13	4	9	11
	Итого:	144	69	24	45	75

2.2. Учебно-тематический план заочной формы обучения

№ п/п	Наименование раздела, темы	Всего трудо-емкость	Аудиторные занятия			Самос-тоя- тель- ная работа
№ п/п	Наименование раздела, темы	Всего трудо-емкость	Всего	Лек-ции	Прак-тиче-ские	Самос-тоя- тель- ная работа
1.	Уравнения. Основные методы решения уравнений	16	2	-	2	14
2.	Обобщенные методы решения уравнений	16	4	-	4	12
3.	Неравенства. Основные методы решения неравенств	14	2	-	2	12
4.	Неравенства повышенной трудности	22	4	-	4	18
5.	Системы и совокупности уравнений и неравенств	16	2	-	2	14
6.	Тригонометрические функции и их свойства	10	2	-	2	8
7.	Тригонометрические уравнения и неравенства	26	6	-	6	20
8.	Нестандартные методы решения тригонометрических уравнений и неравенств	24	4	-	4	20
	Итого:	144	26	-	26	118

3. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ

№ п/п	Наименование раздела (темы)	Содержание раздела	Коды компетенций
1.	Уравнения. Основные методы решения уравнений	Понятие уравнения. Алгебраические уравнения. Иррациональные уравнения. Показательные уравнения. Логарифмические уравнения. Равносильность уравнений. Методы решения уравнений.	ОК-4, ОК-6, ОПК-3
2.	Обобщенные методы решения уравнений	Обобщенные методы решения уравнений. Уравнения повышенной трудности. Нестандартные методы решения уравнений.	ОК-4, ОК-6, ОПК-3
3.	Неравенства. Основные методы решения неравенств	Понятие неравенства. Основные методы решения неравенств. Иррациональные неравенства. Показательные и логарифмические неравенства.	ОК-4, ОК-6, ОПК-3
4.	Неравенства повышенной трудности	Неравенства повышенной трудности, входящие в школьный курс математики. Неравенства повышенной трудности, входящие в варианты олимпиадных заданий по математике различных уровней.	ОК-4, ОК-6, ОПК-3
5.	Системы и совокупности уравнений и неравенств	Понятие системы и совокупности уравнений и неравенств. Основные методы решения систем и совокупностей уравнений и неравенств. Нестандартные методы решений систем и совокупностей уравнений и неравенств.	ОК-4, ОК-6, ОПК-3
6.	Тригонометрические функции и их свойства	Определение тригонометрических функций. Свойства тригонометрических функций.	ОК-4, ОК-6, ОПК-3
7.	Тригонометрические уравнения и неравенства	Определение тригонометрических уравнений и неравенств. Основные методы решения тригонометрических уравнений и неравенств. Классификация тригонометрических уравнений по методам их решения.	ОК-4, ОК-6, ОПК-3
8.	Нестандартные методы решения тригонометрических уравнений и неравенств	Нестандартные методы решения тригонометрических уравнений и неравенств. Метод интервалов в решении тригонометрических уравнений и неравенств.	ОК-4, ОК-6, ОПК-3

Все лекционные и практические занятия реализуются в активной и интерактивной формах.

Темы лекционных занятий

Уравнения. Основные методы решения уравнений.
Обобщенные методы решения уравнений.
Неравенства. Основные методы решения неравенств.
Неравенства повышенной трудности.
Системы и совокупности уравнений и неравенств.
Тригонометрические функции и их свойства.
Тригонометрические уравнения и неравенства.
Нестандартные методы решения тригонометрических уравнений и неравенств.

Вопросы для контроля и самоконтроля

Сформулируйте определение равносильных уравнений.
Дайте характеристику основных методов решений уравнений различных видов.
Дайте характеристику основных методов решений неравенств различных видов.
Назовите наиболее эффективные методы решения уравнений различных видов.
Назовите наиболее эффективные методы решения неравенств различных видов. Соотнесите, составьте таблицу (схему)
Охарактеризуйте задания, связанные с решением уравнений, включенных в варианты ГИА и ЕГЭ.
Охарактеризуйте задания, связанные с решением неравенств, включенных в варианты ГИА и ЕГЭ.
Охарактеризуйте преимущество использования метода интервалов для решения тригонометрических неравенств.
Приведите примеры характерных ошибок при решении различных видов уравнений.
Приведите примеры характерных ошибок при решении различных видов неравенств.
Укажите принципиальное отличие в выборе ответа при решении систем и совокупностей уравнений и неравенств.

Перечень тем занятий, реализуемых в активной и интерактивной формах

№	Содержание дисциплины	Формы обучения	Методы обучения	Технология обучения
1	Уравнения. Основные методы решения уравнений	Лекция-беседа, семинар с элементами проблемности, самостоятельная работа	Интерактивные методы, коммуникативный познавательный, преобразовательный, проблемный	Деятельностного подхода, дифференцированного обучения, рефлексивного подхода
2	Обобщенные методы решения уравнений	Лекция-исследование, практика-исследование, самостоятельная работа	Моделирование, интерактивные методы, познавательный, систематизирующий	Деятельностного подхода, дифференцированного обучения, рефлексивного подхода
3	Неравенства. Основные методы решения неравенств	Лекция-дискуссия, семинар с элементами проблемности, самостоятельная работа	Познавательный, преобразовательный, систематизирующий, проблемный, интерактивные методы	Деятельностного подхода, дифференцированного обучения, рефлексивного подхода
4	Неравенства повышенной трудности	Лекция-дискуссия, практика-исследование	Коммуникативный, познавательный, проблемный, интерактивные методы	Деятельностного подхода, дифференцированного обучения, рефлексивного подхода
5	Системы и совокупности уравнений и неравенств	Проблемная лекция	Коммуникативный познавательный, преобразовательный, систематизирующий, проблемный	Деятельностного подхода, дифференцированного обучения, рефлексивного подхода
6	Тригонометрические функции и их свойства	Лекция-дискуссия, семинар с элементами проблемности, самостоятельная работа	Познавательный, преобразовательный, систематизирующий, проблемный, интерактивные методы	Деятельностного подхода, дифференцированного обучения, рефлексивного подхода
7	Тригонометрические уравнения и неравенства	Лекция-дискуссия, семинар с элементами проблемности, самостоятельная работа	Познавательный, преобразовательный, систематизирующий, проблемный, интерактивные методы	Деятельностного подхода, дифференцированного обучения, рефлексивного подхода
8	Нестандартные методы решения тригонометрических уравнений и неравенств	Лекция-дискуссия, семинар с элементами проблемности, самостоятельная работа	Познавательный, преобразовательный, систематизирующий, проблемный, интерактивные методы	Деятельностного подхода, дифференцированного обучения, рефлексивного подхода

4. Самостоятельная работа И ОРГАНИЗАЦИЯ КОНТРОЛЬНО-ОЦЕНОЧНОЙ ДЕЯТЕЛЬНОСТИ

Перечень заданий для самостоятельной работы

1. Изучите вопросы, связанные с изучением различных видов уравнений, неравенств и их систем в школьном курсе математики.

2. Подготовьте различные варианты заданий по решению уравнений, неравенств и их систем для самостоятельных работ учащихся математических классов, гуманитарных классов.

3. Разработайте задания для подготовки учащихся к сдаче ГИА и ЕГЭ.

4. Проанализируйте статьи по проблемам проведения ГИА и ЕГЭ, опубликованные в периодической печати. Дайте анализ задачам, предлагаемым в вариантах ГИА и ЕГЭ.

Контрольные работы для студентов заочной формы обучения

Для заданий контрольной работы охарактеризовать основные методы решения и провести анализ возможных прогнозируемых ошибок у учащихся при решении данных задач (приведен один из вариантов контрольной работы).

Решить уравнения.

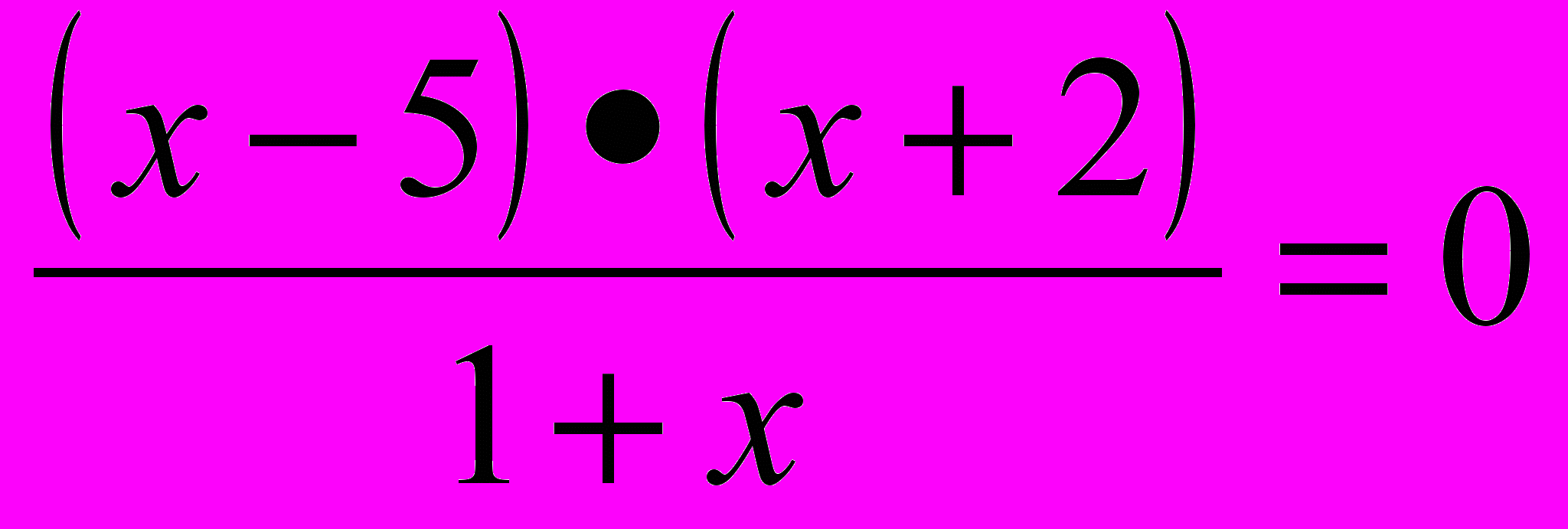
Решить неравенства.
Решить системы.
Решить уравнения.
Построить график функции.

Контрольные работы для студентов очной формы обучения

Для заданий контрольной работы охарактеризовать основные методы решения и провести анализ возможных прогнозируемых ошибок у учащихся при решении данных задач (приведен один из вариантов контрольной работы).

Решить систему.
Решить уравнения.
Решить неравенства.
Решить уравнения.

Задания для зачета

Назовите наиболее рациональный метод решения задания.

5. ТРЕБОВАНИЯ К РЕЗУЛЬТАТАМ ОСВОЕНИЯ СОДЕРЖАНИЯ ДИСЦИПЛИНЫ

Студент, изучивший дисциплину, должен овладеть следующими компетенциями:

ОК – 4: использовать знания о современной естественно-научной картине мира в образовательной и профессиональной деятельности, применять методы математической обработки информации теоретического и экспериментального исследований.

Знать:

- основные методы решения уравнений, неравенств и их систем;

- основные методы решения тригонометрических уравнений, неравенств и их систем.

Уметь:

- осуществлять анализ выбора нужного метода решения;

- выделять главное;

- интерпретировать метод к данной задаче.

Владеть:

- навыками решения уравнений и неравенств;

- навыками алгебраических преобразований;

- навыками применения математических формул.

ОК – 6: логически верно воспроизводить устную и письменную речь.

Знать:

- основы математических теорий;

- основы формулировки математических утверждений;

Уметь:

- осуществлять анализ данного математического текста;

- выделять главное в математических рассуждениях.

Владеть:

- навыками решения основных видов уравнений и неравенств.

ОПК – 3: владеть основами речевой профессиональной культуры.

Знать:

- требования к текстам математических задач;

- современные подходы к формулировкам математических заданий;

- классификации математических заданий.

Уметь:

- грамотно излагать математическую информацию;

- доходчиво интерпретировать данный математический текст.

Владеть:

- умением грамотного изложения математической информации.

Студент должен знать:

основные этапы решения различных видов равнений и неравенств;
сущность основных методов решения конкретных уравнений, неравенств и их систем;
пути поиска решения нестандартных задач.

Студенты должны уметь:

выполнять анализ решения задачи;
применять основные методы для поиска решения задач;
решать различные типы задач;
находить нестандартные подходы к решению задач.

6. УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ
ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ

6.1. Рекомендуемая литература

Вишенский, В. О. Задачи по математике / В.О. Вишенский, М.О. Перестюк, А.М. Самойленко. – Киев: Высшая школа, 2005 – 264 с.
Габович, И. Г. Сколько корней имеет уравнение? / И.Г. Габович, П.И. Горнштейн // Квант. – 2000 - №3 – с. 43 – 46.
Говоров, В. М. Сборник конкурсных задач по математике (с методическими указаниями и решениями): Учеб. пособие / В.М. Говоров, П.Т. Дыбов, Н.В. Мирошин, С.Ф. Смирнова. – 2-е издание – М.: Наука, 2010. – 384 с.
Голубев, В. И. О параметрах – с самого начала / В.И. Голубев, А.М. Гольдман, Г.В. Дорофеев // Репетитор. – 2007. – №2 – с. 3 – 13.
Голубев, В. И. Абсолютная величина числа в конкурсных экзаменах по математике / В.И. Голубев. – Львов, 2000. – 96 с. – (Квантор №8).
Горделадзе, Ш. Х. Сборник конкурсных задач по математике. 3-е издание / Ш.Х. Горделадзе, М.М. Кухарчук, Ф.П. Яремчук. – Киев: Высшая школа, 2010. – 328 с.
Горнштейн, П. И. Тригонометрия помогает алгебре / П.И. Горнштейн // Квант. – 2000. - №5. – С. 68 – 70.
Горнштейн, П. И. Необходимые условия в задачах с параметрами / П.И. Горнштейн, В.Б. Полонский, М.С. Якир // Квант – 2000. – № 11. – С. 44 – 49.
Дорофеев, Г. В. О задачах с параметрами, предлагаемых на вступительных экзаменах в вузы / Г.В. Дорофеев // Математика в школе. – 2009. - №4. – С. 36 – 40.
Дорофеев, Г. В. Квадратный трёхчлен в задачах / Г.В. Дорофеев. – Львов, 2000. – 103 с. (Квантор, №2).
Дорофеев, Г. В. Пособие по математике для поступающих в вузы / Г.В. Дорофеев, М.К. Потапов, Н.Х. Розов. – М.: Наука, 2006. – 638 с.
Дорофеев, Г. В. Как расположены корни трёхчленов? / Г.В. Дорофеев // Квант. – 2000. - № 7. – С. 45 – 49.
Дорофеев, Г. В. Системы двух линейных уравнений с двумя неизвестными / Г.В. Дорофеев // Квант. – 2000. - № 9. – С. 63 – 67.
Дорофеев, Г. В. Решение задач, содержащих параметры / Г.В. Дорофеев, В.В. Затавкай. – М.: Науч. – пед. об – ние «Перспектива», 2010. – Ч.2. – 38 с.
Марков, В. К. Метод координат и задачи с параметрами / В.К. Марков. – М.: изд – во Моск. ун – та, 2008. – 146 с.
Нестеренко, Ю. В. Задачи вступительных экзаменов по математике / Ю.В. Нестеренко, С.Н. Олехник, М.К. Потапов. – М.: Наука, 2006. – 512 с.
Планирование учебного материала для IX класса с углублённым изучением математики: Метод. рекомендации. / М. Г. Галицкий, А. М. Гольдман, Л. И. Звавич. – М.: Б. И., 2009 – 172 с.
Пятьсот четырнадцать задач с параметрами / под ред. С.А.Тынянкина – Волгоград: Б. И., 2010 – 160 с.
Сборник задач по математике для поступающих в вузы: Учеб. пособие / П. Т. Дыбов, А. И. Забоев, А. С. Иванов, Д. Ф. Калиниченко, Н. В. Шолохов; под редакцией А. И. Прилепко. – М.: Высшая школа, 2007 – 239 с.
Цыпкин, А. Г. Справочник по методам решения задач по математике для средней школы / А.Г. Цыпкин, А.И. Пинский. – 2-е издание, перераб. и доп. – М.: Наука, 2009. – 576 с.
Шарыгин, И. Ф. Факультативный курс по математике. Решение задач: Учеб. пособие для 10-х классов средней школы / И.Ф. Шарыгин. – М.: Просвещение, 2008. – 384 с.
Шарыгин, И. Ф. Факультативный курс по математике. Решение задач: Учеб. пособие для 11 класса средней школы / И.Ф. Шарыгин, В.И. Голубев. – М.: Просвещение, 2007. – 384 с.
Ястребинецкий, Г. А. Задачи с параметрами / Г.А. Ястребинецкий. – М.: Просвещение, 2006. – 128 с.

6.2. Информационное обеспечение дисциплины

Презентации по темам курса:

1. Классификация основных методов решения уравнений.

2. Классификация основных методов решения неравенств.

3. Основные методы решения тригонометрических уравнений.

4. Основные методы решения тригонометрических неравенств.

7. Материально-техническое и дидактическое обеспечение дисциплины

Учебно-методические пособия:

Нестеренко Ю.В. Задачи вступительных экзаменов по математике / Ю.В. Нестеренко, С.Н. Олехник, М.К. Потапов. – М.: Наука, 2006. – 512 с.
Кузнецова Л.В. Сборник заданий для подготовки к государственной итоговой аттестации в 9 классе / Л.В. Кузнецова, С.Б. Суворова, Е.А. Бунимович, Т.В. Колесникова, Л.О. Рослова – М.: Просвещение, 2010. – 239 с.
Ляшко М.А. Сдаём ЕГЭ / М.А. Ляшко, С.А. Ляшко, О.В. Муравина – М.: Дрофа, 2011. – 151 с.

8. СВЕДЕНИЯ ОБ авторЕ программы

Никулина Грануш Норайровна

старший преподаватель кафедры теории и методики обучения математике Уральского государственного педагогического университета

рабочий телефон 371 – 45 – 97

РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА

по дисциплине «Практикум по решению задач по математике»

для ПрОП «050100.62 – Педагогическое образование»

Профиль: Математическое образование

по профессиональному циклу Б3.В.00 «Курсы по выбору студента»

Подписано в печать Формат 60х84/16

Бумага для множительных аппаратов. Усл. печ. л. .

Тираж экз. Заказ .

Уральский государственный педагогический университет.

620017 Екатеринбург, пр. Космонавтов, 26.

Blog

Содержание