Тема: Агрегированное планирование производства

Вид материала

Лабораторная работа

Содержание 2. Модели с квадратичной функцией затрат. Составляющие затрат. Затраты, связанные с приемом и увольнением. Затраты, связанные со сверхурочными работами и простоями. Построение модели. 2.2. Модификация модели ХММС. 2.3.Преимущества и недостатки моделей с квадратичной функцией затрат. 3. Модели для определения оптимального размера партии продукции (модели с постоянными затратами). 3.1. Модель для определения размера партии продукции (изделия) при отсутствии ограничений на его величину. Xt— объем продукции, производимой в течение t Т (Т+ 1)/2 таких последовательностей. 3. 3.2. Модель определения размера партии при наличии ограничений на его величину. N намного больше, чем число интервалов временя Т Найти при ограничениях Найти при ограничениях 3.3. Преимущества и недостатки моделей для определения размера партии продукции (изделий) 4. Модели с произвольной функцией затрат 4.1. Нелинейные аналитические модели. Найти при ограничениях Найти при ограничениях ... Полное содержание

Подобный материал:

• Планирование на предприятии (162 часа часов, курсовая работа, экзамен), 1133.77kb.
• Лекции по дисциплине «Организация и планирование производства» Тема Сущность и задачи, 76.87kb.
• Планирование на предприятии методическое пособие по выполнению курсовой работы для, 706.74kb.
• Темы курсовых работ по курсу «Организация производства на предприятиях отрасли (нефтяной, 44.8kb.
• Рабочая программа дисциплины организация и планирование производства направление подготовки, 218.59kb.
• Руководство по производству Раздел 1 Планирование производства свинины, 8767.45kb.
• Планирование как основа управления предприятием. Назначение, цели и горизонты планирования, 33.17kb.
• Организация и планирование сельскохозяйственного производства Специфика маркетинга, 46.25kb.
• Планирование и учет затрат и движение деталей в производстве 8 Экономический механизм, 876.54kb.
• Теоретические основы кадрового обеспечения в туризме, 54.44kb.

UNIVERSITATEA LIBERĂ INTERNAŢIONALĂ DIN MOLDOVA


Факультет экономических знаний


Бабаян Екатерина


тема: Агрегированное планирование производства

(Лабораторная работа)


Научный руководитель,

профессор: С.Максимилиан


Кишинёв, 2011


I - 3. Агрегированное планирование производства.


1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ АГРЕГИРОВАННОГО ПЛЛАНИРОВАНИЯ ПРОИЗВОДСТВА.

Математическое моделирование играет важную роль в процессе- принятия решений при прогнозированном планировании. В одной из работ, посвященных этой проблеме, перечисляются следующие задачи управления, при решении которых модели окапываются весьма эффективными:

- определение способа количественной оценки показателей и использование неосознанных принципов, которые обычно слу­чайно и эпизодически учитываются в решениях по планированию;

- проведение в регулярном порядке всестороннего анализа факторов, имеющих отношение к задачам планирования. Это ис­ключает возможность принятия решений на основании тривиаль­ных и поверхностных оценок;

- отведение каждому решению по планированию соответствую­щего места в установленной последовательности решений и кор­ректировка ошибок первоначального прогноза, осуществляемая с помощью механизма обратной связи, включенного в систему выбора вариантов решения;

- изменение установившейся практики принятия решении для обеспечения большей свободы действий, в особенности при воз­никновении чрезвычайных ситуаций.

Рассмотрим различные типы моделей агрегированного плани­рования, используя классификацию этих моделей в соответствии с предположениями о структуре составляющих затрат.

1.1. Модели с линейной функцией затрат

При разработке первых моделей систем агрегированного пла­нирования предполагалось, что затраты линейно зависят от управ­ляющих переменных модели. В результате этого предположения такие модели могли быть использованы для решения довольно узкого круга задач. Поскольку, однако, оказалось, что нелиней­ные выпуклые функции затрат могут быть с любой степенью точ­ности аппроксимированы кусочно-линейными функциями, то область применения моделей такого типа существенно расшири­лась. Подобные модели и сегодня находят широкое применение, что объясняется возможностью использования эффективных вы­числительных методов, разработанных для решения задач линей­ного программирования.

Рассмотрим два основных типа линейных моделей.

1.2. Модель планирования производства с постоянным фондом рабочей силы

Если предприятие имеет постоянный фонд рабочей силы, то, следовательно, объем производства может меняться только за счет использования сверхурочного времени и «поглощение» ко­лебаний спроса путем приема и увольнения невозможно. Для фор­мального математического описания такой системы используем в качестве параметров модели:

- затраты на производство одной единицы продукции i-го типа в течение t-гo интервала времени — v_it;

- затраты на храпение одной единицы продукции i-го типа в течение t -го интервала времени — с_и,

- стоимость одного человеко-часа трудозатрат штатного сотрудника в течение t-гo интервала времени — r_it,

- стоимость одного человеко-часа сверхурочной работы в те­чение t-го интервала времени – о_t;

а в качестве переменных модели:

- число единиц продукции i-гo типа, производимой в течение t-гo интервала времени — X_it;

- число единиц продукции i-го типа, которое необходимо иметь в запасе к концу t-гo интервала времени — I_it,

- количество человеко-часов постоянных сотрудников в те­чение t-гo интервала времени — W_t;

- количество человеко-часов сверхурочной работы в течение t-гo интервала времени — O_t.

Тогда задачу планирования можно сформулировать как мини­мизацию суммы затрат на производство продукции, хранение запасов, затрат, связанных с оплатой труда постоянных сотруд­ников, включая и сверхурочную работу, т. е.

найти:




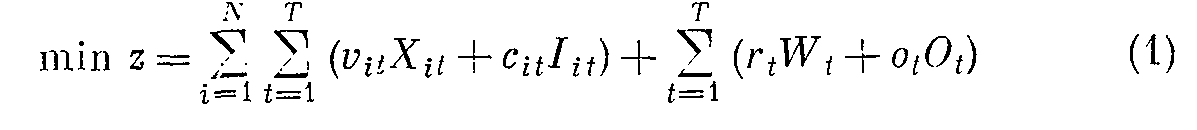
при ограничениях:







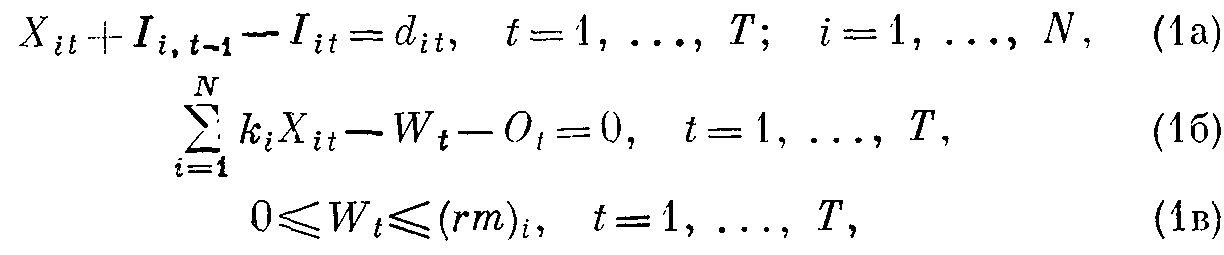
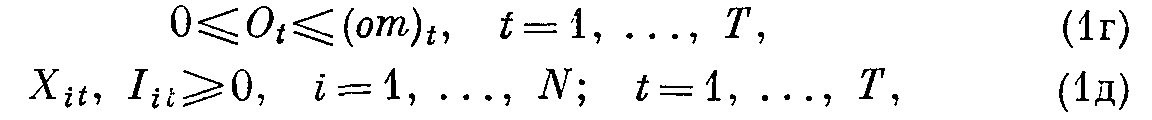
где d_ik — спрос на продукцию i-гo типа в течение t-го интервала времени; k_i - количество человеко-часов, необходимых для про­изводства единицы продукции i-гo типа; (rm)_t — общее количе­ство человеко-часов трудозатрат штатных сотрудников в течение t-го интервала времени, (om)_t — общее количество человеко-ча­сов сверхурочного времени в течение t-гo интервала времени, I_io — уровень начальных запасов продукции i-гo типа, W₀ — число постоянных сотрудников, Т — период планирования, N — общее число наименований типов продукции.

Если предельные затраты v_it па производство одной единицы продукции i-гo тина не зависят от времени, то член v_itX_it можно но учитывать, так как общее количество продукции каждого типа фиксировано. Аналогично, если величина W_t не зависит от времени, то член r_tW_t можно исключить из выражения (1).

Ограничение (1а) представляет собой уравнение баланса по количеству производимой продукции и уровню запасов при ус­ловии детерминированного спроса на каждый тип продукции в каждый заданный интервал времени. Одним из способов учета неопределенности прогноза спроса является определение для каж­дого заданного интервала времени минимального уровня резерв­ного запаса, т. е. введение ограничения вида I_it>= ss_it, где ss_it — резервный (буферный) запас продукции i-гo типа в течение вре­мени t^l). Следует заметить, что ограничения (1а и 1д) означают отсутствие задолженности по выполнению заказов в течение t-го интервала времени.

Ограничение-равенство (16) определяет допустимое количест­во трудовых ресурсов, которые могут быть использованы для вы­пуска продукции i-гo типа в каждый заданный интервал времени, причем это — единственное ограничение на резервы производства. Если сохранить предположение о линейной зависимости затрат от управляющих переменных системы, то целевая функция будет учитывать не только трудовые, но и другие ресурсы производства.

Ограничения (1в, 1г), по существу, устанавливают нижний и верхний пределы человеко-часов трудозатрат штатных сотрудни­ков и сверхурочных работ для каждого заданного интервала вре­мени. Как уже было показано, учет неопределенности прогноза спроса приводит к введению ограничения I_it >=SSit. Если уровень запасов в конце периода планирования никак не ограничен, то решение, получаемое с помощью модели, всегда обеспечивает I_{it =} 0 для всех значений i. В тех случаях, когда полное исчерпание запасов по всем видам продукции нежелательно, в модель должны быть введены соответствующие ограничения на уровень запасов. Дополнительные ограничения должны быть введены и в тех случаях, когда потребности в складировании продукции не могут превышать некоторой заданной величины. Например, огра­ничение:



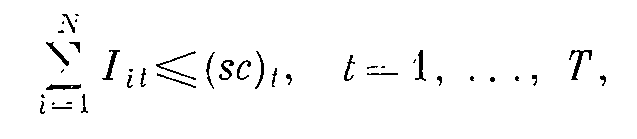
означает, что суммарный объем запасов всей продукции в каждый заданный интервал времени не может быть большим, чем общая емкость склада (sc)_t. В тех случаях, когда необходимо закрепить изготовление продукции за различными производственными еди­ницами ограниченной мощности, управляющие переменные выби­рают таким образом, чтобы получить соответствующие решения. Например, величина X _ict может означать число единиц продукции i-гo типа, производимой производственной единицей с в течение t- го интервала времени. Результат подобной замены (или преобра­зования) управляющих переменных необходимо программировать непосредственно в рамках общей модели.

Следует иметь в виду, что даже в случае очень простой модифи­кации рассматриваемой модели могут возникнуть существенные трудности, связанные с процессом вычисления, если не выполнена укрупненная классификация отдельных видов продукции, произ­водство которых планируется. Если предположить, что мы не бу­дем принимать во внимание ограничения (1 в-д), которые лишь устанавливают верхние и нижние пределы значений переменных, то все еще остается Т (N +1) существенных ограничений.

На сложных производствах общее число отдельных наимено­ваний изделий N может достигать нескольких тысяч. Например, если модель составлена для периода планирования, равного 12, и 5000 наименований изделий, то она должна содержать около 60 000 ограничений.

Это, естественно, превышает возможности линейного програм­мирования.

В большинстве случаев, однако, нерационально планировать распределение производственных ресурсов на таком уровне дета­лизации. Это объясняется следующими причинами. Во-первых, программы детального планирования должны принимать в рас­чет большое количество показателей технологии производства и системы сбыта, которые не могут быть включены в общую модель, так- как имеют явно выраженный качественный характер. Во-вто­рых, как уже отмечалось, многие результаты планирования, по­лученные с помощью модели, широко связаны с решением задач распределения ресурсов и, следовательно, чрезмерно подробная информация будет только затруднять процесс принятия решения, а не способствовать ему. В-третьих, прогнозы, основанные на агрегированной информации, являются более точными, чем прог­нозы, основанные на подробной информации. Поэтому обычно осуществляют укрупненную классификацию изделий. Критерии подобной классификации определяются структурой модели: еди­ницы продукции одной группы должны совместно формировать спрос d_it, иметь общие показатели затрат v_it c_it r_t, o_t и на изго­товление каждой единицы продукции должно затрачиваться одно и то же количество времени k_i. Принятые решения по агрегирован­ному планированию позволяют сформулировать ограничения, которым должен удовлетворять детальный план изготовления из­делий.

Рассмотренная модель, как и любая другая модель планирова­ния, требует определения периода планирования и разбиения его на интервалы, длительность которых не обязательно должна быть одинаковой. Для многих систем планирования целесообразно раз­бивать период планирования на интервалы различной длитель­ности, так как в начале периода мы располагаем более подробной информацией. Из-за неопределенности условий, в которых реали­зуются решения по планированию, последние обычно оказываются полностью реализованными лишь на начальном этапе планирова­ния. В конце каждого этапа появляется новая дополнительная информация, которая используется для корректировки модели и пересмотра плана для последующих этапов планирования. При формулировании задачи могут быть учтены ограничения, связан­ные с технологией производства, финансами, организационной структурой, рекламой, системой сбыта. Такая гибкость, хара­ктерная для подходов к решению задач линейного программирова­ния, позволяет довольно широко и эффективно использовать этот тип модели.

Простой вариант задачи линейного программирования с фик­сированным фондом рабочей силы, имеющей структуру транспорт­ной задачи, впервые был рассмотрен в работе [8].

1.3. Модель планирования с переменным фондом рабочей силы.

В тех случаях, когда «поглощение» колебаний спроса оказы­вается возможным за счет изменения фонда рабочей силы, по­следний становится переменной модели. Так как подобное изме­нение осуществляется в течение периода планирования путем приема и увольнения, то затраты, связанные с увольнением и прие­мом должны быть учтены в целевой функции. Кроме того, по­скольку модель допускает учет недостатка в ресурсах, то, следо­вательно, необходимо учитывать и издержки, связанные с невыпол­нением заказов.

В данном случае переменными модели являются: X _it- число единиц продукции i-го

ипа, производимой в течение i-гo интервала времени; W_t — количество человеко-часов работы штатных сотруд­ников в течение t-гo интервала времени: O_t — количество человеко-­часов сверхурочной работы в течение i-гo интервала времени; H_t — количество человеко-часов, зачисленных в штат организа­ции в течение t-гo интервала времени; F _t — количество неисполь­зованных человеко-часов в течение i-гo интервала времени из-за увольнения штатных сотрудников; 1_it+ — число единиц продукции i-гo типа, которую необходимо иметь в задаче к концу i-гo интер­вала времени; I_it- — число единиц продукции i-го типа, которой не хватает для удовлетворения спроса потребителя в конце i-гo интервала времени.

Используя перечисленные переменные модели и обозначения, принятые для предыдущей модели, определим следующие состав­ляющие затрат в течение времени t:

- переменная затрат производства V _it X_it;,

- затраты па храyение запасов C_itI_{it +,}

- затраты, связанные с задержкой выполнении заказов пот­ребителей b_itI_it-,

- затраты на содержание штатных сотрудников r_tW_t,

- затраты на оплату сверхурочной работы o_tO_t,

- затраты, связанные с приемом па работу, h_tH_t

- затраты, связанные с увольнением, f_tF_t-

В этом случае задача планирования формулируется следую­щим образом:

Найти




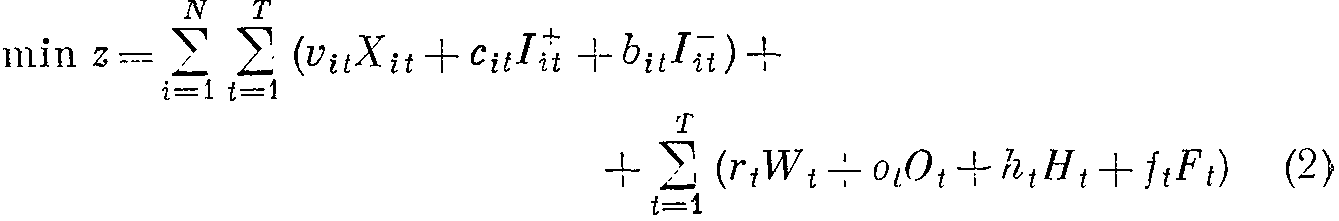
при ограничения:



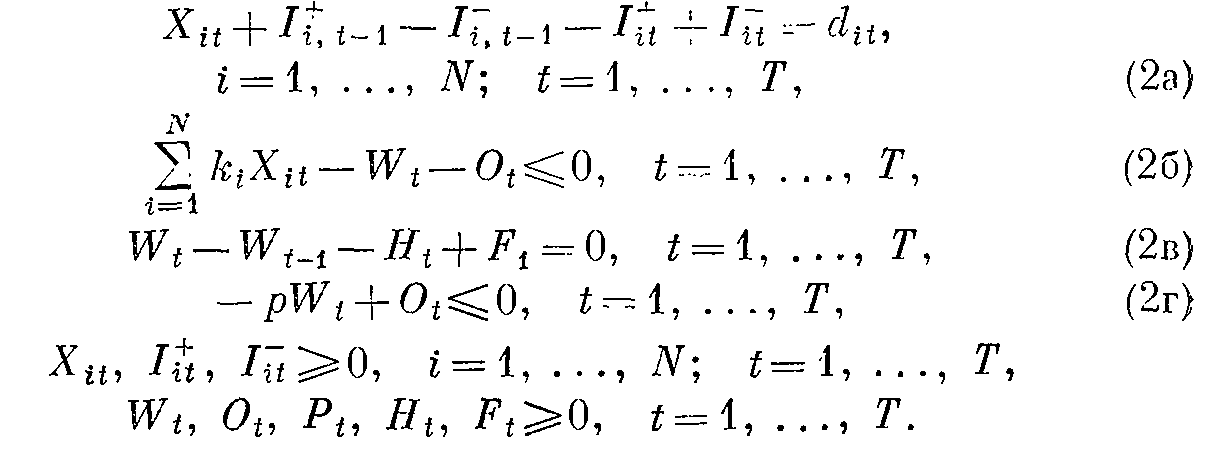
Ограничение (2а) представляет собой уравнение баланса по количеству произведенной продукции и уровню запасов. Заметим, что это уравнение эквивалентно уравнению баланса (1а), если при­нять, что I_i,t-1=I_{i, t-1} –I_i+,t-1 и I_it = I_it+-I_it-.

В рассматриваемой модели величина запаса I_t к концу t-го интер­вала времени может иметь положительное значение (It_t+ >0 оз­начает, что к концу i-гo интервала времени остается часть запаса) или отрицательное значение (I_it-> 0 означает, что к концу t-го интервала времени происходит накопление невыполненных зака­зов). Поскольку, однако, как величине It_t+ так и величине I_it- соответствуют определенные затраты, то эти переменные никогда не будут одновременно принимать положительного значения. Огра­ничения (2б) отражают тот факт, что объем производства лимити­руется фондом трудовых ресурсов.

Ограничения-равенства (2в) определяют изменение фонда рабо­чей силы в течение времени t, т. е. W_t — Wt-i = Н t — Ft. Фонд рабочего времени увеличивается, если H_t >0, и сокращается, если F_t >0. Аналогично предыдущему случаю величины H_t, F_t никогда не будут принимать одновременно положительных зна­чений в течение заданного интервала времени, так как им соот­ветствуют определенные затраты. Ограничение (2г) устанавливает верхний предел объема сверхурочной работы в течение времени t как функцию фонда рабочего времени штатных сотрудников, т. е. O_t <= pWt, где р — допустимая часть фонда рабочего времени штатных сотрудников для выполнения сверхурочных работ.

Модель такого типа впервые была рассмотрена в работе [33], а возможпые модификации модели — в работах [69, 87].

Липпман и др. [59] проанализировали вариант оптимального решения задачи планирования производства продукции одного типа в предположении, что функция затрат производства явля­ется выпуклой, функция затрат на храпение запасов — возрастаю­щей, а функция затрат, связанных с изменением фонда трудовых ресурсов, У-образной. Авторы работы [60] предложили для част­ного случая, когда все функции затрат линейны, а спрос либо монотонно убывает, либо возрастает, эффективный алгоритм ре­шения задачи.

Алгоритм представляет собой итеративную процедуру, которая начинается с предположения, что задано значение W_T, которое должно быть достигнуто к концу периода планирования. Это обес­печивает выбор оптимального решения для фиксированного зна­чения W_T и проверку решения на оптимальпость. Если оказыва­ется возможным улучшить решение, то алгоритм формирует новое значение W_T, обеспечивающее улучшенное решение, и процесс повторяется. Сходимость алгоритма гарантируется за конечное число итераций.

Если функция затрат линейна и функция спроса неубываю­щая, существует оптимальное решение, для которого выполняются условия:



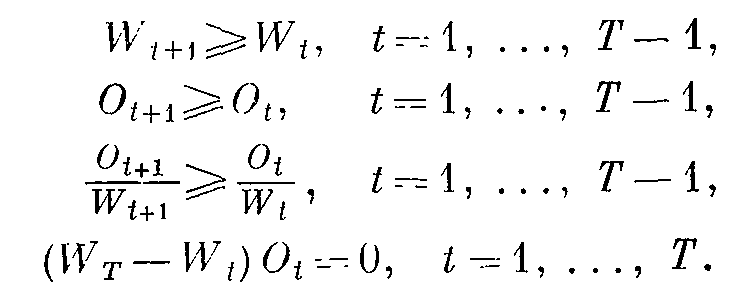
'(Этот результат постоянно используется в процессе вычисления.)

Юан [92] обобщил этот подход для решения задачи планирова­ния производства продукции различных типов.

В работах [2,38] рассматривается модель производства продук­ции одного типа с линейной функцией затрат, при этом целевая функция учитывает изменения уровня производства. Авторы про­анализировали качественные свойства оптимального решения и предложили простые методы поиска этого решения для случая, когда спрос является монотонно возрастающей функцией. Эта ра­бота была обобщена Джонсоном и Данцигом [46].

Модели линейного программирования легко могут быть приме­нены для планирования многоэтапного процесса производства. В работе [44] проведено исчерпывающее обсуждение многошаговых моделей линейного программирования, включающих множество технологий, множество источников снабжения, решения по выбору номенклатуры продукции, а также решения но организации многономенклатурного производства и распределения.

Преимущества и недостатки моделей с линейной функцией затрат

Основным преимуществом моделей с линейной функцией затрат является возможность «свести» задачи агрегированного планирования к задачам линейного программирования, решение которых можно быстро осуществить с помощью легкодоступных эффективных машинных программ. Подобные программы позволя­ют быстро и дешево получать решение для моделей с большим чис­лом переменных и ограничений. Кроме того, такие модели хорошо поддаются параметрическому анализу и анализу на чувствитель­ность, что может оказаться полезным в процессе агрегированного планирования. Так, информация о скрытых затратах может быть использована с целью определения благоприятных условий для расширения производственных мощностей, стратегий проникно­вения в сферу сбыта, целесообразности освоения производства но­вой продукции и т. д. Что касается предположения о линейной зависимости затрат от переменных, то, во-первых, основные состав­ляющие затрат, как правило, являются линейными функциями в интервале возможных изменений рассматриваемых переменных и, во-вторых, выпуклые сепарабельные функции могут быть аппро_Ксимированы кусочно-линейными. Более того, некоторые функции, имеющие на первый взгляд нелинейные характеристики, могут быть линеаризованы [33]. Однако модели лилейного програм­мирования не позволяют учесть неопределенности спроса, что, несомненно, является их существенным недостатком. В этой связи заслуживает внимания работа [19], в которой сообщается о поло­жительных результатах экспериментов по использованию моде­лей линейного программирования при достаточно высокой степени неопределенности в динамических условиях.


^ 2. МОДЕЛИ С КВАДРАТИЧНОЙ ФУНКЦИЕЙ ЗАТРАТ.

Если для решения задач агрегированного планирования произ­водственных мощностей используются модели с квадратичными функциями затрат, то решающие правила имеют линейную струк­туру. Это связано с тем, что в результате дифференцирования квадратичной функции получается линейная функция. Первая такая модель была разработана Холтом, Модильяни. Мазом и Саймоном (ХММС) [39] для случая полного агрегирования всех типов продукции в один класс. Это в свою очередь предполагает использование соответствующих сопоставимых единиц измере­ния продукции.

В модели ХММС используются в основном две переменные: объем выпуска агрегированной продукции в течение t-го интер­вала времени и фонд рабочей силы в течение i-гo интервала вре­мени W_t. Переменная I_t — уровень запаса i-гo интервала вре­мени — определяется с помощью церемонных Р_t и W_t и соответ­ствующих соотношений между этими переменными.

Оптимальное решающее правило определяет для каждого интервала времени необходимый объем производства агрегирован­ной продукции и величину фонда рабочей силы, минимизирующие квадратичную функцию затрат.

^ Составляющие затрат. Рассмотрим подробнее составляю­щие затрат, которые учитываются в квадратичной функции затрат.

Затраты на содержание персонала. Предполагается, что эти затраты линейно возрастают с увеличением фонда рабочей силы и описываются величиной c₁W_t +с₁₃, где с₁ и с₁₃ — коэффициенты затрат, которые определяются вне модели. Поскольку с₁₃ — кон­станта, то она может быть исключена из дальнейшего рассмотре­ния.

^ Затраты, связанные с приемом и увольнением. Предполагается, что эти затраты являются квадратичной функцией изменения фонда рабочей силы (W_t - W _t-1) — и описываются величиной, которые должны быть определены, причем константа с₁₁ учитывает асимметрию функции затрат.

^ Затраты, связанные со сверхурочными работами и простоями. При условии, что фонд рабочего времени равен W_t. желаемый объем производства определяется величиной c_tW_t. Если объем производства превышает это количество, то будут иметь место затраты, связанные со сверхурочной работой; если же объем производства менее чем величина c₄W_t, то будут иметь место издержки, связанные с простоями. Рассматриваемые затраты характеризуются величиной с₃ (P_t — с₄ W_t)² + c5Pt-c6Wt+C12PtWt, где последние три члена включены для повышения точности.

Затраты, связанные с хранением запасов. Издержки, обуслов­ленные невыполнением заказов. Предполагается, что затраты, связанные с хранением запасов, описываются величиной C7[It — (^C₈ +_C9dt)]², где d_t— ожидаемый уровень спроса на агре­гированный продукт в течение t-го интервала времени.

Планируемый уровень запасов определяется величиной c₈+ C9dt. Отклонения от этого уровня приводят к затратам на хранение запасов или к издержкам, обусловленным невыполне­нием заказов, причем затраты и издержки возрастают пропор­ционально квадрату отклонений.

В работе [39] значение с₉ было принято равным нулю. Расчет коэффициентов затрат является длительной дорогостоящей про­цедурой, требующей статистического анализа данных учета и данных о системе управления.

Рядом исследователей была проделана большая работа с целью улучшения качества оценок составляющих затрат [55] и опреде­ления функций агрегированных затрат, характеризующих за­траты на производство отдельных изделий [54].

^ Построение модели. Задача агрегированного планирования производства с учетом структуры затрат может быть сформулиро­вана как минимизация ожидаемых затрат: найти



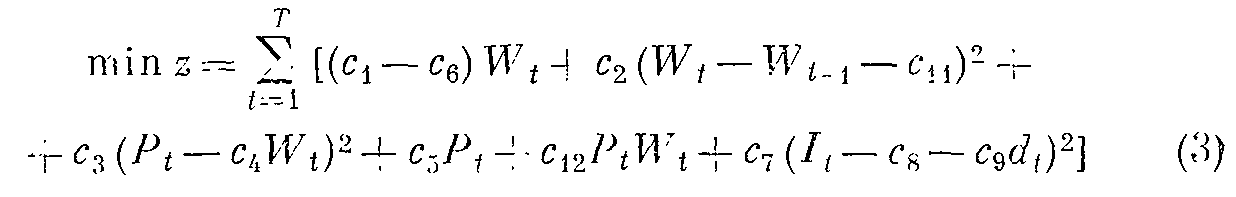
при ограничениях



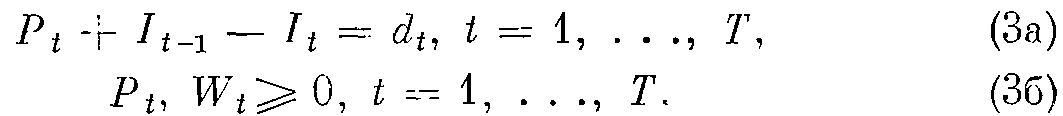
Одним из возможных подходов является отказ от предполо­жения о детерминированности спроса d_t. В работе [56] показано, что при перемещенных оценках прогнозируемого спроса решение сформулированной задачи при ограничениях (За), (36) дает мини­мум ожидаемых затрат.

2.1. Линейные решающие правила.

Если целевая функция рассматриваемой модели строго вы­пуклая, то она имеет единственный глобальный минимум. Это условие обычно выполняется в тех случаях, когда имеет место возрастание предельных затрат.

Оптимальное решение задачи находят с помощью метода мно­жителей Лагранжа.

Несколько примеров решения задач агрегированного плани­рования с помощью конкретных решающих правил описаны в ра­боте [И].

В общем виде линейные решающие правила могут быть пред­ставлены уравнениями вида



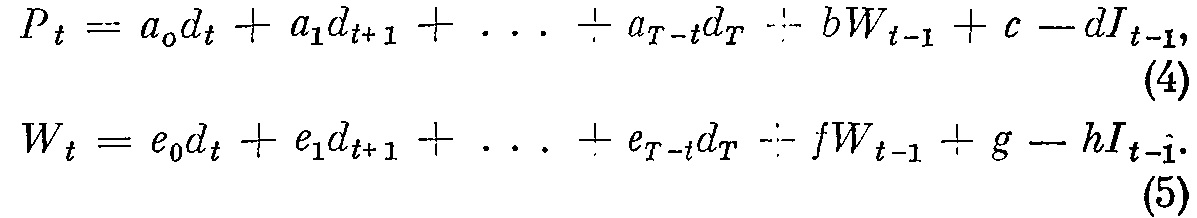
Уравнение (4) устанавливает зависимость объема производи­мой агрегированной продукции в течение t-гo интервала времени от прогнозов будущего спроса, фонда рабочей силы в течение времени (T— 1) и уровня начального запаса.

Агрегированный фонд рабочей силы (5) в течение t-гo интер­вала времени также линейно зависит от прогнозов будущего спро­са, фонда рабочей силы в течение (t — 1)-го интервала времени и уровня начального запаса.

Значения весов множителей (а и е), приписываемых прогнози­руемым опросам, быстро убывают к концу периода планирования.