Вероятность произведения событий. Условная вероятность
| Вид материала | Документы |
- Основные простейшие теоремы теории вероятностей, 32.04kb.
- Программа курса лекций, 26.81kb.
- Лекция Условная вероятность, независимость, 67.33kb.
- Контрольная работа №4. по дисциплине «ТВиМС», 25.55kb.
- Лекция Управление рисками проекта, 216.18kb.
- Курс «Вероятность» является вторым в ряду вероятностно-эконометрических курсов Вероятность, 32.07kb.
- Основные виды случайных величин, 49.77kb.
- Введение, 58.17kb.
- Томский Государственный Университет Систем Управления и Радиоэлектроники (тусур) Томский, 19.19kb.
- Программа обсуждена на заседании кафедры Математики фнти, 75.2kb.
Основные определения ~ Действия со случайными событиями ~ Вероятность события. Аксиоматическое определение вероятности ~ Вероятность события. Классическое определение вероятности ~ Вероятность суммы событий ~ Вероятность произведения событий. Условная вероятность. Независимые события ~ Формула полной вероятности. Формулы Байеса
Основные определения. Будем полагать, что результатом реального опыта (эксперимента) может быть один или несколько взаимоисключающих исходов; эти исходы неразложимы и взаимно исключают друг друга. В этом случае говорят, что эксперимент заканчивается одним и только одним элементарным исходом.
Множество всех элементарных событий, имеющих место в результате случайного эксперимента, будем называть пространством элементарных событий (элементарное событие соответствует элементарному исходу).
^ Случайными событиями (событиями), будем называть подмножества пространства элементарных событий .
Пример 1. Подбросим монету один раз. Монета может упасть цифрой вверх - элементарное событие ц (или 1), или гербом - элементарное событие Г (или 2). Соответствующее пространство элементарных событий состоит из двух элементарных событий:
= { ц, Г } или = { 1, 2}.
Пример 2. Бросаем один раз игральную кость. В этом опыте пространство элементарных событий = { 1, 2, 3, 4, 5, 6}, где i- выпадение i очков. Событие A - выпадение четного числа очков, A = { 2, 4, 6}, A
 .
.Пример 3. На отрезке [0, 1] наугад (случайно) поставлена точка. Измеряется расстояние точки от левого конца отрезка. В этом опыте пространство элементарных событий = [0, 1] - множество действительных чисел на единичном отрезке.
В более точных, формальных терминах элементарные события и пространство элементарных событий описывают следующим образом.
^ Пространством элементарных событий называют произвольное множество , ={}. Элементы этого множества называют элементарными событиями.
Понятия элементарное событие, событие, пространство элементарных событий, являются первоначальными понятиями теории вероятностей. Невозможно привести более конкретное описание пространства элементарных событий. Для описания каждой реальной модели выбирается соответствующее пространство .
Событие называется достоверным событием.
Достоверное событие не может не произойти в результате эксперимента, оно происходит всегда.
Пример 4. Бросаем один раз игральную кость. Достоверное событие состоит в том, что выпало число очков, не меньше единицы и не больше шести, т.е. = { 1, 2, 3, 4, 5, 6}, где i- выпадение i очков, - достоверное событие.
Невозможным событием называется пустое множество
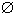 .
. Невозможное событие не может произойти в результате эксперимента, оно не происходит никогда.
^ Случайное событие может произойти или не произойти в результате эксперимента, оно происходит иногда.
Пример 5. Бросаем один раз игральную кость. Выпадение более шести очков - невозможное событие
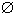 .
. Противоположным событию A называется событие, состоящее в том, что событие A не произошло. Обозначается
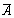 ,
, 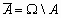 .
.Пример 6. Бросаем один раз игральную кость. Событие A - выпадение четного числа очков, тогда событие
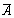 - выпадение нечетного числа очков. Здесь = { 1, 2, 3, 4, 5, 6}, где i- выпадение i очков, A = { 2, 4, 6},
- выпадение нечетного числа очков. Здесь = { 1, 2, 3, 4, 5, 6}, где i- выпадение i очков, A = { 2, 4, 6}, 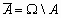 =
= 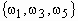 .
.Несовместными событиями называются события A и B, для которых A B =
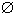 .
.Пример 7. Бросаем один раз игральную кость. Событие A - выпадение четного числа очков, событие ^ B - выпадение числа очков, меньшего двух. Событие AB состоит в выпадении четного числа очков, меньшего двух. Это невозможно, A = { 2, 4, 6}, B = { 1}, AB =
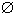 , т.е. события A и B - несовместны.
, т.е. события A и B - несовместны. Действия со случайными событиями
Суммой событий A и B называется событие, состоящее из всех элементарных событий, принадлежащих одному из событий A или B. Обозначается A + B.
Пример 8. Бросаем один раз игральную кость. В этом опыте пространство элементарных событий = { 1, 2, 3, 4, 5, 6}, где элементарное событие i- выпадение i очков. Событие A - выпадение четного числа очков, A = { 2, 4, 6}, событие B - выпадение числа очков, большего четырех, B = { 5, 6}.
Событие A + B = { 2, 4, 5, 6} состоит в том, что выпало либо четное число очков, либо число очков большее четырех, т.е. произошло либо событие A, либо событие B. Очевидно, что A + B
 .
.Произведением событий A и B называется событие, состоящее из всех элементарных событий, принадлежащих одновременно событиям A и B. Обозначается AB.
Пример 9. Бросаем один раз игральную кость. В этом опыте пространство элементарных событий = { 1, 2, 3, 4, 5, 6}, где элементарное событие i- выпадение i очков. Событие A - выпадение четного числа очков, A = { 2, 4, 6}, событие B - выпадение числа очков, большего четырех, B = { 5, 6}.
Событие ^ A B состоит в том, что выпало четное число очков, большее четырех, т.е. произошли оба события, и событие A и событие B, A B = { 6} A B
 .
.Разностью событий A и B называется событие, состоящее из всех элементарных событий принадлежащих A, но не принадлежащих B. Обозначается A\B.
Пример 10. Бросаем один раз игральную кость. Событие A - выпадение четного числа очков, A = { 2, 4, 6}, событие B - выпадение числа очков, большего четырех, B = { 5, 6}. Событие A\ B = { 2, 4} состоит в том, что выпало четное число очков, не превышающее четырех, т.е. произошло событие A и не произошло событие B, A\B
 .
.Очевидно, что
A + A = A, AA = A,
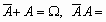
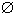 .
. Нетрудно доказать равенства:
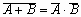 , (A+B)C= AC + BC.
, (A+B)C= AC + BC.Определения суммы и произведения событий переносятся на бесконечные последовательности событий:
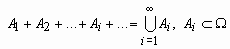 , событие, состоящее из элементарных событий, каждое из которых принадлежит хотя бы одному из
, событие, состоящее из элементарных событий, каждое из которых принадлежит хотя бы одному из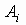 ;
;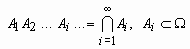 , событие, состоящее из элементарных событий, каждое из которых принадлежит одновременно всем
, событие, состоящее из элементарных событий, каждое из которых принадлежит одновременно всем 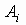 .
.Вероятность события. Аксиоматическое определение вероятности
Пусть - произвольное пространство элементарных событий, а
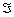 - такая совокупность случайных событий, для которой справедливо:
- такая совокупность случайных событий, для которой справедливо: 
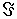 , AB
, AB
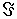 , A+B
, A+B
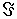 и A\B
и A\B
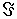 , если A
, если A
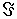 и B
и B
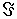 .
.Числовая функция P, определенная на совокупности событий
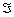 , называется вероятностью, если:
, называется вероятностью, если: - P(A)
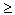 0 для любого A из
0 для любого A из 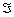 ;
;
- P( ) = 1;
- если A

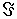 и B
и B
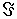 несовместны, то P(A+B) = P(A) + P(B);
несовместны, то P(A+B) = P(A) + P(B);
- для любой убывающей последовательности событий {Ai}из
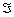 ,
,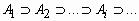 , такой, что
, такой, что 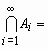
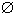 , имеет место равенство
, имеет место равенство 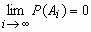 .
.
Тройку
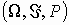 называют вероятностным пространством.
называют вероятностным пространством. Вероятность события. Классическое определение вероятности
Пусть = { 1, 2, …, s} - произвольное конечное пространство элементарных событий, A - событие, состоящее из k элементарных событий: A={ i1, i2, …, ik}, 1
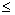 i1
i1 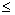 i2
i2 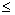 …
… 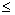 i k
i k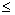 s, k = 1, 2,…, s, и пусть
s, k = 1, 2,…, s, и пусть 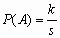 . Определенная таким образом функция P(A) удовлетворяет всем аксиомам 1-4(здесь множество
. Определенная таким образом функция P(A) удовлетворяет всем аксиомам 1-4(здесь множество 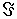 состоит из всех подмножеств множества :
состоит из всех подмножеств множества : 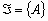 ). Таково классическое определение вероятности события ^ A.
). Таково классическое определение вероятности события ^ A. Принята следующая формулировка классического определения вероятности: вероятностью события A называется отношение числа исходов, благоприятствующих A, к общему числу исходов.
Из приведенных определений следует: P(
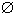 )=0,
)=0, 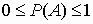 ,
, 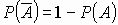 .
.Вероятность суммы событий
Для любых двух событий A и B справедливо:
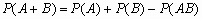 .
.Если события A и B несовместны, то
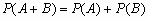 .
. Вероятность произведения событий. Условная вероятность. Независимые события
^ Условная вероятность P(A/B) события A при условии, что событие B произошло, P(B) > 0, определяется формулой
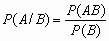 .
.Для любых двух событий A и B справедливо:
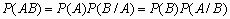 .
.События A и B называются независимыми, если
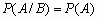 . Для любых двух независимых, событий A и B справедливо:
. Для любых двух независимых, событий A и B справедливо: 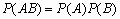 .
.Формула полной вероятности. Формулы Байеса
Пусть ^ A - произвольное событие, а события B1, B2, …, Bn - попарно несовместны и образуют полную группу событий, т.е.
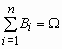 . Тогда имеет место следующая формула для вероятности события A - формула полной вероятности -
. Тогда имеет место следующая формула для вероятности события A - формула полной вероятности - 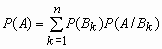 , где P(Bk)>0, k=1, 2, …, n, A
, где P(Bk)>0, k=1, 2, …, n, A  B1+ B2 + …+ Bn.
B1+ B2 + …+ Bn.Если событие A произошло, то вероятность того, что имело место событие Bk
вычисляется по формуле Байеса:
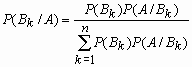 .
.^ Основные определения ~ Функция распределения случайной величины. Её свойства ~ Функция распределения дискретной случайной величины ~ Функция распределения и плотность вероятности непрерывной случайной величины ~ Квантили ~ Вероятность попадания в интервал
Основные определения. Результат любого случайного эксперимента можно характеризовать качественно и количественно. Качественный результат случайного эксперимента - случайное событие. Любая количественная характеристика, которая в результате случайного эксперимента может принять одно из некоторого множества значений, - случайная величина. Случайная величина является одним из центральных понятий теории вероятностей.
Пусть
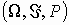 - произвольное вероятностное пространство. Случайной величиной называется действительная числовая функция = ( ),
- произвольное вероятностное пространство. Случайной величиной называется действительная числовая функция = ( ),  , такая, что при любом действительном x
, такая, что при любом действительном x 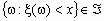 .
.Событие
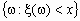 принято записывать в виде < x. В дальнейшем случайные величины будем обозначать строчными греческими буквами , , , …
принято записывать в виде < x. В дальнейшем случайные величины будем обозначать строчными греческими буквами , , , … Случайной величиной является число очков, выпавших при бросании игральной кости, или рост случайно выбранного из учебной группы студента. В первом случае мы имеем дело с дискретной случайной величиной (она принимает значения из дискретного числового множества M={1, 2, 3, 4, 5, 6} ; во втором случае - с непрерывной случайной величиной (она принимает значения из непрерывного числового множества - из промежутка числовой прямой I=[100, 3000]).
^ Функция распределения случайной величины. Её свойства
Каждая случайная величина полностью определяется своей функцией распределения.
Если .- случайная величина, то функция F(x) = F (x) = P( < x) называется функцией распределения случайной величины . Здесь P( < x) - вероятность того, что случайная величина принимает значение, меньшее x.
Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением.
Функция распределения любой случайной величины обладает следующими свойствами:
- F(x) определена на всей числовой прямой R;
- F(x) не убывает, т.е. если x1
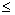 x2, то F(x1)
x2, то F(x1)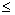 F(x2);
F(x2);
- F(-
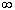 )=0, F(+
)=0, F(+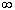 )=1, т.е.
)=1, т.е. 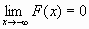 и
и 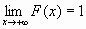 ;
;
- F(x) непрерывна справа, т.е.
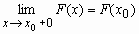
.
Функция распределения дискретной случайной величины
Если - дискретная случайная величина, принимающая значения x1 < x2 < … < xi < … с вероятностями p1 < p2 < … < pi < …, то таблица вида
| x1 | x2 | … | xi | … |
| p1 | p2 | … | pi | … |
называется распределением дискретной случайной величины.
Функция распределения случайной величины, с таким распределением, имеет вид
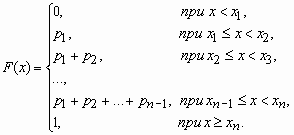
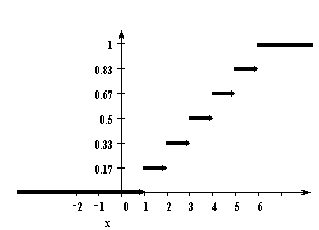
У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |