Вероятность произведения событий. Условная вероятность
| Вид материала | Документы |
СодержаниеРаспределение Стьюдента Логистическое распределение Логнормальное распределение Распределение Вейбулла Распределение Коши Теорема Пуассона Теорема Бернулли Независимость случайных величин |
- Основные простейшие теоремы теории вероятностей, 32.04kb.
- Программа курса лекций, 26.81kb.
- Лекция Условная вероятность, независимость, 67.33kb.
- Контрольная работа №4. по дисциплине «ТВиМС», 25.55kb.
- Лекция Управление рисками проекта, 216.18kb.
- Курс «Вероятность» является вторым в ряду вероятностно-эконометрических курсов Вероятность, 32.07kb.
- Основные виды случайных величин, 49.77kb.
- Введение, 58.17kb.
- Томский Государственный Университет Систем Управления и Радиоэлектроники (тусур) Томский, 19.19kb.
- Программа обсуждена на заседании кафедры Математики фнти, 75.2kb.
Распределение хи-квадрат ( 2- распределение)
Пусть 1, 2, …, n - независимые случайные величины, каждая из которых имеет стандартное нормальное распределение N(0, 1). Составим случайную величину
2 = 12 + 22 + …+ n2.
Ее закон распределения называется 2- распределением с nстепенями свободы. Плотность вероятности этой случайной величины вычисляется по формуле:
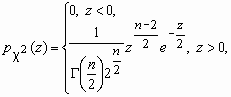
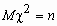 , D 2=2n.
, D 2=2n. Здесь
 - гамма-функция Эйлера.
- гамма-функция Эйлера.^ Распределение Стьюдента
Пусть случайная величина имеет стандартное нормальное распределение, а случайная величина n2 - 2-распределение с n степенями свободы. Если и n2 - независимы, то про случайную величину
 говорят, что она имеет распределение Стьюдента с nстепенями свободы. Плотность вероятности этой случайной величины вычисляется по формуле:
говорят, что она имеет распределение Стьюдента с nстепенями свободы. Плотность вероятности этой случайной величины вычисляется по формуле: 
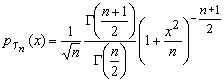 , x
, x R, M n = 0, D n = n/(n-2), n>2.
R, M n = 0, D n = n/(n-2), n>2.При больших n распределение Стьюдента практически не отличается от N(0, 1).
F-распределение Фишера
Пусть случайные величины n2и m2 независимы и имеют распределение 2 с n и mстепенями свободы соответственно. Тогда о случайной величине
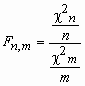 говорят, что она имеет F-распределение. Плотность вероятности этой случайной величины вычисляется по формуле:
говорят, что она имеет F-распределение. Плотность вероятности этой случайной величины вычисляется по формуле:  , x>0,
, x>0,  - гамма-функция Эйлера;
- гамма-функция Эйлера; 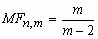 , m>2;
, m>2; 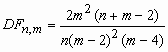 , m > 4.
, m > 4.Распределение Парето
Распределение Парето часто применяется в экономических исследованиях. Плотность вероятностей для случайной величины, распределенной по Парето, имеет вид

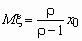 ,
, 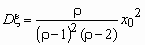 .
.Распределение Парето имеет математическое ожидание только при > 1, а дисперсию - только при > 2. Cлучайная величина, распределенная по Парето, принимает значения только в области x
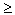 x0, x0 > 0.
x0, x0 > 0.^ Логистическое распределение
Это еще одно распределение, широко применяемое в экономических исследованиях. Для случайной величины , имеющей логистическое распределение, функция распределения и функция плотности вероятностей имеют соответственно вид:
 ,
,  ,
,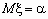 ,
, 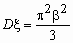 , x
, x  R, и - параметры распределения.
R, и - параметры распределения. По своим свойствам логистическое распределение очень похоже на нормальное.
^ Логнормальное распределение
Случайная величина имеет логарифмическое нормальное (логнормальное) распределение с параметрами a и , если случайная величина ln имеет нормальное распределение с параметрами a >и . Функция распределения и функция плотности вероятностей логнормального распределения имеют соответственно вид:
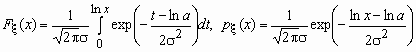 ,
,  ,
, 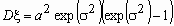 .
. Бета-распределение
Случайная величина имеет В-распределение (бета-распределение) с параметрами a1 и a2, если ее функция плотности вероятностей имеет вид:
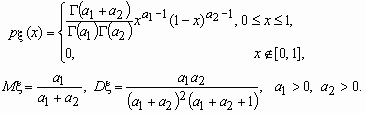
^ Распределение Вейбулла
Случайная величина имеет распределение Вейбулла с параметрами 0 и , если ее функция распределения и функция плотности вероятностей имеют соответственно вид:
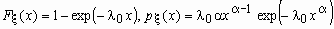 ,
, 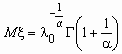 ,
,  ,
,  - гамма-функция Эйлера.
- гамма-функция Эйлера.^ Распределение Коши
Случайная величина имеет распределение Коши с параметрами a и c, если ее функция распределения и функция плотности вероятностей имеют соответственно вид:

У распределения Коши не существует ни математического ожидания, ни дисперсии. Это распределение не имеет ни одного момента положительного порядка.
Гамма-распределение
Случайная величина имеет Г-распределение (гамма-распределение) с параметрами a и b, если ее функция плотности вероятностей имеет вид:
 , a > 0, b > 0,
, a > 0, b > 0,  ,
,  ,
,  .
. Распределение Лапласа
Случайная величина имеет распределение Лапласа (двустороннее экспоненциальное распределение) с параметром , если ее функция плотности вероятностей имеет вид:
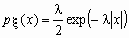 , -
, -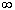 < x <
< x < 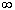 , M = 0, D = 2/ 2.
, M = 0, D = 2/ 2.Теорема Пуассона ~ Локальная теорема Муавра—Лапласа ~ Интегральная теорема Муавра—Лапласа ~ Теорема Бернулли
Если число испытаний n в схеме независимых испытаний Бернулли растет, а вероятность p уменьшается, то точная формула
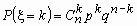 практически непригодна из-за громоздких вычислений и возникающих погрешностей округления. В этом случае пользуются приближенными формулами Пуассона (при npq < 9) и Муавра-Лапласа (npq > 9).
практически непригодна из-за громоздких вычислений и возникающих погрешностей округления. В этом случае пользуются приближенными формулами Пуассона (при npq < 9) и Муавра-Лапласа (npq > 9).^ Теорема Пуассона
Если число испытаний n в схеме независимых испытаний Бернулли стремится к бесконечности и
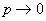 так, что
так, что 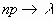 ,
, 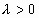 , то при любых
, то при любых 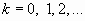
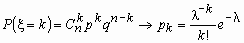
Это означает, что при больших n и малых p вместо громоздких вычислений по точной формуле
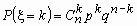 можно воспользоваться приближенной формулой
можно воспользоваться приближенной формулой 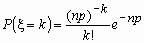 , т.е. использовать формулу Пуассона для = np.
, т.е. использовать формулу Пуассона для = np.На практике пуассоновским приближением пользуются при npq < 9.
Локальная теорема Муавра-Лапласа
Пусть 0< p <1 и величина
 при n
при n 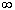 ограничена. Тогда
ограничена. Тогда 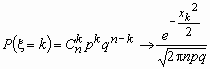 .
. На практике приближением Муавра-Лапласа пользуются при npq > 9.
Точность формулы
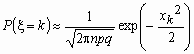 растет, как с ростом величин n и k, так и по мере приближения величин p и q к 0.5.
растет, как с ростом величин n и k, так и по мере приближения величин p и q к 0.5.Интегральная теорема Муавра-Лапласа
Пусть 0< p <1, тогда для схемы Бернулли при n
 для любых a и b справедлива формула
для любых a и b справедлива формула .
.Отсюда, в частности, следует, что для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k1 и k2, можно использовать формулу
 ,
,где
 ,
,  ,
, 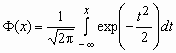 - функция Лапласа.
- функция Лапласа. Точность этой приближенной формулы растет с ростом n.
Если npq сравнительно невелико, то лучшее приближение дает формула
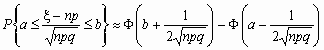
и для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k1 и k2, можно использовать формулу
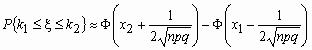 , где
, где 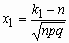 ,
,  .
.^ Теорема Бернулли
Если - число успехов в n испытаниях Бернулли с вероятностью успеха в одном испытании p, 0 < p < 1, то для любого > 0 справедливо:
 .
.Утверждение теоремы Бернулли означает, что с ростом числа испытаний n относительная частота успехов /n приближается к вероятности p успеха в одном испытании.
Достаточно часто возникает необходимость установить, сколько нужно произвести испытаний, чтобы отклонение относительной частоты успехов /n от вероятности p с вероятностью, больше или равной
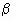 было меньше
было меньше  . Т.е. требуется найти n, для которого справедливо неравенство
. Т.е. требуется найти n, для которого справедливо неравенство 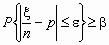 . Доказано, что число n, которое обеспечивает выполнение этого неравенства, удовлетворяет соотношению
. Доказано, что число n, которое обеспечивает выполнение этого неравенства, удовлетворяет соотношению  , где
, где 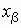 - решение уравнения
- решение уравнения 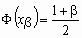 . Следует обратить особое внимание на замечательный факт: искомое значение n не зависит от p!
. Следует обратить особое внимание на замечательный факт: искомое значение n не зависит от p!Многомерные случайные величины. Функции распределения многомерных случайных величин ~ ^ Независимость случайных величин ~ Условные распределения случайных величин ~ Условные распределения дискретных случайных величин ~ Условные распределения непрерывных случайных величин
В одном и том же случайном эксперименте можно рассматривать не одну, а несколько - n - числовых функций, определенных на одном и том же пространстве элементарных событий. Совокупность таких функций называется многомерной случайной величиной или случайным вектором и обозначается
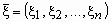 .
.Точнее. На вероятностном пространстве
 заданы случайные величины
заданы случайные величины  ; каждому
; каждому  эти величины ставят в соответствие n-мерный вектор
эти величины ставят в соответствие n-мерный вектор 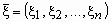 , который называется n-мерным случайным вектором (n-мерной случайной величиной).
, который называется n-мерным случайным вектором (n-мерной случайной величиной).Многомерные случайные величины. Функции распределения многомерных случайных величин.
Функцией распределения случайного вектора
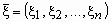 или совместным распределением случайных величин
или совместным распределением случайных величин 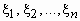 называется функция, определенная равенством
называется функция, определенная равенством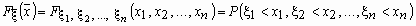 ,
, где
 .
.По известной многомерной функции
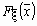 можно найти распределение каждой из компонент
можно найти распределение каждой из компонент 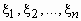 .
. Например, если
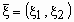 - двумерная случайная величина, имеющая совместное распределение
- двумерная случайная величина, имеющая совместное распределение  , то распределения компонент
, то распределения компонент  и
и  вычисляются соответственно по формулам:
вычисляются соответственно по формулам:  ,
, 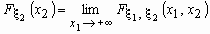 .
.В дальнейшем будем рассматривать двумерные случайные векторы.
Случайный вектор
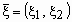 называется непрерывным случайным вектором, если существует такая неотрицательная функция
называется непрерывным случайным вектором, если существует такая неотрицательная функция 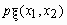 , что для любого прямоугольника на плоскости
, что для любого прямоугольника на плоскости 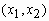 вероятность события
вероятность события  равна
равна 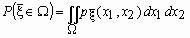 .
.Функция
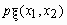 в этом случае называется совместной плотностью распределения.
в этом случае называется совместной плотностью распределения.Легко показать, что
 .
.Если
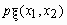 - совместная плотность распределения двумерного случайного вектора
- совместная плотность распределения двумерного случайного вектора 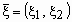 , то плотности распределения его компонент определяются равенствами:
, то плотности распределения его компонент определяются равенствами: и
и 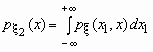 .
.Если
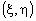 - дискретный случайный вектор, то совместным распределением случайных величин
- дискретный случайный вектор, то совместным распределением случайных величин  и
и  чаще всего называют таблицу вида
чаще всего называют таблицу вида| | y1 | y2 | ... | ym |
| x1 | p11 | p12 | ... | p1m |
| x2 | p12 | p12 | ... | p2m |
| ... | ... | ... | pij | ... |
| xn | pn1 | pn2 | ... | pnm |
где
 и
и 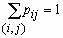 .
.По этой таблице можно найти распределения
 и
и 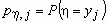 компонент и . Они вычисляются по формулам:
компонент и . Они вычисляются по формулам: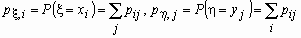 .
.Независимость случайных величин
Решить обратную задачу, т.е. восстановить совместное распределение ( , ) по распределениям величин и , вообще говоря, невозможно. Однако эту задачу можно решить, когда случайные величины и независимы.
Случайные величины и называются независимыми, если для любых x1, x2
 R2 справедливо равенство:
R2 справедливо равенство:F , (x1, x2)= Fx (x1)Fh ( x2).
Для непрерывных случайных величин это определение эквивалентно следующему:
случайные величины называются независимыми, если
p , (x1, x2)= p (x1) p (x2)
во всех точках непрерывности входящих в это равенство функций.
Для дискретных случайных величин и с матрицей совместного распределения {pij} условие независимости и имеет вид:
pij = P( = xi, = yj) = P( = xi) P( = yj),
для всех i = 1, 2, …, n, j = 1, 2, …, m.
