Вероятность произведения событий. Условная вероятность

Вид материала

Документы

Содержание Функция распределения и плотность вероятности непрерывной случайной величины Дисперсия случайной величины Математическое ожидание случайной величины Математическое ожидание непрерывной случайной величины Начальным моментом k-го порядка Средним гармоническим Средним геометрическим Биномиальное распределение Гипергеометрическое распределение Пуассоновское распределение Экспоненциальное (показательное) распределение Нормальное распределение

Подобный материал:

• Основные простейшие теоремы теории вероятностей, 32.04kb.
• Программа курса лекций, 26.81kb.
• Лекция Условная вероятность, независимость, 67.33kb.
• Контрольная работа №4. по дисциплине «ТВиМС», 25.55kb.
• Лекция Управление рисками проекта, 216.18kb.
• Курс «Вероятность» является вторым в ряду вероятностно-эконометрических курсов Вероятность, 32.07kb.
• Основные виды случайных величин, 49.77kb.
• Введение, 58.17kb.
• Томский Государственный Университет Систем Управления и Радиоэлектроники (тусур) Томский, 19.19kb.
• Программа обсуждена на заседании кафедры Математики фнти, 75.2kb.

^ Функция распределения и плотность вероятности непрерывной случайной величины

Если функция распределения F_ (x) непрерывна, то случайная величина  называется непрерывной случайной величиной.

Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины p_ (x), которая связана с функцией распределения F_ (x) формулам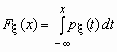и

и .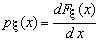

Отсюда, в частности, следует, что для любой случайной величины .

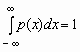Квантили

При решении практических задач часто требуется найти значение x, при котором функция распределения F_ (x) случайной величины  принимает заданное значение p, т.е. требуется решить уравнение F_ (x) = p. Решения такого уравнения (соответствующие значения x) в теории вероятностей называются квантилями.

Квантилью x_p (p-квантилью, квантилью уровня p) случайной величины , имеющей функцию распределения F_ (x), называют решение x_p уравнения F_ (x) = p, p (0, 1). Для некоторых p уравнение F_ (x) = p может иметь несколько решений, для некоторых - ни одного. Это означает, что для соответствующей случайной величины некоторые квантили определены неоднозначно, а некоторые кванитили не существуют.

Квантили, наиболее часто встречающиеся в практических задачах, имеют свои названия:

медиана - квантиль уровня 0.5;

нижняя квартиль - квантиль уровня 0.25;

верхняя квартиль - квантиль уровня 0.75;

децили - квантили уровней 0.1, 0.2, …, 0.9;

процентили - квантили уровней 0.01, 0.02, …, 0.99.

Вероятность попадания в интервал

Вероятность того, что значение случайной величины F_ (x) попадает в интервал (a, b), равная P(a <  < b) = F_ (b) -F_ (a), вычисляется по формулам:

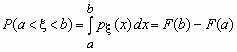- для непрерывной случайной величины и

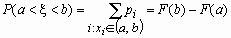- для дискретной случайной величины.

Если a= - 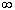, то ,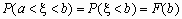

если b= 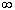, то .


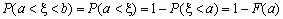Математическое ожидание случайной величины ~ ^ Дисперсия случайной величины ~ Моменты ~ Ассиметрия ~ Эксцесс ~ Среднее геометрическое и среднее гармоническое

 

Каждая случайная величина полностью определяется своей функцией распределения.

В то же время при решении практических задач достаточно знать несколько числовых параметров, которые позволяют представить основные особенности случайной величины в сжатой форме. К таким величинам относятся в первую очередь математическое ожидание и дисперсия.

 

^ Математическое ожидание случайной величины

Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины  обозначается M .

Математическое ожидание дискретной случайной величины  , имеющей распределение

 

x1	x2	...	xn
p1	p2	...	pn

называется величина 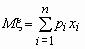, если число значений случайной величины конечно.

Если число значений случайной величины счетно, то 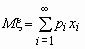. При этом, если ряд в правой части равенства расходится, то говорят, что случайная величина  не имеет математического ожидания.

^ Математическое ожидание непрерывной случайной величины с плотностью вероятностей p_ (x) вычисляется по формуле . При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина  не имеет математического ожидания.

Если случайная величина  является функцией случайной величины  ,  = f(x), то

.

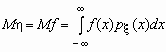Аналогичные формулы справедливы для функций дискретной случайной величины:

, .

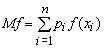Основные свойства математического ожидания:

• математическое ожидание константы равно этой константе, Mc=c ;
  

• математическое ожидание - линейный функционал на пространстве случайных величин, т.е. для любых двух случайных величин  ,  и произвольных постоянных a и b справедливо: M(a + b ) = a M( )+ b M( );
  

• математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(  ) = M( )M( ).
  

 

Дисперсия случайной величины

Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.

Если случайная величина  имеет математическое ожидание M , то дисперсией случайной величины  называется величина D = M( - M )².

Легко показать, что D = M( - M )²= M ² - M( )².

Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина M ² >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам

, .

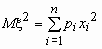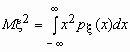Для определения меры разброса значений случайной величины часто используется среднеквадратичное отклонение 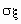, связанное с дисперсией соотношением .

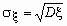Основные свойства дисперсии:

• дисперсия любой случайной величины неотрицательна, D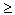 0;
  

• дисперсия константы равна нулю, Dc=0;
  

• для произвольной константы D(c ) = c²D( );
  

• дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(   ) = D( ) + D ( ).
  

Моменты

В теории вероятностей и математической статистике, помимо математического ожидания и дисперсии, используются и другие числовые характеристики случайных величин. В первую очередь это начальные и центральные моменты.

^ Начальным моментом k-го порядка случайной величины  называется математическое ожидание k-й степени случайной величины  , т.е.  _k = M ^k.

Центральным моментом k-го порядка случайной величины  называется величина  _k, определяемая формулой  _k = M( - M )^k.

Заметим, что математическое ожидание случайной величины - начальный момент первого порядка,  ₁ = M , а дисперсия - центральный момент второго порядка,

 ₂ = M ² = M( - M )² = D .

Существуют формулы, позволяющие выразить центральные моменты случайной величины через ее начальные моменты, например:

 ₂= ₂- ₁²,  ₃ =  ₃ - 3 _{2 1} + 2 ₁³.

Если плотность распределения вероятностей непрерывной случайной величины симметрична относительно прямой x = M , то все ее центральные моменты нечетного порядка равны нулю.


Асимметрия

В теории вероятностей и в математической статистике в качестве меры асимметрии распределения является коэффициент асимметрии, который определяется формулой ,

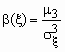где  ₃ - центральный момент третьего порядка, - среднеквадратичное отклонение.


Эксцесс

Нормальное распределение наиболее часто используется в теории вероятностей и в математической статистике, поэтому график плотности вероятностей нормального распределения стал своего рода эталоном, с которым сравнивают другие распределения. Одним из параметров, определяющих отличие распределения случайной величины  , от нормального распределения, является эксцесс.

Эксцесс  случайной величины  определяется равенством .

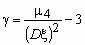У нормального распределения, естественно,  = 0. Если  ( ) > 0, то это означает, что график плотности вероятностей p_ (x) сильнее “заострен”, чем у нормального распределения, если же  ( ) < 0, то “заостренность” графика p_ (x) меньше, чем у нормального распределения.


Среднее геометрическое и среднее гармоническое

Среднее гармоническое и среднее геометрическое случайной величины - числовые характеристики, используемые в экономических вычислениях.

^ Средним гармоническим случайной величины, принимающей положительные значения, называется величина .

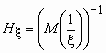Например, для непрерывной случайной величины, распределенной равномерно на [a, b],

0 < a < b, среднее гармоническое вычисляется следующим образом:

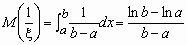и .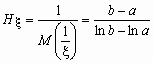

^ Средним геометрическим случайной величины, принимающей положительные значения, называется величина .

Название “среднее геометрическое” происходит от выражения среднего геометрического дискретной случайной величины, имеющей равномерное распределение

 

	a1	a2	a3	...	an
p	1/n	1/n	1/n	...	1/n

 

Среднее геометрическое, вычисляется следующим образом:

,

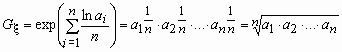т.е. получилось традиционное определение среднего геометрического чисел a₁, a₂, …, a_n.

Например, среднее геометрическое случайной величины, имеющей показательное распределение с параметром  , вычисляется следующим образом:

, .

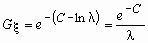Здесь С  0.577 - постоянная Эйлера.


^ Биномиальное распределение ~ Геометрическое распределение ~ Гипергеометрическое распределение ~ Пуассоновское распределение

 

Биномиальное распределение

Пусть проводится серия из n независимых испытаний, каждое из которых заканчивается либо “успехом” либо “неуспехом”. Пусть в каждом испытании (опыте) вероятность успеха p, а вероятность неуспеха q = 1- p. С таким испытанием можно связать случайную величину  , значение которой равно числу успехов в серии из n испытаний. Эта величина принимает значения от 0 до n. Ее распределение называется биномиальным и определяется формулой Бернулли

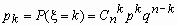, 0 < p <1, k = 0, 1, …, n, 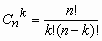, M = np, D = npq, .

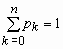Геометрическое распределение

Со схемой испытаний Бернулли можно связать еще одну случайную величину  - число испытаний до первого успеха. Эта величина принимает бесконечное множество значений от 0 до + 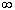и ее распределение определяется формулой

p_k = P(= k) = q^k-1 p, 0 <p <1, k=1, 2, … , , , .

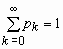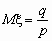^ Гипергеометрическое распределение

В партии из N изделий имеется M (M < N) доброкачественных и N - M дефектных изделий. Если случайным образом из всей партии выбрать контрольную партию из n изделий, то число доброкачественных изделий в контрольной партии - случайная величина, которую обозначим. Распределение такой случайной величины называется гипергеометрическим и имеет вид:

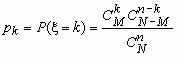, k = 0, 1, …, min(n,M), ,

, .

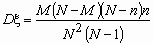^ Пуассоновское распределение

Пуассоновское распределение c параметром  имеет случайная величина  , принимающая целые неотрицательные значения k = 0, 1, 2, … с вероятностями p_k:

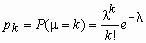, , M =, D =  ,  > 0 - параметр распределения.


Равномерное распределение ~ Экспоненциальное (показательное) распределение ~ Нормальное распределение ~ Распределение хи-квадрат (c ²- распределение) ~ F-распределение Фишера ~ Распределение Парето ~ Логистическое распределение ~ Логнормальное распределение ~ Вета-распределение ~ Распределение Вейбулла ~ Распределение Коши ~ Гамма-распределение ~ Распределение Лапласа

 

Равномерное распределение

Непрерывная случайная величина  , принимающая значения на отрезке [a, b], распределена равномерно на [a, b], если ее плотность распределения p_ (x) и функция распределения F_x (x ) имеют соответственно вид:

, .

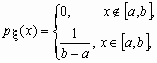
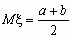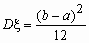^ Экспоненциальное (показательное) распределение

Непрерывная случайная величина  имеет показательное распределение с параметром  > 0, если она принимает только неотрицательные значения, а ее плотность распределения p_ (x )и функция распределения F_ (x) имеют соответственно вид:

, .

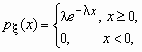
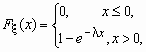
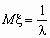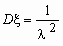^ Нормальное распределение

Нормальное распределение играет исключительно важную роль в теории вероятностей и математической статистике.

Случайная величина  нормально распределена с параметрами a и  ,  >0, если ее плотность распределения p_ (x ) и функция распределения F_ (x) имеют соответственно вид:

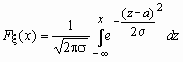, , M = a, D =  ²_.

Часто используемая запись  ~ N(a,  ) означает, что случайная величина  имеет нормальное распределение с параметрами a и  .

Говорят, что случайная величина  имеет стандартное нормальное распределение, если a = 0 и  = 1 ( ~ N(0, 1)). Плотность и функция распределения стандартного нормального распределения имеют вид:

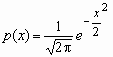, , M = 0, D = 1.

Здесь 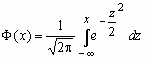- функция Лапласа.

Функция распределения нормальной величины  ~ N(a,  ) выражается через функцию Лапласа следующим образом: .

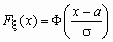Если  ~ N(a,  ), то случайную величину  = (x-a)/ называют стандартизованной или нормированной случайной величиной;  ~ N(0, 1) - имеет стандартное нормальное распределение.