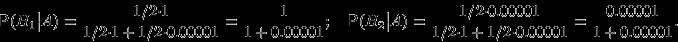Лекция Условная вероятность, независимость
| Вид материала | Лекция |
СодержаниеПример 17 (пример 4.3. Формула полной вероятности Теорема 8 (формула полной вероятности). 4.4. Формула Байеса |
- Программа курса лекций, 26.81kb.
- Вероятность произведения событий. Условная вероятность, 395.39kb.
- Лекция Управление рисками проекта, 216.18kb.
- Программа обсуждена на заседании кафедры Математики фнти, 75.2kb.
- Д. Б. Гнеденко 1/2 года, 3 курс, экономический поток Лекция, 21.85kb.
- Контрольная работа №4. по дисциплине «ТВиМС», 25.55kb.
- Курс «Вероятность» является вторым в ряду вероятностно-эконометрических курсов Вероятность, 32.07kb.
- Основные простейшие теоремы теории вероятностей, 32.04kb.
- Основные виды случайных величин, 49.77kb.
- Введение, 58.17kb.
Лекция 4. Условная вероятность, независимость
- Условная вероятность
- Независимость
- Формула полной вероятности
- Формула Байеса

4.1. Условная вероятность
Пример 15.
Кубик подбрасывается один раз. Известно, что выпало более трех очков. Какова при этом вероятность того, что выпало четное число очков?
В данном случае пространство элементарных исходов состоит из трех равновозможных элементарных исходов:
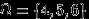 , и событию
, и событию 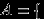 выпало четное число очков
выпало четное число очков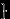 благоприятствуют 2 из них:
благоприятствуют 2 из них: 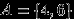 . Поэтому
. Поэтому 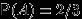 .
. Посмотрим на этот вопрос с точки зрения первоначального эксперимента. Пространство элементарных исходов при одном подбрасывании кубика состоит из шести точек:
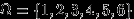 . Слова «известно, что выпало более трех очков» означают, что в эксперименте произошло событие
. Слова «известно, что выпало более трех очков» означают, что в эксперименте произошло событие 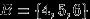 . Слова «какова при этом вероятность того, что выпало четное число очков?» означают, что нас интересует, в какой доле случаев при осуществлении
. Слова «какова при этом вероятность того, что выпало четное число очков?» означают, что нас интересует, в какой доле случаев при осуществлении 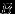 происходит и
происходит и 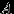 . Вероятность события
. Вероятность события 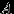 , вычисленную в предположении, что нечто о результате эксперимента уже известно (событие
, вычисленную в предположении, что нечто о результате эксперимента уже известно (событие 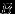 произошло), мы будем обозначать через
произошло), мы будем обозначать через 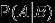 .
.  | Мы хотим вычислить отношение числа исходов, благоприятствующих 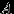 внутри внутри 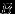 (то есть благоприятствующих одновременно (то есть благоприятствующих одновременно 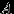 и и 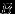 ), к числу исходов, благоприятствующих ), к числу исходов, благоприятствующих 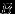 . . 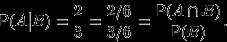 |
Какое отношение требуется вычислить, если элементарные исходы не являются равновозможными?
Определение 15.
Условной вероятностью события
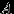 при условии, что произошло событие
при условии, что произошло событие 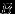 , называется число
, называется число 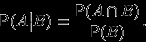
Будем считать, что условная вероятность определена только в случае, когда
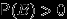 .
. Следующее свойство называется "теоремой умножения":
Теорема 6.
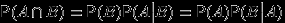 ,
, если соответствующие условные вероятности определены (то есть если
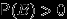 ,
, 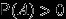 ).
). Теорема умножения для большего числа событий:
Теорема 7.
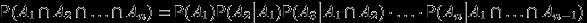 ,
, если соответствующие условные вероятности определены.
Доказать теорему 7 методом математической индукции.

4.2. Независимость
Определение 16.
События
 и
и 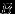 называются независимыми, если
называются независимыми, если 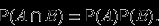
Пример 16.
1. Точка с координатами
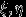 бросается наудачу в квадрат со стороной 1.
бросается наудачу в квадрат со стороной 1. Доказать, что для любых
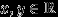 события
события 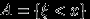 и
и 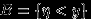 независимы.
независимы.2. Точка с координатами
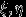 бросается наудачу в треугольник с вершинами (1,0), (0,0) и (0,1).
бросается наудачу в треугольник с вершинами (1,0), (0,0) и (0,1). Доказать, что события
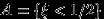 и
и 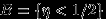 зависимы.
зависимы.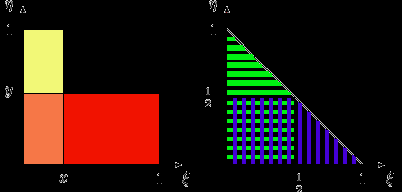
1. Рассмотрим
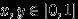 (разобрать остальные случаи). Видим, что
(разобрать остальные случаи). Видим, что 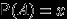 ,
, 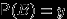 ,
, 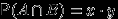 , так что события
, так что события 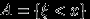 и
и 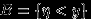 независимы.
независимы.2. На рисунке событие
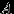 заштриховано зеленым, событие
заштриховано зеленым, событие 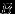 — синим. Видим, что
— синим. Видим, что 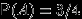 ,
, 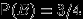 ,
, 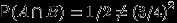 ,
, так что события
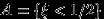 и
и 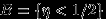 зависимы.
зависимы. Доказать, что при
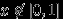 или
или 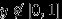 события
события 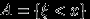 и
и 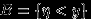 независимы.
независимы. Замечание 7.
Если события
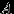 и
и 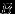 несовместны, то они независимы если и только если
несовместны, то они независимы если и только если 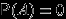 или
или 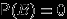 .
.Доказать!!
Следствие 2.
Если
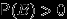 , то события
, то события 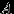 и
и 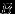 независимы
независимы 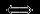
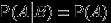 .
. Если
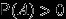 , то события
, то события 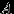 и
и 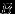 независимы
независимы 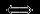
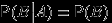 .
. Доказать следствие, пользуясь определением условной вероятности.
Лемма 2.
Если события
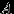 и
и 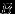 независимы, то независимы и события
независимы, то независимы и события 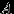 и
и 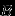 ,
, 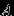 и
и 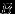 ,
, 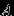 и
и 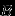 .
. Доказательство.
Так как
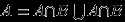 , и события
, и события 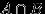 и
и 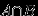 несовместны, то
несовместны, то 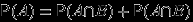 .Поэтому
.Поэтому 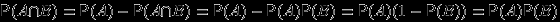 .
. Вывести отсюда все остальные утверждения.
Q.D.E.
Определение 17.
События
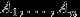 называются независимыми в совокупности, если для любого набора
называются независимыми в совокупности, если для любого набора 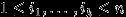
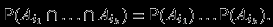 | (6) |
Упражнение.
Сколько равенств должно выполняться одновременно в условии (6)? А вы посчитали общее число подмножеств множества из n элементов?
Перечислите, какие равенства должны иметь место, чтобы четыре события A,B,C,D были независимы в совокупности.
Замечание 8.
Если события
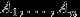 независимы в совокупности, то они попарно независимы, то есть любые два события
независимы в совокупности, то они попарно независимы, то есть любые два события 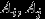 независимы. Достаточно в равенстве (6) взять
независимы. Достаточно в равенстве (6) взять 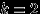 . Обратное, как показывает следующий пример, неверно.
. Обратное, как показывает следующий пример, неверно. Пример 17 (пример С.Н.Бернштейна).
Рассмотрим правильный тетраэдр, 3 грани которого окрашены, соответственно, в красный, синий, зеленый цвета, а четвертая грань содержит все три цвета. Событие
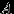 (
(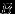 ,
, 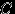 ) означает, что выпала грань, содержащая красный (синий, зеленый) цвета.
) означает, что выпала грань, содержащая красный (синий, зеленый) цвета. Вероятность каждого из этих событий равна 1/2, так как каждый цвет есть на двух гранях из четырех. Вероятность пересечения любых двух из них равна 1/4, так как только одна грань содержит два цвета. А так как
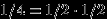 , то все события попарно независимы.
, то все события попарно независимы. Но вероятность пересечения всех трех тоже равна 1/4, а не 1/8, то есть события не являются независимыми в совокупности.
Заметьте, что равенство (6) выполнено для
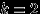 , но не выполнено для
, но не выполнено для 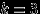 .
. 
4.3. Формула полной вероятности
Пример 18.
Есть 3 завода, производящих одну и ту же продукцию. При этом 1-й завод производит 25%, 2-й завод — 35% и 3-й завод — 40% всей производимой продукции. Брак составляет 5% от продукции 1-го завода, 3% от продукции 2-го и 4% от продукции 3-го завода.
Вся продукция смешивается и поступает в продажу. Найти а) вероятность купить бракованное изделие; б) условную вероятность того, что купленное изделие изготовлено 1-м заводом, если это изделие бракованное.
Первая вероятность равна доле бракованных изделий в объеме всей продукции, то есть
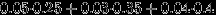 . Вторая вероятность равна доле брака 1-го завода среди всего брака, то есть
. Вторая вероятность равна доле брака 1-го завода среди всего брака, то есть 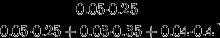
Определение 18.
Набор попарно несовместных событий
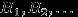 таких, что
таких, что 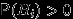 для всех
для всех 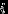 и
и 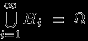 , называется полной группой событий или разбиением пространства
, называется полной группой событий или разбиением пространства 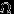 .
. События
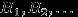 , образующие полную группу событий, часто называют гипотезами. При подходящем выборе гипотез для произвольного события
, образующие полную группу событий, часто называют гипотезами. При подходящем выборе гипотез для произвольного события 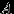 могут быть сравнительно просто вычислены
могут быть сравнительно просто вычислены 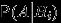 (вероятность событию
(вероятность событию 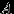 произойти при выполнении «гипотезы»
произойти при выполнении «гипотезы» 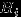 ) и собственно
) и собственно 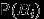 (вероятность выполнения «гипотезы»
(вероятность выполнения «гипотезы» 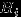 ). Как, используя эти данные, посчитать вероятность события
). Как, используя эти данные, посчитать вероятность события 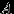 ?
? Теорема 8 (формула полной вероятности).
Пусть
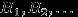 — полная группа событий. Тогда вероятность любого события
— полная группа событий. Тогда вероятность любого события 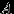 может быть вычислена по формуле:
может быть вычислена по формуле: 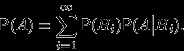
Доказательство.
Заметим, что
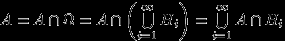 , и события
, и события 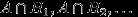 попарно несовместны. Поэтому (используем в первом равенстве
попарно несовместны. Поэтому (используем в первом равенстве  -аддитивность вероятностной меры (а что это?), а во втором — теорему умножения)
-аддитивность вероятностной меры (а что это?), а во втором — теорему умножения) 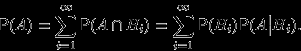
Q.D.E.

4.4. Формула Байеса
Теорема 9 (формула Байеса: Thomas Bayes).
Пусть
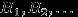 — полная группа событий и
— полная группа событий и 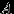 — некоторое событие положительной вероятности. Тогда условная вероятность того, что имело место событие
— некоторое событие положительной вероятности. Тогда условная вероятность того, что имело место событие 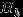 , если в результате эксперимента наблюдалось событие
, если в результате эксперимента наблюдалось событие 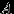 , может быть вычислена по формуле:
, может быть вычислена по формуле: 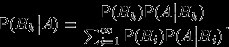
Доказательство.
По определению условной вероятности,
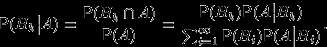
Последнее равенство следует из теоремы умножения и формулы полной вероятности.
Q.D.E.
Пример 19.
Вернемся к примеру 18. Изделие выбирается наудачу из всей произведенной продукции. Рассмотрим три гипотезы:
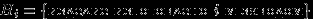 ,
,  . Вероятности этих событий даны:
. Вероятности этих событий даны: 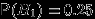 ,
, 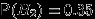 ,
, 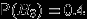 . Пусть
. Пусть 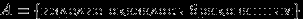 . Даны также условные вероятности
. Даны также условные вероятности 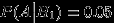 ,
, 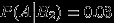 ,
, 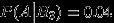 .
. Убедиться, что полученные нами вероятности в (а) и (б) совпадают с вероятностями, вычисленными по формуле полной вероятности и формуле Байеса.
Пример 20.
Два стрелка подбрасывают монетку и выбирают, кто из них стреляет по мишени (одной пулей). Первый стрелок попадает по мишени с вероятностью 1, второй стрелок — с вероятностью 0.00001. Можно сделать два предположения об эксперименте:
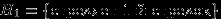 и
и 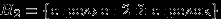 . Априорные (a'priori — «до опыта») вероятности этих гипотез одинаковы:
. Априорные (a'priori — «до опыта») вероятности этих гипотез одинаковы: 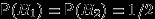 .
. Рассмотрим событие
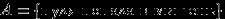 . Известно, что
. Известно, что 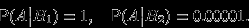
Поэтому вероятность пуле попасть в мишень
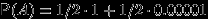 . Предположим, что событие
. Предположим, что событие 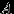 произошло. Какова теперь апостериорная (a'posteriori — «после опыта») вероятность каждой из гипотез
произошло. Какова теперь апостериорная (a'posteriori — «после опыта») вероятность каждой из гипотез 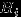 ?
? Очевидно, что первая из этих гипотез много вероятнее второй (а именно, в 100000 раз). Действительно,