Программа обсуждена на заседании кафедры Математики фнти

Вид материала

Программа

Содержание Распределения вероятностей Закон больших чисел. Предельные теормы Элементы статистики Случайные процессы Список литературы Дополнительная литература

Подобный материал:

• Программа обсуждена на заседании кафедры Математики фнти, 45.15kb.
• Программа обсуждена на заседании кафедры Математики фнти, 51.85kb.
• Программа обсуждена на заседании кафедры Математики фнти, 29.91kb.
• Программа обсуждена на заседании кафедры Математики фнти, 38.01kb.
• Программа обсуждена на заседании кафедры Математики фнти, 27.07kb.
• Программа обсуждена на заседании кафедры Математики фнти, 80.49kb.
• Программа обсуждена на заседании кафедры Математики фнти, 43.63kb.
• Программа обсуждена на заседании кафедры Математики фнти, 28.33kb.
• Программа обсуждена на заседании кафедры Математики фнти, 45.62kb.
• Программа обсуждена на заседании кафедры Математики фнти, 58.04kb.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

высшего профессионального образования

Московский физико-технический институт

(государственный университет)


УТВЕРЖДАЮ

Проректор по учебной работе

____________Ю.А. Самарский

__________________2008 г.


П Р О Г Р А М М А


по курсу:  ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

по направлению  511600

факультет  ФНТИ

кафедра  МАТЕМАТИКИ ФНТИ

курс 4

семестр 7

лекции   32 часа Экзамен  НЕТ

практические(семинарские)

занятия   32 часа Зачет  7 семестр

лабораторные занятия – нет Самостоятельная работа

 2 часа в неделю

Всего часов   64


Программу составил д.ф.-м.н., проф. А.М. Чеботарев

Программа обсуждена на заседании

кафедры Математики ФНТИ

25 декабря 2007 года


Заведующий кафедрой С.Ю. Доброхотов


Распределения вероятностей

1. Вероятностное пространство. Несовместные и независимые события. Формула полной вероятности в дискретном случае. Условная вероятность. Формула Байеса. Случайные величины, их средние значения, дисперсии и моменты высших порядков. Характеристические и производящие функции случайных величин. Корреляционные и ковариационные функции.
   
2. Биномиальное, пуассоновское и нормальное распределение. Гамма распределение. Сходимость биномиального распределения к пуассоновскому и нормальному.
   

Закон больших чисел. Предельные теормы

3. Неравенство Чебышева. Закон больших чисел. Преобразования и моделирование случайных величин. Метод обратной функции распределения и метод отбора Неймана.
   
4. Положительная определенность характеристических функций и теорема Шура. Теорема Бохнера--Хинчина. Центральная предельная теорема.
   
5. Распределения с тяжелыми хвостами и центральная предельная теорема для распределений Леви. Проблема моментов и теорема Бернштейна.
   

Элементы статистики

6. Обработка экспериментальных данных и задачи математической статистики. Выборочное среднее и несмещенная оценка дисперсии. Оценки выборочного среднего и распределения хи-квадрат и Стьюдента. Теорема Пирсона. Проверка гипотез и оценки доверительного интервала.
   
7. Применение критерия хи-квадрат для проверки гипотезы о независимости и распределения Стьюдента для проверки гипотезы о равенстве средних значений. Оценки выборочных дисперсий с помощью распределения Фишера.
   
8. Критерий Колмогорова для идентификации выборочных куммулятивных распределений. Статистические свойства распределений с тяжелыми хвостами.
   
9. Линейный метод наименьших квадратов. Оценки доверительных интервалов для коэффициентов линейной регрессии с помощью распределений Стьюдента и Фишера. Предельные оценки для большого числа наблюдений.
   
10. Вариационный ряд. Теорема Гливенко. Оценивание неизвестных параметров. Ошибки первого и второго рода. Состоятельные оценки и. достаточные статистики. Неравенство Рао – Крамера и эффективные оценки.
    

Случайные процессы

11. Марковские цепи и случайные блуждания. Принцип отражения Андрэ и другие оценки распределения времени первого достижения. Закон арксинуса. Классификация состояний. Теорема Перрона—Фробениуса и ее обобщения.
    
12. Пуассоновский процесс и сходимость случайных блужданий к винеровскому процессу. Представление стандартного винеровского процесса рядом Фурье со случайными коэффициентами.
    
13. Прямое и обратное уравнения Колмогорова—Феллера. Уравнение теплопроводности. Формулы Ито. Моменты первого достижения и стохастические представления решений уравнения теплопроводности. Абсолютно непрерывные преобразования меры Винера: формулы Фейнмана—Каца и Гирсанова.
    
14. Алгоритмы Метрополиса и Хастингса для моделирования случайных величин. Условие детального баланса. Случай марковских цепей с дискретным и непрерывным множеством состояний. Вычисление средних значений наблюдаемых величин по каноническому и большому каноническому ансамблям.
    

СПИСОК ЛИТЕРАТУРЫ

1. Худсон Д. Статистика для физиков. -М.: Мир, 1967.
   
2. Феллер В. Введение в теорию вероятностей и ее приложения. Том 1--2, -М.:, Мир, 1967.
   
3. Кельберт М.Я., Сухов Ю.М. Основные понятия теории вероятностей и математической статистики. Вероятность и статистика в примерах и задачах. -М.: МЦНМО, 2007.
   

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. Секей Г. Парадоксы теории вероятностей. – М.: Мир, 1990.
   
2. Ширяев А.Н. Вероятность. – М.: Наука, 1980.
   
3. Живописцев Ф.А., Иванов В.А. Регрессионный анализ в экспериментальной физике. – М.: МГУ, 1995.
   
4. Биндер К., Хеерман Д.В. Моделирование методом Монте-Карло в статистической физике. – М.: Наука, Физматлит, 1995.
   

Задания для самостоятельной работы

Пример Задания 1.


1. Показать, что в серии из N независимых наблюдений д.с.в. X с распределением P{X < x} = f(x) "экстремальное" событие

{X > x*_N}, где x*_N: f(x*_N)) = 1 - N^-1, происходит в среднем 1 раз.


2. Пусть p(x) и f(x)=P{X < x} –плотность и CPF д.с.в. X соответственно. Показать, что среднее значение максимума X_n в сериях из N наблюдений равно

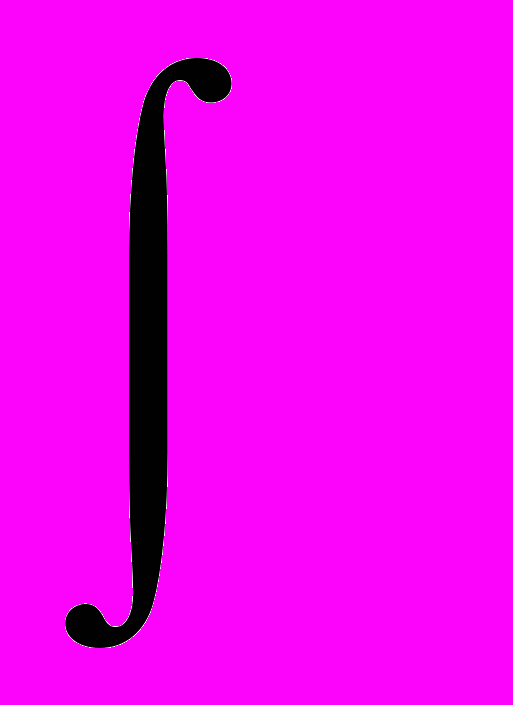_max> = E max{X₁, …. , X_N} = N dx x p(x) f(x)^N-1

4. Пусть {X₁, … ,X_n, …} –независимые выборочные значения случайной величины X {0,M}, имеющей биномиальное распределение P{X_n=m}= p^m (1 - p)^{M - m} . Показать, что X_n / M и X_n/ M (1-X_m / M), m 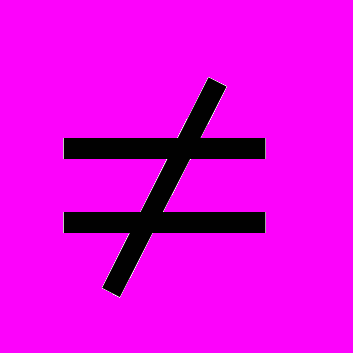n, можно использовать как несмещенные выборочные оценки p и p (1 - p) соответственно.
   

5. Используя формулу Бернштейна проверить достаточные условия существования вероятностного распределения и найти его, если известны соответствующие моменты
   
   1. _n = (n+1)^-1 , (b) _n = 2 (n+2)^-1, (c) _n = xⁿ , x (0,1).
      

6. При измерениях распределения энергии космического гамма-излучения в четырех фиксированных диапазонах в северном и южном полушариях по результатам наблюдений в течение некоторого отрезка времени было зарегистрировано N=1000 гамма-квантов:
   

E	Север	Юг
20-50 keV	350	340
50-100 keV	270	290
keV	200	190
> 300 keV	180	180

Гипотеза состоит в том, что распределение излучения изотропно, то есть вероятности наблюдения частиц с энергиями в указанных интервалах одинаково в северном и южном полушариях, а отклонения случайны.


Пример Задания 2.


1. Найти эргодическое распределение для стохастической (5 x 5) - матрицы


{{0.35025809808107783, 0.0307884571834019, 0.0452099582806349, 0.09943227854051748, 0.010665597942302577},

{0.11461240867206819, 0.313181597815516, 0.03937085571602794, 0.17751198802818535, 0.3612425761743832},

{0.35376590308475653, 0.06563633866527638, 0.32854077797952086, 0.09754978848341793, 0.2827870469779998},

{0.13224132363124977, 0.28553861874475667, 0.39232383978108515, 0.4309504356166369, 0.20180781640181397},

{0.049122266530847836, 0.30485498759104906, 0.1945545682427311, 0.19455550933124238, 0.1434969625035005}}


2. С помощью критерия Колмогорова проверить, являются ли 30 случайных точек из массива


X={-1.85225,-1.70679,-1.68897,-1.48966,-1.35345,-1.18571,-1.17253,-0.690791,-0.494714,-0.47646,-0.397319,-0.339439,-0.257418,-0.110735,-0.0297468, 0.119012, 0.157411, 0.183514, 0.229726, 0.333478, 0.351108, 0.381902, 0.743634,0.894862, 0.976229, 1.19951,1.27341, 1.59195, 1.61547, 1.77234, 1.83186,2.73349}


выборочными значениями стандартного нормального распределения для уровня значимости 5 %.

3. Для данных
   

X= {0.,0.05,0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45,0.5,0.55,0.6,0.65,0.7,0.75,0.8,0.85,0.9,0.95,1.}


Y = {1.02001,0.980672,0.880827,0.849228,0.813337,0.743418, 0.706255,0.667488,0.622742,0.552499,0.466238,0.437653,0.383927,0.316412, 0.356718,0.2391,0.214415,0.178742,0.0883751, 0.0665332, -0.0416756}


методом наименьших квадратов найти коэффициенты линейной регрессии y=b₀+b₁ x и найти доверительные интервалы для коэффициентов b₀, b₁ с уровнем значимости 5%.

3. Пусть {X_n}_n=1…N - случайные величины, {X₁, X₂, …. , X_N } -цепь Маркова с матрицей переходных вероятностей P=||p_ij||,
   

P {X₁, …. , X_N } = _k<N p_Xk,_X{k+1}.

Будет ли последовательность {X_N,X_N-1, … , X₁} марковской цепью?


5. Пусть {X_n}_n=1…N - случайные величины, {X₁, X₂, …. , X_N } -цепь Маркова с матрицей переходных вероятностей P=||p_ij||,

P {X₁, …. , X_N } = _k<N p_Xk,_X{k+1}

и f – некоторая функция. Будет ли последовательность {f(X₁),f(X₂), …., f(X_N)} марковской цепью?


6. Показать, что функция Метрополиса f(x)= min{1,x} является максимальной в классе функций f : R [0,1], совместных с уравнением детального баланса.


Срок сдачи 1-го задания: 10.10.2008 – 15.10.2008 г.

Срок сдачи 2-го задания: 05.12.2008 – 10.12.2008 г.


Усл. печ. л. . Уч.-изд.л. .