Geum.ru

Программа обсуждена на заседании кафедры Математики фнти

Вид материалаПрограмма

Содержание


Фундаментальные решения
Асимптотические методы
Список основной литературы
Список дополнительной литературы
Подобный материал:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ


Государственное образовательное учреждение

высшего профессионального образования

Московский физико-технический институт

(государственный университет)


УТВЕРЖДАЮ

Проректор по учебной работе

Ю.А. Самарский

____________________2008 г.


П Р О Г Р А М М А


по курсу:  УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

по направлению  511600

факультет  ФНТИ

кафедра  МАТЕМАТИКИ ФНТИ

курс III

семестр 6

лекции  32 часа Экзамен  6 семестр

практические(семинарские)

занятия   32 часа Зачет нет

лабораторные занятия – нет Самостоятельная работа

  2 часа в неделю

Всего часов  64


Программу составили д.ф.-м.н., проф. В.В. Белов

д.ф.-м.н., проф. С.Ю. Доброхотов

Программа обсуждена на заседании

кафедры Математики ФНТИ

25 декабря 2007 года


Заведующий кафедрой С.Ю. Доброхотов

Фундаментальные решения

1. Фундаментальное решение для уравнения Гельмгольца в (полу)пространстве. Условие излучения Зоммерфельда. Формула Кирхгофа. Постановки задач дифракции и рассеяния (плоской волны и от точечного источника).

2. Фундаментальное решение (функция Грина) и решение задачи Коши для неоднородных волнового уравнения и уравнения теплопроводности в пространстве. Формулы Даламбера, Кирхгофа и Пуасcона. Принцип Дюамеля для волнового уравнения. Корректность задачи Коши. Распространение волн в пространстве и принцип Гюйгенса.

3. Понятие обобщенных (слабых) решений задачи Коши для волнового уравнения. Выделение сингулярных частей (разрывов) обобщенных решений волнового уравнения в неоднородной среде методом Лакса (разложение «по гладкости»).


Асимптотические методы

4. Приближенные (асимптотические) методы решения уравнений математической физики. Квазиклассическое приближение для многомерного нестационарного уравнения Шредингера (метод ВКБ). «Катастрофы» в решении и особенности функции Грина. Коротковолновое приближение (лучевые разложения) для волнового уравнения и уравнения Гельмгольца в неоднородной среде. Метод стационарной фазы (вывод формул методом ВКБ для гармонического осциллятора — операция обхода фокусов). Квазиклассическая асимптотика функции Эйри.

5. Стандартные и нестандартные (В. П. Маслов) характеристики линейных уравнений с частными производными второго порядка. Классификация уравнений, включающая уравнения квантовой механики (Шредингера и Клейна–Гордона–Фока).


СПИСОК ОСНОВНОЙ ЛИТЕРАТУРЫ

  1. Тихонов А. Н., Самарский А. А. Уравнения математической физики.  М.: Наука, 1977.
  2. Владимиров В.С. Уравнения математической физики.  М.: Наука, 1983.

3. Багров В. Г., Белов В. В., Задорожный В.Н., Трифонов А. Ю. Методы математической физики. IV. Уравнения математической физики.  Томск: Изд-во НТЛ, 2002.

4. Белов В. В., Доброхотов С. Ю., Синицын С. О. Конспекты лекций по математическим методам физики. Тетрадь 1. Уравнения в частных производных первого порядка: аналитическая и геометрическая теория. Элементы теории катастроф.  Уч. пособие под редакцией В. В. Белова и С. Ю. Доброхотова.  М.: Издательско-производственный комплекс ФГУ РНЦ «Курчатовский институт», 2004.

5. Белов В. В., Воробьев Е. М. Сборник задач по дополнительным главам математической физики.  М.: Высшая школа, 1978.

6. Владимиров В. С., Михайлов В. П., Вашарин А. А., Каримова Х. Х., Сидоров Ю. В., Шабунин М. И. Сборник задач по уравнениям математической физики.  2-е изд.  М.: Наука, 1982.


СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ

  1. Петровский И. Г. Лекции об уравнениях с частными производными первого порядка.  М.: Наука, 1970.
  2. Шварц Л. Математические методы для физических наук.  М.: Мир, 1965.
  3. Маслов В. П., Федорюк М. В. Квазиклассическое приближение для уравнений квантовой механики.  М.: Наука, 1976.
  4. Бабич В. М., Булдырев В. С. Асимптотические методы в задачах дифракции коротких волн.  М.: Наука, 1972.



В курсе предусмотрены 2 домашних задания (номера даны по задачнику [5] в списке основной литературы) и лабораторный практикум.


1-е домашнее задание выдается на 1-й неделе, оно содержит задачи по 1-й теме Срок сдачи – 6-я неделя. Задачи: 3.1, 3.4;


2-е домашнее задание выдается на 11-й неделе, оно содержит задачи по 2-й теме. Срок сдачи – 16-я неделя. Задачи: I-1, I-2, V-1, V-3, V-5.


Лабораторный практикум (в период с 7 по 10 неделю)


Применение программ Mathematica или MATLAB при решении следующих задач по задачнику [5]: 1.5, 1.6 2) (визуализация профиля волны и интегральных поверхностей); V-5 (построить эволюцию лагранжевой кривой при 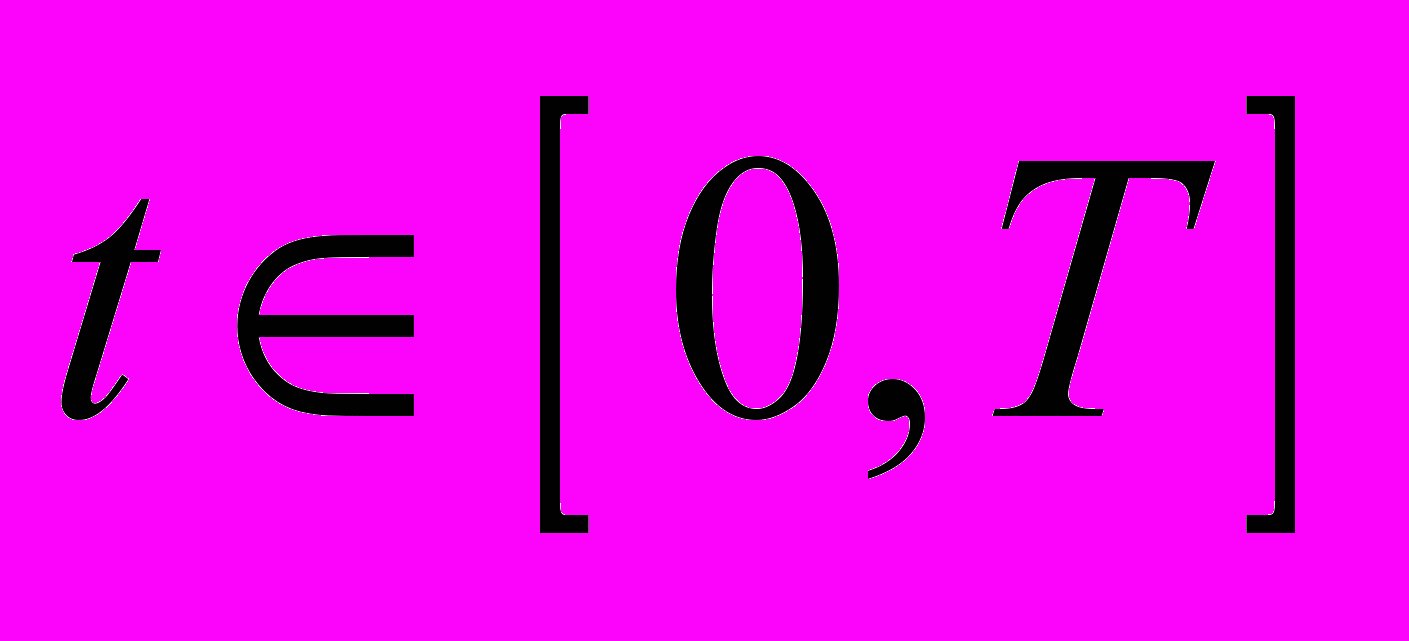, где 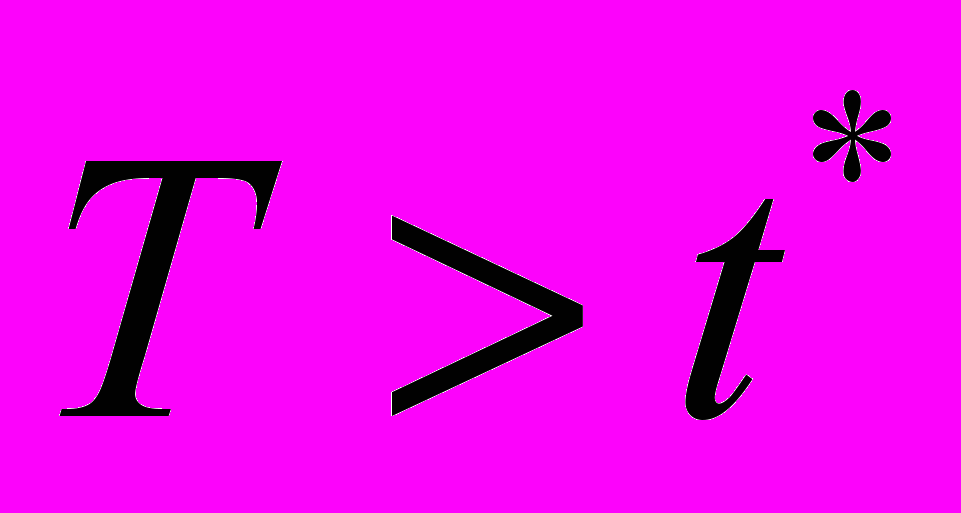, 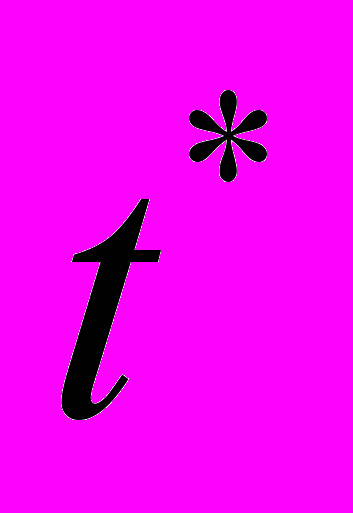– начало развития катастрофы в ВКБ-решении);


Усл. печ. л. Тираж