Вероятность произведения событий. Условная вероятность
| Вид материала | Документы |
- Основные простейшие теоремы теории вероятностей, 32.04kb.
- Программа курса лекций, 26.81kb.
- Лекция Условная вероятность, независимость, 67.33kb.
- Контрольная работа №4. по дисциплине «ТВиМС», 25.55kb.
- Лекция Управление рисками проекта, 216.18kb.
- Курс «Вероятность» является вторым в ряду вероятностно-эконометрических курсов Вероятность, 32.07kb.
- Основные виды случайных величин, 49.77kb.
- Введение, 58.17kb.
- Томский Государственный Университет Систем Управления и Радиоэлектроники (тусур) Томский, 19.19kb.
- Программа обсуждена на заседании кафедры Математики фнти, 75.2kb.
^ Условные распределения случайных величин
Если две случайные величины и зависимы, то информация о том, какое значение на самом деле приняла одна из них, меняет наше представление о распределении другой. В связи с этим можно ввести понятие условного распределения.
^ Условные распределения дискретных случайных величин
Пусть дана двумерная случайная величина ( , ) с распределением
| | y1 | y2 | ... | ym |
| x1 | p11 | p12 | ... | p1m |
| x2 | p12 | p12 | ... | p2m |
| ... | ... | ... | pij | ... |
| xn | pn1 | pn2 | ... | pnm |
Тогда распределения случайных величин и имеют соответственно вид:
| | x1 | x2 | ... | xn |
| p | p1 | p2 | ... | pn |
| | y1 | y2 | ... | yn |
 | p 1 | p 2 | ... | p n |
точка в индексе означает суммирование по строкам или по столбцам:
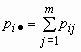 ,
, 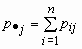 .
.Условным распределением случайной величины
 при условии, что случайная величина
при условии, что случайная величина 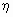 приняла значение
приняла значение 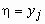 , называется распределение:
, называется распределение:| | x1 | x2 | ... | xn |
| p | 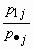 | 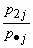 | ... | 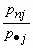 |
Нетрудно убедиться, что сумма вероятностей величины
 в этом распределении равна единице:
в этом распределении равна единице: 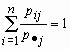 для всех j = 1, 2, …, m.
для всех j = 1, 2, …, m.Совершенно аналогично условным распределением случайной величины
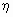 при условии, что случайная величина
при условии, что случайная величина  приняла значение
приняла значение  , называется распределение:
, называется распределение:| | y1 | y2 | ... | yn |
| p | 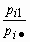 |  | ... |  |
И
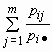 для всех i = 1, 2, …, n.
для всех i = 1, 2, …, n.Если условные распределения случайных величин и отличаются от их безусловных распределений, то случайные величины и зависимы.
^ Условные распределения непрерывных случайных величин
Если
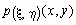 - плотность вероятностей совместного распределения двумерной случайной величины
- плотность вероятностей совместного распределения двумерной случайной величины 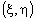 , то плотности вероятностей каждой ее компоненты вычисляются по формулам:
, то плотности вероятностей каждой ее компоненты вычисляются по формулам: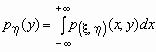 ,
, 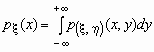 .
.^ Условной плотностью распределения случайной величины при условии, что случайная величина принимает значение = y0, называется функция переменной x, определяемая формулой
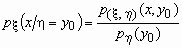 .
.Аналогично, условной плотностью распределения случайной величины
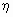 при условии, что случайная величина принимает значение = x0, называется функция переменной y, определяемая формулой
при условии, что случайная величина принимает значение = x0, называется функция переменной y, определяемая формулой .
.^ Плотность вероятности суммы двух случайных величин ~ Распределение произведения двух случайных величин
Если - случайная величина с областью значений X и функция f(x) определена на множестве X , то = f(x) - тоже случайная величина. Задача об отыскании функции распределения случайной величины по известной функции распределения случайной величины легко решается, если f(x) - непрерывная монотонно возрастающая функция. Доказано, что тогда функция распределения F (x) случайной величины задается формулой F (x)=F ([f(x)]-1).
Здесь F (x) - известная функция распределения случайной величины , а символом [f(x)]-1 обозначена функция, обратная к функции f(x).
Плотность распределения случайной величины для дифференцируемой f(x) вычисляется по формуле
 .
.^ Плотность вероятности суммы двух случайных величин
В теории вероятностей часто возникает необходимость в определении плотности вероятности суммы двух независимых случайных величин. Если 1 и 2 - непрерывные независимые случайные величины с плотностями вероятности соответственно p1(x) и p2(x), то плотность вероятностей суммы = 1 + 2 вычисляется по формуле:
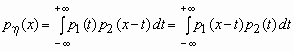 .
.^ Распределение произведения двух случайных величин
Порядок построения распределения произведения двух дискретных случайных величин проще всего объяснить на примере.
Пусть ( , ) - дискретный случайный вектор с распределением:
| | 1 | 2 | 3 | 4 |
| 0 | 0.01 | 0.02 | 0.03 | 0.04 |
| 1 | 0.1 | 0.1 | 0.2 | 0.4 |
| 2 | 0.05 | 0.01 | 0.01 | 0.03 |
Найдем распределение произведения случайных величин - случайной величины = ,
которая принимает значения 0, 1, 2, 3, 4, 6, 8. Вычислим соответствующие вероятности:
P( = = 0) = P( = 0, = 1) + P( = 0, = 2) + P( = 0, = 3) + P( = 0, = 4) = 0.1;
P( = 1) = P( = 1, = 1) =0.1; P( = 2) = P( = 1, = 2) + P( = 2, = 1) =0.15; и т.д.
В результате получим распределение случайной величины = :
 | 0 | 1 | 2 | 3 | 4 | 6 | 8 |
| p | 0.1 | 0.1 | 0.15 | 0.2 | 0.41 | 0.01 | 0.03 |
Для того чтобы найти распределение произведения непрерывных случайных величин, необходимо выполнить более громоздкие вычисления.
Пусть ( , ) - непрерывный двумерный случайный вектор с плотностью распределения p( )(x1, x2). Построим функцию распределения случайной величины = . Согласно определению
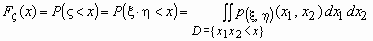 .
.Для вычисления этой вероятности рассмотрим отдельно случаи x>0 и x<0. Области интегрирования для обоих случаев на рисунке закрашены.
Область D={ x1x2 < x, x > 0} изображена на рисунке слева, а область D={ x1x2 < x, x < 0} - справа.
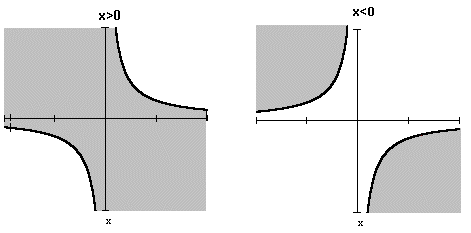
При x>0 имеем:
 .
.При x<0:
 .
.^ Математическое ожидание ~ Дисперсия ~ Условное математическое ожидание ~ Ковариация ~ Корреляция
В этом разделе рассмотрены числовые характеристики только двумерных случайных величин, поскольку обобщение на случай
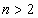 не вызывает затруднений.
не вызывает затруднений.^ Математическое ожидание
Пусть ( , ) - двумерная случайная величина, тогда M( , )=(M( ), M( )), т.е. математическое ожидание случайного вектора - это вектор из математических ожиданий компонент вектора.
Если ( , ) - дискретный случайный вектор с распределением
| | y1 | y2 | ... | ym |
| x1 | p11 | p12 | ... | p1m |
| x2 | p12 | p12 | ... | p2m |
| ... | ... | ... | pij | ... |
| xn | pn1 | pn2 | ... | pnm |
то математические ожидания компонент вычисляются по формулам:
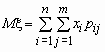 ,
, 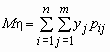 .
.Эти формулы можно записать в сокращенном виде.
Обозначим
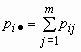 и
и 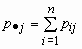 , тогда
, тогда 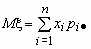 и
и  .
.Если p( , )(x, y)- совместная плотность распределения непрерывной двумерной случайной величины ( , ), то
 и
и 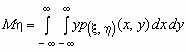 .
.Поскольку
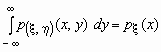 -плотность распределения случайной величины , то
-плотность распределения случайной величины , то  и, аналогично,
и, аналогично,  .
.Дисперсия
Понятие дисперсии обобщается на многомерные случайные величины нетривиальным образом. Это обобщение будет сделано в следующем разделе. Здесь лишь приведем формулы для вычисления дисперсии компонент двумерного случайного вектора.
Если ( , ) - двумерная случайная величина, то
D = M( - M )2 = M 2 - M( )2, D = M( - M )2 = M 2 - M( )2.
Входящие в эту формулу математические ожидания вычисляются по приведенным выше формулам.
^ Условное математическое ожидание
Между случайными величинами может существовать функциональная зависимость. Например, если - случайная величина и = 2, то - тоже случайная величина, связанная с функциональной зависимостью. В то же время между случайными величинами может существовать зависимость другого рода, называемая стохастической. В разделе, посвященном условным распределениям уже обсуждалась такая зависимость. Из рассмотренных там примеров видно, что информация о значении одной случайной величины (одной компоненты случайного вектора) изменяет распределение другой случайной величины (другой компоненты случайного вектора), а это может, вообще говоря, изменить и числовые характеристики случайных величин.
Математическое ожидание, вычисленное по условному распределению, называется условным математическим ожиданием.
Для двумерного дискретного случайного вектора ( , ) с распределением
| | y1 | y2 | ... | ym |
| x1 | p11 | p12 | ... | p1m |
| x2 | p12 | p12 | ... | p2m |
| ... | ... | ... | pij | ... |
| xn | pn1 | pn2 | ... | pnm |
условное математическое ожидание случайной величины при условии, что случайная величина принимает значение yj, вычисляется по формуле
 .
.Аналогично, условное математическое ожидание случайной величины при условии, что случайная величина принимает значение xi, равно
 .
.Видно, что условное математическое ожидание случайной величины является функцией значений случайной величины , т.е. M( / = y) = f1(y) и, совершенно аналогично, M( / = x) = f2(x).
Функцию f1(y) называют регрессией случайной величины на случайную величину , а f2(x) - регрессией случайной величины на случайную величину .
Если p( , )(x, y) совместная плотность вероятностей двумерной случайной величины ( , ), то
 и
и  .
. 