Вероятность произведения событий. Условная вероятность

Вид материала

Документы

Содержание Ковариационной матрицей случайного вектора Неравенство Чебышева Теорема Пуассона Центральная предельная теорема Закон больших чисел Теорема Ляпунова

Подобный материал:

• Основные простейшие теоремы теории вероятностей, 32.04kb.
• Программа курса лекций, 26.81kb.
• Лекция Условная вероятность, независимость, 67.33kb.
• Контрольная работа №4. по дисциплине «ТВиМС», 25.55kb.
• Лекция Управление рисками проекта, 216.18kb.
• Курс «Вероятность» является вторым в ряду вероятностно-эконометрических курсов Вероятность, 32.07kb.
• Основные виды случайных величин, 49.77kb.
• Введение, 58.17kb.
• Томский Государственный Университет Систем Управления и Радиоэлектроники (тусур) Томский, 19.19kb.
• Программа обсуждена на заседании кафедры Математики фнти, 75.2kb.

Ковариация

 

Если между случайными величинами  и  существует стохастическая связь, то одним из параметров, характеризующих меру этой связи является ковариация cov( ,  ). Ковариацию вычисляют по формулам cov( ,  )=M[( - M )( - M )]  M( ) - M M .

Если случайные величины  и  независимы, то cov( , )=0.

Обратное, вообще говоря, неверно. Из равенства нулю ковариации не следует независимость случайных величин. Случайные величины могут быть зависимыми в то время как их ковариация нулевая! Но зато, если ковариация случайных величин отлична от нуля, то между ними существует стохастическая связь, мерой которой и является величина ковариации.

Свойства ковариации:

cov( ,  ) = D ;

 

;

;

,

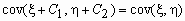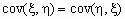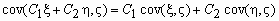где C₁ и C₂ - произвольные константы.

^ Ковариационной матрицей случайного вектора ( , ) называется матрица вида

.

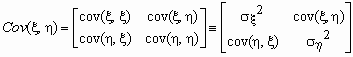Эта матрица симметрична и положительно определена. Ее определитель называется обобщенной дисперсией и может служить мерой рассеяния системы случайных величин ( , ).

Как уже отмечалось ранее, дисперсия суммы независимых случайных величин равна сумме их дисперсий: 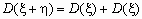. Если же случайные величины зависимы, то .

 

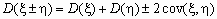Корреляция

 

Понятно, что значение ковариации зависит не только от “тесноты” связи случайных величин, но и от самих значений этих величин, например, от единиц измерения этих значений. Для исключения этой зависимости вместо ковариации используется безразмерный коэффициент корреляции .

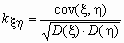Этот коэффициент обладает следующими свойствами:

он безразмерен;

его модуль не превосходит единицы, т.е. ;

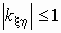если  и  независимы, то k_{( , )}=0 (обратное неверно!);

если 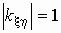, то случайные величины  и  связаны функциональной зависимостью вида

 = a +b,

где a и b- некоторые числовые коэффициенты;

;

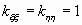Корреляционной матрицей случайного вектора называется матрица

.

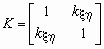Есл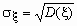и и 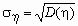, то ковариационная и корреляционная матрицы случайного вектора ( , ) связаны соотношением 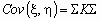, где .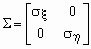


^ Неравенство Чебышева ~ Теорема Бернулли ~ Центральная предельная теорема. ~ Закон больших чисел ~ Теорема Ляпунова

 

Практика изучения случайных явлений показывает, что хотя результаты отдельных наблюдений, даже проведенных в одинаковых условиях, могут сильно отличаться, в то же время средние результаты для достаточно большого числа наблюдений устойчивы и слабо зависят от результатов отдельных наблюдений.

Теоретическим обоснованием этого замечательного свойства случайных явлений является закон больших чисел. Названием "закон больших чисел" объединена группа теорем, устанавливающих устойчивость средних результатов большого количества случайных явлений и объясняющих причину этой устойчивости.

Простейшая форма закона больших чисел, и исторически первая теорема этого раздела - теорема Бернулли, утверждающая, что если вероятность события одинакова во всех испытаниях, то с увеличением числа испытаний частота события стремится к вероятности события и перестает быть случайной.

^ Теорема Пуассона утверждает, что частота события в серии независимых испытаний стремится к среднему арифметическому его вероятностей и перестает быть случайной.

Предельные теоремы теории вероятностей, теоремы Муавра-Лапласа объясняют природу устойчивости частоты появлений события. Природа эта состоит в том, что предельным распределением числа появлений события при неограниченном возрастании числа испытаний (если вероятность события во всех испытаниях одинакова) является нормальное распределение.

^ Центральная предельная теорема объясняет широкое распространение нормального закона распределения. Теорема утверждает, что всегда, когда случайная величина образуется в результате сложения большого числа независимых случайных величин с конечными дисперсиями, закон распределения этой случайной величины оказывается практически нормальным законом.

Теорема, приведенная ниже под названием "^ Закон больших чисел" утверждает, что при определенных, достаточно общих, условиях, с увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным.

^ Теорема Ляпунова объясняет широкое распространение нормального закона распределения и поясняет механизм его образования. Теорема позволяет утверждать, что всегда, когда случайная величина образуется в результате сложения большого числа независимых случайных величин, дисперсии которых малы по сравнению с дисперсией суммы, закон распределения этой случайной величины оказывается практически нормальным законом. А поскольку случайные величины всегда порождаются бесконечным количеством причин и чаще всего ни одна из них не имеет дисперсии, сравнимой с дисперсией самой случайной величины, то большинство встречающихся в практике случайных величин подчинено нормальному закону распределения.

В основе качественных и количественных утверждений закона больших чисел лежит неравенство Чебышева. Оно определяет верхнюю границу вероятности того, что отклонение значения случайной величины от ее математического ожидания больше некоторого заданного числа. Замечательно, что неравенство Чебышева дает оценку вероятности события 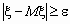для случайной величины, распределение которой неизвестно, известны лишь ее математическое ожидание и дисперсия.

 

Неравенство Чебышева. Если случайная величина  имеет дисперсию, то для любого  > 0 справедливо неравенство 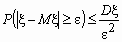, где M и D - математическое ожидание и дисперсия случайной величины  .

 

Теорема Бернулли. Пусть  _n - число успехов в n испытаниях Бернулли и p - вероятность успеха в отдельном испытании. Тогда при любом  > 0 справедливо .

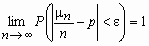Центральная предельная теорема. Если случайные величины  ₁,  ₂, …,  _n, … попарно независимы, одинаково распределены и имеют конечную дисперсию, то при n  равномерно по x (- , )

.

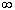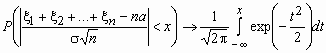Закон больших чисел. Если случайные величины  ₁,  ₂, …,  _n, … попарно независимы и 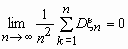,то для любого  > 0

.

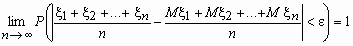Теорема Ляпунова. Пусть  ₁,  ₂, …,  _n, …- неограниченная последовательность независимых случайных величин с математическими ожиданиями m₁, m₂, …, m_n, … и дисперсиями  ₁²,  ₂², …,  _n²… . Обозначим , , ,.

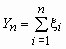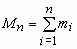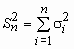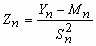Тогда 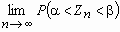  = Ф() - Ф() для любых действительных чисел  и  , где Ф(x) - функция распределения нормального закона.