Geum.ru

Лекции по курсу «композиция в технике»

Вид материалаЛекции

Содержание


Лекция 6. Средства композиции
Рис. 1.65. Симметричная композиция в ювелирном дизайне
Рис 1.67. Модель горизонтально-фрезерного станка первой половины XIX в.
Подобный материал:
1   2   3   4   5

Лекция 6. Средства композиции


Средства гармонизации (или средства соразмерности, поскольку формообразующие средства композиции – объемно-пространственная и тектоническая организация формы – также служат целям гармонизации) – общие для всех видов художественного творчества. К ним относятся симметрия, асимметрия, статика, динамика, пропорции, модуль, масштаб, контраст, нюанс, ритм, метрические повторы, а также группа средств, основанных на использовании цвета и тона, фактуры и текстуры материала и непосредственно связанной с ними светотеневой структуры формы. Рассмотрим подробнее средства композиции.

Симметрия и асимметрия

Симметричной называется всякая фигура, которая состоит из геометрически и физически равных частей, должным образом расположенных относительно друг друга. Под геометрическим равенством подразумевается совместимое (конгруэнтность) либо зеркальное равенство.

Существует три основных вида симметрии: зеркальная, осевая, винтовая.

Зеркальная симметрия подразумевает наличие оси и зеркальное, т. е. полное, отражение в одну и другую стороны. На рис. 1.65 показан пример зеркальной симметрии в ювелирном дизайне. Осевая симметрия обусловлена конгруэнтностью (равенством геометрических фигур в осевых сечениях) и достигается вращением фигуры относительно оси симметрии. Винтовая симметрия достигается в результате вращательного движения линии или плоскости вокруг неподвижной оси с постоянной угловой скоростью и одновременно поступательного движения вдоль оси. Спираль, винты, винтовые лестницы – вот наиболее простые случаи такой симметрии.

В природе абсолютной симметрии нет. Отступления от симметрии неизбежны и в технике, так как они обусловливаются функциональными и конструктивными факторами. Но они вполне допустимы, так как сами по себе не дезорганизуют форму. Однако в этих случаях асимметричные элементы необходимо органически увязать с остальным строем формы, композиционно уравновесить, и тогда симметричная в своей основе композиция с определенными отступлениями может стать упорядоченной.



Рис. 1.65. Симметричная композиция в ювелирном дизайне

При асимметричной композиции отдельные элементы лишены своей связующей – оси симметрии, поэтому работа над асимметричной формой сложнее, чем над симметричной. Соподчинение элементов формы в данном случае сводится к соблюдению композиционного равновесия.

Под композиционным равновесием понимается такое состояние формы, при котором все элементы сбалансированы между собой. Композиционное равновесие неадекватно простому равенству элементов и зависит от распределения основных масс композиции относительно ее центра (рис. 1.66). Понятие «центр композиции» в большинстве случаев трактуется как место сосредоточения основных, важнейших связей между всеми элементами, как правило, это и смысловой центр предмета. Оно связано с характером организации материала и пространства, пропорциями, расположением главной и второстепенной осей, с цветовыми и тональными отношениями частей целого.

В качестве примера рассмотрим один из случаев проявления и покажем особенности достижения гармонии с помощью этих средств композиции. На рис. 1.67 представлен пример проявления асимметрии в модели горизонтально-фрезерного станка. Элементы асимметричной композиции в данном случае не дезорганизуют форму станка, т. к. уравновешены и органически связаны с основной конструкцией – асимметричная часть повторяет основную конструкцию и логически не противоречива.




Рис. 1.66. Модель фрезерного станка для обработки деталей
оружейного замка первой четверти XIX в.
Тульский государственный музей оружия5



Рис 1.67. Модель горизонтально-фрезерного станка первой половины XIX в.6

Статичность и динамичность

Статичность – это подчеркнутое выражение состояния покоя, незыблемости, устойчивости формы. Статичны предметы, которые имеют явный центр и ось симметрии. В средствах транспорта статичность исключается, а в станках сочетаются статичные и движущиеся элементы.

Динамичной принято считать односторонне и активно направленную форму. Это свойство композиции связано с пропорциями и отношениями элементов формы. При равенстве отношений для нее характерна статичность, а при их контрасте – динамичность.

Статичность и динамичность связаны с характером работы изделия, с особенностями его функционирования (неподвижный или движущийся предмет) и зависят от связи изделия с другими элементами ансамбля, в который он входит.

Активная и односторонне направленная форма – необходимое условие проявления динамичности. Например, куб создает впечатление статичности, а вертикальный параллелепипед – динамичности. Но если параллелепипед положить, исчезает односторонняя направленность формы, и объем становится статичным.

Динамичность свойственна как неподвижным, так и быстродвижущимся предметам. В первом случае она является результатом конструктивной компоновки, следствием взаимодействия различных по размерам элементов, но не обусловливается требованиями эксплуатации. Поэтому для неподвижных предметов динамичность не является качеством, определяющим форму. Динамичность же формы быстродвижущихся предметов, например, средств транспорта, обусловлена функционально и определяется законами аэродинамики. В таких случаях она может стать главным качеством композиции, выражать сущность самого предмета.

В форме одного предмета очень важно правильно выразить динамичность. В технике встречаются случаи, когда часть предмета, например, несущая основа, является статичной, а другая, например подвижный механизм – динамичной. В таком случае выраженные по-разному части находятся в противоречии и гармония композиции нарушается.

Метро-ритмические соотношения

Гармонизации на основе метра и ритма предполагает установление закономерного порядка в расположении частей композиции. Чтобы такой порядок состоялся, в форме должно быть не менее трех элементов, хотя начало ему могут положить и два элемента. Каковы же объективные закономерности его установления?

Метр – простейший порядок, основанный на повторении равных элементов. Он подобен чередованию тактов в музыке (рис. 1.68). Повтор облегчает восприятие формы, делает ее четкой и ясной. Однако при большой протяженности метрическая композиция может выглядеть монотонной. Устранению монотонности способствует:
  • сочетание в композиции нескольких метрических рядов разного построения;
  • выделение в метрическом ряду групп элементов;
  • установление разрядок между группами;
  • «оживление» метрического ряда за счет включения в него акцентов;
  • изменение отдельных свойств повторяющихся элементов.




Рис 1.68. Метрический ряд как основа композиции.
Амстердам. Екатерина Гусева

Наиболее активным средством устранения монотонности в метрическом строе является его сочетание с ритмом или просто – ритмизация формы. В чем ее специфика?

Количество элементов и размеры пространства, в котором организуется метрическая композиция, могут быть различными. Если повторяющиеся элементы должны располагаться близко друг от друга, метрический ряд может оказаться перенасыщенным. Тогда элементам тесно, фон их не держит и повтор не воспринимается. Сохранить целостность ряда могут помочь нюансные решения элементов, например уменьшение насыщенности их цвета. Использование контрастных приемов, наоборот, будет способствовать перенасыщению композиции.

При разреженной композиции элементы ряда будут теряться. Чтобы повтор как закономерность смог выполнить свою организующую роль, элементы разреженного ряда должны быть сильными, предельно активными. Это особенно важно в тех случаях, когда метрический ряд является основой композиции. Если же повтор играет второстепенную роль, элементы можно не подчеркивать.

Роль метрического повтора особенно велика в тех дизайнерских разработках, где применяются унификация элементов и модульные сетки (рис. 1.69).





Рис. 1.69. Дизайн панели модема
с использованием метрических повторов

В технике метрический повтор или метр больше обусловливается конструктивными особенностями изделия. Но если необходимо организовать его форму, он может применяться как декоративное средство.

Ритм – более сложный, чем метр, порядок чередования элементов композиции. Он основан на неравномерном изменении их свойств. Это изменение может касаться как самих элементов, так и интервалов между ними. При постоянном их изменении образуется непрерывное множество, которое может носить разный характер – резко или плавно изменяющийся (рис. 1.70).




а б

Рис. 1.70. Ритмическая композиция:
а – спокойная, б – напряженная

Если одним из полюсов ритмического построения является приближающийся к равномерному строю строгий ритмический порядок, то другим – порядок, основанный на свободном расположении элементов. Второй полюс граничит с аритмией или хаотичным расположением разных по своим свойствам композиционных элементов, но не сводится к нему.

Ритм остается средством гармонизации при условии создания крайне динамичной, но все же собранной композиции. Элементы в нем, при кажущейся случайности расположения, определенным образом упорядочены. Если порядок вовсе отсутствует, композиция распадается.

Наиболее характерный прием построения ритма – изменение величины элементов. На таком изменении строятся нарастающие и убывающие ритмические ряды. Плавное нарастание ведет к построению «спокойной» ритмической композиции (рис. 1.70, а), резкое – «напряженной» (рис. 1.70, б). За чрезмерно резким изменением величины элементов кроется разрушение композиционно-ритмического строя. Другой распространенный прием – изменение интервалов между элементами. С его использованием связано построение сужающихся и расширяющихся ритмических рядов. Первые ряды образуются за счет сокращения расстояний между элементами, вторые – за счет их увеличения.

Степень изменения в данном случае будет определять замедление или ускорение ритма. Постепенное увеличение размеров интервалов ведет к зрительному утяжелению формы в направлении этого увеличения, и наоборот, уменьшение – к ее облегчению [1.17, с. 136]. Активность ритма в композиции зависит от силы проявления этой закономерности. Если изменения чередований незначительны, то проявление ритма выражено слабо. Наоборот, при явном чередовании элементов ритм может служить главным началом композиции. Многое зависит также от протяженности ряда. Ритмический ряд предполагает не менее четырех-пяти элементов, так как три еще не создают впечатления закономерного повтора.

При использовании ритма как средства композиции очень важно уметь правильно завершить ряд, иначе может возникнуть впечатление случайного его обрыва. В этом смысле задача решается сложнее, чем при использовании метрического повтора.

Как средство композиции ритм используется в дизайне в тех случаях, когда он объективно предопределен конструктивной основой. Проявления ритма в технике весьма разнообразны, например при членении корпуса какого-либо транспортного средства или при организации элементов на плоскости приборной панели, т. е. там, где нужно ориентировать форму в каком-либо направлении или расположить и организовать элементы формы с ритмической направленностью к главной оси, к композиционному центру.

Метр и ритм могут быть связаны, с одной стороны, с пропорциями, а с другой – с модульной сеткой. В дизайне в ряде случаев эта зависимость определяется жесткой связью метрических рядов с конструктивной системой. В средствах транспорта, например, возникает обусловленная их структурой конструктивная сетка, которая является своеобразным модулем, и от него уже зависят все метроритмические соотношения других элементов, находящихся внутри салона.

Метроритмические ряды способствуют выделению главного в композиции, выявлению характерных, особенно для динамических композиций, акцентов и их закономерного чередования с пассивными интервалами, служащими как бы фоном.

Модульная система

Модулем (лат. «modulos» – мера) – величина, размер, принимаемый за основу расчета размеров какого-то предмета, машины или сооружения. Совокупность правил расчета и модулей, используемых для этого расчета, носит название модульной системы.

В дизайне понятие «модуль» встречается в основном там, где деятельность дизайнера так или иначе связана с оборудованием помещений или изготовлением оборудования из унифицированных элементов.

Оборудование и мебель для жилища необходимо проектировать на основе единого модуля, который зависит от модуля архитектурного. Модульная координация находит применение также в приборостроении и в станкостроении, особенно там, где используются унификация и агрегатирование.

Пропорции и пропорционирование

Пропорция – соразмерность, определенное соотношение отдельных частей и предметов между собой. Размерные отношения элементов формы изделий служат той основой, на которой строится вся композиция.

В математической пропорции А : В = С : Д = ... = К каждый из членов тесно связан определенными соотношениями с остальными. Отсюда и возникает строгая согласованность входящих в пропорцию отдельных членов, их взаимосвязь и взаимообусловленность. И это обстоятельство широко используется не только и архитектуре и дизайне, но и во всех видах художественной деятельности, в которых так или иначе можно вести речь о соотношении каких-то элементов, каких-то линейных или объемных величин.

Как образуется самая элементарная пропорция? Из математики известно, что если взять две подобные фигуры, то соотношение аналогичных элементов в этих фигурах дает пропорциональный ряд.

Пропорционирование – это использование с целью получения искомой целостности предмета закономерных соотношений различных величин или частей предмета между собой.

Пропорции применительно к художественной деятельности предполагают сопоставление вертикальных и горизонтальных элементов в пределах определенной плоскости. Сложный предмет обычно заключают в какую-то простую фигуру-схему, например, параллелепипед, основные линейные величины которого и должны соотноситься, создавать какой-то определенный пропорциональный ряд. В этом и заключается их соразмерность.

Сочетание различных геометрически подобных элементов дает следующие виды пропорциональных отношений:
  • арифметические пропорции типа Н2 – Н1 = Н3 – Н2 и т. д.;
  • геометрические пропорции, или пропорции, которые иногда называются непрерывными, когда один из членов одного ряда обязательно повторяется в другом: Н1 : Н2 = Н2 : Н3 и т. д. Н2 является здесь средней пропорциональной величиной.

Существуют, таким образом, различные виды пропорциональных отношений, начиная от самых простых арифметических пропорций и кончая довольно сложными геометрическими пропорциями. Их очень много, но все они являются результатом подобия различных типов геометрических фигур, т. е. сочетания каких-то трех линейных величин этих фигур.

Немного особняком стоит геометрическая пропорция, которая получила название «золотого сечения». Золотое число Ф = 1,6180339..., которое называется еще «золотым сечением» или «золотой пропорцией», возникающей как результат решения геометрической задачи о делении отрезка в крайнем и среднем отношении, то есть делении отрезка на две неравные части таким образом, чтобы отношение большей части к меньшей равнялось бы отношению всего отрезка к большей части (математический анализ позволяет вычислить иррациональную величину Ф с помощью выражения (1 + √5)/2).

В эпоху итальянского Возрождения золотая пропорция возводится в ранг главного эстетического принципа. Леонардо да Винчи именует ее «Setio autea». Лука Пачели в 1509 г. пишет сочинение о золотой пропорции, названной им «божественной». По словам Иоанна Кеплера: «Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора, а другое – деление отрезка в крайнем и среднем отношении… Первое можно сравнить с мерой золота, а второе же больше напоминает драгоценный камень». В 1580 г. ученые обнаруживают проявление золотой пропорции в соотношении частей человеческого тела, животных, в эллинских храмах, ботанике, музыке (рис. 1.71).

Греки в своих скульптурах, отражающих совершенство творения, придерживались божественной пропорции. Места сочленения отдельных элементов скелета человека и животных являются точками деления целого в пропорции золотого сечения. Этот факт имеет и чисто механическое объяснение: оптимальным образом работает шарнирная пара, элементы которой находятся в пропорции золотого сечения. Пропорцией Ф определяется принцип строения живого организма, она является той универсальной мерой, позволяющей по установленным размерам одной известной части восстанавливать размеры следующей части и т. д.



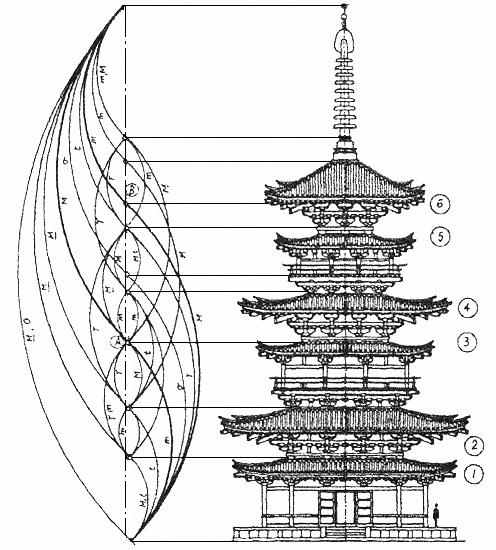
Рис. 1.71. Проявление золотой пропорции в строении храма
и строении человеческого тела

С помощью спирали золотого сечения представляется возможным решение таких задач, как квадратура круга и построение квадрата с периметром, равным длине окружности. Исследованию золотого сечения в средневековой науке посвящено сочинение «Liber abacci» знаменитого итальянского математика Леонардо из Пизы, который известен более под именем Фибоначчи (Fibonacci – сокращенное filius Bonacci, сын Боначчи). Эта книга, написанная в 1202 г., дошла до нас во втором своем варианте, который относится к 1228 г. Сообщаемый в «Liber abacci» материал поясняется на большом числе задач, в том числе и знаменитая задача о кроликах: «пара кроликов через месяц производит на свет другую пару, а потомство они дают со второго месяца после своего рождения. Итак, через месяц будет две пары, через два месяца – три пары, а через четыре месяца – пять, так как к паре, рожденной первой парой добавятся первые дети от второй пары…». Продолжая процесс, мы и получим количество пар кроликов по месяцам: 1, 1, 2, 3, 5, 8, 13, 21, 35, 56… – эти числа и представляют ряд, названный по имени автора задачи (ряд Фибоначчи7). Цифры этого ряда образуются как сумма двух предыдущих чисел. Их отношения 3/5, 5/8, 8/13 и т. д. близки к ряду золотого сечения. В образовании пропорции могут участвовать различные математические отношения, использующие ряды как целых, так и иррациональных чисел. Используются иррациональные отношения, и частности, образованные на числах ряда √5 (пентагональная система), √3 и √2.

Если говорить о натуральном ряде чисел, то можно представить себе такое рациональное их сочетание в единой модульной системе (расчленение тех же прямоугольников), которое строится на подобии их элементов и соотношения которых являются кратными (1:2, 1:3 и т. д.), т. е. основаны на натуральных числах. Иррациональные числа √2 или 1,414; √3 или 1,732; √5 или 2, 236, обычно никогда в чистом виде не используются.

Используются или отношения, образованные иррациональными числами, или сочетание целых чисел с иррациональными.

Графическое построение геометрических фигур, в которых имеет место сочетание целых чисел с иррациональными, производится довольно просто. Берется основание квадрата, потом его диагональ – соотношение диагонали квадрата с целым числом дает √2; потом диагональ этой фигуры, еще раз положенная в основание, – сочетание опять с единицей квадрата дает соотношение √3; следующая диагональ этого прямоугольника, опять превращенная в основание, в соотношении дает √5. Таким образом, полученные прямоугольники есть соотношение единицы √2, √3 , √4 и √5. Это сочетание, в свою очередь, образует отношение золотого сечения.

Дизайнеру необходимо не только знать принципы построения пропорций, но и уметь правильно использовать их для гармонизации формы предмета. Использование пропорциональных соотношений является очень сильным средством для получения целостной формы, так как создает твердую соразмерность отдельных линейных и объемных частей изделия. Но пропорциональность служит и решению главных, функциональных задач. Например, пропорции стола связаны с его функцией: обеденный стол или стол для переговоров целесообразнее делать квадратным, но для письменного стола, за которым сидит один человек, квадратная форма вряд ли целесообразна.

Выделяют два приема пропорционирования промышленных изделий: соподчинение и расчленение. Соподчинение используется тогда, когда к какому-то элементу пристраивается другой, который находится в смысле соразмерности в подчинении к этому основному элементу. Расчленение используется тогда, когда имеется какой-то объект (самый простой случай – прямоугольник) и эту основную форму или плоскость надо разбить на более мелкие элементы.

В дизайне основным является прием расчленения, потому что дизайнер обычно имеет дело сначала с общими габаритами вещи и уже внутри них ищет соотношение отдельных элементов между собой.

Пропорциональные отношения могут оказывать непосредственное влияние на композицию, так как соподчинение элементов формы во многом зависит от размерных отношений. Так, пропорции выражают связи формы и конструкции, т. е. обусловливают тектонику и характер объемно-пространственной структуры. С пропорциями связаны такие важнейшие качества, как статичность и динамичность формы, ее зрительная устойчивость. На пропорциональных отношениях могут строиться контраст и нюанс соотносимых величин, ритм и метрический повтор.

Правильно найденные пропорции способствуют не только достижению гармоничной формы, но и улучшению функциональных и конструктивных показателей изделия. Поэтому при проектировании технических объектов поиск системы пропорций необходимо вести уже на ранних этапах работы.