Введение в логистику
| Вид материала | Реферат |
СодержаниеP(x,y). Возьмем частные производные от P(x,y) |
- 1. введение в логистику, 531.6kb.
- Тренинга, 62.37kb.
- В россии строятся складские терминалы или единичные логистические центры, которые, 104.2kb.
- Джон Р. Хикс. "Стоимость и капитал", 4314.44kb.
- Введение глава психологизм как особенность характерологии в рассказах Всеволода Иванова, 12.47kb.
- Лабунец Ольга Юрьевна мытищи 2009 г. Оглавление Введение 3 Использование видеофильмов, 263.17kb.
- Анализ и планирование трудовых показателей Аудит и контроллинг персонала Введение, 12.45kb.
- Программа курса. План семинарских занятий Методические рекомендации Новосибирск 1999, 340.75kb.
- Учебной дисциплины (модуля) Наименование дисциплины (модуля) Введение в спецфилологию:, 83.08kb.
- 1. Целеполагание в процессе менеджмента Введение, 49.78kb.
Под распределительным центром (РЦ) понимается территориально обособленная закупочно-сбытовая организация, центрировано снабжающая торгующие предприятия товарами широкого потребления. Локальная территория, на которой находятся населенные пункты, торговая сеть которых обслуживается одним РЦ, носит название логистического полигона (ЛП).
Определение количества и оптимальной дислокации распределительных центров обычно требуют большого объема исходной информации, которая включает:
- перечень всей продукции и продуктовых миксов, хранимых и обрабатываемых на складе;
- дислокация основной массы потребителей, точек хранения, источников пополнения распределительных центров;
- спрос на каждую единицу продукции от определенной территориальной группы потребителей;
- транспортные тарифы (или издержки);
- время доставки, логистического цикла;
- затраты на складирование;
- затраты на закупку и себестоимость продукции и т.д.
Таким образом, для определения количества и оптимальной дислокации РЦ необходимо анализировать большое количество исходной информации, для чего требуются достаточно сложные экономико-математические методы и модели. Как правило. Эти задачи решаются на компьютерах с применением методов имитационного моделирования, операционного исчисления, теории графов и т.п. Рассмотрим некоторые алгоритмы оптимальной дислокации РЦ.
Предположим, что в рассматриваемой территориальной зоне (регионе, районе, городе) известны количество (К) потребителей продукции фирмы, их местоположение, объемы спроса на ГП (РК) в целом и по номенклатурным группа, характеристика транспортной сети и маршруты доставки. Экспертным методом определены количество (N) и месторасположение предполагаемых РЦ.
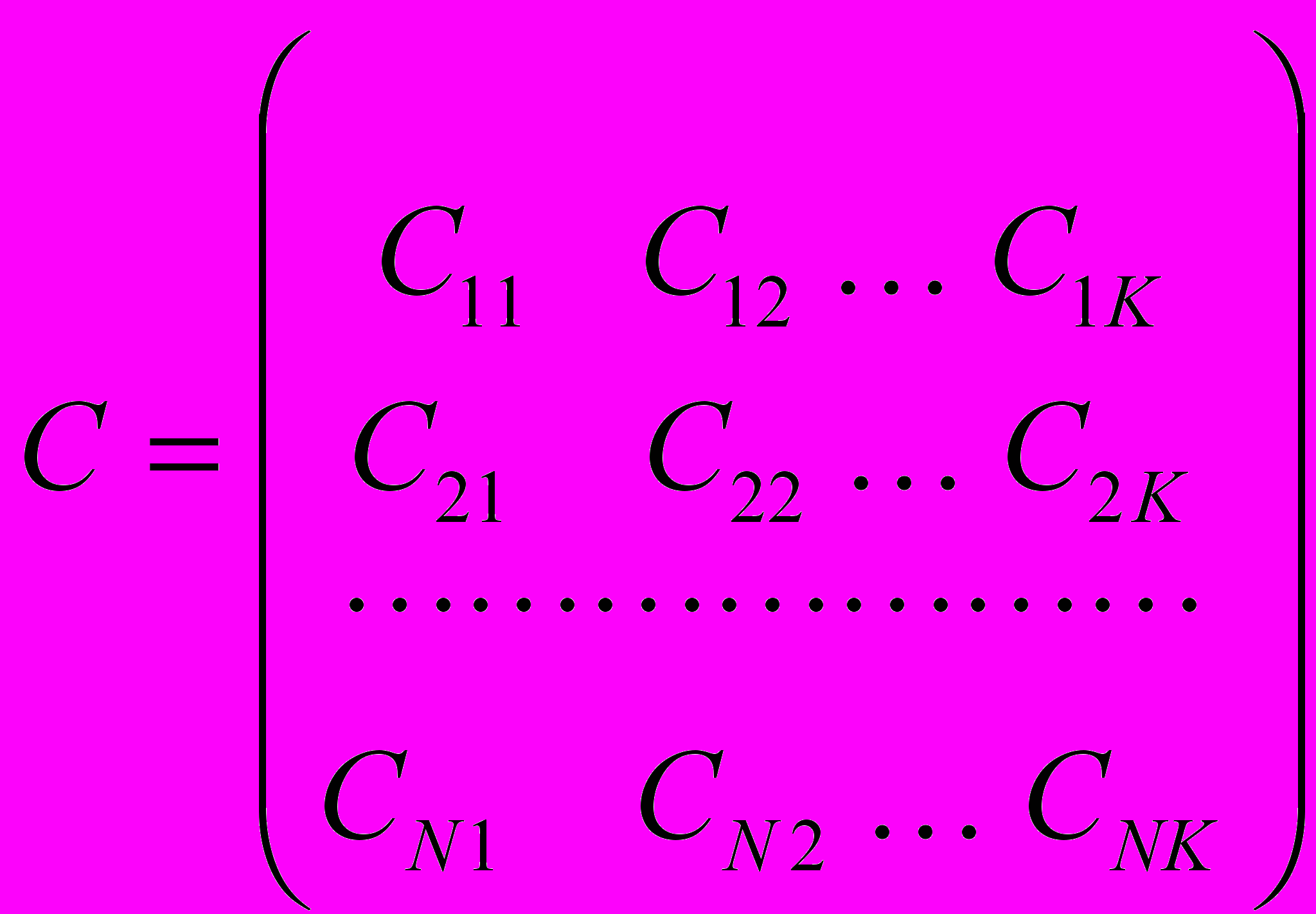
Известны также транспортно-складские расходы по доставке товаров от предполагаемых РЦ к потребителю в виде матрицы затрат:
Известны также годовая пропускная способность (годовые объемы реализации РЦ) (x1, x2, x3…xN), и условно постоянные логистические издержки каждого предполагаемого РЦ, не зависящие от объема реализации (b1,b2…bN).
Необходимо выбрать оптимальное количество РЦ и их место дислокации. Это и есть оптимизационная задача теории исследования операций.

В качестве элементов решения вводят матрицу предполагаемых перевозок:
Эти положительные числа должны удовлетворять следующим условиям:
- Суммарный годовой объем ГП, направляемый из каждого предполагаемого РЦ ко всем потребителям, должен быть равен годовой потребности каждого потребителя. Это дает нам n условий-равенств:
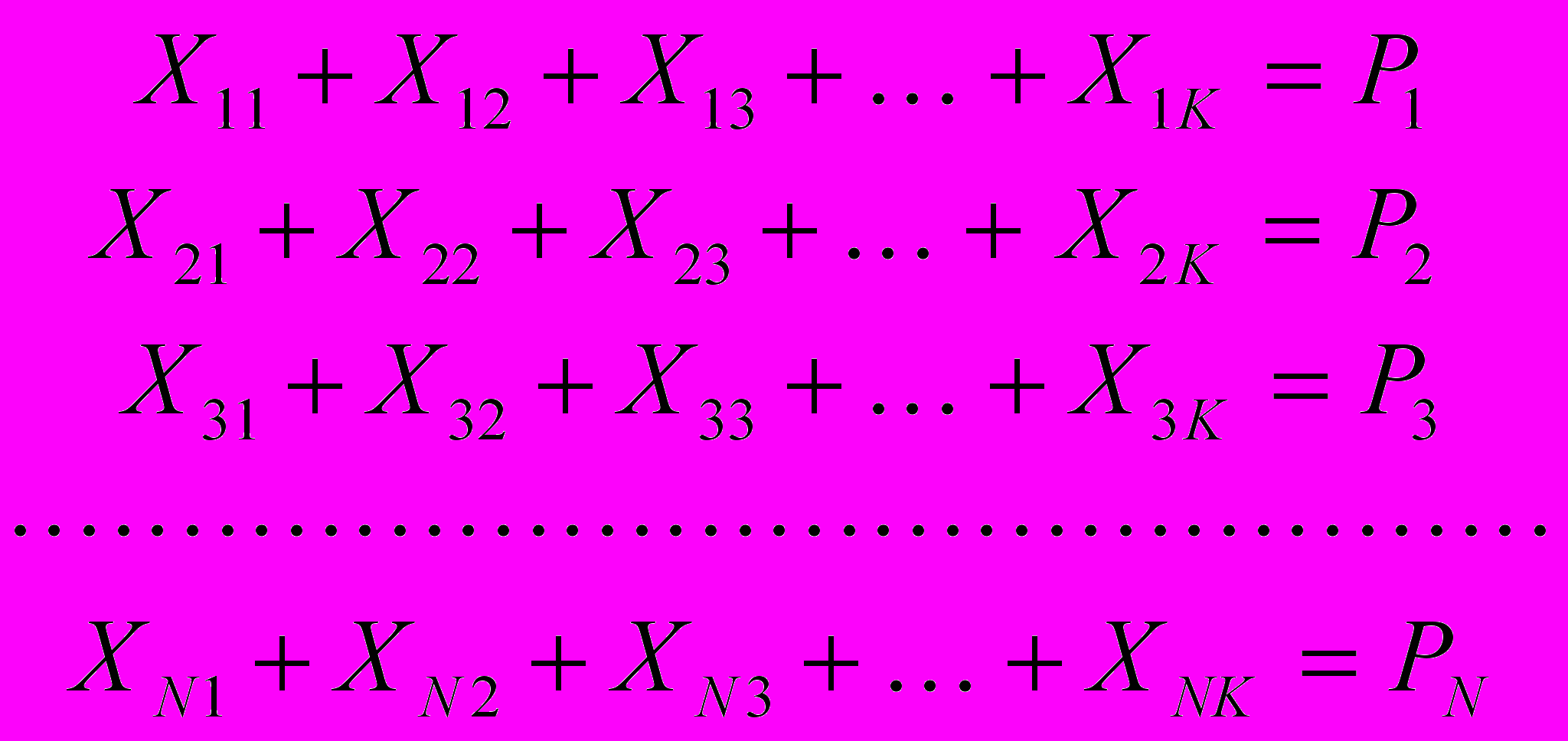

2
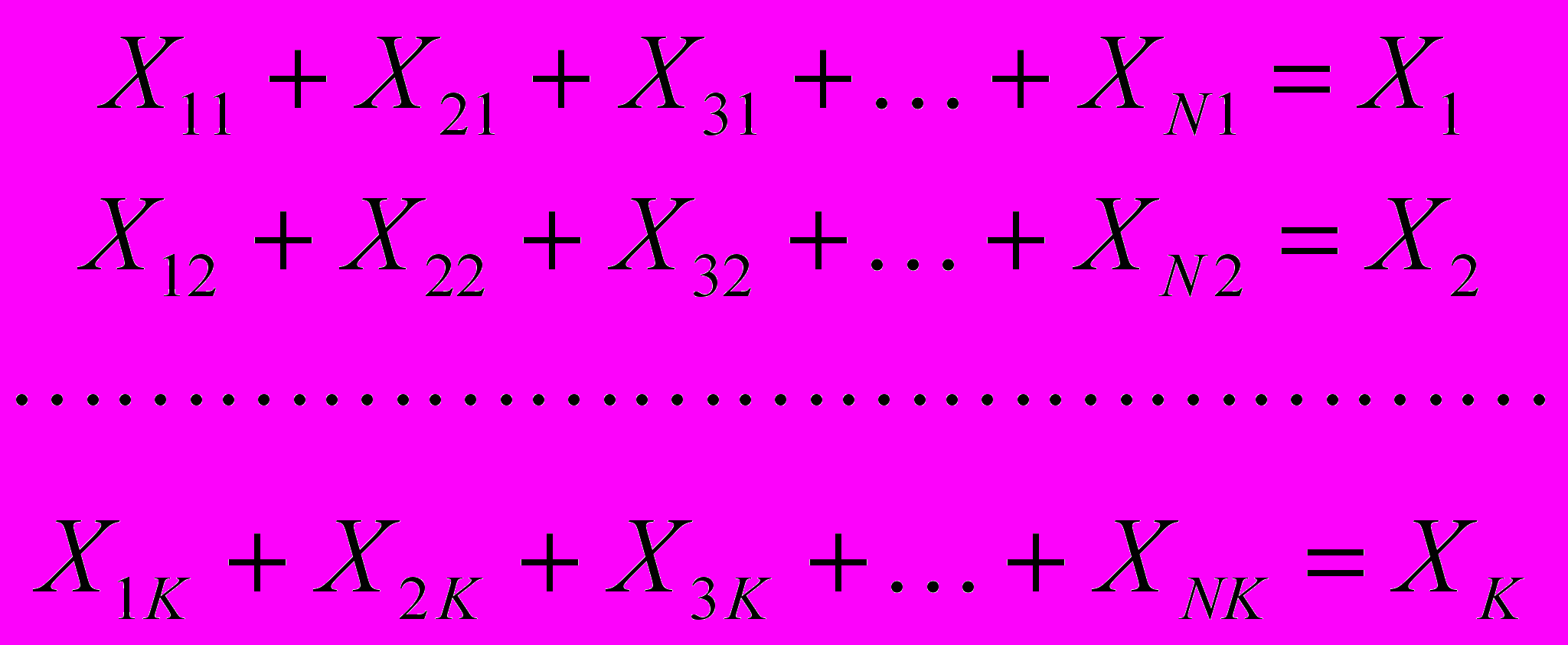
) Суммарный объем ГП, направляемый к каждому потребителю из всех предполагаемых РЦ, должен быть равен пропускной способности каждого РЦ. Это дает нам k условий-равенств:
- Неотрицательность переменных. При этом суммарные логистические издержки равнялись бы минимуму:
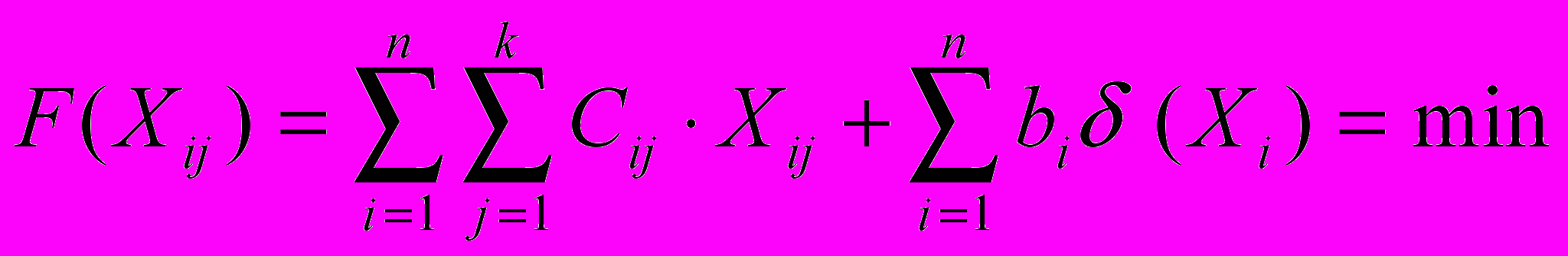
Величину δ (xi) определяют из условия:
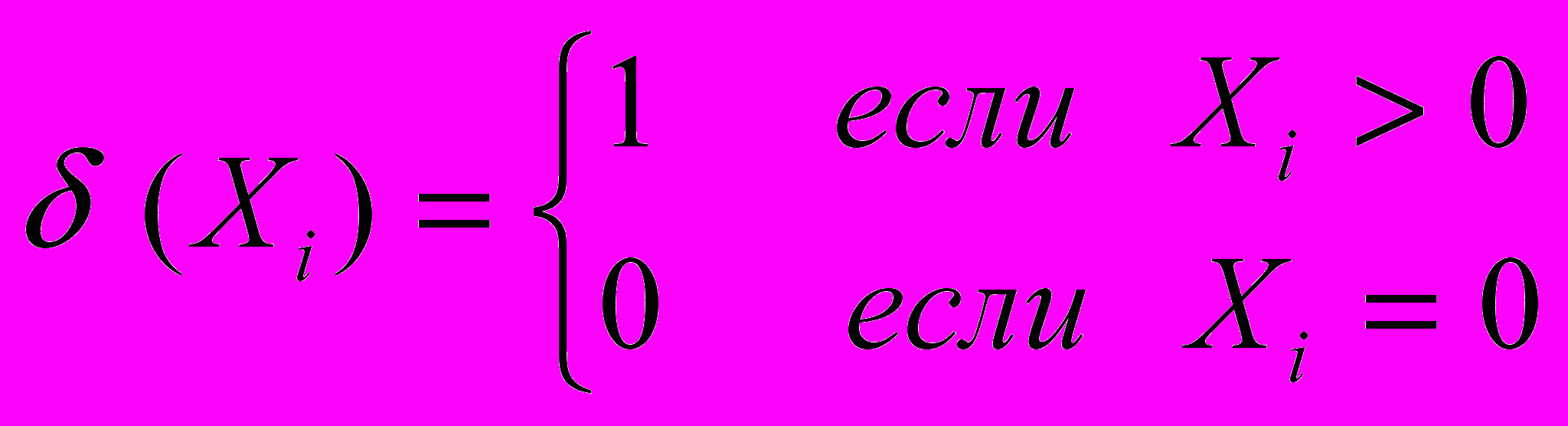
Оптимальная дислокация складов различного уровня может быть найдена с помощью следующего итерационного алгоритма.


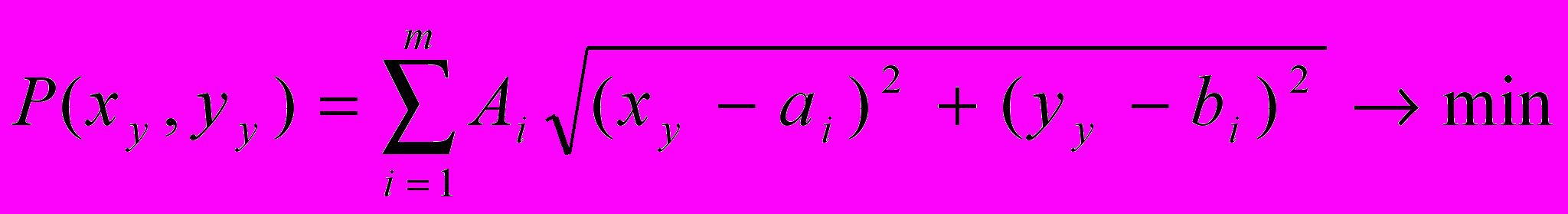
Сформулируем исходные данные следующим образом. Имеется m потребителей в некоторой территориальной зоне, заданных координатами (ai, bi), i=1, m. Каждый потребитель характеризуется объемом спроса на продукты Ai, i=1, m. Требуется определить координаты центра распределения (xy, yy) так, чтобы сумма расстояний от данных m точек с учетом спроса Ai до точки (xy, yy) была минимальной. Таким образом, на плоскости XOY необходимо найти точку (x, y) оптимальной дислокации, такую, что:
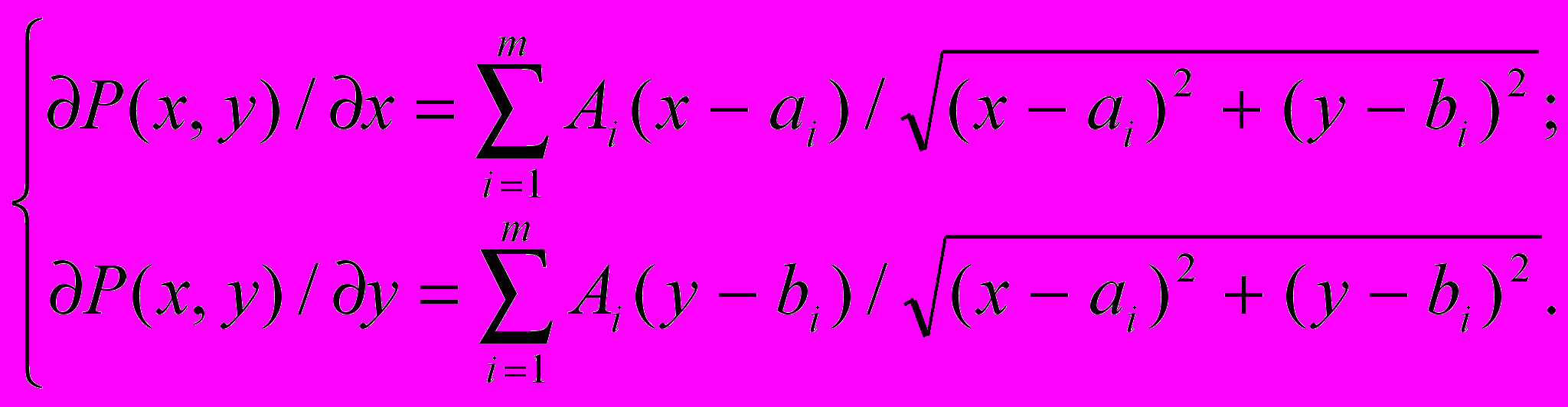
Опишем алгоритм нахождения минимума целевой функции P(x,y). Возьмем частные производные от P(x,y):
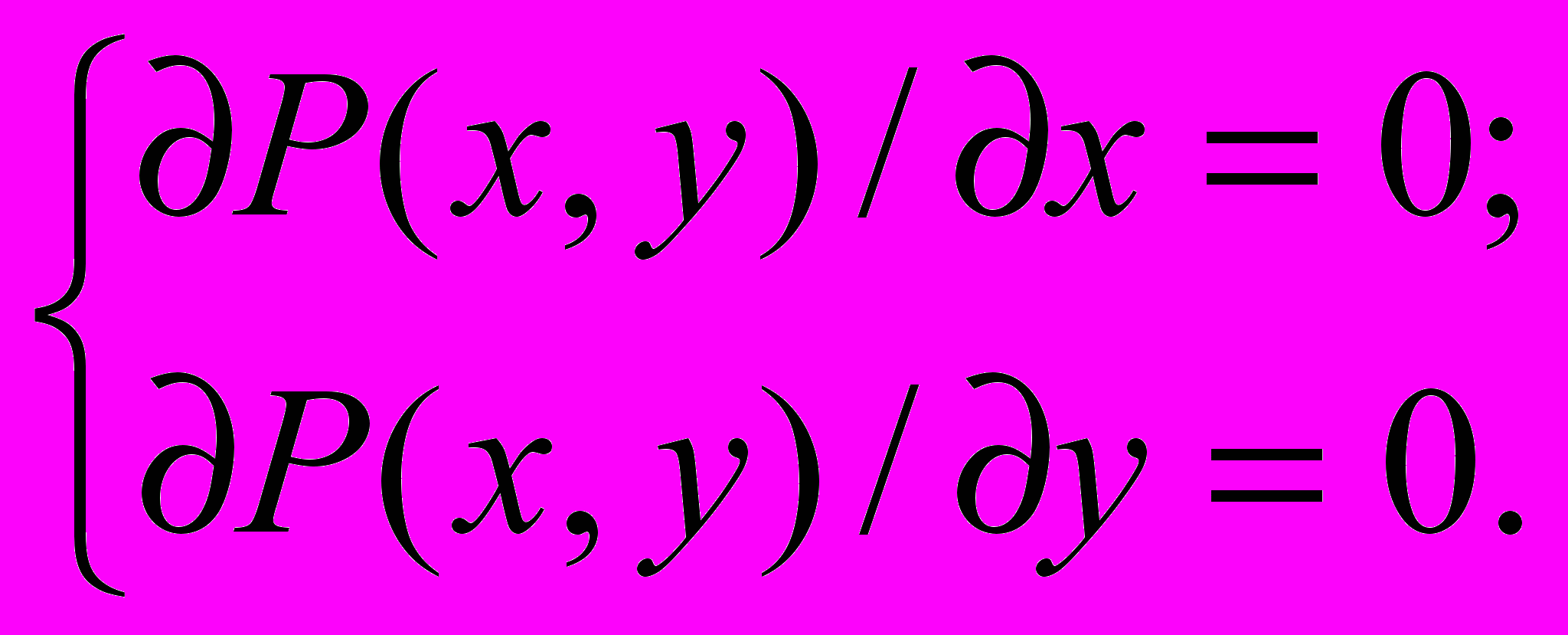
Из анализа известно, что для нахождения искомой точки (x,y) необходимо частные производные приравнять к нулю и решить систему уравнений вида:
Однако решение данной системы уравнений наталкивается на серьезные трудности ввиду ее нелинейности. Поэтому обычно используется итерационный метод решения.
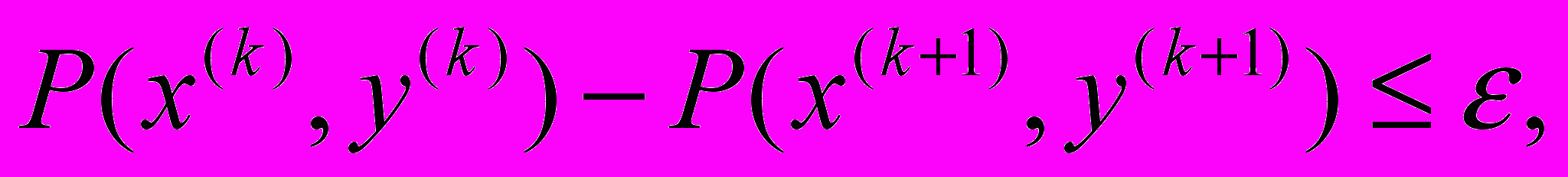
Первое приближение определяется по формуле:
г

де k - номер итерации, а ε - малое положительное число (заданная степень точности).
Функция P(x,y) выпукла снизу и имеет единственный экстремум, что в свою очередь, позволяет получить единственное оптимальное решение, используя приведенный выше алгоритм.
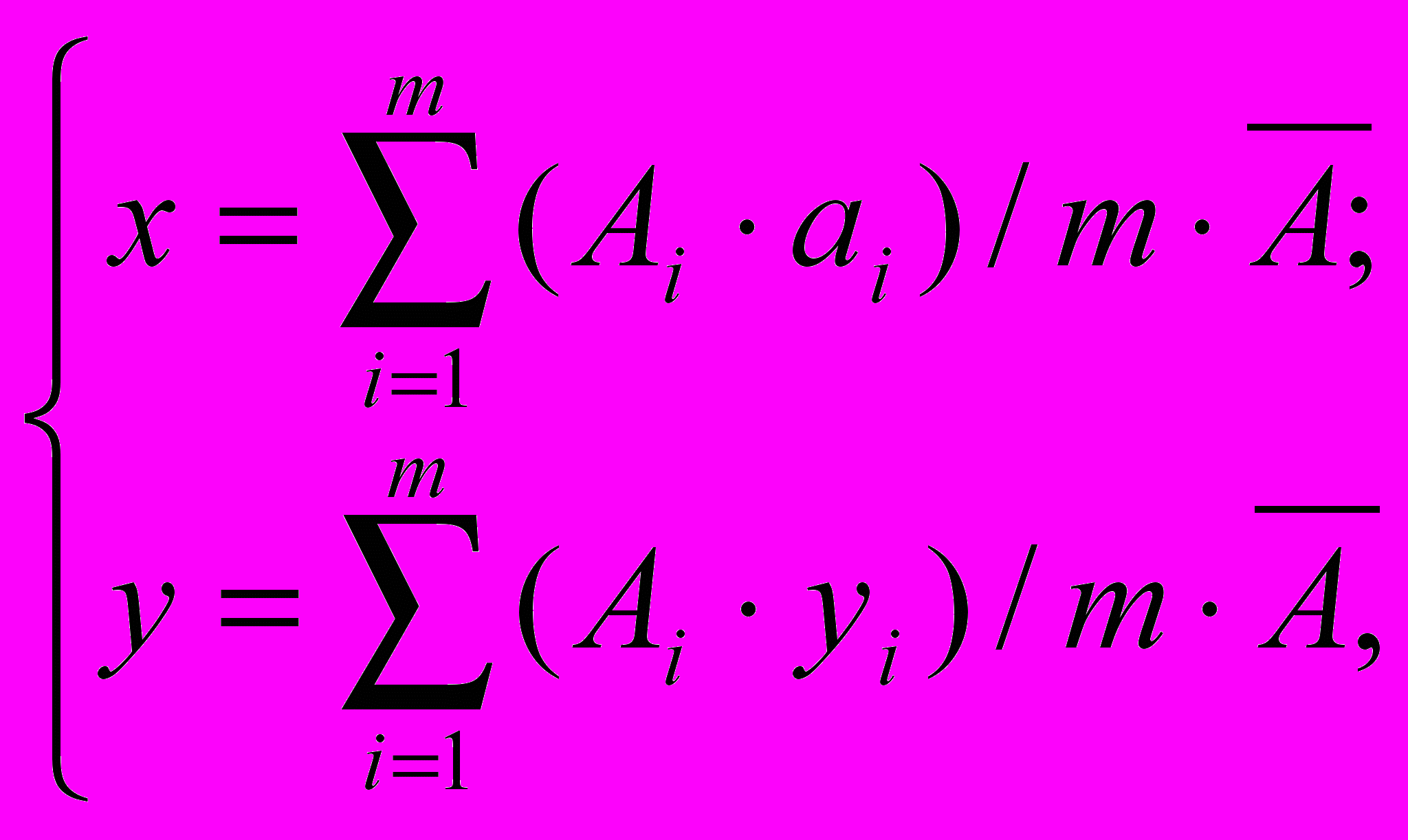
Можно показать, приближенное решение поставленной задачи достигается использованием следующих формул:
г
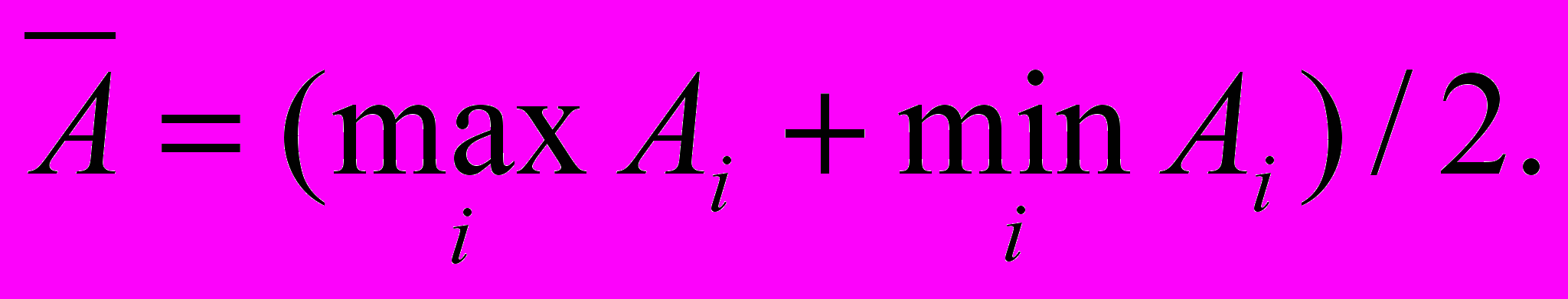
де Ā – средний спрос, определяемый по выражению:
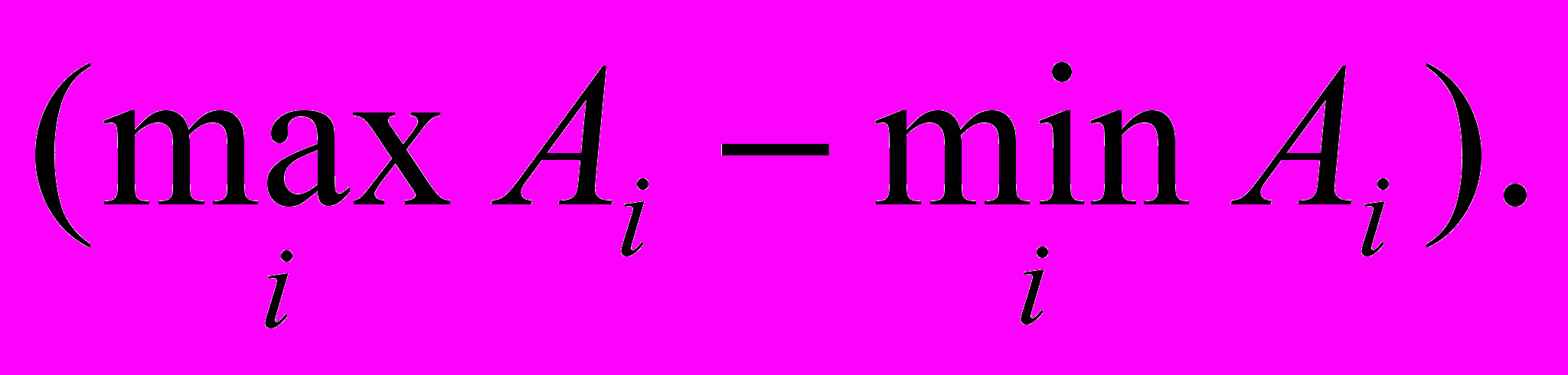
Очевидно, что при Ai=const, решение, получаемое с помощью приближенных формул, совпадает с оптимальным. Приближенное значение будет тем ближе к оптимальному, чем меньше разность:
Наукой и практикой выработаны различные методы решения задач обоих видов.
Задача выбора оптимального места расположения полным перебором и оценкой всех возможных вариантов размещения распределительных центров и выполняется на ЭВМ методом математического программирования.
Гораздо меньше трудоемки оптимальные методы определения места размещения распределительных центров. Суть метода рассмотрим на примере. Фирма, занимаясь реализацией продукции на рынках сбыта KА, KБ, KС, имеет постоянных поставщиков П1, П2, П3, П4, П5 в различных регионах. Увеличение объема продаж заставляет фирму поднять вопрос о строительстве нового распределительного центра, обеспечивающего продвижение товара на новые рынки и бесперебойное снабжение своих клиентов.
KА KС
● ●
KБ П5
● ●
П2 П3
● ●
П1 П4
● ●
Оптимальным расположением распределительного центра будет центр равновесия системы транспортных затрат, который определяется по формулам:
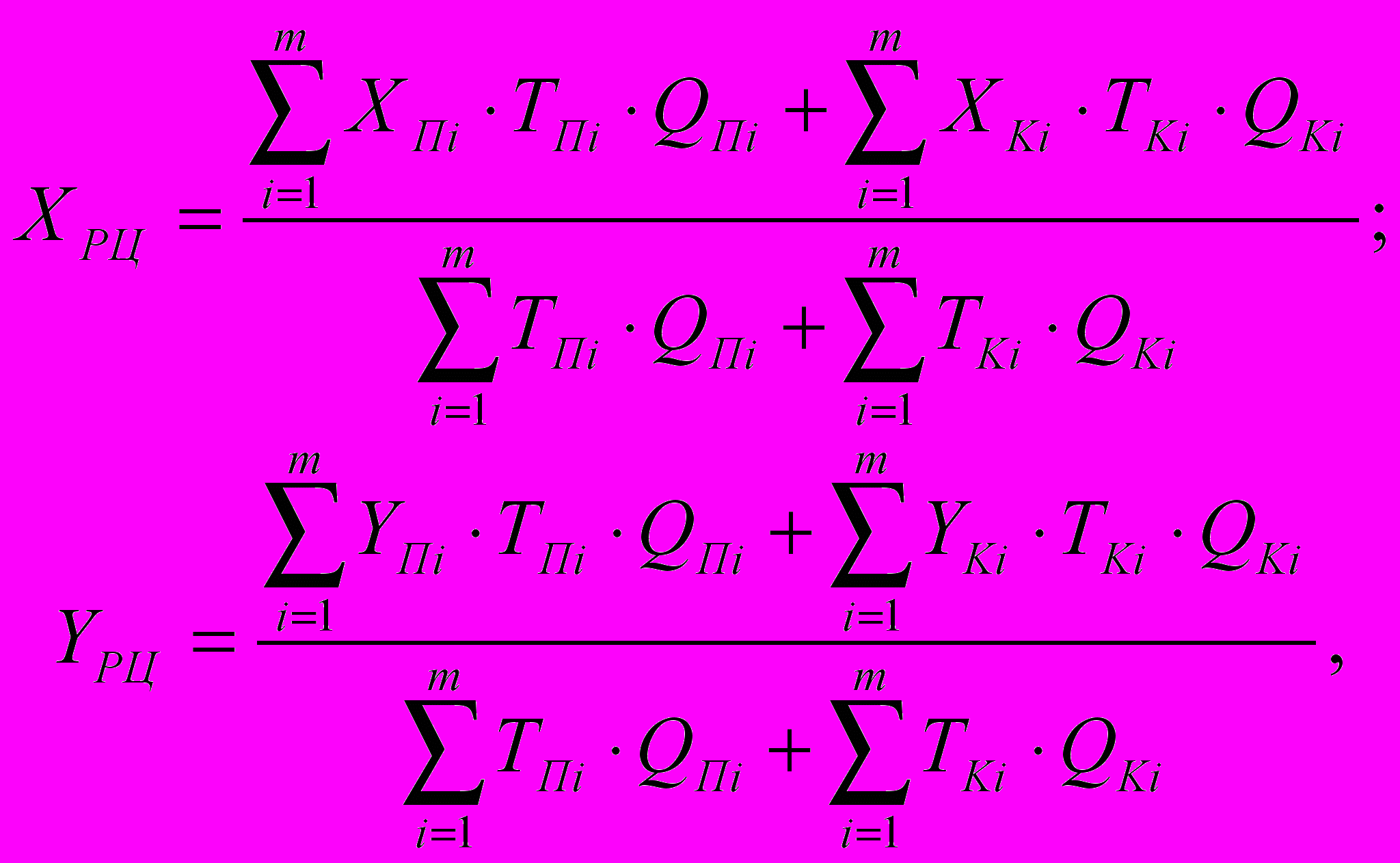
где XРЦ и YРЦ – абсцисса и ордината распределительного центра;
XПi и YПi – абсцисса и ордината месторасположения i–ого поставщика;
XKi и YKi – абсцисса и ордината i–ого клиента;
TПi – транспортный тариф для поставщика на перевозку груза, руб./т.км;
TKi – транспортный тариф для клиента на перевозку груза, руб./т.км;
QKi – вес (объем) груза, реализуемый i–м клиентом, т.;
QПi – вес (объем) груза, закупаемый у i-ого поставщика, т.
