Преподавание в вузе прогнозирование профессионально-методической подготовки будущего учителя

Вид материала

Задача

Содержание Об интегрированной системе компьютерного Покрытие задач: Мо – механический, одношаговый Показатели сложности ТЗ Экспертный метод Аналитические методы Критерии составления теста Общая схема функционирования интегрированной среды Из опыта подготовки учителя информатики младшей школы в красноярском государственном педагогическом университете Яковлева Т.А., Степанова И.Ю Сфера научных интересов – образовательная информатика. Основная работа: Изучаем Лого: Методическое пособие. – Красноярск, 1999 (в соавторстве с Яковлевой Т.Д.) Требования по дисциплинам информационного цикла Расширение требований к знаниям и умениям учителя начальных классов Информационные системы и компьютерные модели – Компьютерного практикума Шкерина Л.В. Изменение дидактики на основе Информационное обеспечение организационных задач. От лекции к телеконференции, от семинара к Интернет-дискуссии Информационные ресурсы для телекоммуникационного обучения ... Полное содержание

Подобный материал:

• Программа вступительного экзамена для поступления в магистратуру по профессиональнообразовательной, 85.07kb.
• Повышение качества подготовки учителя начальных классов в курсе по выбору «технологии, 78.76kb.
• Задачи практики: воспитание и закрепления интереса к профессии учителя физической культуры;, 415.17kb.
• В. П. Теория и практика методической подготовки педагогов профессионального обучения, 253.11kb.
• Планы семинарских занятий и методические указания по курсу для студентов всех специальностей, 426.37kb.
• Учебники по литературе и методические руководства Тематическое планирование и рабочая, 1484.97kb.
• Прогнозирование, 282.54kb.
• Интегрированный подход к профессионально-педагогической подготовке в вузе специалистов, 741.18kb.
• Электронное учебное пособие как средство формирования методической компетентности будущего, 41.11kb.
• План внутришкольного контроля научно-методической работы гоу сош №49 2011-2012 учебный, 244.94kb.

ПРЕПОДАВАНИЕ В ВУЗЕ

ПРОГНОЗИРОВАНИЕ ПРОФЕССИОНАЛЬНО-МЕТОДИЧЕСКОЙ ПОДГОТОВКИ БУДУЩЕГО УЧИТЕЛЯ

Тесленко В.И.


Тесленко Валентина Ивановна, зав. кафедрой методики преподавания физики, д-р пед. наук, профессор. В 1996 г. защитила докторскую диссертацию «Теоретико-методические основы диагностики и прогнозирования профессиональной подготовки учителя физики в педвузе». Имеет более 100 научных публикаций по проблеме вузовского образования.


Целью данной публикации является обобщение особенностей изу­чения подготовки студента с помощью оценочной диагностической ка­рты и разбор некоторых аспектов многофакторного прогнозирования профессионально-методической подготовки будущего учителя, роль которого в настоящее время возросла.

Методология многофакторного прогнозирования процесса подго­товки будущих учителей разработана недостаточно. Она требует решения ряда теоретических проблем, к которым относятся не только вопросы статистического и динамического прогноза, но и характер используемой статистической информации.

Задача статистического прогнозирования для каждого обуча­емого состоит в том, чтобы предсказать величину изучаемого показателя уровней подготовки будущих учителей в тече­ние определенного периода времени.

Предсказание результатов профессионально-методической под­готовки студента в будущем, сделанное на основе изучения его деятельности, – задача динамического прогнозирования.

Прогнозирование будет динамическим, если оно учитывает:

1. Общие закономерности изменения показателя качества сфо-рмированности профессионально-методических знаний, умений у студентов за данный промежуток времени. (Как идет процесс?).

2. Закономерности качественного изменения профессионально-методических знаний, умение у обучаемых. (Какова норма?).

3. Запаздывание в подготовке студентов.

Запаздывание, по сравнению с базовым стандартным уровнем, в подготовке будущих учителей можно определить по рядам динами­ки измерений, определенных показателем, и по самодиагностике ис­пытуемых. При этом учитываются следующие особенности:

1) проверенные количественные и качественные показатели должны охватывать определенный блок в подготовке студента (на­пример, специальный или методический блоки);

2) имеются теоретические обоснования по выделенным качест­венным и количественным показателям;

3) полученные показатели можно проверить, используя дру­гие методики.

Одним из способов изучения процесса профессиональной под­готовки является построение многофакторных моделей. Они бывают статические и динамические. Статические мо­дели можно построить по коэффициентам успешности или достижений студентов, относящихся к одному периоду времени, рассматриваемому как момент. Эти модели описывают закономерности, оп­ределяющие уровень профессиональной подготовки и разброс пока­зателей по различным видам деятельности студента в этот момент времени.

Как показывает анализ работ, в тракто­вке понятия «динамическая модель» нет единства. Одни считают, что динамическая модель – это та модель, которая построена по многофакторным динамическим рядам. Другие – если в ней учитыва­ются временные запаздывания влияний факторных признаков.

Для предвидения ра­звития процесса профессиональной подготовки каждого студента необходимо исследовать все динамические ряды достижений и успе­шности его обучения. Использование рядов динамики для диагно­стики и прогнозирования имеет целый ряд особенностей, яв­ляющихся следствием того, что они состоят из последовательных показателей, каждый из которых может дать необходимые сведения и представления о профессиональной подготовке студе­нта.

Решаемая проблема носит еще и социально-значимый ха­рактер, так как тесно связана с вопросами отчисления студе­нтов.

Отчисление – это крушение жизненных планов и ломка судеб большого числа молодых людей, которые при более профессиональном отношении к ним могли бы стать хорошими учителями. «Отсев – ес­тественный и необходимый процесс, но относиться к нему нужно осторожно, досконально изучая причины, приводящие молодых людей в тупиковые ситуации. Нужны серьезные профилактические меры» [1. С. 7]. Исследования, проведенные авторами [1], позволяют сделать нам определенные выводы относительно актуальности про­блемы диагностики и прогнозирования профессионально-методической подготовки будущего учителя. Данные показывают, что причине «неуспеваемость» отчисляется почти половина всех сту­дентов, выбывающих из педагогического университета. Примерно пятая часть отчисляется с мотивировкой в приказе «за пропуски занятий» и «за отрыв от университета». Как показали исследо­вания [1], наиболее сильными факторами, влияющими на отсев, студенты считают «неумение организовать самостоятельную работу», «отсутствие интереса к профессии учителя» и «плохую школьную подготовку». Анализ высказываний студентов и препо­давателей по поводу мер, способных уменьшить отсев, показал, что усиление профессиональной направленности учебной деятельности студентов будет способствовать сокращению отсева. Определенные надежды респонденты возлагают на дифференцированное обучение и усиление индивидуальной работы со студентами. На необходимость улучшить качество преподавания указали 46% студентов.

Приведенные выше данные еще раз подчеркивают актуальность проблемы диагностики и про­гнозирования профессионально-методической подготовки будущего учителя.

Следовательно, процесс диагностики и прогнозирования про­фессиональной подготовки студента преследует несколько целей:

1) предвидеть результаты и вовремя корректировать учебную деятельность будущего учителя;

2) проектировать заранее развитие личности студента;

3) развивать у студента прогностические способности и уме­ние предвидеть результаты своих действий и деятельности учащи­хся.

«Практика убедительно показывает, что способности и уме­ния, необходимые для предвосхищения будущего точного педагоги­ческого расчета, могут успешно формироваться как в процессе ву­зовской подготовки будущих педагогов, так и в ходе практической деятельности учителя» [2. С. 6].

Реализация этих целей предполагает развитие денных умений в деятельности, моделирующей педагогическую деятельность учи­теля, на основе активного и целенаправленного практического ис­пользования опыта, представленного в знаниях и навыках. Любая цель формируется на основе сложного двухпланового отражения действительности. Во внутреннем плане она является отражением потребностей субъекта, а во внешнем – реальных возможностей объективного мира [3].

Как отмечалось выше, в современных условиях, невозможно

составить полного и правильного представления о процессе прогно­зирования профессиональной подготовки студента, если не принять во внимание, что выявление закономерностей вузовского педагоги­ческого процесса идет через структурный и функциональный анализ деятельности. Системный подход становится в настоящее время ос­новным методом исследования. Особенно важно, что он позволяет ставить различные проблемы, возникающие при подготовке студентов в педвузе, и находить пути их решения.

В рамках данного подхода рассмотрим методы прогнозирования профессионально-методической подготовки будущего учителя. Сле­дует заметить, что в основе любого метода прогнозирования лежит идея экстраполяции – продления динамического ряда показателей успешности обучения студента за пределы исследованных периодов. Каждая экстраполяция обязательно основывается на предположе­нии, что закономерность развития, найденная внутри динамического рядя, сохранится и вне этого ряда в дальнейшем развитии.

Остановимся на содержании методов, которые можно применить для прогнозирования профессионально-методической подготовки сту­дента.

Первый, наиболее простой и наглядный, на наш взгляд, – это метод выявления основной тенденции. В основе этого метода лежит предположение, что рассматриваемый ряд динамики имеет некоторую закономерность, которая может быть выявлена кривой, проведенной через конкретные точки этого ряда. Этот тип методов носит назва­ние «аналитического выравнивания».

Необходимо заметить, что основой для выбора кривой, описы­вающей тенденцию, является всесторонний теоретический анализ су­щности профессионального обучения будущего учителя. В аналитическом выравнивании динамических рядов время рассматривается как независимая переменная, а уровни ряда выступают как функции этой независимой переменной.

Выравнивать ряды динамики можно с помощью конечных разно­стей метода наименьших квадратов. Как показывают исследования, метод выравнивания динамических рядов с помощью конечных разностей по сравнению с методом наименьших квадратов требует меньшего количества различных вычислении.

С помощью метода конечных разностей находят ту же линию, что и методом наименьших квадратов, так как параметры уравне­ний, полученные обоими методами, равны.

Покажем на примерах использование метода выявления основ­ной тенденции для прогнозирования профессионально-методическойподготовки студентов.

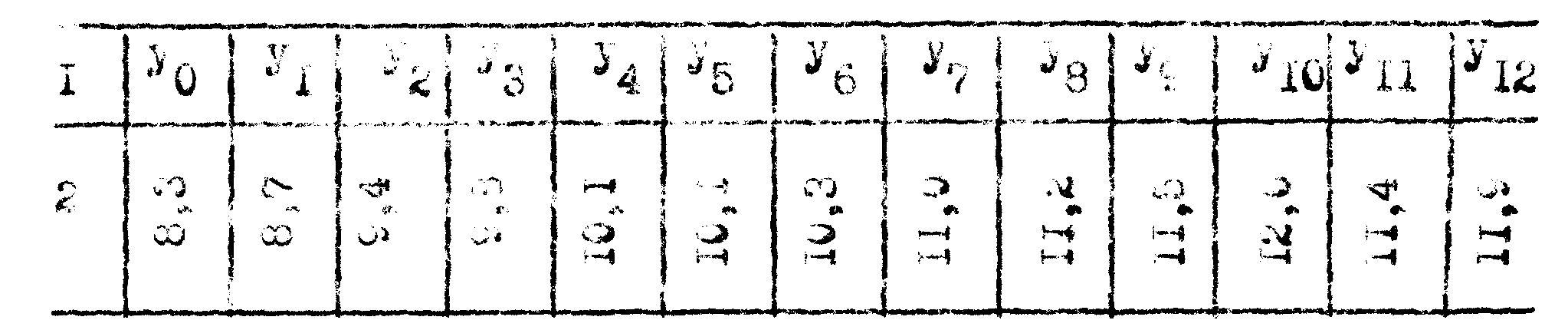
Фиксируя уровень сформированности у студента умения обу­чать учащихся самостоятельной работе с учебной литературой по физике, мы получим динамический ряд:



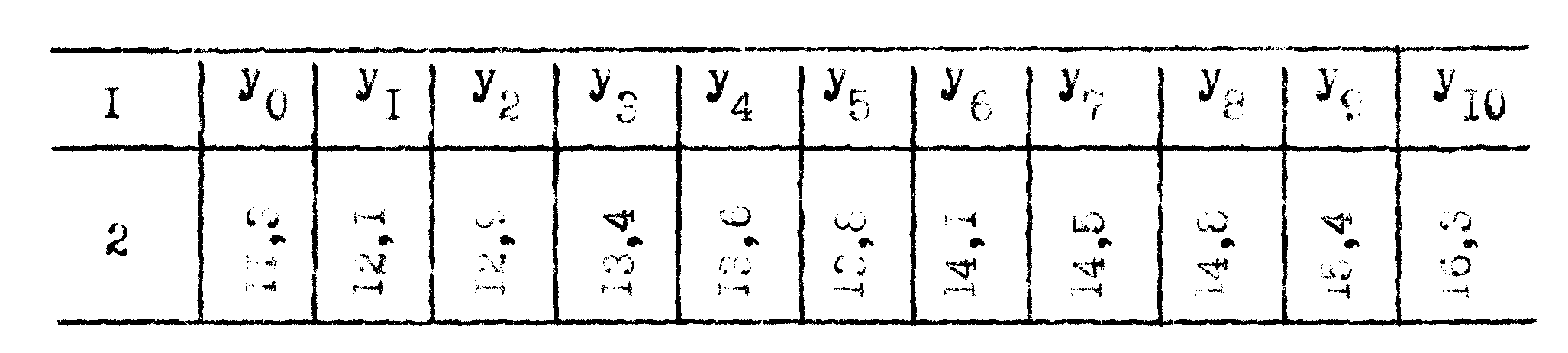
где: 1 – обозначение уровня сформированности умения;

2 – уровень сформированности в баллах. Найдем закономерность изменения уровня сформированности данного умения.

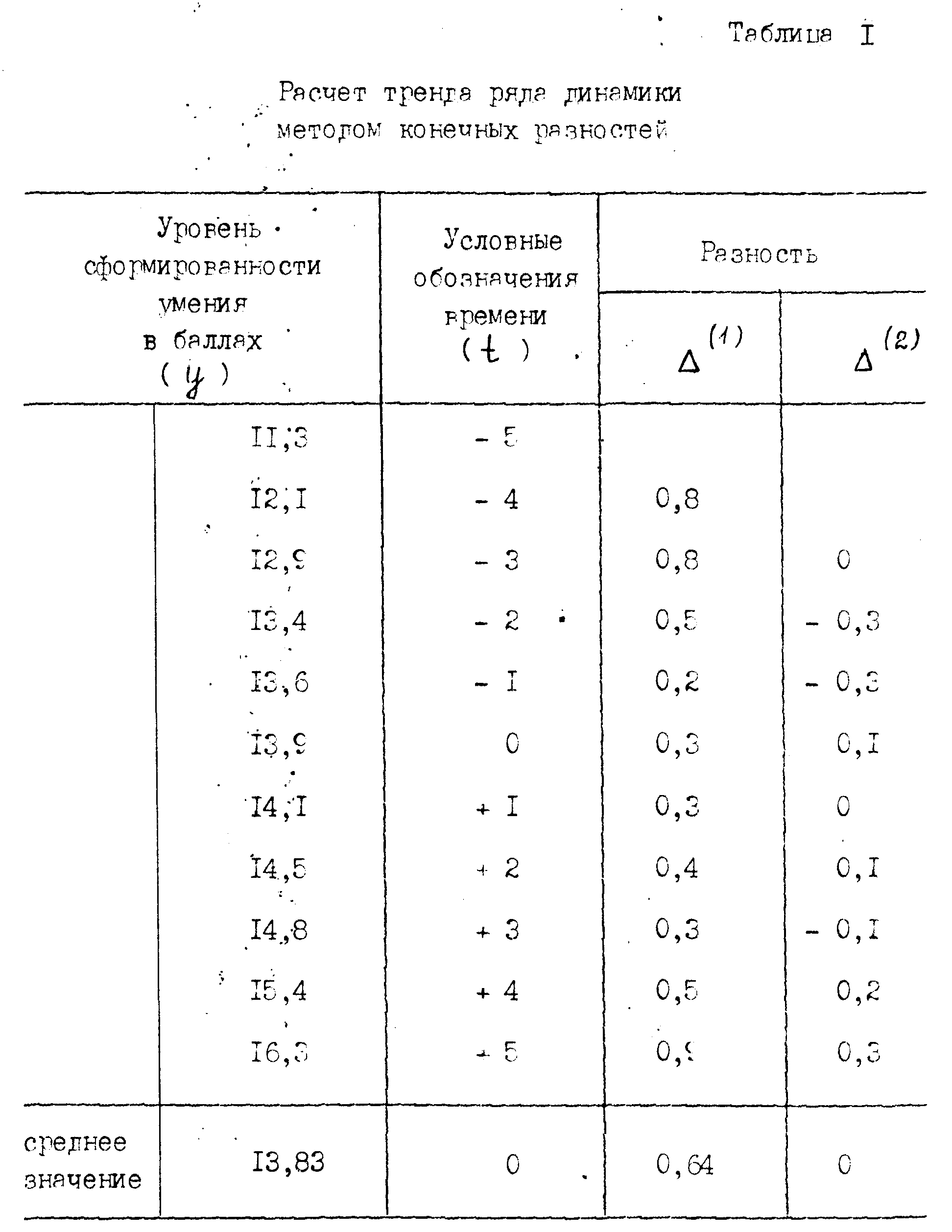
Расчеты приведены в таблице 1. Первые разности вычислены по формуле:



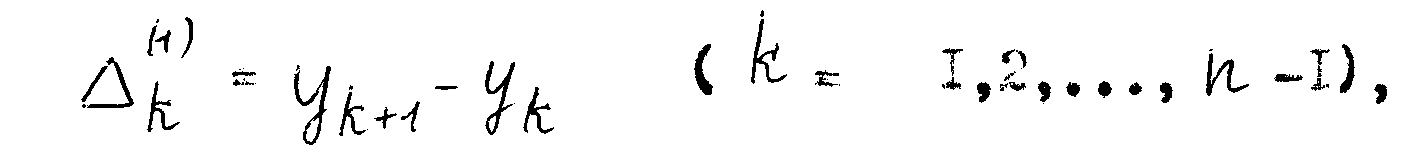
вторые разности:



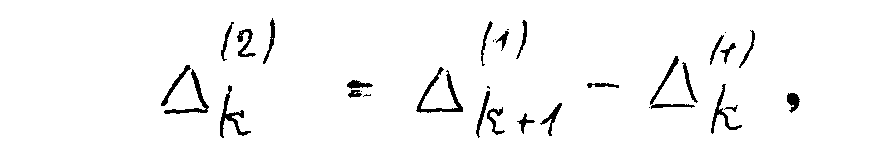
третьи разности:



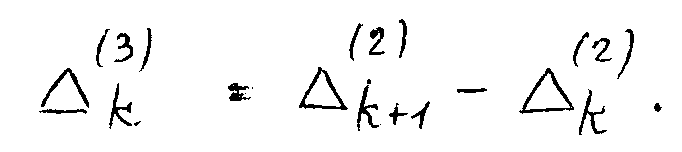
Данные таблицы 1 показывают, что средняя арифметическая вторых разностей равна 0. Следовательно, тенденция данного ря­да динамики – прямая линия. Учитывая, что ў= 13,83 (среднее значение уровня), а (∆) = 0,64, ее можно записать в виде ура­внения:




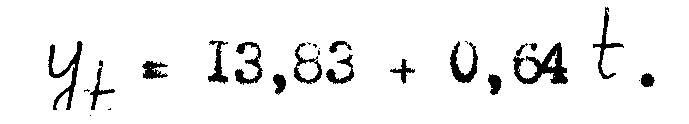
На основании полученного уравнения можно спрогнозировать, что уровень сформированности данного умения с течением времени постепенно повышается, но его изменение во времени будет проис­ходить медленно, поэтому на данного студента следует обратить особое внимание.

Найдем закономерность изменения уровня сформированности профессионально-методических умений у студента во время обу­чающей педагогической практики в школе (уровень сформированности проверялся с помощью тестов).

М
ы получим следующий динамический ряд:





Средняя арифметическая третьих разностей ра­вна 0, следовательно, основную тенденцию изменения уровня сформированности профессионально-методических умений на первой педагогической практике можно представить параболой второго порядка (расчеты в таблице 2), где





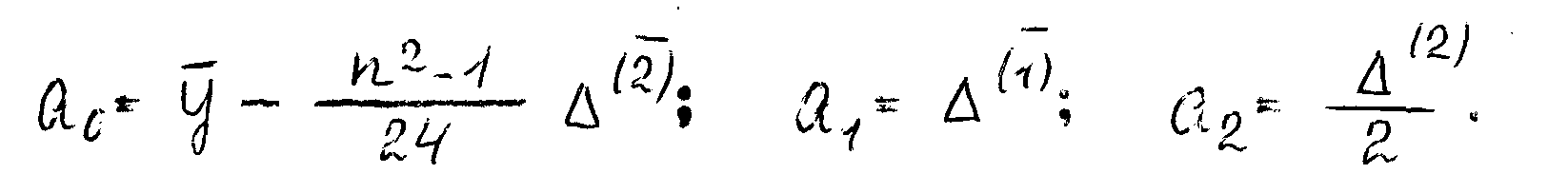
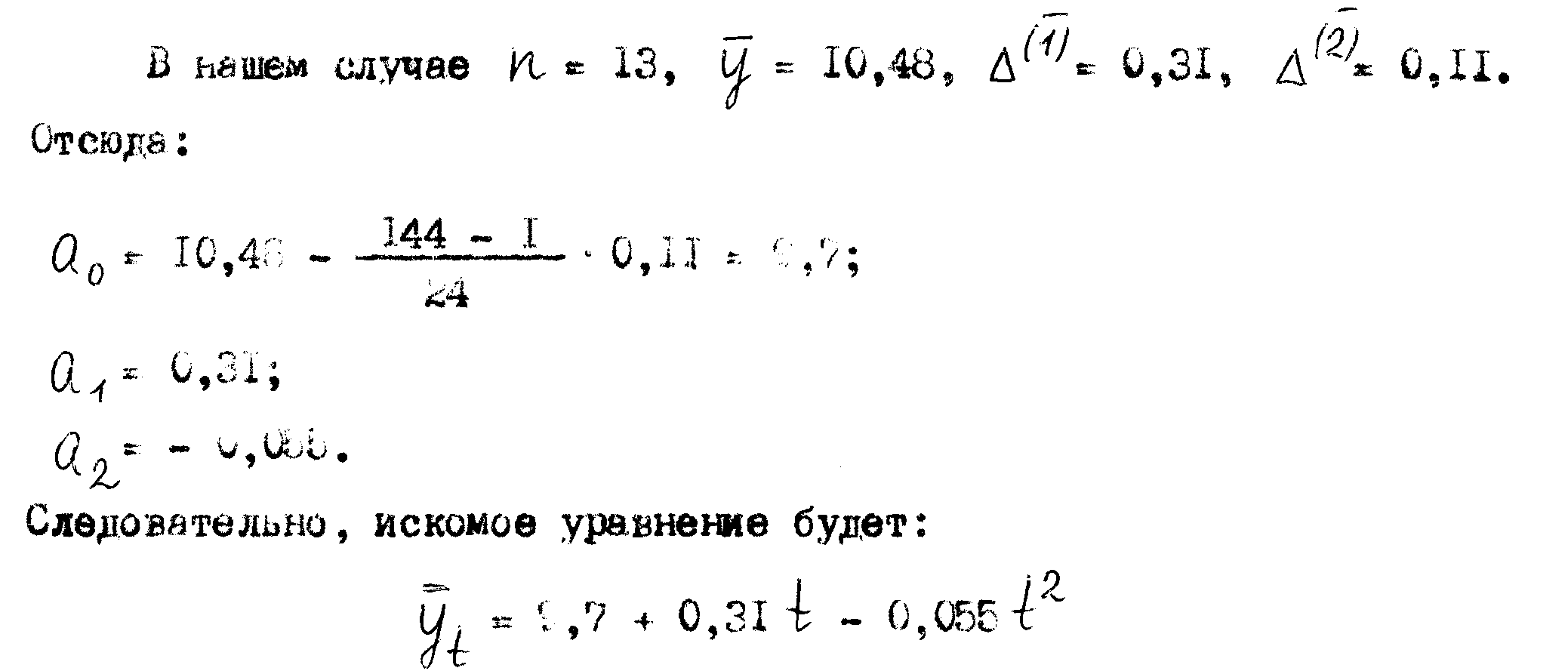
и на основании его можно сделать прогнозирование относительно данного студента.

Такие динамические ряды можно получить по каждому учебному предмету различных циклов, используя специальную систему заданий и педагогические тесты. На рис. 1 показан сетевой график получения динамических рядов, который может использоваться для составления специальной профессиональной карточки студента по­сле поступления в педагогический вуз.




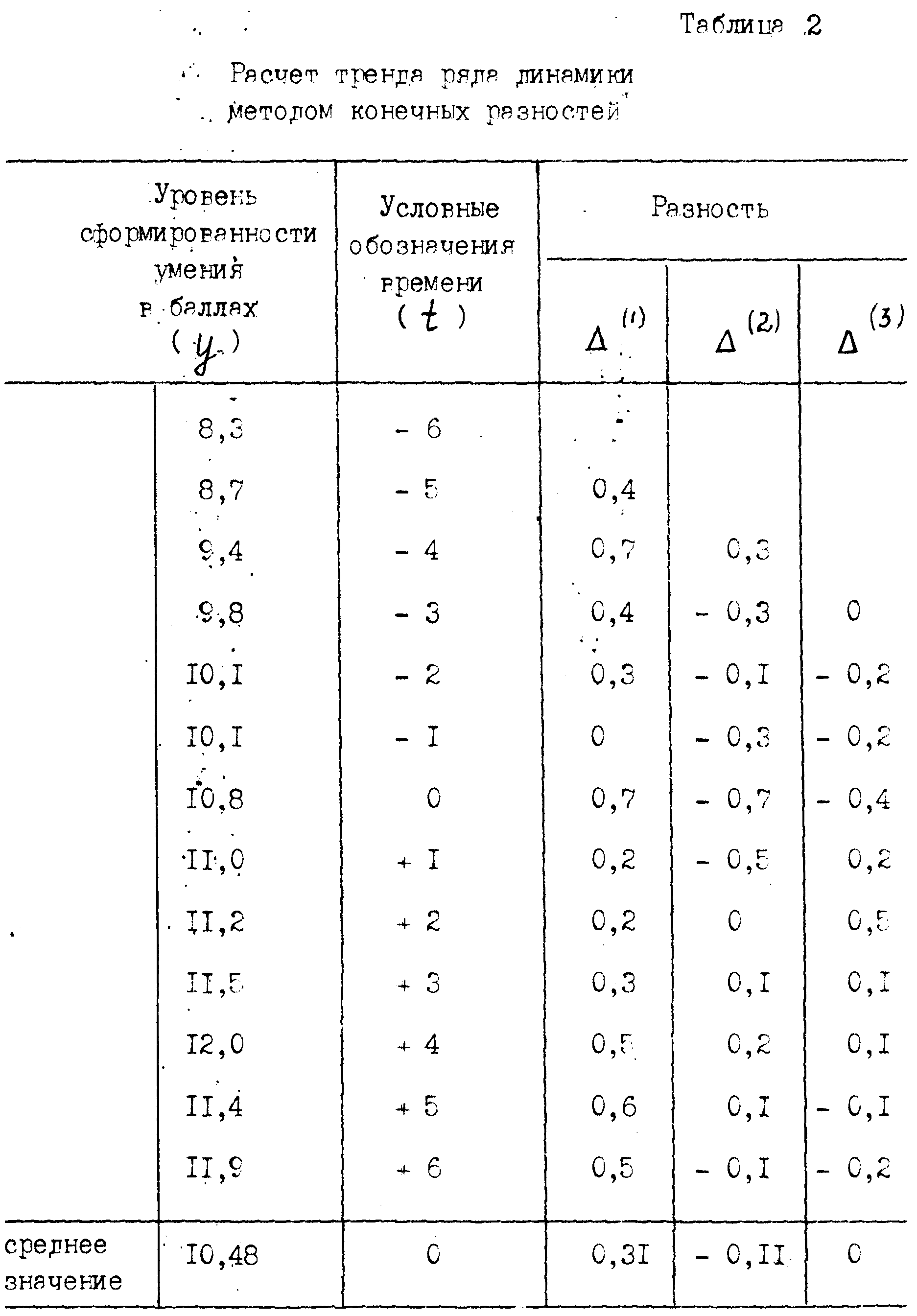
Такие карты должны быть заведены на каждого студента.

По горизонтали выделены блоки: общекультурный, психолого-педагогический, специальный, методический и педагогической практики. По вертикали – 4 уровня профессионально-методиче­ской подготовки. Четвертый уровень под­готовки (специальный базовый) должен быть сформирован у выпускника педвуза перед началом его самостоя­тельной педагогической деятельности.

Как показывает практика, при решении различного рода за­дач диагностики и прогнозирования профессионально-методической подготовки приходится рассматривать не один динамический ряд, а параллельно несколько рядов с целью изучения динамики неско­льких показателей. В этих случаях колебания уровней динамики взаимообусловлены.

При рассмотрении и изучении такого рода рядов динамики возникает необходимость установить зависимость между колебани­ями уровней различных рядов, измерить тесноту этой зависимости. Такие задачи решаются обычно корреляционным и регрессивным ана­лизами.

Метод корреляции долгое время не находил широкого приме­нения при изучении взаимосвязей рядов динамики из-за от­сутствия технических средств счета. И только появление электронно-вычислительной техники сделало возможным проводить корреля­ционный анализ параллельных динамических рядов, строить многофакторные корреляционные модели, решать корреляционные урав­нения с десятками параметров.




Условные обозначения:

0 – готовность студента до обучения в вузе;

I – информационный уровень;

II – репродуктивный уровень;

III – продуктивный уровень;

IV – базовый уровень;

□ – применяемая система заданий и тестов;

—— – прямая связь;

- - - – желательная связь;

ОКБ – общекультурный блок;

ППБ – психолого-педагогический блок;

СБ – специальный блок;

МБ – методический блок;

ПП – педагогическая практика.

Одни предлагают коррелировать не сами уровни рядов динамики, а отклонения от тренда. Другие считают, что лучше коррелировать разности уровней каждого ряда. Причем если уровни выровнены по прямой, то коррелируют первые разности, если по параболе второго порядка – вторые разности, если по параболе n-го порядка - n-е разности.

На наш взгляд, методологически наиболее правомерным явля­ется способ коррелирования отклонений от основной тенденции. Коэффициент корреляции при этом характеризует, на сколько коле­бания уровней одного ряда динамики вызывают колебания уровней другого ряда.

Хотелось бы сделать общее замечание. Приме­нение метода корреляции при изучении рядов динамики открывает возможности для их всестороннего исследования, для отыскания связей, для количественной характеристики тесноты этих связей. Однако математические формулы нельзя рассматривать как ключ к проникновению в существо связей. Все приемы статистического ис­следования долины применяться только после всестороннего изуче­ния их логической основы наряду с установлением факторов, за­кономерностей, связей,

Проиллюстрируем на конкретных примерах, как можно прово­дить прогнозирование профессионально-методической подготовки студентов, используя корреляционный и регрессионный анализы. (Это будет уже второе направление).

Допустим, мы измерили у каждого студента определенной группы уровень подготовки по предметам методического цикла и успешность их педагогической деятельности в школе. Получили два ряда динамики. Первый ряд:

x1, x2, x3, … , x_n,

где x_i – уровень подготовки i-го студента по предметам методического цикла; i – изменяется от I до n;

n – количество студентов.

Второй динамический ряд:

y1, y2, y3, … , y_n,

где y_i – успешность педагогической деятельности i-го студента на педагогической практике;

i – изменяется от i до n ;

n – количество студентов.

Опишем связь между этими рядами динамики в общем виде и спрогнозируем подготовку каждого i-го студента в данной со­вокупности измерений.

Наиболее просто представить связь в виде таблицы, в кото­рую занесены пары значений (x₁, y₁); (x₂, y₂);…; (x_n, y_n), соответствующие измерения, относящиеся к отдельному студенту. Однако более информационной формой для нашего случая является так называемая диаграмма рассеивания – график в коор­динатах x,y, на котором откладываются точки (x_i;y_i). Возможные типы таких диаграмм изображены на рис. 2.

Если корреляционная связь идеальна, в том смысле, что меж­ду x и y с высокой степенью вероятности существует линей­ная зависимость, а случайное рассеяние обеих величин пренебре­жимо мало, то на диаграмме связь изобразится в виде прямой ли­нии.



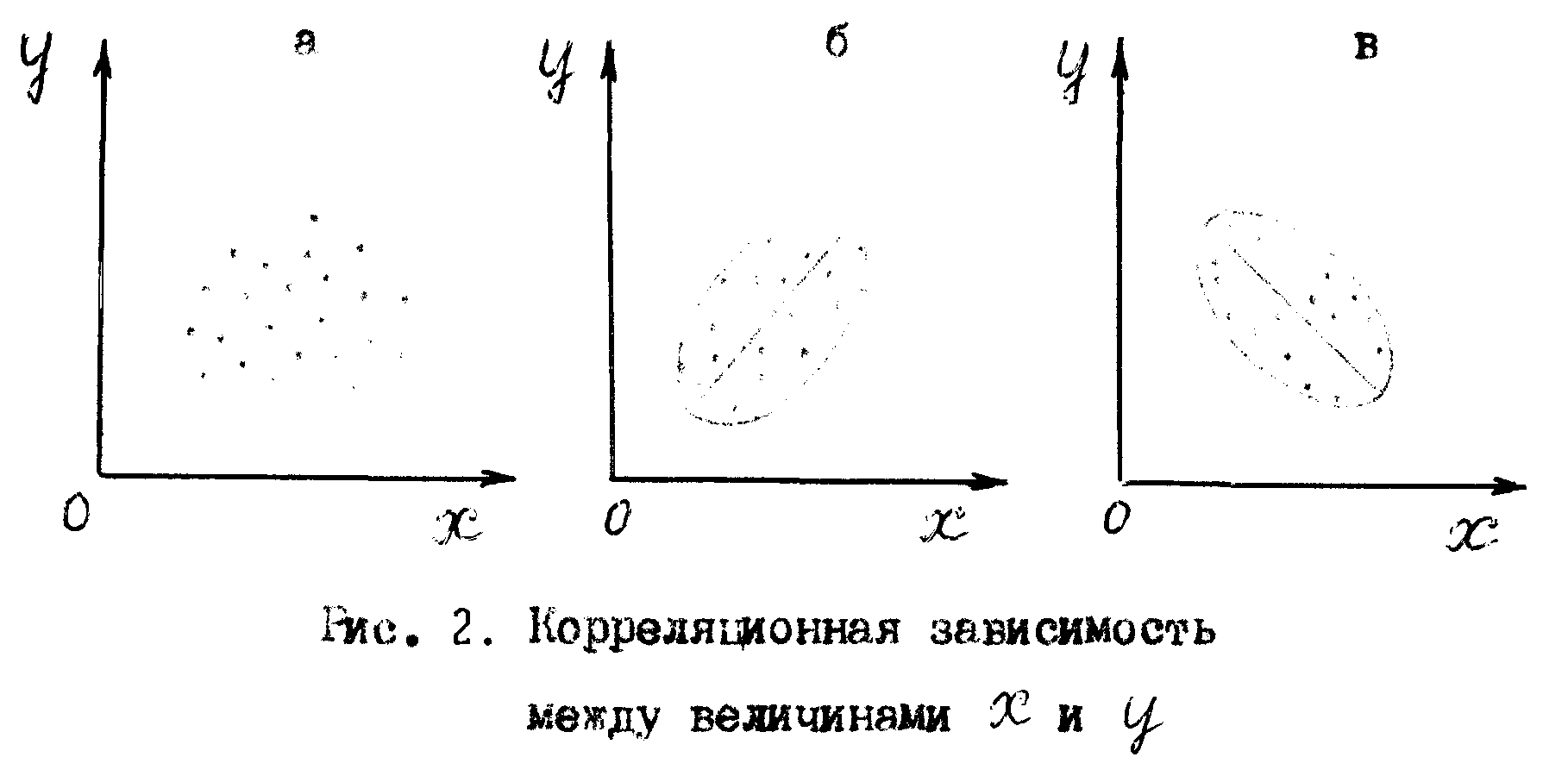
Поскольку случайное рассеяние всегда имеет место, точки будут располагаться на графике в некоторой конечной области, имеющей форму эллипса (б, в). Если связь отсутствует или не является линейной, разброс точек на диаграмме рассеивания бу­дет иметь вид хаотической области, близкой к кругу (а).

Графическое представление корреляции наглядно, однако это только качественная оценка. Поэтому она дополняется статистиче­скими расчетами, которые позволяют оценить силу связи количест­венно.

Покажем это на примере. Пусть мы построили и получили та­кую диаграмму рассеивания, как показано на рис. 4. На рис. 4 выделены границы некоторого облака.

Допустим, мы хотим что-либо сказать о студенте Иванове и сделать определенное относительно его предсказание. На диаграм­ме можно увидеть графический образ Иванова. Что это дает препо­давателю?

Найдем центр тяжести этого облака, а для чего определим средние значения x и y .



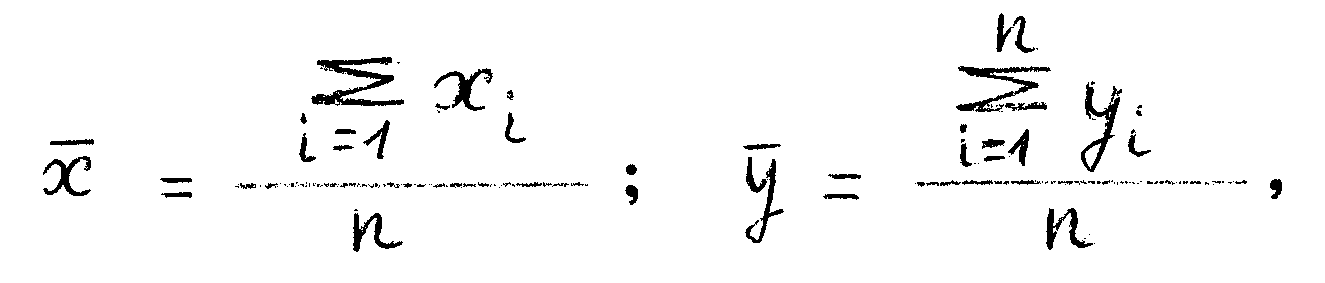
где n – количество студентов. Теперь разделим наше облако на 4 части (I, II, III, IV):



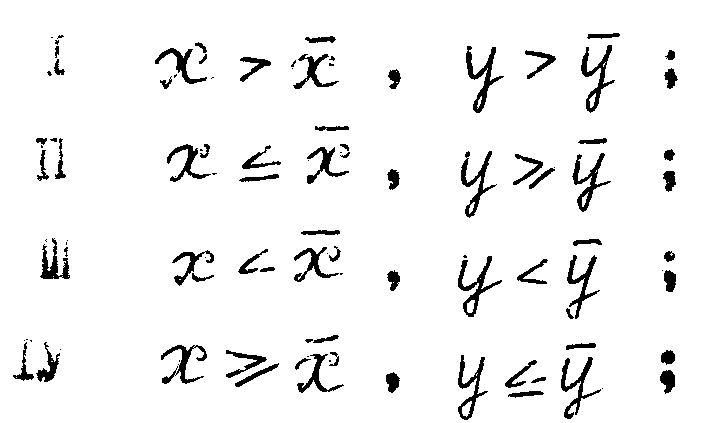
Области I и III взаимосвязаны, для них наблюдается положите­льная зависимость, а области II и IV обратно противоположные – отрицательная зависимость.



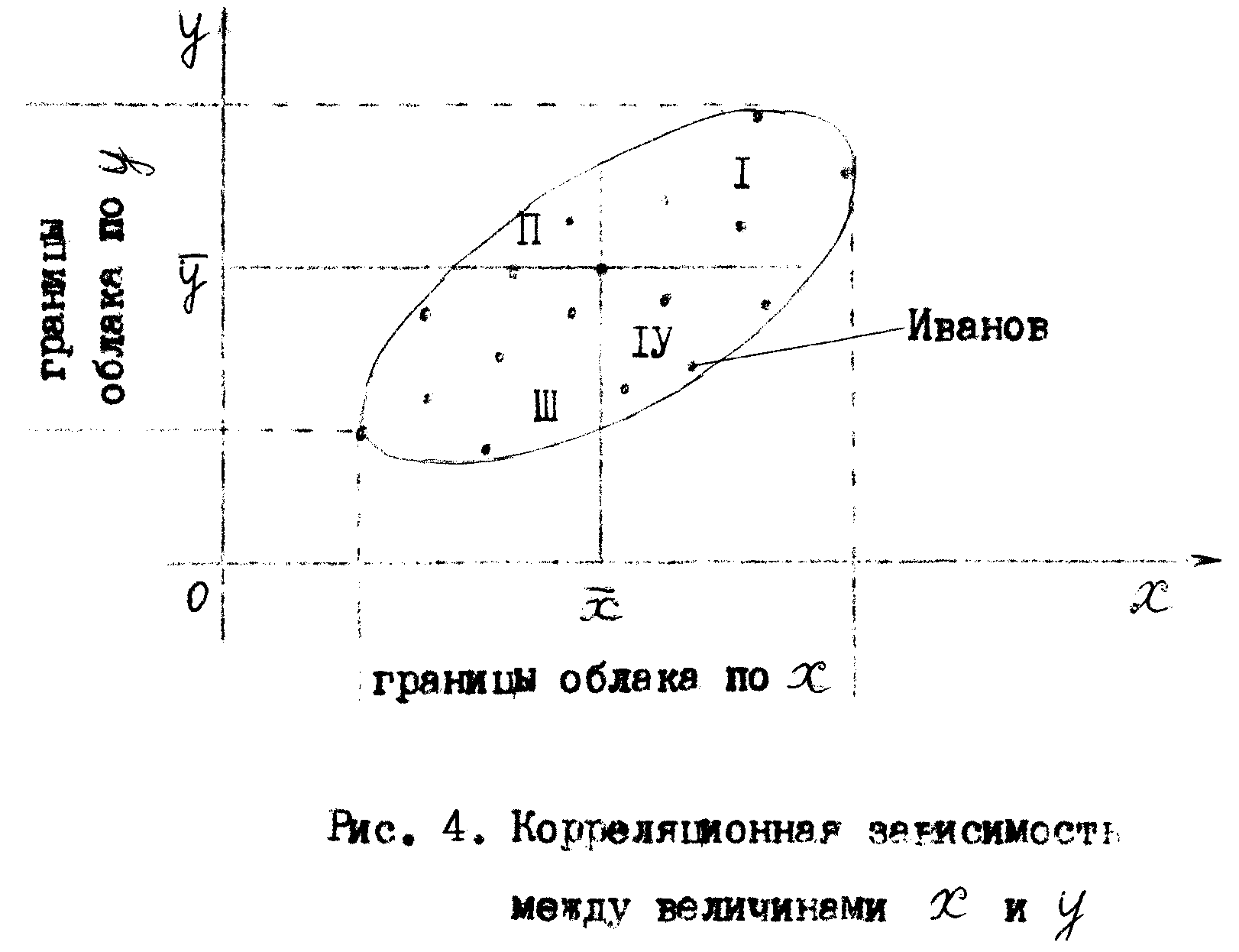
Подсчитаем число студентов по областям. Чем дальше точка (графический образ определенного студента) от среднего значения, тем больше вес (тем весомей голос) и, следовательно, более успешно осуществляется профессионально-методическая под­готовка данного студента. Каждому испытуемому, и в частности Иванову, можно сообщить его диапазон и сделать относительно его «среднее» предсказание. В нашем случае у Иванова высокий уровень подготовки по предметам методического блока, но он не умеет или затрудняется осуществлять перенос знаний в свою педа­гогическую деятельность в школе. На данном этапе обучения ему требуется помощь со стороны методиста и учителя.

Выберем теперь числовой индикатор, который бы различал ра­зные области на диаграмме рассеивания. Запишем это математи­чески:

(x1–x ) (y1–y) – для i-го студента. Это уже взвешенное «выражение».

Просуммируем данные "выражения" для группы студентов:



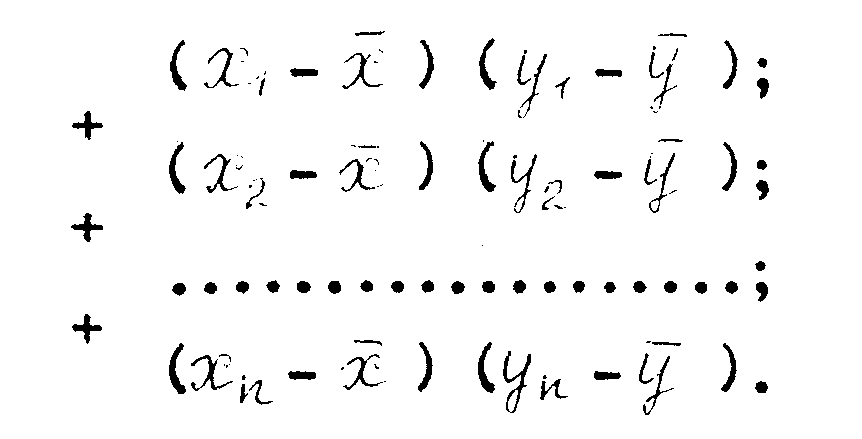
П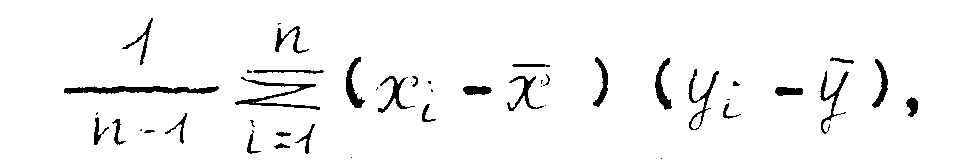ерепишем эту сумму в таком виде:

где n – число слагаемых (студентов). Это и будет «средний го­лос», так называемая ко вариация:




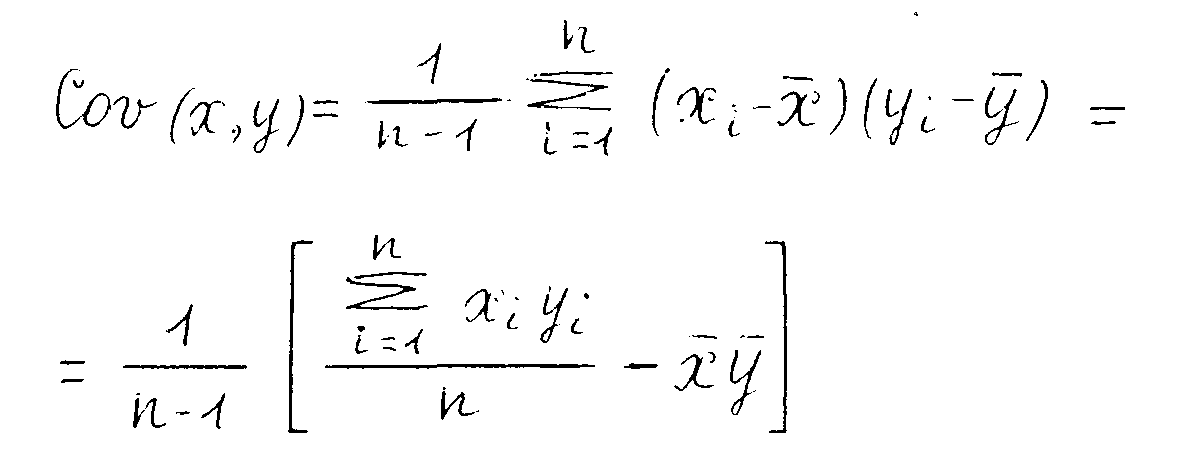
Представим себе, что мы выбросили из системы заданий, проверяющей уровень подготовки по предметам методического цикла, каждое 3-е задание. Это означает, что в среднем балл студента уменьшится, и, соответственно, явление, которое мы наблюдали выше относительно некоторого студента, осталось тем жe, но ковариация («средний голос») изменится, что не очень хорошо.

В данном случае для количественной оценки пользуются выборочным коэффициентом парной корреляции r_xy – безразмерной величиной, нормированной к значениям средних квадратических отклонений исследуемых величин S_x и S_y:



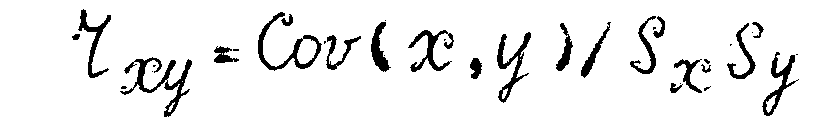
или общая формула:


К
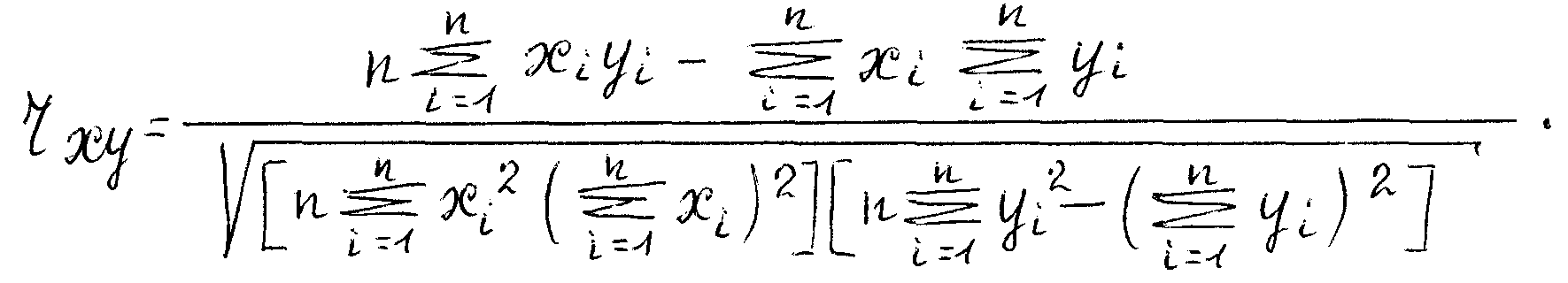
оэффициент корреляции может принимать следующие значения:

1) r_xy=0; случай соответствует отсутствию связи между x и у (рис. 5, а);

2) r_xy=+1; между x и у существует строгая положительная линейная связь (рис. 5, б);

3) r_xy=-1; между х и у существует строгая отрицательная связь (рис. 5, в);

4) -1 < r_xy < +1; это наиболее часто встречающийся случай, и здесь о корреляции судят уже лишь с точки зрения боль­шей или меньшей вероятности.

Коэффициенты парной корреляции могут быть рассчитаны не то­лько по формуле, написанной выше, но и непосредственно по уровням, по конечным разностям уровней и по отклонению от основной тенденции. Для этой цели воспользуемся уже полученными уравнени­ями.

Выравнивание уровня сформированности умения обучать уча­щихся самостоятельной работе с учебной литературой по физике проводилось по прямой y_t = 13,83 + 0,64t , уровня сформированности профессионально-методических умений в педагогической деятельности – по параболе второго порядка



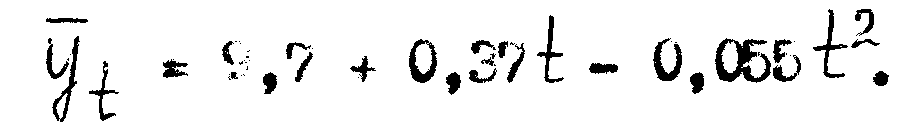
Здесь при вычислении корреляции учитывается вид тренда. Так, для уровня cформированности умения обучать учащихся само­стоятельной работе с учебной литературой учитываются первые разности (∆⁽¹⁾), а для уровня сформированности профессионально-методических умений в педагогической деятельности – вторые ра­зности (∆⁽²⁾). Для удобства вычисления обозначим в первом ура­внении x_t=y_t и тогда его можно записать:



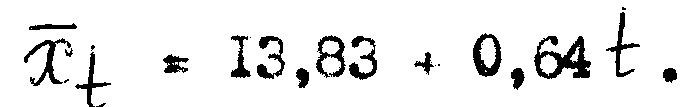
Коэффициент корреляциии для этого случая вычисляется по формуле:



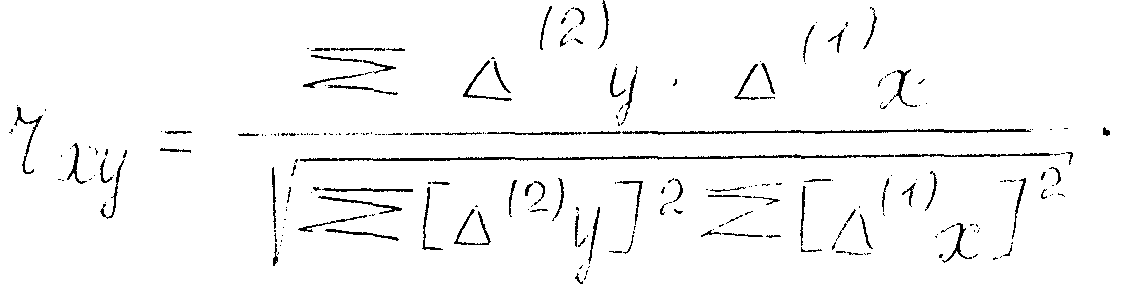
Допустим, мы подсчитали линейную корреляцию r_xy, испо­льзуя ту или иную формулу, сообщили диапазон и сделали «сред­нее» предсказание, но этого всегда мало для прогнозирования профессионально-методической подготовки данного студента. На успешность профессиональной подготовки оказывает влияние большое число переменных, это: успешность обучения по специальным предметам, предметам психолого-педагогического цикла; личност­ные свойства и качества студента; здоровье студента и т.д.

Исследование взаимных вероятностных связей большего чис­ла переменных намного сложнее исследования парной корреляции.

Покажем это на примере трех случайных величин x, y, z, которые следуют нормальному распределению и между которыми во­зможна линейная связь. Сначала вычисляются парные выборочные коэффициенты корреляции r_xz и r_yz аналогично парному коэффициенту r_xy, как было показано выше.

Однако, как показывает эксперимент, в нашем случае ме­жду x и y может наблюдаться связь, если имеет место одновременное воздействие на эти величины третьей переменной z. Тогда значение полного коэффициента, например r_xy, характеризует уже не корреляционную связь между х и у, а включает также часть корреляции, определяемой действием пе­ременной.

Обозначая коэффициент корреляции между х и у за выче­том корреляции с третьей величиной z через r_xy-z, выразим его через соответствующие парные коэффициенты корреляции r_xy, r_xz, r_yz :



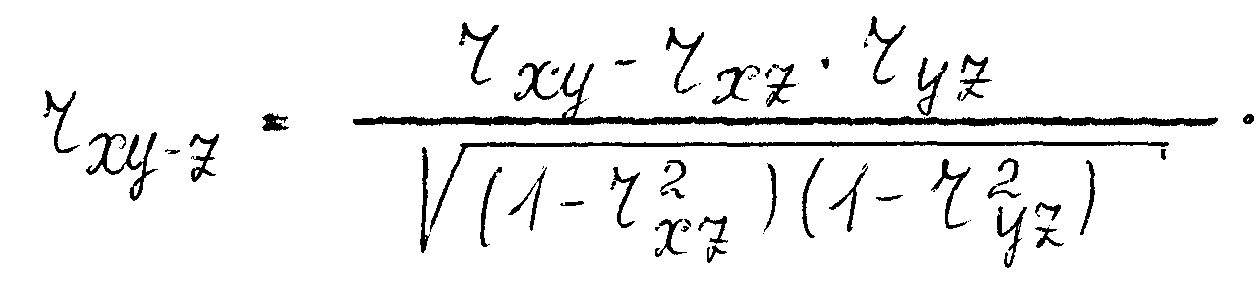
Так, если, например,






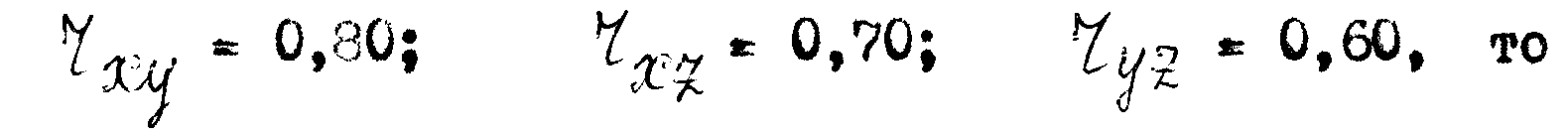
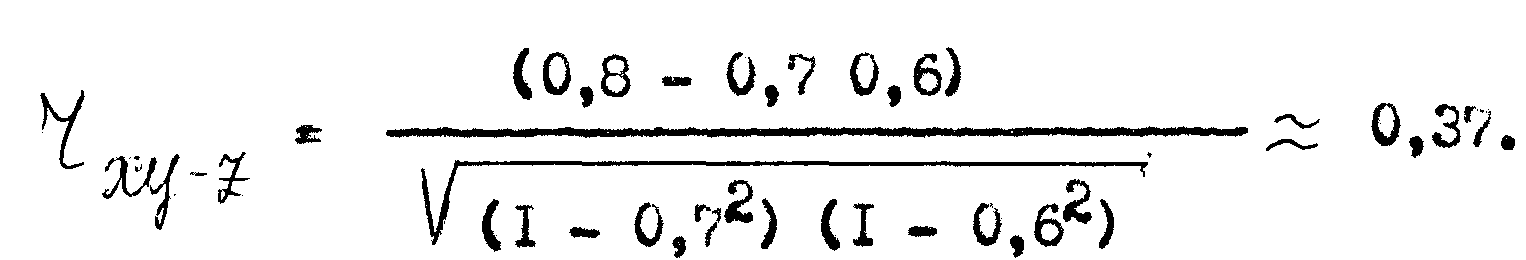
Таким образом, на долю корреляции между z и переменны­ми x и y приходится 0,80 - 0,37 = 0,43 от общего значения коэффициента корреляции, вычисленного без учета третьего факто­ра.

Аналогично можно вычислить коэффициенты r_xz-y и r_yz-x . Эти формулы получаются простой заменой букв при индексации.

Увеличение числа исследуемых переменных при корреляционном анализе позволяет решать новые задачи исследования связей. Решение таких задач с помощью стандартных программ ЭВМ не пред­ставляет труда.

Третье направление процесса прогнозирования профессиональ­но-методической подготовки связано с построением модели, кото­рая позволит сделать определенный прогноз для каждого студента.

Для примера возьмем динамические ряды, в которых х₁, х₂, х₃, …, х_n (х – успешность обучения i-го студента), а у₁, у₂, у₃, …, у_n (у – успешность педагогической деятельности i-го студента).

Тогда можно записать, что y=f(x) + ε. В записи заклю­чен глубокий смысл, здесь нет равенства в традиционном для мате­матикеи понятии. Это есть запись модели. Что больше влияет на успешность педагогической деятельности студента f(x) или некоторая случайная величина ε ?

Нам надо построить модель или записать уравне­ния регрессии.

Чертим диаграмму рассеивания. Пусть у нас будет некоторое облако (см. рис. 5).



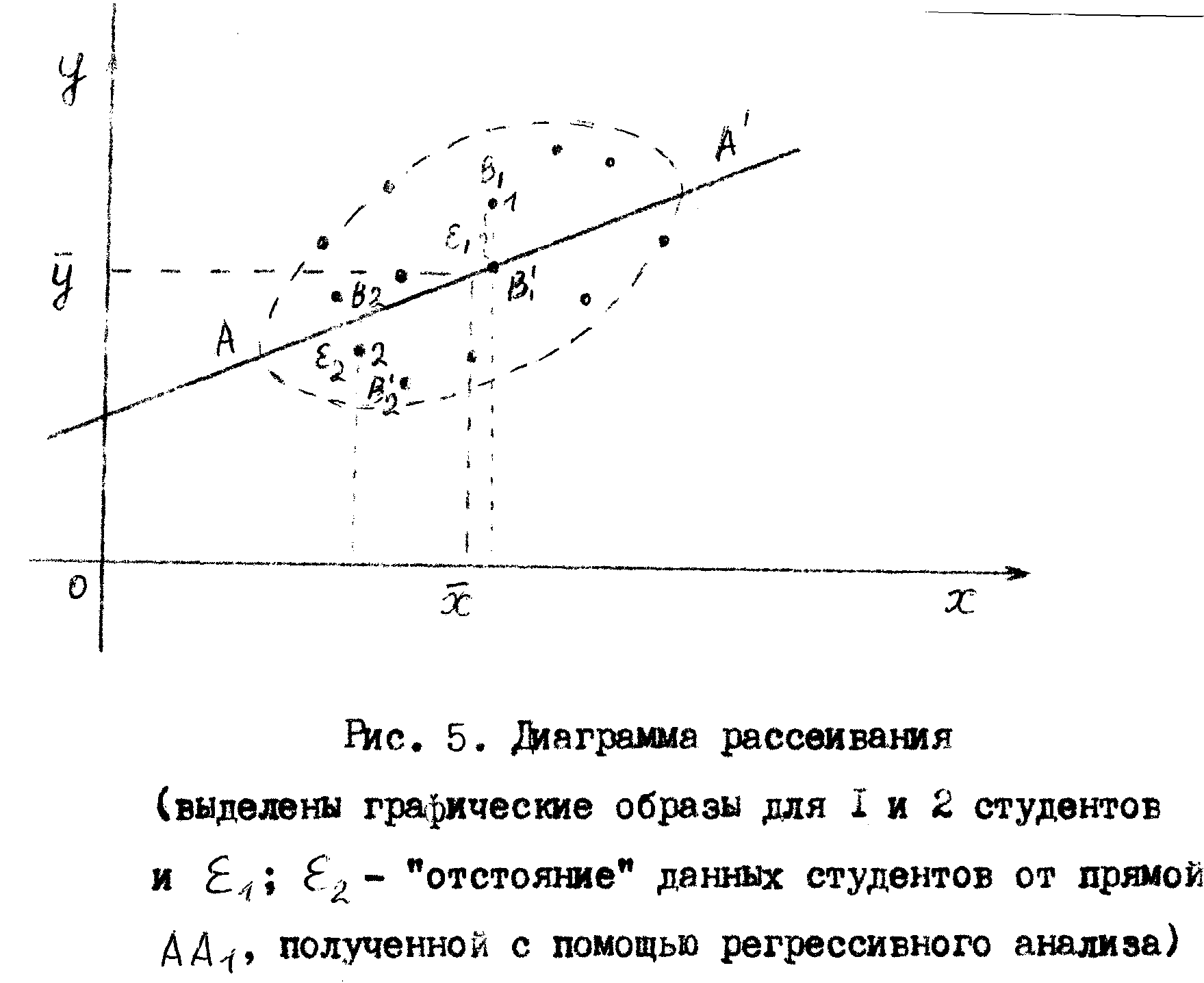
Приблизим наши данные к простой функции, а именно к линей­ным функциям. Мы как бы вводим понятие близости прямой к экспериментальным точкам и при этом должны так выбрать прямую, что­бы ошибки были минимальные и, соответственно, сумма



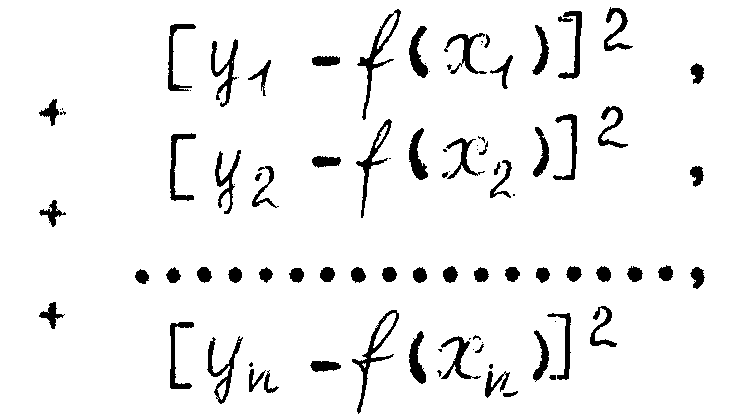
должна быть тоже минимальной.

Запишем нашу функцию в другом виде: y=b+a(x–x) – это тоже модель. Тогда сумма будет






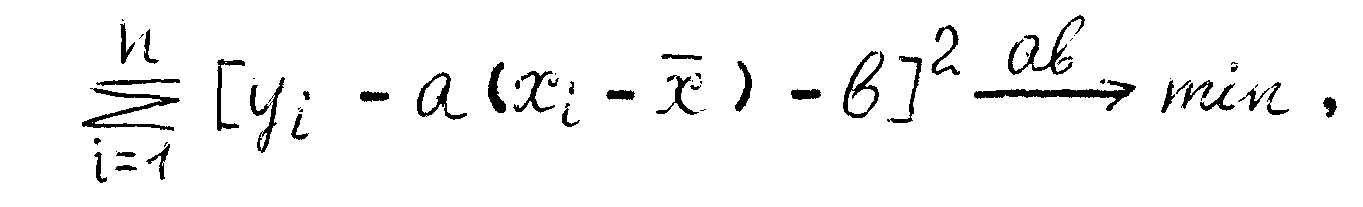
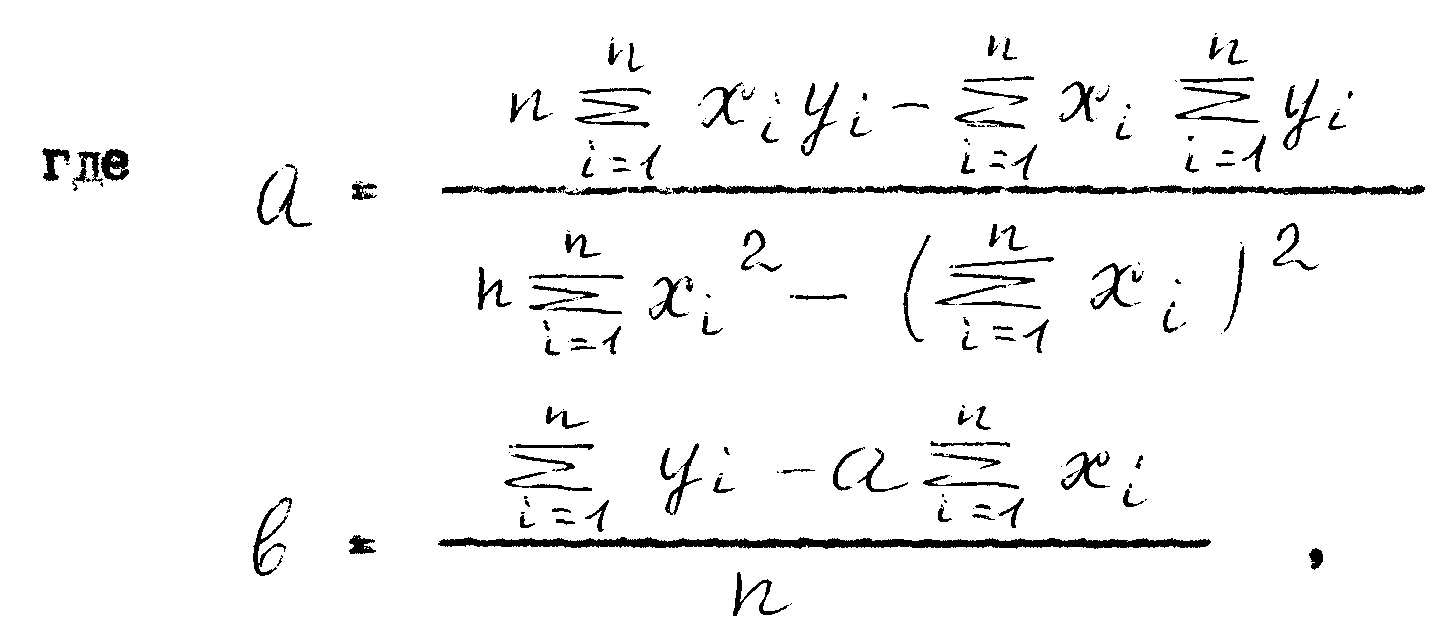
a и b – коэффициенты регрессии.

Статический анализ коэффициентов регрессии дает возмож­ность найти пределы измерения углового коэффициента и отрезка на оси ординат для линии регрессии, а исследование адекватно­сти позволяет оценить степень отклонения экспериментальных то­чек от этой прямой линии и тем самым оценить влияние случайной величины ε (см. рис. 5). В рассуждениях мы говорим о прямой линии, но, как видим, эмпирический способ сводится к постро­ению ломаной регрессии двух взаимосвязанных факторов по значи­тельному числу измерений. При этом можно воспользоваться изве­стным положением из математики: любую непрерывную функцию в достаточно узких пределах изменения аргументов можно прибли­женно заменить линейной. Ошибка при этом будет тем меньше, чем уже границы изменения аргументов и чем ближе функции к линей­ной.

Как мы видим, применение методов регрессивного анализа по­зволяет из нескольких различных по виду моделей выбрать наибо­лее адекватную, которую можно использовать для прогнозирования профессионально-методической подготовки студентов. Но наша за­дача усложняется тем, что приходится учитывать несколько неза­висимых переменных (факторов), и тогда анализ производят методами множественных регрессий.

Результаты анализа процесса профессионально-методической подготовки будущего учителя в педагогическом вузе показывают, что ее эффективность зависит от целого ряда факторов, которые нужно рассматривать не изолированно, а в их взаимосвязи. Вме­сте с тем, как показывает практика, учесть все взаимосвязанные факторы не представляется возможным. Поэтому следует произве­сти отбор наиболее характерных факторов, влияющих на результа­тивность профессиональной подготовки студента.

Исходя из анализа педагогической деятельности, для прогно­зирования профессиональной подготовки будущего учителя требу­ется многомерная модель. Для ее построения отобрано 19 показа­телей (факторов). Они могут быть для дальнейшего анализа на ЭВМ сгруппированы следующим образом:

1. Результативные показатели эффективности профессиональ­но-методической подготовки: х₁ – средний уровень сформированности профессионально-методических умений;

х₂ – средний коэффициент сформированности профессионально-методического умения







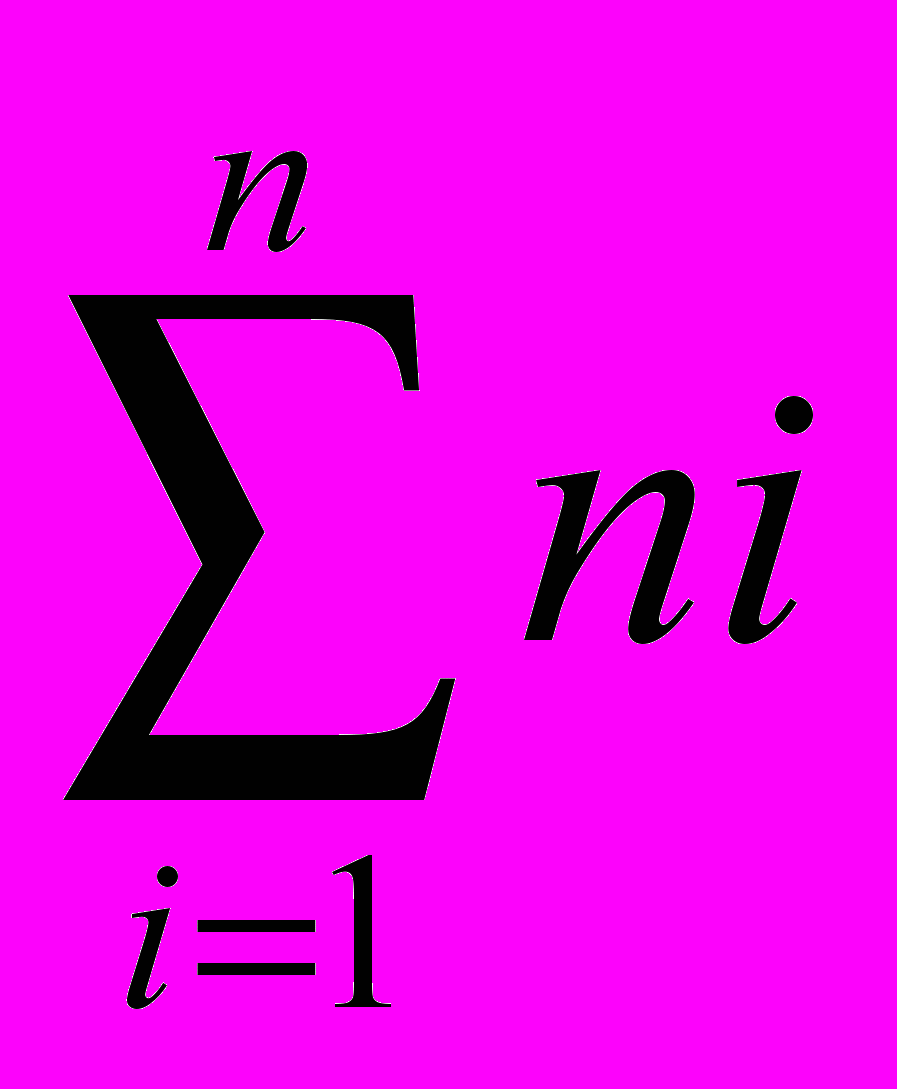
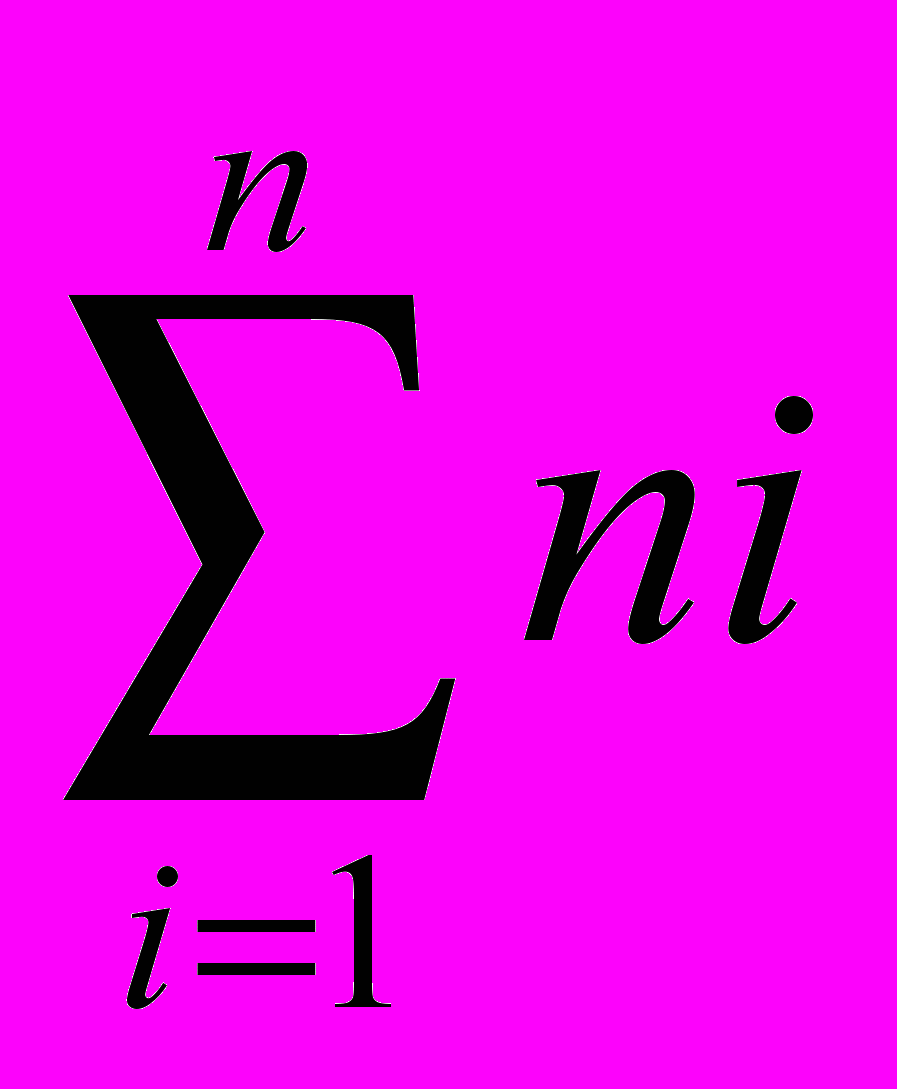
(k == –––––––––, где – количество верно выпол-

n


ненных операций i-м студентом, n – максимальное число операций, которое должно быть выполнено); х₃ – успешность обучения по специальным предметам; х₄ – успешность обучения по предметам психолого-педагогического блока; х₅ – успешность обучения по предметам методического блока; х₆ – достижение в обучении (по предметам методического цикла); х₇ – достижение в обучении (по специальным предметам); х₈ – достижение в обучении (по предметам психолого-педагогического цикла); х₉ – уровень успешности педагогической деятельности на практике.

2. Факторные показатели (факторы): х₁₀ – особенности ка­чества и свойства личности; х₁₁ – средняя продолжительность учебного дня; х₁₂ – условия для индивидуальной и самостоятель­ной работы; х₁₃ – организация научно-исследовательской работы студентов; х₁₄ – организация профессионального обучения (соде­ржание, формы, методы и средства); х₁₅ – обратная связь; х₁₆ –бытовые условия; х₁₇ – материальное положение студента; х₁₈ – здоровье студента; х₁₉ – управление процессом обучения.

Все эти показатели, как показывает эксперимент, в целом характеризуют эффективность профессионально-методической подго­товки будущего учителя. Из них с помощью всестороннего анализа и тщательного изучения парных коэффициентов корреляции можно отобрать наиболее существенные, влияющие на уровень профессиона­льно-методической подготовки студента.

Так как уровень профессионально-методической подготовки за­висит от нескольких независимых переменных (показателей) х₁, х₂, …, х_n, то его прогнозирование для каждого студента производят методами множественной регрессии. Наибольший практи­ческий интерес представляет множественная линейная регрессия, уравнение которой имеет вид:



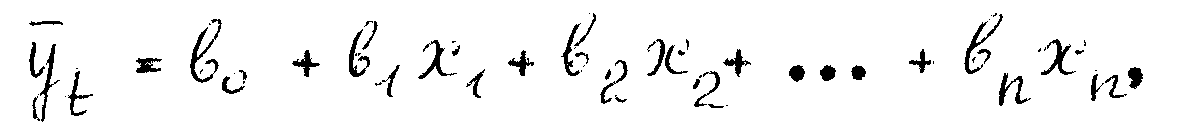
где b – прогнозные значения параметров.

Как уже отмечалось, при сравнительно небольших диапазонах изменения факторов любую кривую всегда можно представить в ви­де прямой с определенной степенью точности. Подставляя в нее значения параметров успешности обучения и факторных признаков, получаем прогнозные значения моделируемого показателя профес­сиональной подготовки каждого студента.

Многофакторное прогнозирование на основе данной методики возможно при следующих условиях:

1. Формирование профессионально-методического знания, уме­ния у студента происходит в соответствии с принципом инерции, т.е. есть все основания предполагать, что закономерности, под­меченные в изучаемом периоде, будут сохраняться и в будущем.

2. Период измерения показателей достижения испытуемых до­лжен быть выбран правильно.

3. Создание эффективных способов измерений, позволяющих объективно и с необходимой точностью оценить результаты обуче­ния.

Одним из важнейших методологических моментов многофактор­ного прогнозирования, на наш взгляд, является вопрос об адеква­тности построенных моделей. Мы понимаем, что любые модели – это некоторая идеализация действительности. Положенные в их основу предпосылки (требование однородности статистического материала, достаточное число наблюдений, отбор обоснованных факторных признаков с точки зрения их количества, независимости, способа расчета) никогда не соблюдаются полностью. Вопрос заключается даже не в том, соблюдать эти предпосылки полностью или нет, а в том, насколько велико отклонение модели от реальности. Нару­шение отдельных предпосылок построения многофакторных моделей не снижает их ценности и не делает их непригодными. Важно, что­бы логическое содержание модели соответствовало задачам иссле­дования.

Метод многофакторного прогнозирования дает хороший результат в сочетании с ЭВМ, так как большинство необходимых вычислений запрограммировано, и все это позволяет за короткое время, при на­личии эффективных способов измерений, отследить изменения уровня профессионально-методической подготовки каждого студента. Сказанное выше требует создания в вузе хорошо управляемых техно­логий обучения, а это, в свою очередь, предполагает создание сис­темы педагогических тестов, позволяющих объективно оценить раз­личные стороны процесса обучения студентов и его результаты.


Литература

1. Причины отсева студентов из педагогического вуза (по мне­нию студентов и преподавателей). – Красноярск: Изд-во КГПУ, 1995. – 54 с.
   
2. Загвязинский В.И. Педагогическое предвидение // Новое в жизни, науке, технике. Сер. Педагогики и психология. — 1987. – № 4. – С. 79.
   
3. Гендин А.М. Предвидение и цель в развитии общества. Крас­ноярск, 1970. – 436 с.
   
4. Дейвисон М. Многомерное шкалирование: Методы наглядного представления данных). – М.: Финансы и статистика, 1988.
   
5. Михеев В.И. Моделирование и методы теории измерений в пе­дагогике: Научно-методическое пособие. – М.: Высшая школа, 1987. –200 с.
   

ОБ ИНТЕГРИРОВАННОЙ СИСТЕМЕ КОМПЬЮТЕРНОГО
ТЕСТИРОВАНИЯ

Пак Н.И., Филиппов В.В.




Филиппов Виктор Викторович, 1966 г. рождения, аспирант, общее количество публикаций – 10, в том числе: Пак Н.И., Филиппов В.В. О технологии создания компьютерных тестов. // ИНФО. –№ 5. – 1997.


Система образования в открытом обществе нуждается в четком и постоянном механизме государственного контроля качества образования. Контроль на основе образовательных стандартов чаще осуществляется субъектами образовательного процесса и носит традиционно весьма субъективный характер.

Повысить объективность государственного контроля за качеством образования может общенациональная система компьютерного тестирования, основным компонентом которой является открытый банк тестовых заданий предметной области. Второй важной компонентой системы должна стать метрологическая трехмерная (рейтинг, зачет, оценка) шкала измерения уровня обученности.

Для создания компьютерных тестов созданы и разрабатываются универсальные и специализированные тестовые оболочки. Однако их наполнение вызывает трудности у педагогов-практиков в силу отсутствия простых и эффективных методик создания тестовых заданий.

Одним из путей решения проблем построения систем тестирования является кибернетический подход, основанный на принципах «белого» и «черного» ящика, формализации и структурировании знаний предметной области в виде семантического графа [1].

Порядок создания теста и проведения тестового эксперимента можно представить как последовательность следующих этапов:



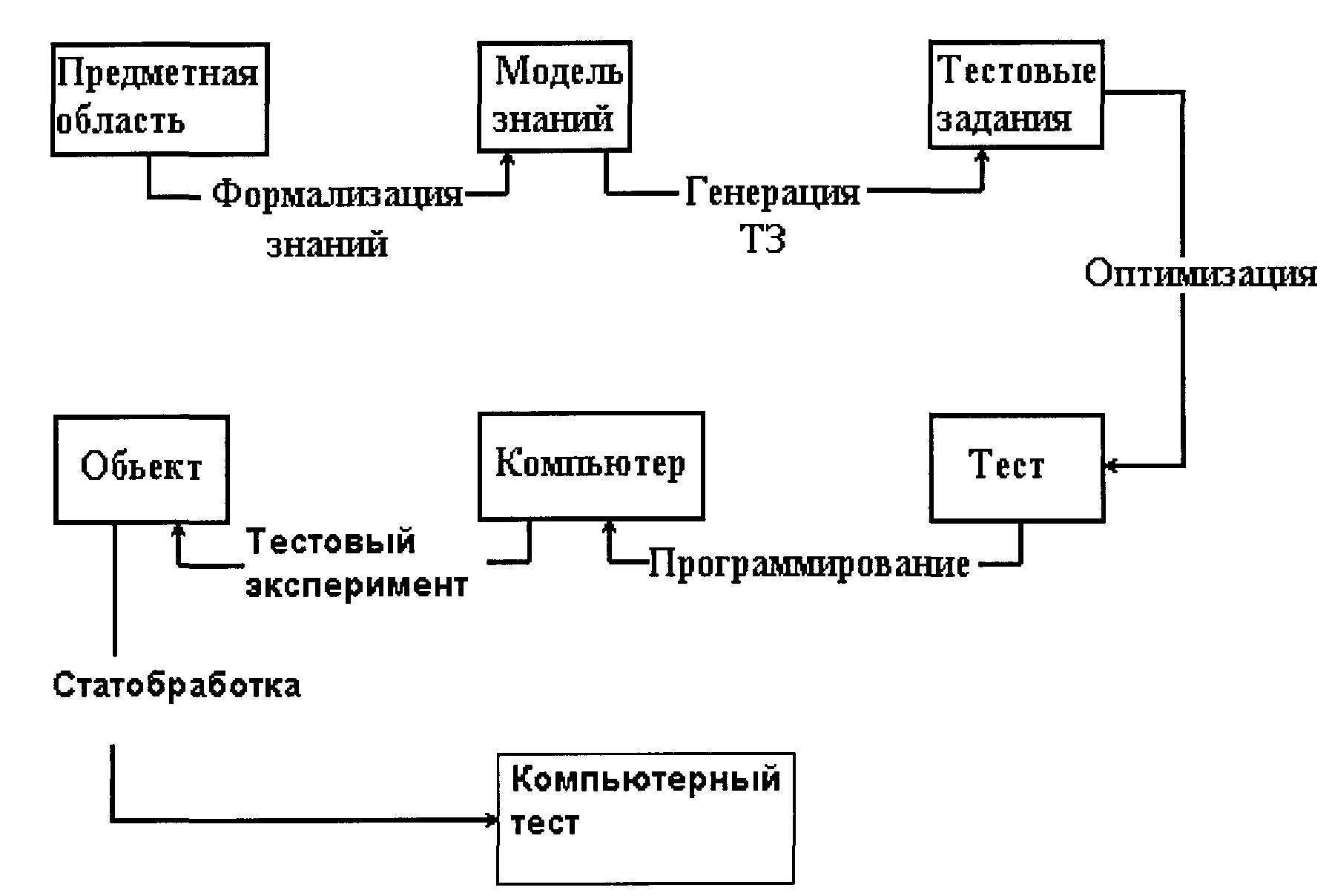
Создание теста необходимо начинать с определения предметной области. Затем необходимо сформировать модель знаний путем формализации по какому-либо способу, например, построением графа понятий и характеристик предметной области [1], либо описав содержание курса и требования к знаниям и умениям обучаемого. Уровень формализации часто зависит от целей и задач предполагаемого контроля (итоговый, текущий, рубежный). Эти факторы определяют необходимый набор тестовых заданий, которые можно создавать, генерировать, используя различные методы. Оптимизацию создаваемого теста можно проводить экспортно либо экспериментально, в частности, можно использовать технологию моделирования. Далее можно приступать к созданию компьютерного варианта теста, используя инструментальные оболочки или системы программирования. Заключительным этапом тестового эксперимента является анализ его результатов и статистическая обработка с целью корректировки уровней сложности, шкал измерения (оценка качества) знаний, создания эффективного теста.

Рассмотрим подробнее все этапы на частном примере. Попытаемся создать фрагмент теста одного предметного модуля из школьной математики 5-6 классов – действия над натуральными числами.

В качестве модели знаний будем использовать структуру, описанную в [1]. Введем понятия: Натуральное число, Сложение, Умножение, Вычитание, Деление, Арифметическое выражение.



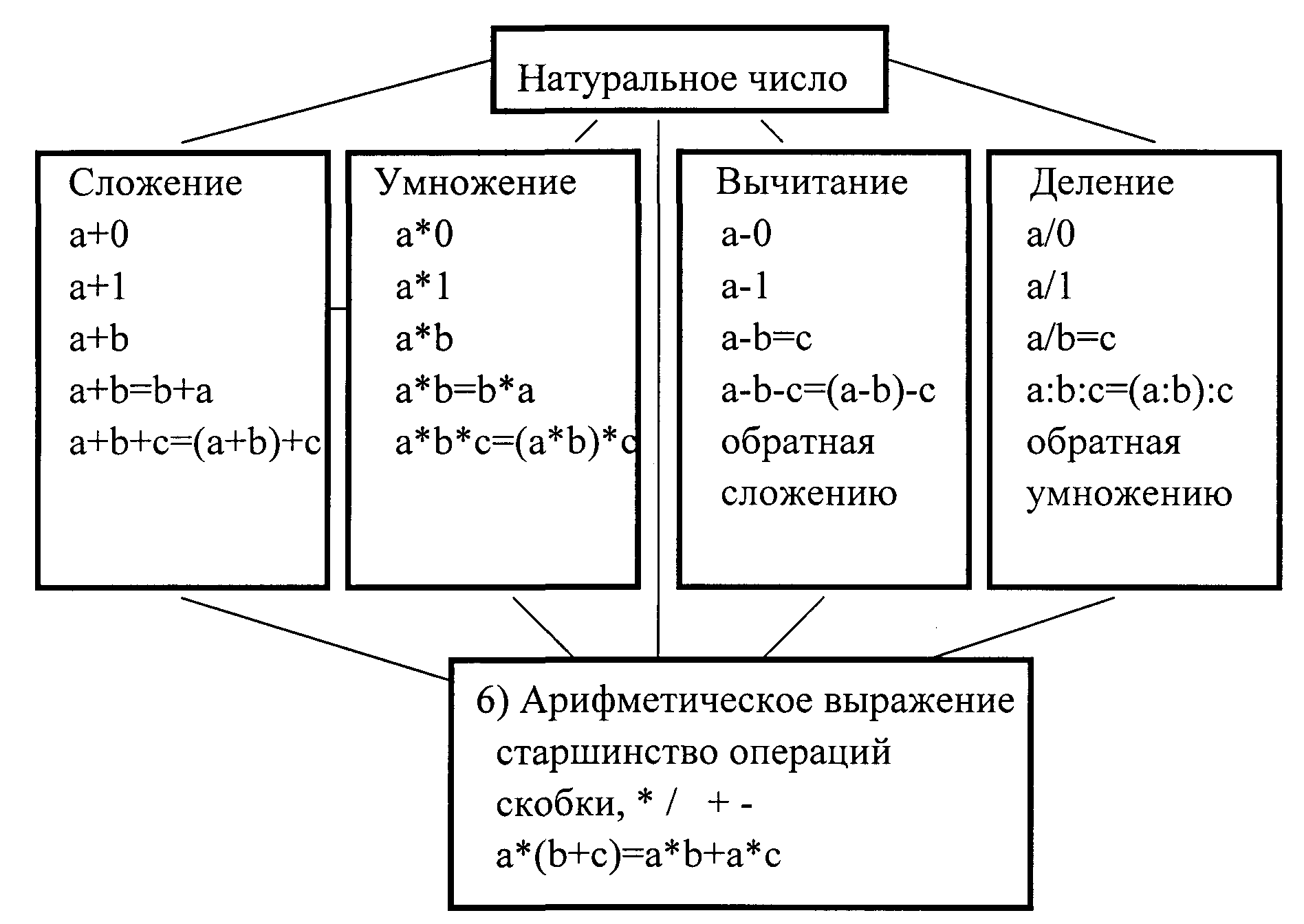
Для каждого понятия, входящего в модуль, описаны его свойства.

На следующем этапе возникает проблема заполнения базы данных тестовых заданий. Согласно [2], используем три принципа построения ТЗ:

1. Полный опрос свойств – тестирование фактологических знаний.

2. Покрытие путей – тестирование аналитических знаний.

3. Покрытие алгоритмов и задач – тестирование алгоритмических умений.

Рассмотрим примеры тестовых заданий:

1. а) Какие из перечисленных чисел являются натуральными:

1,3 3/5 2 0.

б) Арифметическое выражение содержит: операцию сложения, операцию умножения, операцию сложения и умножения, все операции.

2. а) Результатом сложения двух натуральных чисел является:

натуральное число, ненатуральное число, дробное число.

б) Результатом деления двух натуральных чисел является:

натуральное число, ненатуральное число, дробное число.

3. а) Истинным является:

а + (b+c)-a+b + а+с, a(b+c)-ab+ac, a+(ab)-(a+a)(a+b).

б) Вычислите выражения, используя распределительный и сочетательный законы:

13*48+13*52=

97*127-97*27=

157+678+143=

156*364*11=


Следующая проблема – определение уровня сложности и качества тестового задания.

Для оценки сложности примем за основу классификацию ЛАТ [3]. В отличие от системы ЛАТ, классификацию будем проводить для каждого способа построения тестовых заданий:

Полный опрос : М – мировоззренческий

Б – базовый

П – программный

С – сверхпрограммный

Покрытие путей: Ф– фактологический

О – операционный

А – аналитический

Т – творческий

Покрытие задач: Мо – механический, одношаговый

Ac – алгоритмический, стандартный по образцу

На – нестандартный, алгоритмический

И – исследовательский, новый метод

Показатели сложности ТЗ:

1) уровень фактологический;

2) уровень аналитический;

3) уровень алгоритмический.

Показатели качества ТЗ:

1. Информативность.

2. Понятность, ясность.

3. Валидность – пригодность.

4. Надежность.

5. Вероятность угадывания.

6. Интерфейс.

7. Мотивация.

8. Универсальностью

9. Психологичность.

10. Корректность ТЗ.

11. Удобство применения.

Эти показатели полезно оценивать на всех этапах создания ТЗ, что позволит планировать уровень сложности, контролировать показатели сложности и качества в процессе разработки, выбирать базовые образцы по классам эквивалентности.

Качество (и сложность) ТЗ выражается баллом (баллами (?)) задания.

ТЗ из одного класса эквивалентности имеют одинаковые свойства по баллу, времени выполнения, сложности и т.п.

Всем тестовым заданиям присваивается балл качества (сложности, надежности) от 1 N. Этот балл определяется как среднее значение суммы экспертных баллов с учетом весовых коэффициентов. Веса свойств ТЗ определяются либо экспертно, либо по результатам тестирования.

Предварительно каждому ТЗ выставляется балл или нормировочный коэффициент. Уточнение и корректировка оценок производится по завершении тестирования или по какой-либо схеме (см. ниже).

Разбалловка позволяет оценивать по рейтингу, порогово, оценочно (экспертно по долям: по распределению экспериментальных данных, например, свыше 90 % – отлично, менее 50 % – три, менее 35% – неуд.).

Среди методов оценивания показателей сложности ТЗ выделим экспертный, статистический, аналитический, социологический.

Экспертный метод осуществляется группой экспертов-специалистов, компетентных в предметной области, на базе их опыта и интуиции. Применяется, когда задача не может быть решена никаким другим способом или другие способы являются более трудоемкими и менее точными. Рекомендуется применять при определении показателей информативности, понятности, оценки интерфейса и т.п.

Статистический метод предполагает измерение или учет выделенных показателей качества и формирование оценок методами статистики.

Аналитические методы базируются на математических моделях, связанных с моделью знаний, семантическим графом и т.п.

Социологический метод основан на обработке специальных анкет-вопросников.

Для всех этих методов полезно формировать базу данных тестовых заданий со следующей структурой:

1. Шифр (номер ТЗ, тема, раздел).

2. Класс эквивалентности.

3. Форма ТЗ (открытая, каноническая).

4. Задание.

5. Ответ 1.

6. Ответ 2.

7. Ответ 3.

8. Ответ 4.

9. Ответ 5.

10. Ключ правильного(ых) ответа(ов).

11. Тип ТЗ (полный опрос, покрытие путей, покрытие задач (фактологический, аналитический, алгоритмический)).

12. Сложность по знаниям фактологическим.

13. Сложность по знаниям аналитическим.

14. Сложность по умениям (алгоритмические знания).

15. Информативность (вес 1).

16. Понятность, ясность (вес 2).

17. Валидность – пригодность (вес 3).

18. Надежность (вес 4).

19. Вероятность угадывания (вес 5).

20. Интерфейс (вес 6).

21. Мотивация (вес 7).

22. Универсальность (вес 8).

23. Психологичность (вес 9).

24. Корректность (вес 10).

25. Удобство применения (вес 11).

26. Балл (по сложности + весовые коэффициенты).

27. Время выполнения.

28. Возраст.

Критерии (веса) по качествам ТЗ позволят проводить фильтрацию ТЗ. Какие-то свойства должны влиять на сложность (балл), а какие-то – являться фильтрами для включения в банк ТЗ.

Сформулируем экспертные требования к составлению тестовых заданий:

– ТЗ должно быть исключительно прямым по своему содержанию.

– Ответы на ТЗ не должны быть контрастными ни по форме, ни по содержанию, ни по смыслу.

– Комфортность для тестируемого достигается короткими вопросами и короткими тестами.

– В тесте должна быть идеология, мотивация для тестирования: конкурентного (порогового, рейтингового, оценочного), сравнительного, количественного, психологического, качественного.

Критерии составления теста

При наличии базы данных тестовых заданий имеется возможность генерировать целевые тесты. Выделяют простые и составные тесты. Составной тест целесообразно составлять при большом количестве разделов и тем, при автономных и независимых модулях знаний большого объема как совокупность простых тестов. Простой тест формируется по следующим критериям:

временной критерий;

критерий по баллам;

критерий пропорциональности;

количественный критерий;

вид контроля;

режим тестирования;

шкала измерения знаний.

Рассмотрим эти критерии подробнее.

1. Временной критерий имеет три ограничения по времени: жесткое, мягкое, безлимитное. При жестком ограничении формирование теста совершается из совокупности ТЗ по заданному общему времени его выполнения. Мягкое ограничение допускает формирование ТЗ по задаваемому интервалу времени.

2. Критерий по баллам также может быть жестким, мягким и безлимитным:

• Жесткий: формирование теста по одинаковой суммарной сложности ТЗ.

• Мягкий: формирование теста по интервальной сложности ТЗ.

• Безлимитный: ограничение по баллам отсутствует.

3. Критерий пропорциональности допускает формирование теста из ТЗ разных тем, разделов пропорционально их объему, либо по определенному количеству ТЗ из разделов и тем, а также выборками случайным образом.

4. Количественный критерий очевиден: допускается формирование теста по заданному количеству ТЗ, по запросу пользователя и без ограничения.

5. Вид контроля определяет контроль промежуточный (тест по заданному разделу) и итоговый (по всем разделам).

6. Режим тестирования. Поскольку тесты могут быть использованы при контроле, тренаже и обучении, то при их формировании необходимо учитывать режим их использования.

7. Шкала измерения задает форму оценивания знаний:

– Рейтинговая (по общей сумме набранных баллов).

– Пороговая (задание критического значения балла, например для установления допуска, зачета, уровня и т.п.).

– Оценка (задание критерия соответствия балла оценке, к примеру –2,3,4,5).

Рассмотрим особенности методики составления компьютерного теста с помощью экспертного метода. Предполагается, что объективность измерения уровня обученности с помощью тестирования может быть достигнута при условии, что банк педагогических тестов наполняется и экспертируется большим числом специалистов-предметников из разных регионов страны. Выбор критериев и меры оценки результатов тестирования осуществляется путем анализа экспертных предложений, полученных на основе статистических данных тестирующего эксперимента.

Главным условием создания эффективного и объективного теста является его массовое экспертное формирование и актуализация. Структура и телекоммуникационные возможности сетей передачи данных Министерства образования и Министерства науки, а также учреждений среднего и педагогического образования могут позволить обеспечить массовый сбор тестовых заданий и их экспериментальную апробацию на большом числе испытуемых.

Разрабатывается экспертная модель знаний предметной области. Предлагается форма тестовых заданий и технология формирования тестовых заданий. Создается план-график проведения тестирующего эксперимента и сбора его результатов.

Организуется республиканская телеконференция по разработке и сбору тестовых заданий. На этой основе формируется банк тестовых заданий {тестовое пространство}, а затем происходит компьютерное наполнение (после фильтрации тестового пространства) интегрированной тестовой системы.

Тестовый эксперимент с участием большого числа экспертов и испытуемых в разных учреждениях образования и в разных регионах позволит сформировать объективный и качественный тест с хорошим уровнем измерения знаний и умений тестируемого.

Затем тест подвергается сертификации экспертной комиссией по образовательным стандартам.

Известно, что при тестировании на учащегося и, следовательно, на результат тестирования влияет большое количество различных факторов, например, фактор ограничения по времени. Очевидно, что игнорирование любого значимого фактора понижает надежность теста. Значимые факторы определяют по результатам тестового эксперимента. Для решения возникающей задачи могут использоваться методы экспертного ранжирования, корреляционного и факторного анализа. В частности, выбрав экспортно m значимых факторов, выделим из них m1 независимых факторов (m1 – базис в пространстве факторов M). Базис независимых факторов будет влиять на коэффициенты сложности и веса тестовых заданий. Для их поиска могут быть использованы методы статистики, главных компонент, повороты пространства М и т.д.



Для иллюстрации сказанного приведем частный пример.

Обозначим за X_ij балл ответа на i-е задание j-м учеником, а за Y_i – весовой коэффициент по выбранному фактору. Рассмотрим выражение Σ (X_ij * Y_i) - Z_j, где Z_j – экспертная оценка j ученика. Можно предложить функционал ошибки теста

Σ ( Σ (X_ij * Y_i) - Z_j)² и минимизировать его подбором весов Y_i, J _i

Реализовать предложенную технологию создания и использования компьютерных тестов может позволить интегрированная среда компьютерного тестирования.

Общая схема функционирования интегрированной среды




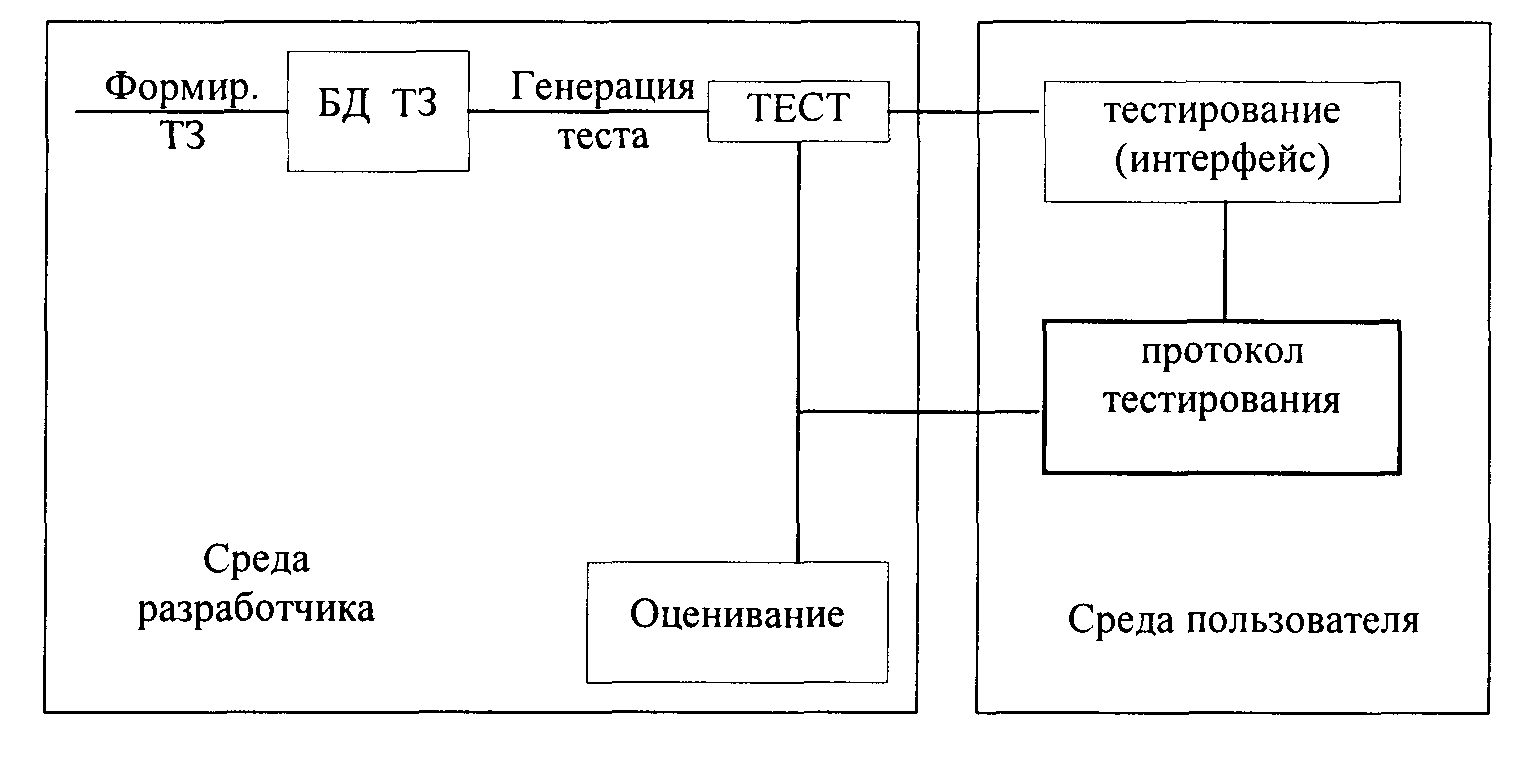
Сетевой вариант (клиент-сервер)



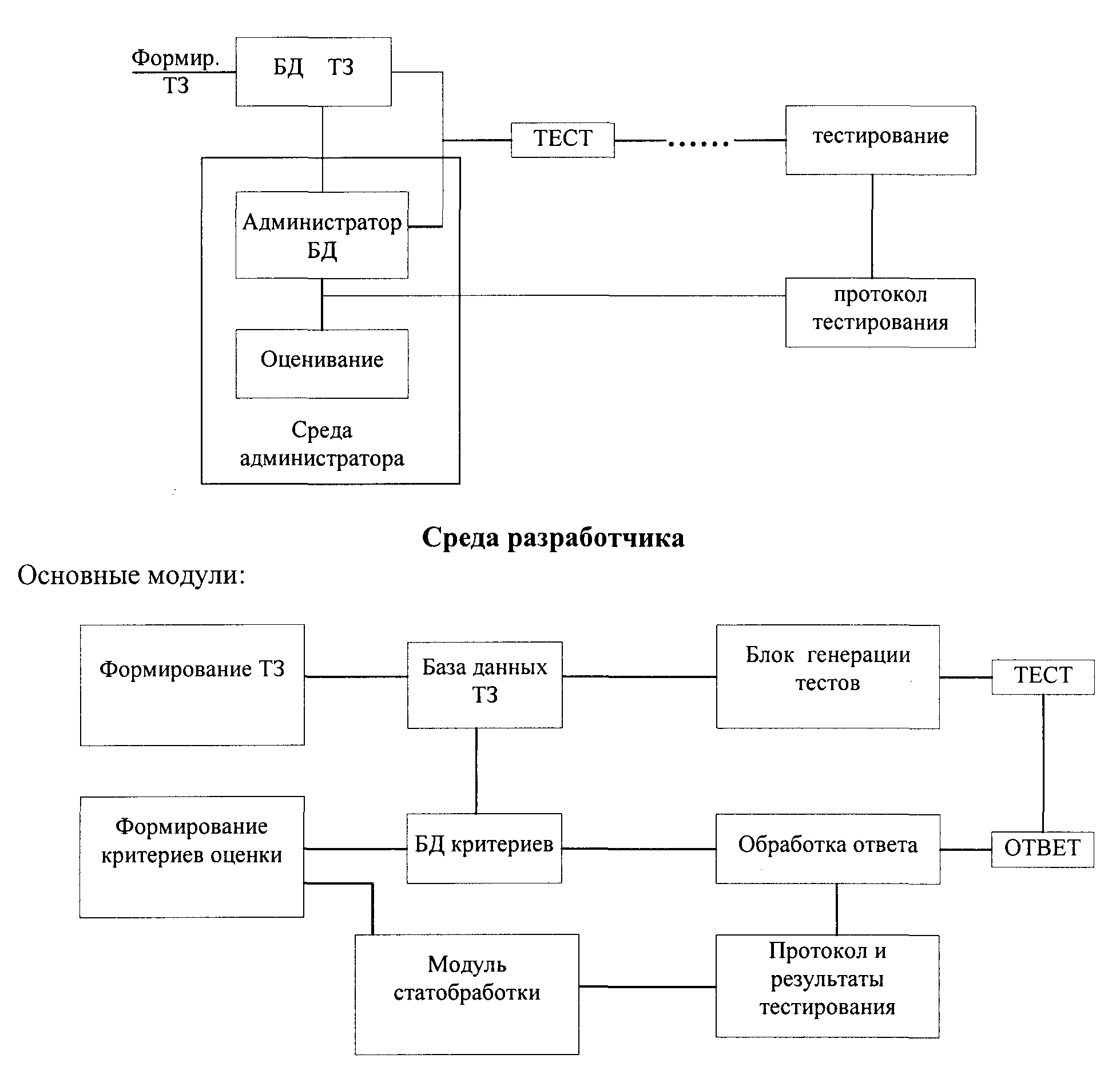
Систему компьютерного тестирования удобно формировать по клиент-серверной технологии. Интегрированную среду компьютерного тестирования можно условно разделить на три составляющие блока: разработчика, пользователя и администратора. Блок администратора размещают на WWW-сервере, SQL-сервере и сервере приложений. Среда разработчика и среда пользователя (клиентская часть) используют какой-либо интернетовский браузер и запросную систему к банку тестовых заданий и библиотекам интегрированной тестирующей среды. Среда администратора осуществляет идентификацию запроса пользователя и протоколирование тестирования.

Преимущества и возможности интегрированной системы компьютерного тестирования:

1. Создаваемая система вводится в эксплуатацию поэтапно, является распределенной (по предметным областям знаний, по серверам региональных узлов и т.п.), функционирует постоянно и непрерывно совершенствуется.

2. Система позволяет решить многие государственные задачи образования:

А) совершенствовать механизмы стандартизации контроля качества обучения, стандартизации измерения уровня обученности;

Б) совершенствовать и оптимизировать систему промежуточного и итогового контроля знаний по предметной области для школы и вуза.

В) совершенствовать и оптимизировать учебные планы, рабочие программы и методики обучения.

3. Система является ключевым звеном для дистанционного образования.

4. Система предоставляет образовательные услуги всем слоям населения (для тренажа, самоконтроля, для получения сертификата, обучения).

5. Система позволяет решать многие задачи органов управления образованием: Министерства образования, департаментов образования, учебных управлений вузов.


Литература

1. Пак Н.И., Филиппов В.В. О технологии компьютерного тестирования // ИНФО. – № 5. – 1997.
   
2. Пак Н.И., Симонова А.Л. Методика составления компьютерных тестов // ИНФО. – № 4, – 1998.
   
3. Родионов Б.У., Татур А.0. Стандарты и тесты в образовании.– М., 1995.– 48с.
   

ИЗ ОПЫТА ПОДГОТОВКИ УЧИТЕЛЯ ИНФОРМАТИКИ МЛАДШЕЙ ШКОЛЫ В КРАСНОЯРСКОМ ГОСУДАРСТВЕННОМ ПЕДАГОГИЧЕСКОМ УНИВЕРСИТЕТЕ