Готфрид вильгельм лейбниц сочинения в четырех томах том 3

Вид материала

Документы

Содержание Лейбниц — мальбраншу Лейбниц — мальбраншу С или (С), ординату СВ

Подобный материал:

• Готфрид вильгельм лейбниц сочинения в четырех томах том , 8259.23kb.
• Монадология, 209.43kb.
• Готфрид вильгельм лейбниц сочинения в четырех томах том, 9222.8kb.
• Лейбниц Г. В. Сочинения в четырех томах:, 241.84kb.
• Готфрид Вильгельм Лейбниц, 94.22kb.
• Лейбниц Готфрид Вильгельм (Leibniz Gottfried Wilhelm) немецкий ученый (философ, математик,, 271.47kb.
• Лейбниц (Leibniz) Готфрид Вильгельм (1646-1716), немецкий философ, математик, физик,, 201.35kb.
• Установочная лекция вткс, 212.41kb.
• Георг Фридрих Риман Готфрид Вильгельм Лейбниц литература, 208.32kb.
• Источник: Чехов А. П. Полное собрание сочинений и писем в тридцати томах. Сочинения, 565.43kb.

ЛЕЙБНИЦ — МАЛЬБРАНШУ

22 июня 1679 г.

Я получил Ваше письмо, за которое премного благодарен. Немного позже я получил и «Размышления о метафизике», автором которых тоже могу считать только Вас или по крайней мере этого г-на аббата Катлана, которому Вы приписываете «Христианские беседы», человеку, по всей видимости, талантливому и полностью усвоившему Ваш образ мыслей. Эти «Беседы» я читал не так, как читают обычную книгу, но с особым вниманием, и, если Вы согласны снизойти к моей простоте, я скажу Вам, что я о них думаю. Я горячо одобряю оба положения, выдвигаемые Вами, а именно что все вещи мы видим в Боге и что тела не воздействует на нас сами по себе. Я всегда был убежден в этом в силу великих доводов, кои представляются мне неопровержимыми и зависят от некоторых аксиом, нигде еще, насколько я знаю, не использованных, хотя их можно было употребить с огромной пользой для доказательства некоторых других тезисов, не уступающих тем, о которых я упомянул.

Что касается существования и природы того, что мы называем телом, то мы заблуждаемся еще более, чем Вы полагаете, и я согласен с Вами, что было бы нелегко доказать, что существует протяженность вне нас в том смысле, как ее обычно понимают. Но что касается духов иных, чем мы, то доказательство их существования возможно, причем их должно быть больше, нежели думают. Относительно

 

==307

бессмертия (perpetualite) всех духов, коль скоро они существуют, не может быть никаких возражений; однако немало затруднений связано с их началом, в том смысле, в каком его себе представляют.

Я нахожу также очень правильным то, что Вы говорите о простоте установлении Бога, который является причиной существования и некоторых частных зол; в противном случае Богу пришлось бы то и дело менять законы природы. Однако в этом пункте нужно кое-что добавить. Я припоминаю, как однажды я представил господам Арно и де Бийету небольшой диалог, который продвинул этот вопрос и не оставлял никаких сомнений относительно свободы, при условии, конечно, что в это понятие не будут вкладывать нелепый и противоречивый смысл. Quidquid agit, quatenus agit, liberum est ¹⁴. Следует также сказать, что Бог делает наибольшее из того, что он может, и обязан искать простые законы, для того чтобы найти место для всех вещей, сколько их можно поместить вместе; а если бы он пользовался другими законами, то вышло бы то же самое, как если бы для постройки дома пользовались круглыми камнями, которые требуют больше места, нежели они занимают.

Что касается души животных, то, мне думается, Вы могли бы решить этот вопрос совершенно по-иному, чем Декарт, если бы оценили собственную позицию так, как это делаю я; в этом я совершенно уверен, хотя исхожу из иных, нежели Ваши, доводов. Ибо те, которые Вы приводите в Ваших «Размышлениях», не кажутся мне достаточно убедительными и не приводят к тому, к чему должны были бы вести. Говорю это не из тщеславия и не из духа противоречия, но считаю необходимым отметить это, так как на долгом опыте убедился, что наши мысли до тех пор остаются смутными, пока мы не подкрепим их убедительными доказательствами. Вот почему я считаю, что можно было бы позволить себе рассуждать более вольно в математике, где вещи сами по себе упорядочены, но в метафизике рассуждать следует с большей строгостью, так как здесь мы лишены поддержки воображения и опытов и малейшая оплошность приводит к дурным следствиям, которые нелегко заметить.

Я думаю, то, за что Вы одобряете г-на Декарта и чего я не в состоянии оценить, происходит от того, что мы не вполне понимаем друг друга. Я считаю бесспорным, что приводимые им доказательства существования Бога не-

 

==308

удовлетворительны, ведь все, что он доказывает, — это только то, что мы обладаем идеей о Боге, или о самом великом из всех существ. Вы скажете, что иначе невозможно было бы рассуждать. Но ведь можно рассуждать и о самом большом из всех чисел, не впадая в противоречие, так же как и о самой большой из всех скоростей. Вот отчего требуется еще немало глубоких размышлений, чтобы довести до конца это доказательство. Но кто-нибудь мне скажет: я представляю себе наиболее совершенное из всех существ, потому что я представляю себе свое собственное несовершенство и несовершенство других несовершенных существ, хотя они, возможно, и совершеннее меня; я не мог бы этого сделать, если бы не знал, что такое абсолютно совершенное существо. Однако это возражение все-таки недостаточно убедительно. Ведь [с таким же правом] я могу утверждать, что двойка не является бесконечно совершенным числом, на том основании, что я имею в своем уме или могу воспринять идею другого, более совершенного числа, а сверх того и еще более совершенного, нежели это. Но в конце концов это означает лишь, что у меня нет вовсе никакой идеи бесконечного числа, хотя я и вижу, что всегда могу найти число, превосходящее данное число, каким бы оно ни было ¹⁵.

Различие души и тела полностью пока еще не доказано. Ибо поскольку Вы утверждаете, что мы не представляем себе отчетливо, что такое мысль, недостаточно того, что мы можем усомниться в существовании протяженности (т. е. той протяженности, которую мы отчетливо себе представляем), не сомневаясь в существовании мысли; этого, говорю я, недостаточно, чтобы решить, как далеко заходит различие того,что протяженно, и того, что мыслит, ибо могут сказать, что, возможно, различие между ними проводит наше неведение и что мысль заключает в себе протяженность каким-то неизвестным нам способом.

И все же я убежден в справедливости вышеупомянутых истин, невзирая на несовершенство обычных доказательств, вместо которых» я полагаю, можно выдвинуть строгие доказательства* Так как над этими вопросами я начал думать еще до того, как меня напичкали картезианскими суждениями, я сумел проникнуть в суть вещей через Другую дверь и открыл новые области; подобным: образом иностранцы, когда они путешествуют по Франции по маршруту, проложенному их предшественниками, не узнают почти ничего необычного, разве что ценой великой

 

==309

добросовестности или благодаря особому везению, тот же, кто едет по непроторенной дороге, даже с риском заблудиться, наверняка встретит нечто такое, о чем не подозревали другие путешественники.

Ваше сообщение о том, что здоровье г-на Арно полностью восстановилось, доставило мне большую радость. Дай Бог, чтобы он еще долго пребывал в добром здравии! Ибо где найдем мы другого такого человека? Прошу Вас передать ему мой нижайший поклон. Если г-н Би г в Париже, то передайте ему, пожалуйста, если Вы его увидите, что я огорчен известием о его болезни. Надеюсь, она пройдет, хочу, чтобы она никогда не возвращалась. Ибо в интересах общества беречь людей, которые могут быть столь полезны для него, как он. Что касается смерти бедного г-на Галине, то, признаюсь, эта утрата меня взволновала: он был сведущ во многих прекрасных вещах, и ему следовало бы передать издателю свою рукопись, прежде чем отправляться на Восток.

Хотелось бы, чтобы Ваш автор «Элементов», находящийся в Оратории [Иисуса], не забросил алгебру: у него к ней большие способности. Наверное, он не хочет больше ею заниматься, воображая, что все замечательное в этой области уже сделано, а остальное не стоит труда. Но я так не считаю, а у меня достаточно опыта для того, чтобы судить, сколько еще важного и прекрасного можно здесь совершить. Нередко мне приходилось решать такие задачи, которые требовали вычислений совсем иных, нежели обычные. Вы спросите: как можно найти исчисление иного рода? Я могу ответить на этот вопрос примером. Возьмем уравнение а² — b^y равно с и другое уравнение: d² — e^v равно /. Предположим, что <*-, Ъ, с, d, e,f суть величины известные, или данные; требуется найти два неизвестных: 2 и у. Подобная задача иногда может быть решена в числах... ^1в иногда при помощи линейки и циркуля, даже с помощью конических сечений или более сложных линий, а иногда и линий, которые я называю трансцендентными и которые неизвестны г-ну Декарту. Но оперировать такими вычислениями весьма трудно. Алгебра же несовершенна, если она не может справиться с этой задачей. Подумайте над ней, сударь, и попросите подумать автора «Элементов». Заканчиваю, примите заверения в моих чувствах и проч.

 

К оглавлению

==310

ЛЕЙБНИЦ — МАЛЬБРАНШУ

Ваше письмо я получил и был весьма обрадован свидетельством доброты, с коей Вы относитесь к человеку, чрезвычайно Вас почитающему. Мне ничего не известно об этом г-не аббате Кастеллане ¹⁸, который, должно быть, талантлив, поскольку, как Вы говорите, ему приписывают авторство «Христианских бесед», содержание которых настолько напоминает Ваши мысли, что я ни о ком другом, кроме Вас, не подумал. У меня нет сейчас под рукой этой книги, поэтому я не могу указать, в каком именно месте автор книги довольно прозрачно говорит, что она написана главным образом для картезианцев. Согласитесь, что, кто бы ни был этот молодой человек, если он напитался картезианским духом, он никогда не станет говорить как Эраст.

Мне хотелось бы отчетливо уразуметь причины, заставляющие Вас с такой убежденностью защищать те взгляды г-на Декарта, которые пока что не кажутся мне привлекательными. Поскольку я чрезвычайно высокого мнения о Вашем уме, я не доверяю себе самому, и, хотя у меня самого тоже имеются весьма убедительные, на мой взгляд, доводы, я боюсь, как бы мне не ошибиться, так как я еще не сумел построить на основании своих доводов строгое доказательство, что, по-моему, является абсолютно необходимым условием аргументированного рассуждения, особенно когда речь идет об отвлеченных материях. Поэтому я был бы Вам чрезвычайно обязан, если бы Вы смогли рассеять мои сомнения относительно следующих положений: во-первых, что материя и протяженность — это одно и то же; во-вторых, что дух может пребывать не связанным с каким-либо телом; в-третьих, что доказательства существования Бога, приводимые г-ном Декартом, удовлетворительны; в-четвертых, что вся истина зависит от воли Бога; в-пятых, что довод» который выдвигает г-н Декарт касательно соотношения преломлений, имеет силу; в-шестых, что в теле всегда сохраняется одно и то же количество движения. Я не хочу касаться его физической гипотезы, так как доказать ее можно, лишь объяснив явления природы. Не хочу также говорить о его радуге, хотя опыты г-на Ньютона заставляют усомниться, правильно ли г-н Декарт объяснил природу цветов. Что же касается магнита, то до тех пор, пока с помощью гипотезы г-на Декарта не откроют

 

==311

причину отклонений [магнитной стрелки], я не перестану сомневаться в том, что эта гипотеза хороша. Наиболее сведущие анатомы считают, что назначение шишковидной железы, [указанное Декартом], малоправдоподобно ^1Э, а движение, которое г-н Декарт приписывает сердцу и мышцам, опровергается опытом. Опыты с живым серебром ясно показывают, что г-н Декарт недостаточно объяснил причины метеоров. Назначение и главный признак истинной науки состоит, по моему мнению, в полезных изобретениях, которые можно сделать благодаря ей. Но я не вижу, чтобы хотя один картезианец изобрел что-нибудь полезное, пользуясь философией своего учителя, тогда как идеям Галилея мы обязаны по крайней мере введением маятников и так называемыми опытами с пустотой. Похоже, что никакой жатвы с философии Декарта нам не видать и все надежды погибли на корню со смертью ее создателя, так как большинство картезианцев — это всего лишь комментаторы. Хотел бы я, чтобы кто-нибудь из них оказался способным внести в физику столько, сколько Вы внесли в метафизику. Мало того, если бы вся физика Декарта оказалась правильной, то и тогда бы нее было бы мало проку. Ибо в конечном счете такими вещами, как первоэлемент и второй элемент, манипулировать трудно. Можно ли будет когда-нибудь отыскать и. и выполнить рецепт вроде следующего: Recipe lilram unam secundi elementi, unciam semis corporis ramosi, drachmae materiae subtilis, misce, fiat aurum? ²⁰ Думаю, понадобилась бы книга величиной с земной шар, чтобы объяснить, какое отношение может иметь какое-либо чувствительное тело к первоэлементам, даже если бы они существовали на самом деле и были познаны. Об этом можно судить по опытам с микроскопом. Ведь в одной капле воды имеется, вероятно, до 800000 мелких видимых животных, и каждое из них, можно сказать, еще так же далеко от первоэлементов, как далеки мы, так как и оно является телом и имеет много соответствий с обычными животными. Есть даже основания опасаться, что элементов вовсе не существует, так как фактически все дробится до бесконечности на органические тела. Если бы эти микроскопические животные в свою очередь оказались состоящими из животных или растений или тел, неоднородных до бесконечности, то очевидно, что никаких элементов не было бы. Все эти соображения, однако, не мешают мне высоко ценить г-на Декарта. Быть можете мало кто так ясно видит

 

==312

величие его ума, как я. Несомненно, что из всех авторов, живших до него и оставивших нам свои труды, с ним могут соперничать лишь Архимед и Галилей. Правда, лишь немногие мысли Архимеда дошли до нас, а что касается Галилея, то, хотя я нахожу, что, какую бы тему ему ни приходилось рассматривать, он всегда говорит нечто необыкновенное и можно только пожалеть о том, почему он не высказался подробнее, — тем не менее я должен сказать, что гений Галилея безусловно не был столь необъятен, как гений Декарта. Но зато он гораздо больше был привержен полезному и основательному, тогда как г-н Декарт, одержимый стремлением основать секту, увлекшись, наговорил немало, быть может, и остроумного но необоснованного и бесплодного. И все-таки я неизменно советовал бы всякому, кто любит истину, заняться углублением его системы, ибо на ней лежит отпечаток удивительного ума, а его физика при всей своей шаткости может служить образцом для истинной физики,, которой надлежит быть по крайней мере такою же ясной и последовательной, как его физика. Ведь и роман, если он достаточно хорош, может стать предметом подражания для историографа. Короче говоря: Галилей превосходен в искусстве превращения механики в науку; Декарт достоин удивления за умение объяснить при помощи блестящих догадок причины действий природы, и следовало бы пожелать, чтобы он больше занимался медициной, которая вся основана на догадках, хотя и необходима. Но Архимед, если верить тому, что сообщает о нем история, обладал талантом, которого нет ни у того, ни у другого: у него был великолепный дар изобретать машины,) полезные для жизни.

Геометрия есть то, что я менее всего ценю у г-на Декарта. Большая часть того, что он говорит по этому поводу, может быть без труда почерпнута из анализа Виста, и если Виет не воспользовался кривыми линиями помимо окружности, то лишь потому, что пребывал в убеждении, будто эти построения не являются геометрическими, ибо он несколько переоценивал заслуги древних. Достаточно исследовать внимательнее его труды, и можно понять, сколь много он был способен совершить в геометрии. Но в конце концов геометрия Виета и Декарта относится к тому, что мы можем сделать сегодня, так, как «Начала» Евклида относятся к Архимеду. Многое еще требуется, чтобы стало возможным свести все задачи к уравнениям.

 

==313

Например, надо найти кривую С (С} такого рода, чтобы,;

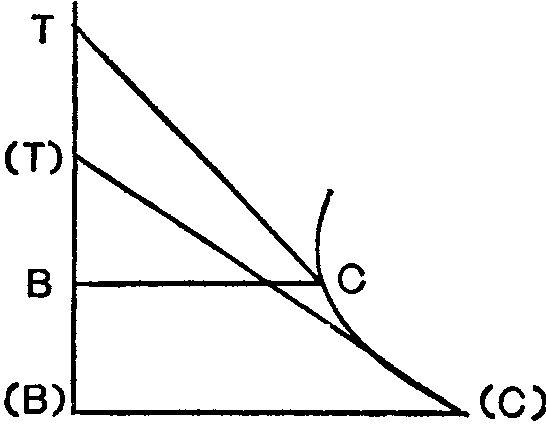
если провести из точки, взятой на кривой, С или (С), ординату СВ или {С) (В) и касательную СТ или (С) (Т) до оси Т (Т) В (В}, отрезок оси между ординатой и касательной, именно ТВ или (Г) (В}, был всегда равен той же прямой линии заданной величины А. Большинство наиболее красивых задач механики сводятся к таким геометрическим задачам, которые не являются ни плоскостными, ни кубическими, ни относящимися к сверхтелесному, но имеют совершенно иную природу.

Но если бы метафизика г-на Декарта была вполне доказана, я оценил бы ее бесконечно выше всего, что когда-либо смогут сделать в геометрии или механике. Искренне говорю: А

я предпочел бы добиться успеха в метафизике, чем найти клад. Ибо чего стоит все остальное в сравнении с Богом и душой. Да, я питаю поистине безмерную любовь к этой божественной науке и удивляюсь, видя, как мало ее уважают. Обыкновенно люди ценят что-нибудь одно: любители изящной литературы, правоведения, истории или коммерции не хотят слушать о реальных науках; физик или строитель машин смеется над скрупулезностью геометра, а геометры в свою очередь считают пустыми бреднями абстрактные рассуждения. Я же нахожу для себя необходимым равно ценить все истины соответственно тем следствиям, которые можно вывести из них, а так как нет ничего важнее и плодотворнее всеобщих истин метафизики, я люблю их сильнее, чем можно себе представить. Но мне бы хотелось видеть их доказанными с той же строгостью, какой придерживался Евклид в геометрии. И раз зашла об этом речь, я скажу Вам, сударь, все, что я нахожу нужным говорить о способе рассуждений г-на Декарта, когда он стремится излагать свои мысли в форме доказательства в конце своего ответа на третье возражение ²¹: здесь, на мой взгляд, они вкратце собраны все вместе. По поводу определений, которыми он пользуется, у меня есть следующее общее замечание: доказательства не могут быть точными, если нет уверен-

 

==314

ности в том, что определения, которые служат основанием для этих доказательств, возможны. Ибо если эти определения, или, коли угодно, эти определяемые вещи,; невозможны, тогда они будут заключать в себе противоречия, а если они заключают противоречия, из них можно вывести одновременно противоречивые следствия, и, значит, все доказательства, которые будут основаны на них, окажутся негодными: ведь может случиться, что противоречащее тому, что мы доказали, [также] не окажется истинным, поскольку основное правило (quod contradictor ia поп possint simul esse vera)²² имеет силу лишь применительно к возможным понятиям. Из этого видно, что определения ни в коем случае не являются произвольными, как думали многие.

Я ничего не говорю об определениях в частности: повод к этому представится в дальнейшем; незачем также исследовать здесь вопросы, ибо они не входят в доказательство, а служат лишь для подготовки ума. Перейду к аксиомам. Я нахожу, что 2-я аксиома (tempus praesens a proximo praecedenti non pendere etc.)²³ требует доказательства. Ведь коль скоро мы принимаем, что такая-то вещь существует, она не перестанет существовать без некоторой новой причины. О 4-й аксиоме — quicquid est perfectionis in re, est in prima ejus causa ²⁴ — можно сказать: лишь бы таковая [причина] существовала. Ибо если бы существовал прогресс причин до бесконечности, не было бы первопричины. Надо сказать, что это возражение не имело бы смысла, если бы была доказана 2-я аксиома. Некоторая неувязка имеется в отношении 7-й аксиомы: Res cogitans si norit cogitationes, quibus careat, eas sibi statim dabit si sint in sua potestate ²⁵. Тут необходимо добавить следующее ограничение: si noverit esse perfectiones ас in sua potestate esse, ac denique se illis carere ^2e. Правильность 9-й аксиомы зависит от 2-й, ш, следовательно, в ней тоже есть неувязка. По-видимому, 10-я аксиома грешит тем, что скрывает, так сказать, уловку, предполагая бесспорным, что необходимое существование и существование совершенное — это одно и то же. Перейдем теперь к самим доказательствам. Первое положение, или доказательство существования Бога, явно грешит против двух замечаний, только что нами сделанных, во-первых, потому что оно дает место уловке,; которую я отметил, говоря о 10-й аксиоме (где она использована), а во-вторых, потому что это доказательство

 

==315

 

использует определение Бога, чтобы доказать, что он существует, не доказав, что это определение возможно. Ибо нет уверенности в том, что понятие бесконечно совершенного существа не содержит противоречия аналогично таким понятиям, как motus celerrimus, numerus maximus ²⁷, и им подобным, которые решительно невозможны. Г-н Декарт в своем ответе на второе возражение articulo secundo ²⁸ признает аналогию inter Ens perfectissimum et Numerum maximum ²⁹, отрицая то, что это число влечет за собой числа. Впрочем, это нетрудно показать. Nam numerus maximus idem est cum numero omnium unitatum. Numerus autem omnium unitatum idem est cum numero omnium numerorum (nam quaelibet unitas addita prioribus novum semper numerum facit). Numerus autem omnium numerorum implicat, quod sic ostendo: Cuilibet numero datur respondens numerus par qui est ipsius duplus. Ergo numerus numerorum omnium non est major numero numerorum parium, id est totum non est majus parte ³⁰. Ответ, что наш ум, будучи конечным, не понимает бесконечного, неправилен, так как мы можем доказать и то, чего мы не понимаем. Во всяком случае, мы понимаем невозможность этого, ведь нельзя же говорить, что существует некое целое, которое не больше, чем его часть. Вы скажете, что идея совершенного существа имеется уже потому, что с тем же правом можно было бы утверждать, что имеется идея наибольшего числа и что о нем можно думать; однако мы видим, к чему это приводит. Разумеется, есть основания проводить различие между этими невозможными бесконечными, каковы число, движение и т. п., и абсолютно совершенным существом. Но для того чтобы убедиться в этом, необходимы новые и достаточно аргументированные рассуждения.

Второе положение, или доказательство существования Бога несовершенно... ³¹