Готфрид вильгельм лейбниц сочинения в четырех томах том 3

Вид материала

Документы

Содержание Париж последний день июля 1679 г. Лейбниц — мальбраншу Мальбранш — лейбницу К оглавлению Правило первое. Правило второе Правило третье.

Подобный материал:

• Готфрид вильгельм лейбниц сочинения в четырех томах том , 8259.23kb.
• Монадология, 209.43kb.
• Готфрид вильгельм лейбниц сочинения в четырех томах том, 9222.8kb.
• Лейбниц Г. В. Сочинения в четырех томах:, 241.84kb.
• Готфрид Вильгельм Лейбниц, 94.22kb.
• Лейбниц Готфрид Вильгельм (Leibniz Gottfried Wilhelm) немецкий ученый (философ, математик,, 271.47kb.
• Лейбниц (Leibniz) Готфрид Вильгельм (1646-1716), немецкий философ, математик, физик,, 201.35kb.
• Установочная лекция вткс, 212.41kb.
• Георг Фридрих Риман Готфрид Вильгельм Лейбниц литература, 208.32kb.
• Источник: Чехов А. П. Полное собрание сочинений и писем в тридцати томах. Сочинения, 565.43kb.

МАЛЬБРАШП — ЛЕЙБНИЦУ м

Париж последний день июля 1679 г.

Автор «Метафизических размышлений» — г-н аббат де Ланьон. Хотя он не поставил своего имени, он не скрывает этого. Мне это известно, так как он говорил об этом мне и некоторым другим лицам, с которыми я знаком.

 

==316

Так что, сударь, пожалуйста, не приписывайте мне это сочинение.

Немецкий дворянин ^3S уехал и, кажется, собирается навестить Вас. Говорят — хоть я и не верю этому, — что он нашел способ приведения к нулю всех членов уравнения, кроме первого и последнего. Хотя я уже давно совсем не занимаюсь исследованиями такого рода, мне все же хотелось бы знать, возможно ли это; не сомневаюсь, что Вам интересно будет проверить это, когда сей дворянин Вам об этом расскажет.

Автор «Элементов» убежден, что можно сделать еще немало открытий в анализе, однако теперь ему трудно вернуться к этому роду занятий. Все же я уговорил его пересмотреть свой труд, чтобы внести в него уточнения. Уже давно, сударь, мы ждем чего-либо на эту тему от Вас; несомненно, Вы можете... ³*

Г-н Бийет все еще болен малярией; месяца два назад он уже думал, что умирает. Вероятно, Вы знаете о том, что господа Арно и Николь больше не появляются в обществе: они скрылись. В чем тут дело; непонятно. Некоторые люди утверждают, что они отправились в Рим, но правда ли это, я не знаю ^а5.

У меня нет сведений ни о книгах, ни о новых открытиях, которыми я мог бы пополнить это письмо. Посему позвольте, сударь, заверить Вас и проч.

ЛЕЙБНИЦ — МАЛЬБРАНШУ

4 августа 1679 г.

Я ничего не знал об отъезде господ Арно и Николя и прошу Вас сообщить мне подробности об этом, если они

Вам известны.

«Христианские беседы» г-на аббата Катлана и «Метафизические размышления» г-на аббата Ланьона имеют так много общего с мыслями, высказанными Вами в «Разысканиях истины», что я вряд ли совершил большую ошибку, связав их с Вашим именем. Прошу Вас, расскажите мне подробнее об этих господах и особах подобного же дарования, так как знакомство с ними доставляет мне большую радость. Приятно, что умные и заслуженные люди посвящают себя занятиям метафизике ибо предстоит еще сделать немало важных открытий. Вы тонко

 

==317

оценили всю предварительную работу, которую я сделал в этой области.

Относительно корней уравнений вот мое мнение. Я полагаю, что решение всех уравнений геометрически, путем простого нахождения средних пропорциональных, невозможно, однако я не считаю невозможным выразить значение неизвестного в общем уравнении любой степени при помощи иррациональной формулы, наподобие корней Кардана, так как, по-моему, корни Кардана являются общими для кубического уравнения независимо от того„ что в выражение иногда входит мнимое число. Мне кажется, я уже высказывал Вам нечто в этом роде. Я различаю анализ, т. е. выражение значений, и геометрию, т. е. способы построения. Я говорю, что значение неизвестного найдено аналитически, если я могу его выразить целиком и только с помощью истинной формулы. Ибо даже если эта формула не всегда годится для построения, она все равно останется целью алгебры, которая отыскивает чистые значения, и к совершенному познанию искомого неизвестного (отвлекаясь от линий и от чисел) можно прийти лишь при условии, что получено это значение. Например: ж³ + рх равно q есть общее уравнение, корень которого х равен ^г |/ —?+Т/ -/ + 97 Р +

+ у -у- q — Т/ -, q² + у, Р³, что является истинным значением неизвестного во всех случаях, независимо от перемены знаков. И оно не может не быть корнем, поскольку всегда удовлетворяет уравнению.

Но чтобы доказать Вам это a priori, скажите, верно ли, что 2+—1+2— V—1 есть действительная величина? Без сомнения, это так, ибо она равняется 4. А куб величины 2+^:/—1 есть -{-2+11]/—1, следовательно, y+2+iiYi равен 2-t-^-/"^rrT. Однако У+2 - 11]/1 равен 2—-У—-1, следовательно, V +2 +11,]/"—1+

+Y+2— i\Y—1 равен 4. Таким образом, если бы корень Кардана дал Вам формулу х равен

V+2 +11 yi+V+2 - 11 V, Вы могли бы извлечь кубический корень из +2+11 Ч/—1 и получили бы

-j-2+V—1> а извлекая кубический корень из +2—

—i\.Y—1, получили бы -\-2—Y—1. Соединяя вместе

 



 

==318

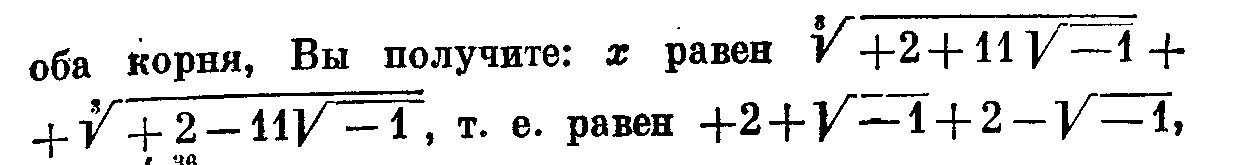оба корня, Вы получите: х равен Т+2+11—1+

-t-V+2-llV -1, т. е. равен -}-2+У1+2-У1, т. е. 4^м

Но для того чтобы извлекать кубический корень из

такого бинома, как 2 + 1Г — 1, правило Шотена, приводимое в конце его комментария, недостаточно. Требуется другое, и я его нашел: оно гораздо более общее и более красивое. Однако, если и невозможно извлечь корень из такого мнимого бинома, совокупная сумма корней

 

 



 

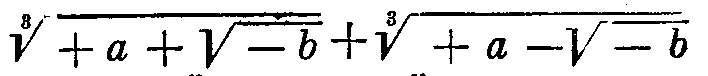
8/ ———————————" ' • З/——————————————-., обоих мнимых биномов V + а + У — Ь-тУ -\- а —у — Ь не перестает быть действительной величиной и уничтожение мнимого происходит на самом деле виртуально, хотя и невозможно продемонстрировать это в числах; зато мое правило извлечения убеждает в этом, по крайней мере для случая приближения сколь угодно точного.

Так как это вполне очевидно, Вы не сочтете странным, если я скажу Вам, что можно найти общие корни для [уравнений] высших степеней, например пятой степени. Действительно, в некоторых случаях я нашел такую возможность и могу дать иррациональные корни некоторых непонижаемых (indeprimable) уравнений пятой, седьмой, девятой степеней и т. д. до бесконечности. Тем самым я нашел безошибочный способ получения общих корней для какой бы то ни было степени. Но чтобы облегчить их вычисление, следовало бы составить предварительно некоторые таблицы, а я пока не имею времени этим заняться.

Все это я обдумал, еще когда был в Париже, где в то время находился и тот самый дворянин из Германии, о котором Вы слышали и которого я ставлю очень высоко. После этого он отправился в Италию, а затем вернулся в Париж; ему я сообщил мои результаты и побудил его развивать их дальше. Прежде он надеялся отыскать действительные корни для всех родов уравнений одной и той же степени, введенный в заблуждение нашими авторами, которые утверждали, что корни Кардана для [уравнений] третьей степени являются лишь частными корнями, Но я доказал ему, что на самом деле они являются общими и что для других случаев другие корни найти невозможно. С тех пор он много трудился и время от времени сообщал мне о своих успехах. Однако до сего времени он не сумел добиться решения уравнений пятой степени, о чем я сужу по весьма пространному письму, которое я получил от

 

==319

него недавно и на которое я ответил. Дело это сложнее,; чем думают. И все же я имею доказательство того, что оно может быть решено успешно. Но для этого нужно будет составить некоторые алгебраические таблицы, иначе придется делать слишком много вычислений. Таблицы, которые я задумал, могли бы служить великолепным подспорьем для всей алгебры. Однако довольно об этом. Мне хотелось бы знать, находится ли в Париже г-н герцог де Роанне и как поживает г-н де Бийет, которому я желаю доброго здоровья.

МАЛЬБРАНШ — ЛЕЙБНИЦУ

8 декабря 1692 г.

Сударь, один достойный человек оказал мне честь своим посещением и передал мне от Вашего имени некоторые заметки ³⁷, любезно сделанные Вами по поводу первых законов движения, изложенных в небольшом трактате, который я опубликовал ³⁸. Он обещал мне через 15 дней вернуться, чтобы получить мой ответ, не пожелав из скромности сообщить мне свое местонахождение. Итак, считаю своим долгом, сударь, поблагодарить Вас за лестную память обо мне и вместе с выражениями моего глубокого уважения обновить дружбу, коей Вы некогда почтили Вашего преданного слугу. Хотя за эти 15—20 лет, прошедших со времени Вашего пребывания в Париже, я не поддерживал с Вами связи по причине моих обычных обязанностей, я могу заверить Вас, что всегда следил с удовольствием за Вашими успехами, не раз просил г-на Фуше и г-на Тевено, недавно ушедшего от нас, передать Вам мои приветы, когда узнавал о том, что они собираются Вам писать, и вместе с ними питал радостную надежду вновь встретиться с Вами в Париже. Ибо кроме удовольствия повидать и обнять старого друга я рассчитывал поучиться у Вас тысяче полезных вещей, и прежде всего тем особым приемам, которыми надлежит пользоваться в интегральном и дифференциальном исчислении, а также способам его применения к вопросам физики. Особенно в интегральном исчислении у меня имеется много неясностей. Не могли бы Вы, сударь, изложить публике более подробно,, чем Вы это делали до сих пор, правила этого исчисления и способы его использования? Мне кажется, что Вас это касается больше, чем кого-либо,

 

К оглавлению

==320

не только потому, что Вас считают его изобретателем и никто, насколько я знаю, не оспаривает у Вас этой заслуги, но и потому, что Вы в совершенстве знаете математику ³⁹.

По поводу замечаний, которые Вы, сударь, сделали о первых законах движения, позвольте мне сказать Вам, что Вы не обратили внимания, как мне кажется, на сказанное мною вначале о том, что эти правила предназначены лишь для тех, кто принимает принцип, согласно которому во вселенной всегда сохраняется одно и то же количество движения. При таком допущении, я думаю, эти правила ⁴⁰ достаточно доказаны в небольшом трактате, хотя, быть может, я и был чересчур краток в некоторых местах. Мне кажется, что, коль скоро принят этот принцип,, попытки установить любые другие законы неизбежно приведут к какому-нибудь противоречию, в чем Вы легко убедитесь, если произведете расчеты. Но чтобы не оставлять Ваши замечания без ответа, я остановлюсь на тех, которые Вы, по-видимому, считаете основными.

Вы не считаете справедливым утверждение, что величина удара ни в коей степени не зависит от величины массы. «Можно было бы даже сказать, — пишете Вы, — что такое определение удара, в котором величина одного из данных тел вовсе не входит в значение результата, невозможно». В таком случае, сударь, прошу Вас принять во внимание, что тела лишь потому отталкиваются при ударе, что они непроницаемы; и следовательно, хотя масса величиной с Землю, ударяясь о песчинку, действует на эту песчинку со всей своей силой, если песчинка покоится на непоколебимом теле, тем не менее даже такая большая масса оттолкнет ее лишь по причине своей скорости,, если песчинка уступит [этому действию] без сопротивления. Ибо очевидно, что масса оттолкнет ее только потому, что песчинка непроницаема и что она придет с ней в соприкосновение; когда же вследствие своей скорости она приведет песчинку в движение, соприкосновение с ней прекратится.

По поводу неувязки, которую Вы находите в том, что бесконечно малое отличие данной величины совершенно меняет результат, я могу привести следующий пример: если т4 сталкивается с 4те, каждое из них должно отскочить так же, как оно приблизилось, но если тп4 превышает другое тело, на бесконечно малое количество силы, оно должно остаться в покое и передать все свое движе-,

 

==321

ние массе 4m. Это противоречит Вашему методу. И все же совершенно ясно, что это должно быть именно так в предположении, что движение не теряется, а тела являющего бесконечно твердыми. Ибо, если исходить из такого предполoжeния, тело не может в одно и то же время получить два противоположных движения в своих частях, что происходит с твердыми, но пружинящими телами, когда ударяемая часть отступает, в то время как часть, противостоящая ей, наступает, как я это и объяснил во вторых законах, которые ввиду этого обстоятельства значительно отличаются от первых. Так вот, если тело не может в одно и то же время получить два противоположных движения то ясно, что более слабое не может отдать нисколько от своего движения более сильному и его действие цели ком обратится на него самого. Я говорю целиком, так как предполагаю, что движение не теряется и действие всегда равно противодействию; это подтверждает и опыт. К тому же от4 толкает 4те в момент, который является моментом удара, следовательно, толкает его соответственно свое скорости, следовательно, со всей своей силой. Следовательно, хотя количественная разница бесконечно мала результат дает значительную разницу. Благоволите, сударь, дополнить Вашей вдумчивостью и Вашей принципиальностью краткость и неясность моего маленького трактата, и, я думаю, Вы согласитесь, что первые законы достаточно доказаны и предложить какие-либо иные просто невозможно, не впадая в противоречие, если, конечно исходить — как я это и делаю — из того, что движение не теряется. Впрочем, сударь, если я исходил из этого принципа, то потому, что он представлялся мне более соответствующим логике, нежели любой другой, и потом что все, что писали об этом в противоположном смысл, кажется мне неубедительным. Быть может, ошибаюсь я сам. Но как бы то ни было и как бы высоко я ни ценил моих друзей, я могу согласиться с ними лишь после того, как меня убедит очевидность их доводов, силу которых я и всегда чувствую: но это свойство моего характера, я думаю, не делает их менее достойными благожелательность. Следовало бы встретиться, чтобы приятно и с пользе побеседовать на эти темы, ибо нет ничего скучнее и тягостнее, чем философствовать в письмах, когда одолевали совершенно другие дела. Я по опыту знаю, как много времени обыкновенно уходит на это, да и Вы, сударь, тоже не располагаете свободным временем, расходуй

 

==322

3. Для того чтобы сформулировать законы, о которых идет речь, следует прежде всего определить силу удара способом, который сводится к следующему. Пусть а будет телом, которое не является самым маленьким из всех, а другое тело пусть будет Ъ. Скорость я пусть будет с, а скорость Ь пусть будет е. Удар пусть будет х. При этих условиях вот каково количество удара, которое позволяет познать эти первые законы.

4. Правило первое. Если ас не меньше, чем be, тогда т, будет произведением Ь, умноженного на сумму или разность с и е, а именно на сумму, когда эти скорости направлены в противоположные стороны, и на разность, когда они имеют одно и то же направление; иначе говоря, какое количество движения тела, не являющегося меньшим, в свою очередь не меньше, чем количество движения другого тела, удар будет равен произведению другого тела, умноженного на соответствующую скорость, или скорость, с которой тела сближаются.

5. Правило второе Если ас меньше, чем be, и скорости направлены в противоположные стороны, тогда х будет ас + be, т. е., если количество движения того тела, которое не является меньшим, меньше, чем количество противоположного движения другого тела, количество удара будет равно количеству общего движения.

6. Правило третье. Но если ас все еще меньше, чем be (как во втором правиле), а скорости направлены в одну сторону, тогда (как в первом) х будет произведением Ь на разность сие, иначе говоря, если количество движения того тела, которое не является меньшим, не есть меньшее (как в предыдущем правиле), а движения происходят в одном направлении, количество удара будет равняться (как в первом правиле) произведению тела, количество движения которого преобладает, умноженного на соответствующую скорость.

Замечания

7. По-видимому, невозможно свести все три правила к одному общему, хотя это было бы наиболее подходящим и, по-моему, может быть сделано либо уже сделано.

8. При сопоставлении всех правил кажется мало сообразным, что количество общего движения входит во второе правило и не входит в два других, а также то, что соответствующая скорость входит в первое и последнее правила

 

==324

и не входит во второе; напротив, кажется, что количество движения должно было бы входить всюду и соответствующая скорость — тоже всюду, и то и другое с определенными соответствующими различиями.

9. Кроме того, с удивлением приходится наблюдать, что отсутствует сходство в результате между 2-м и 3-м правилом, хотя они всегда наполовину согласуются между собой по исходным данным; между тем как в первом и последнем правилах данные согласуются наполовину либо вовсе не согласуются, способ же определения результатов всегда один и тот же, и это, по-видимому, противоречит главному правилу порядка, по которому datis ordinatis etiam quaesita esse ordinata et consentanea ⁴⁴.

10. Кажется странным также, что в первом и третьем правилах удар производится телом Ъ, умноженным на соответствующую скорость, и что это исключительное право производить удар безотносительно к величине другого тела никогда не предоставляется телу а, несмотря на то что оно обыкновенно является наибольшим. Однако с этой странностью можно было бы примириться, если бы она не служила источником следующей крупной ошибки.

11. Дело в том, что можно было бы даже сказать, что такое определение удара, в котором величина одного из данных тел вовсе не входит в значение результата, невозможно. Тем не менее это определение должно было бы иметь место согласно 1-му и 3-му правилам, где величина тела а не входит в значение удара х.

12. Некоторые найдут также странным и сочтут за большую несообразность то, к чему приводит первое правило, согласно которому то же тело Ь получит одинаковый удар и от тела а, которое равно ему, и от тела А, которое намного больше его, лишь бы только скорость А не превышала скорости а; но так как на с. 5 это возражение уже было предусмотрено, я ограничился тем, что предложил рассмотреть следующую неувязку. Пусть три тела будут равны Ъ, т и п, и пусть покоящееся тело Ь получит удар в одно и то же время и с одинаковой скоростью от те и от п. Если т ударяет так же, как т + п, значит, п не произведет ничего, а поскольку сказанное нет оснований относить к телу п с большим правом, чем к телу т, то, значит, они оба ничего не произведут, тогда как приходится утверждать, что вместе они производят больше, чем каждое в отдельности.

 

==325

13. Но особенно важно отметить, что первое правило не согласуется со вторым в случае, когда они должны совпадать, согласно рассуждению, которое я использую в «Новостях литературной республики» против законов движения г-на Декарта; в этом рассуждении я рассматриваю равенство как частный случай неравенства, в котором, 1 однако, разность бесконечно мала. С помощью этого приема я показываю, что два различных правила, которые, впрочем, относятся к разным случаям, должны одновременно иметь место в этом случае, когда они пересекаются или скрещиваются; но так как уравнение, которое я отсюда вывожу, не отвечает действительности и не является тождественным, это верный признак того, что правила сформулированы еще не совсем точно.

14. Согласно этому рассуждению, пусть ас равно i с;, а движения противоположны; согласно первому правилу, если ас равно be или превышает его на бесконечно малый избыток, удар будет Ьс + be; а согласно второму правилу, если Ьс тоже выше на бесконечно малый избыток, удар будет ас + be; следовательно, поскольку оба этих случая здесь равнозначны, be + be будет равно ас + be, что невозможно, за исключением того единственного случая, когда оба тела равны и, разумеется, равны и их скорости, поскольку здесь ас предполагается равным be.

15. Так как принципы реальной логики, или некоторого не зависящего от алгебры общего анализа, коими я воспользовался здесь, чтобы подвергнуть правила, или теоремы, испытанию a posteriori, не прибегая к опыту чувств, еще никогда доселе не применялись, я не удивляюсь тому, что такие выдающиеся мужи, как Декарт и автор «Разысканий истины», не приняли их во внимание. Если слг.аный этот автор даст им свое одобрение, их будут тем охотнее соблюдать впредь.