Высшее профессиональное образование т. Я. Дубнищева концепции современного естествознания

Вид материала

Документы

Содержание Закон сохранения и превращения энергии Первое начало термодинамики

Подобный материал:

• Учебно-методический комплекс концепции современного естествознания высшее профессиональное, 2306.3kb.
• Учебно-методический комплекс концепции современного естествознания высшее профессиональное, 2307.28kb.
• С. Г. Хорошавина концепции современного естествознания курс лекций, 6750.33kb.
• С. Г. Хорошавина концепции современного естествознания курс лекций, 5892.74kb.
• В. М. Найдыш Концепции современного естествознания, 8133.34kb.
• Учебно-методический комплекс дисциплины концепции современного естествознания Специальность, 187.08kb.
• Концепции Современного Естествознания, 274.86kb.
• Программа курса «Концепции современного естествознания», 168.05kb.
• Программа дисциплины Концепции современного естествознания Специальность/направление, 456.85kb.
• Бюллетень новых поступлений в нб согу за период с 05. 2011 по 10. 2011гг, 975.89kb.

4.2. Понятие «внутренняя энергия». Первое начало термодинамики

Закон сохранения и превращения энергии — один из основных законов, справедливых для неживой и живой природы. Важнейшее в нем — положение об эквивалентности теплоты и работы как разных форм энергии. Система изолированная не может обмениваться с окружающей средой ни веществом, ни энергией. Она большую часть времени находится в статическом состоянии, но эти условия почти не осуществимы. Если происходит обмен только энергией, систему называют замкнутой, а если энергией и веществом, — открытой. Существуют системы, помещенные в так называемую адиабатическую оболочку — это замкнутые системы, почти не обменивающиеся теплотой (например, закрытая крышкой кастрюля, термос). При равновесии ни одно из свойств системы не меняется со временем.

Функции состояния — величины, однозначно определяемые при равновесии. Нахождение этих функций и вычисление их изменений при переходе из одного состояния в другое входит в задачу термодинамики. Но абсолютные их значения не важны, и время как параметр в термодинамике не фигурирует. Фактически классическая равновесная термодинамика — это термостатика. Кроме того, в ней рассматриваются процессы, происходящие через последовательность равновесных состояний, т. е. обратимые. Да и равновесие в статическом состоянии соответствует смерти системы. Но она дает важные результаты, потому введем ее основные понятия и будем в дальнейшем путем формальных преобразований учитывать динамическую природу объектов и систем.

Полная энергия тела складывается из кинетической энергии движения тела как целого, из потенциальной энергии его во внешнем поле сил и внутренней энергии.

Внутренняя энергия — это обычно кинетическая энергия хаотического (теплового) движения его частиц и их взаимная потенциальная энергия. В последнюю включают и энергию колебательного движения атомов в молекулах, и внутриатомную энергию. В идеальном газе внутренняя энергия — энергия хаотического движения молекул. Понятие внутренней энергии относится к равновесным состояниям систем. Так как начальные и конечные состояния равновесны, на процессы, происходящие между ними, такого ограничения можно не накладывать.

Внутренней энергией системы U называют такую функцию состояния, приращение которой во всяком процессе, совершаемом системой в адиабатической оболочке, равно работе внешних сил над системой при переходе из начального состояния в конечное.

136

Под адиабатической оболочкой состояния меняются только путем изменения внешних параметров. И работа над системой в такой оболочке зависит не от способов перехода в состояние, а только от начального и конечного состояний. Для такой системы, перешедшей из состояния 1 в состояние 2, можно записать: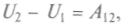причем работа внешних сил не зависит от вида пути. Внутренняя энергия U может быть положительной и отрицательной, как и работа внешних сил, и записанные соотношения нужно понимать алгебраически. Для квазистатических процессовт.е. 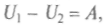можно записатьработа системы при адиабатических процессах совершается за счет убыли внутренней энергии.

Итак, внутренняя энергия есть функция параметров, определяющих состояние, т. е.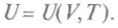Это уравнение называют калорическим уравнением состояния (в отличие от термического уравнения состояния типа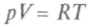для идеальных газов). Эти уравнения следуют из обобщения опыта.

Механическую теорию теплоты разрабатывал немецкий физик Р. Эмануэль, взявший себе имя Клаузиус (под которым и вошел в историю науки). Отметив, что между затраченной работой и полученной теплотой наблюдается постоянство соотношения только при процессах циклических (когда тело всегда возвращается в исходное состояние), Клаузиус ввел для уравнивания счета понятие внутренней энергии. И теплота, подводимая к воде, частично преобразуется во внутреннюю энергию расширения пара и воды, а частично — во внутреннюю энергию, которую пар возвращает при конденсации. Джоуль установил, что при рассеянии одинаковых количеств обеих энергий образуется одно и то же количество теплоты. Вслед за Джоулем, Томсоном и Гельмгольцем Клаузиус применил закон сохранения и превращения энергии к электрическим явлениям (1852): «Подобно тому как посредством теплоты может быть произведена механическая работа, так и электрический ток способен вызывать частично механическое действие, включая теплоту». У.Томсон применил этот закон к световым явлениям, химическим процессам и жизнедеятельности живых организмов, а затем — к электрическим и магнитным явлениям, установив выражение для энергии магнитного поля в виде интеграла, взятого по объему.

Молярная теплоемкость вещества определяется отношением количества теплоты, полученного одним молем вещества, к происходящему при этом увеличению температуры: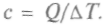Эта теплота расходуется на увеличение внутренней энергии вещества и совершение работы:Полная внутренняя энергия определяется кинетической энергией поступательного движения частиц: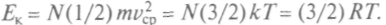Здесь R = = 8,31 Дж/(моль К), N — число молей.

Поэтому при изменении температуры меняется и внутренняя энергия.

137

Работа может быть совершена за счет расширения газа: Если газ находится в постоянном объеме, А = О и молярная теплоемкость определяется только изменением внутренней энергии и обозначается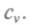Итак, = 12,6 ДжДмоль К).

Если при подводе теплоты газ имел возможность расширяться, можно вычислить работу при постоянном давлении. Из уравнения газового состояния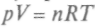видно, что увеличение температуры при постоянном давлении ведет к увеличению объема, т.е.



Совершаемая работа равна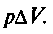Из первого начала термодина-

мики можно записать:



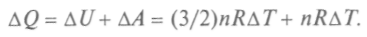
Для одного моля газа это означает, что 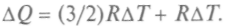Для молярной теплоемкости при постоянном давлении получаем значение: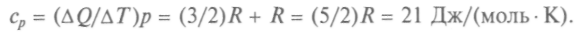



В рассматриваемой нами простой модели для газов все значения молярной теплоемкости должны быть равными, но теплоемкость при постоянном давлении больше теплоемкости при постоянном объеме на 8,4 ДжДмоль • К). Сравните с уравнением Майе-ра:

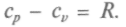
Если два атома как-то связаны, то они могут не только начать двигаться поступательно, но и вращаться вокруг общего центра масс. Поскольку каждый вид движения оттягивает на себя поступающую энергию, то изменение внутренней энергии за счет поступающей теплоты должно состоять из изменения энергии поступательного движения 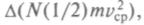вращения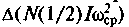и колебаний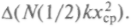При

поступательном движении двухатомной молекулы как целого возможно движение по трем равноправным направлениям, поэтому естественно предположить, что энергия делится поровну между этими тремя направлениями. При вращении молекулы, имеющей форму гантели, два направления являются равноценными — это направления, перпендикулярные оси вытянутости молекулы, на каждое из которых должна приходиться одинаковая энергия. При колебаниях (атомы связаны между собой чем-то вроде пружины) меняются потенциальная и кинетическая энергии, и на каждый тип колебания тоже приходится одинаковая энергия.

Молярная теплоемкость металлов имеет одинаковое значение, равное 25,2 ДжДмоль К) (закон Дюлонга и Пти). Это объясняется тремя степенями свободы колебаний каждого атома около своего положения равновесия в кристаллической решетке, причем на каждую приходится вдвое больше энергии, чем на поступательные (одна — на кинетическую энергию и одна — на потенци-

138

альную). Зависимость теплоемкости от температуры, несколько отличающуюся для разных металлов, не способна объяснить классическая теория. Кроме того, исходя из значения молярной теплоемкости, непонятно, почему электронный газ, переносящий энергию в металле, не получает тепловой энергии. Или он переносит энергию, обеспечивая теплопроводность и электропроводность, но сам энергии не поглощает?! Загадкой оказывается и огромная теплоемкость воды, в три раза большая теплоемкости металлов. Все эти нерешаемые в классической теории вопросы говорят о более сложной структуре веществ, чем эта примитивная модель.

Закон сохранения и превращения энергии в середине XIX в. приобрел права всеобщего закона природы, объединяющего живую и неживую природу. Его кратко формулируют так: «Энергия сохраняется», или: «Тепло, полученное системой, идет на приращение ее внутренней энергии и на производство внешней работы». Сохраняется именно энергия, а не теплота. Понятие энергии позволило рассматривать все явления природы и процессы с единой точки зрения, объединить все явления. Впервые в науке абстрактное понятие заняло центральное место, оно пришло вместо ньютоновой силы, соответствующей чему-то осязаемому, наглядному, конкретному, хотя и облаченному Ньютоном в математические одежды.

Понятие «энергия» прочно вошло в нашу жизнь. Под энергией чаще всего понимают способность тела совершать работу. Лорд Кельвин признал, что силы могут исчезать и возникать, а энергия не уничтожается. Это понятие соответствовало и его религиозным взглядам: он считал, что Творец в самый момент творения мира наделил его запасом энергии, и этот божественный дар будет существовать вечно, тогда как эфемерные силы подвержены многим превратностям, и с их помощью в мире ткется ткань явлений преходящих.

Первое начало термодинамики, связанное с законом сохранения и превращения энергии, акцентирует внимание на внутренней энергии: приращение внутренней энергии при переходе системы из одного состояния в другое складывается из суммы работы внешних сил над системой и количества теплоты, получаемого системой. Оно требует сохранения энергии изолированной системы, но не указывает направления, в котором процессы могут происходить в природе. Это направление указывается вторым началом. Кроме того, второе начало вводит температурную шкалу, не связанную с рабочим веществом термометра и его устройством. Два начала позволяют установить множество точных количественных соотношений между различными макроскопическими параметрами тел в состояниях термодинамического равновесия или около него.

139

4.3. Преобразование тепловой энергии в механическую работу

Исследовать работоспособность тепловых машин решил молодой французский инженер Н.С.Карно. Его работа «Размышление о движущей силе огня и о машинах, способных развивать эту силу» (1824), в которой он сформулировал общий и абстрактный методы решения специальной задачи, вышла за пределы специального исследования, положив начало новой науке — термодинамике.

Анализируя механизм действия тепловых машин, Карно исходил из того, что для их работы нужно наличие разности температури затем их выравнивание, так же, как для работы водяных машин необходима разность уровней воды. Поэтому «возникновение движущей силы обязано в паровых машинах не действительной трате теплорода, а переходу его от горячего тела к холодному, т.е. восстановлению его равновесия». Но определяет ли производимую машиной работу? Ведь возможен процесс выравнивания температур без всякой работы, как при непосредственном тепловом контакте. Для того чтобы работа производилась, нужен посредник, рабочее вещество, которое было бы способно отобрать теплоту у нагревателя (более горячего тела) при более высокой температуре и отдать ее холодильнику (более холодному телу) — при более низкой.

Карно рассмотрел идеальную машину, которая имела бы большую эффективность, чем любая реальная машина. Идеальна она потому, что в ней отсутствует внутреннее трение, а процесс характеризуется только двумя температурами.

Теорема Карно, доказанная в этой работе: эффективность любой тепловой машины, работающей при температурах причем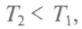меньше эффективности идеальной машины. Кар-

но не вычислял коэффициент полезного действия (КПД), но указал, что он пропорционален разности падения температур единицы теплорода:

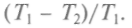
Идеи Карно в течение 10 лет не вызывали интереса, пока Клапейрон не выпустил свою книгу (1834), в которой он дал анализ работы Карно, перевел ее на математический язык и несколько улучшил сам цикл Карно — заменил его другим, теперь общеизвестным циклом из двух адиабат и двух изотерм, называемый циклом Карно. Клапейрон впервые употребил графическое изображение обратимых круговых процессов и вычислил работу как соответствующую площадь на графике.

Превращение теплоты в работу для практических целей важно, как и превращение одного вида энергии в другой. Обратимся к схеме работы тепловой машины. В цилиндре машины помещается при атмосферном давлении вещество (газ), называемое рабочим телом. Повысим его температуру, не меняя давление, и газ должен расшириться. Поршень пере-

140

местится на расстояние х, причем он будет двигаться против внешнего давления атмосферы. Если площадь поршня равна s, то совершается работа против силы, равной ps, так как р — сила, приходящаяся на единицу площади. Поршень переместился на расстояние х, и работа на этом пути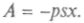Здесь поставлен знак минус, так как работа совершается

газом, который отдает ее внешней среде, перемещаясь в направлении, противоположном приложенной силе. Поскольку произведение sx есть изменение объема газаи равна теплоте,

затраченной на нагревание газа.

Пусть газ под поршнем в цилиндре находится в равновесии с окружающей средой. Будем медленно выдвигать поршень из цилиндра, не нарушая равновесия в каждый данный момент и сохраняя постоянство температуры. Этот процесс соответствует эмпирическому закону Бой-ля — Мариотта: pV= const. Точка 7, представляющая состояние газа, перейдет на плоскости р, V — в точку 2. Если опять же медленно и при постоянной температуре сжимать газ, то точка 2 вернется в точку 1, потому что изотермический процесс обратим. Существует и другой обратимый процесс в идеально теплоизолированном сосуде — адиабатический. Этот процесс тоже очень медленный, так что температура во время сжатия или расширения выравнивается во всех точках, но меняется в зависимости от объема:

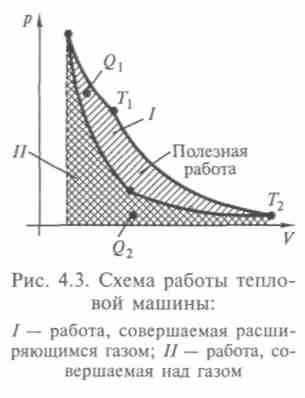
Оба этих обратимых процесса, конечно, идеализированы, реальные процессы могут только приближаться к ним, поскольку всегда есть какие-то потери теплоты на теплоизоляцию, вязкость среды и т. п. Цикл Карно состоит из двух изотермических и двух адиабатических процессов, которые образуют на графике в координатах (р, V) криволинейный четырехугольник. Адиабаты идут круче изотерм, поэтому они образуют боковые линии, а изотермы — основания. Теплота подводится и отнимается при изотермическом процессе, поэтому верхняя изотерма отвечает расширению газа в тепловом контакте с нагревателем температуры Т₁, а нижняя — сжатию при контакте с холодильником при температуре Т₂. Пусть газ получает от нагревателя теплоту Q₁, а холодильнику отдает теплоту Q₂. Тогда за весь цикл он получит теплоту Q = Q₁ - Q₂, равную совершенной работе А. Отношение работы А к теплоте, полученной у нагревателя (с нагревателем связаны основные затраты, ведь это ему нужно топливо), называется коэффициентом полезного действия теплового двигателя: КПД =

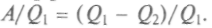
Коэффициент полезного действия двигателя, таким образом, определяется разностью температур нагревателя и холодильника, деленной на температуру нагревателя:

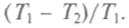
На рис. 4.3 графически представлена совершенная работа при Q = А + Q₁, Возможность построения машины без холодильника, т.е. с КПД = 1, которая могла бы превращать в работу всю теплоту, заимствованную у теплового резервуара, не противоречит закону сохранения энергии. По своему практическому значению она

141




не уступала бы перпетуум-мобиле, так как могла бы производить работу за счет почти неисчерпаемых запасов внутренней энергии, содержащихся в воде морей и океанов, в атмосфере и недрах Земли. Такую машину У.Оствальд назвал перпетуум-мобиле второго рода (в отличие от перпетуум-мобиле первого рода — вечного двигателя, производящего работу из ничего). Карно исходил из идеи невозможности вечного двигателя, опираясь на факты многочисленных опытов, которая была возведена в постулат, названный вторым началом термодинамики.

На основе термодинамики У. Томсон (впоследствии лорд Кельвин) предложил абсолютную шкалу температур (см. рис. 4.1). Он исходил из того, что КПД всех обратимых двигателей определяется только абсолютными температурами холодильника и нагревателя. Машина Карно может использоваться для градуировки шкалы, если закрепить точку таяния льда. Проведя цикл Карно между данным телом и тающим льдом и измерив соответствующие количества теплоты, можно из прямой пропорциональности количества теплоты и температур найти абсолютную температуру (в К). С 1954 г., по определению X Генеральной конференции по мерам и весам, температура тройной точки воды (точка равновесного сосуществования льда, воды и пара) считается равной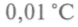(273,16 К) при давлении 6,09 гПа.

Можно ли повысить КПД за счет уменьшения температуры холодильника? Казалось бы КПД = 1 при Т₂ = 0, но все газы гораздо раньше начинают сжижаться, т. е. перестают быть газами, следовательно, абсолютный нуль температур недостижим. Это и составляет содержание третьего начала термодинамики, утверждающего, что нельзя охладить вещества до температуры абсолютного нуля посредством конечного числа шагов. Понимание этого начала требует представлений об атомном строении вещества, тогда как другие начала есть обобщение непосредственного опыта и не зависят ни от каких предположений. Но: можно ли повысить КПД за счет увеличения температуры нагревателя? По этому пути развивается вся теплотехника (плазменные двигатели, например, имеют температуру горячего вещества до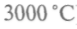), но этим путем

повышение КПД происходит медленней, чем понижением Т₂. А когда хотят понизить температуру холодильника, обычно забывают, что на это надо затратить работу хотя бы с помощью жид-

142

кого воздуха. В холодильных установках теплота отбирается от холодного тела и отдается горячему, но только за счет работы извне. Смысл второго начала термодинамики в том и состоит, что нельзя непрерывно получать работу, не имея резервуара энергии. Для Земли таким источником энергии является Солнце. На солнечной энергии работают и гидростанции, и солнечные батареи, и ветряные двигатели. Их работа не противоречит второму началу термодинамики. В 1851 г. Кельвин сформулировал второе начало иначе: «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара». Близкую формулировку дал Макс Планк: «Невозможно построить периодически действующую машину, единственным результатом которой было бы поднятие груза за счет охлаждения теплового резервуара». Поэтому иногда говорят: «Процесс Томсона — Планка невозможен». Клаузиус выдвинул второй постулат в таком виде: «Теплота не может самопроизвольно переходить от тела менее нагретого к телу более нагретому». Можно показать, что все эти варианты второго начала эквивалентны и вытекают один из другого.