Высшее профессиональное образование т. Я. Дубнищева концепции современного естествознания

Вид материала

Содержание

4.7. Основные положения молекулярно-кинетической теории и эмпирические газовые законы
4.8. Связь параметров газа с его микроструктурой. Распределение Максвелла

Подобный материал:

1 ... 12 13 14 15 16 17 18 19 ... 53

4.6. Микро- и макропеременные в описании систем. Основные модели

Идеал научной теории, сложившийся под влиянием успехов классической механики, состоял в отыскании наиболее общих, количественно формулируемых законов природы. В механике состояние системы однозначно определяют координаты и скорости частиц; по ним можно вычислить любую величину в данный момент времени: энергию, момент импульса и пр. Знание действующих на систему сил позволяет определить состояние сиc-

151

темы в любой другой момент времени. Эта удивительная однозначность и детерминизм — основы классического динамического описания.

Параллельно с развитием классической механики частиц и твердых тел шло развитие и механики сплошных сред (жидкостей, газов и деформируемых твердых тел). Трудами Бернулли, Эйлера и других ученых были заложены основы гидродинамики идеальной жидкости. Уравнение Эйлера для движения жидкостей и газов в отсутствие вязкости и теплопроводности можно вывести из законов Ньютона для системы материальных точек. Вместо координат и импульсов частиц Эйлер задавал состояния системы некоторыми функциями, описывающими распределение различных физических величин в пространстве (плотность, давление и скорость); они связаны не с отдельной частицей, а с точкой пространства в данный момент времени, т. е. описывают состояние среды в целом. И для решения задач нужно задавать не конечное число координат и импульсов, а начальные и граничные условия на них. Если уравнение Эйлера решать вместе с уравнением непрерывности, выражающим закон сохранения вещества в гидродинамике, решаются любые задачи динамики идеальных сред, т. е. динамический характер законов динамики идеальных сред остался незыблемым.

Гидродинамика неидеальной (вязкой) жидкости стала развиваться в XIX в. При движении такой жидкости (или газа) возникают силы трения и теплообмен. Имеет место диссипация энергии, которая не учитывается в идеальных моделях. В этом случае уже нельзя строить теорию процессов, опирающуюся только на механику, где все процессы обратимы. И такая теория была построена только на основе теории теплоты, где иначе (чем в механике) определяется состояние системы.

Состояние системы в термодинамике зависит от ее параметров — температуры Т, давления р, объема V. Если последние два параметра имеют механический смысл, то первый его лишен. Между параметрами существует связь, выражаемая уравнением состояния, которое устанавливается из опыта и не получено теоретически. Известно, что состояние для заданной массы газа в отсутствие внешних воздействий не меняется, если газ находится в равновесном состоянии.

Газ — это совокупность слабосвязанных частиц. Атомы в газах находятся на значительном расстоянии друг от друга и обладают свободой движения, хаотически сталкиваясь друг с другом и со стенками сосуда. Расстояния между атомами столь велики по сравнению с их размерами, а время сближения частиц столь мало, что все газы ведут себя одинаково.

Модель идеального газа — это газ, молекулы которого пренебрежимо малы, свободно двигаются и сталкиваются по законам упругого удара. Частицы принимаются за материальные точки,

152

взаимодействующие на расстоянии. Частицы газа являют собой наилучший пример неупорядоченной совокупности однородных объектов (фр. gaz, греч. chaos — хаос).

Модель реального газа, предложенная Ван-дер-Ваальсом (1873), отличалась от модели идеального газа учетом объема самих молекул и их взаимодействия. Последний фактор несколько уменьшает давление — каждая молекула при столкновении как бы тормозится притяжением соседних. Так появилось новое уравнение состояния, которое получило имя автора.

При низких абсолютных температурах газы уже не похожи на газы, их свойства определяются квантовыми законами. В этих условиях используют квантовые функции распределения, которые переходят в классические с повышением температуры. Области, в которых наступают отклонения от закона распределения, называют областями вырождения газа (для водорода, например, эта область находится при Т = 1 К, для других газов — еще ниже).

4.7. Основные положения молекулярно-кинетической теории и эмпирические газовые законы

Тела могут находиться в разных агрегатных состояниях (газообразном, жидком, твердом или в виде плазмы), но все они состоят из молекул, а молекулы — из атомов. Элементарная молекулярно-кинетическая теория газов основана на классической механике, молекулы представлены материальными точками.

Молекулярно -кинетическая теория строения вещества основана на следующих основных положениях:

Молекулярное строение веществ подтверждено существованием процессов растворения, диффузии, броуновского движения и др.
Молекулы находятся на определенных расстояниях друг от друга, что доказывается возможностью сжатия и перечисленными выше процессами. Размеры молекул газа малы по сравнению с расстояниями между ними. При отсутствии внешних сил молекулы газа равномерно заполняют весь предоставленный им объем.
Молекулы связаны силами молекулярного взаимодействия — притяжения и отталкивания. Силы отталкивания на малых расстояниях превосходят силы притяжения, но быстро убывают с увеличением расстояния между молекулами, и с некоторого расстояния r₀, называемого радиусом молекулярного действия, ими можно пренебречь. В отсутствие внешних воздействий молекулы находятся в устойчивом состоянии на расстояниях 2r₀. Эти силы имеют электромагнитную природу.
Молекулы находятся в непрерывном беспорядочном движении, что доказывают те же процессы.

153

Внутреннюю энергию молекулярной системы составляет сумма кинетической энергии движения молекул, потенциальной энергии их взаимодействия и всех прочих энергий этой системы.
В любом, даже самом малом объеме газа, к которому применимы выводы этой теории, число молекул велико.

Газовые законы были получены эмпирически для равновесного состояния:

закон Бойля—Мариотта, который выполняется при постоянной температуре Т, имеет для 1 моля идеального газа следующий вид:

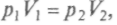т. е. описывается изотермой на pV- диаграмме;

закон Гей-Люссака — изменение объема при температуре Т, постоянном давлении

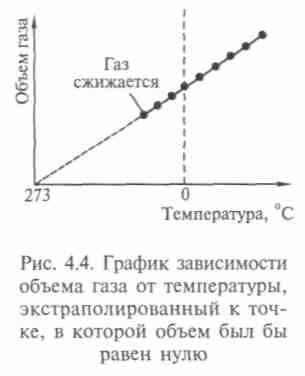
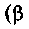— коэффициент объемного расширения газа):

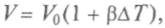т.е. описываемом изобарой (рис. 4.4);

закон Шарля - изменение давления и температуры T при постоянном объеме

т.е. изохорный процесс. Здесь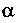

— термический коэффициент давления.

Уравнение состояния, введенное Клапейроном, для заданной массы газа объединяет три газовых закона, связывая между собой параметры газа. Клапейрон впервые употребил и графическое изображение обратимых циклических процессов, вычислив работу как соответствующую площадь на графике. Согласно закону Авогадро, количества любых газов при одинаковых температуре и давлении занимают одинаковый объем, который при нормальных условиях равен 22,4 л = 22,4 • 10^-3 м³. Д. И. Менделеев обобщил с учетом закона Авогадро уравнение Клапейрона: pV= 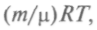где m — масса газа; μ — его молекулярная масса; R — универсальная газовая постоянная, равная 8,31 Дж/(мольК).

Газовые законы, как всякие эмпирические, справедливы приблизительно и описывают поведение почти идеальных газов при невысоких давлениях и не слишком высоких температурах. Подобных универсальных законов нет для жидкостей или твердых тел. Их свойства зависят от типа частиц, из которых они состоят, и силы взаимодействия между частицами в них меняются в широких пределах. Опыт показывает, что эти силы, имеющие отчасти характер электростатического взаимодействия, при расстояниях между молекулами более 10^-9 м убывают столь быстро, что ими можно пренебречь. Поэтому свойства идеальных газов близки к свойствам реального газа.

154

Так как молекул много и они часто ударяются о стенку, их суммарное действие на поверхность можно заменить одной непрерывно действующей силой, которая как бы сглаживает отдельные толчки. Такое описание называется статистическим — время и место удара каждой молекулы о поверхность не интересны, важен только общий эффект, т. е. то, что входит в статистический закон.

Средняя кинетическая энергия поступательного движения молекулы газа при тепловом равновесии одинакова для всех молекул газов, находящихся в тепловом контакте. Значит,

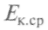обладает основным свойством температуры и не зависит от внутренней структуры молекул. И ее можно принять за меру температуры газа или тела, находящегося в тепловом контакте с газом: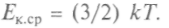

Температура газа должна определяться средней кинетической энергией его молекул. В 1730 г. Д. Бернулли наметил кинетику газовых сред. В частности, он сумел из атомистических представлений вывести закон Бойля — Мариотта. Этот закон вывел и М. В.Ломоносов — его гипотеза о внутреннем вращательном движении составляющих материю частиц позволила наглядно объяснить механизм нагревания двух трущихся друг о друга поверхностей.

4.8. Связь параметров газа с его микроструктурой. Распределение Максвелла

Процесс — это переход системы из одного состояния в другое через некоторую последовательность промежуточных состояний. Важной схематизацией, часто используемой в молекулярной физике, является понятие о равновесном процессе.

Равновесным называют состояние, если характеризующие его параметры при отсутствии внешних воздействий постоянны неограниченное время, иначе — состояние неравновесное. Равновесное состояние изображается точкой в координатной плоскости, если по осям отложить значения каких-либо двух параметров системы. Неравновесное состояние так изобразить нельзя, так как параметры имеют неопределенные значения. Процесс перехода системы из одного равновесного состояния в другое всегда связан с нарушением равновесия системы. Но если это происходит медленно, то за любой малый промежуток времени состояние системы можно охарактеризовать определенными значениями параметров. И такой процесс можно считать состоящим из ряда равновесных процессов. Равновесный процесс состоит из непрерывной последовательности равновесных состояний, и чем медленнее протекает процесс, тем он больше похож на равновесный. Только равновесный процесс можно изобразить непрерывной линией на графике.

155

Рассматривая газ как совокупность мельчайших упругих шариков — атомов, которые хаотично двигаются в пустоте, А.Крениг из вероятностных соображений принял, что атомы газа движутся по трем взаимно перпендикулярным направлениям с одинаковой скоростью. Элементарный расчет дал уравнение, связывающее давление р и объем V газа с его массой т и скоростью атомов

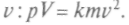Кре-

ниг в 1856 г. верно указал на связь pV с кинетической энергией частиц, получил из кинетической модели закон Авогадро и объяснил охлаждение газа при адиабатическом (хотя при оценке давления он взял коэффициент 1/6 вместо 1/3). Работа Кренига подтолкнула Клаузиуса к опубликованию своих результатов (1857). Рассматривая удар молекул о стенку по законам упругих столкновений, Клаузиус вывел:

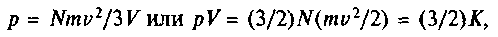
где К — энергия поступательного движения всех частиц газа. Поскольку давление и объем идеального газа связаны уравнением Клапейрона, он получил:

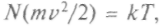здесь k — постоянная

Больцмана.

Кинетическая теория объяснила многие явления — теплопроводность, диффузию, растворение и др., позволила рассчитать сначала относительные и абсолютные значения средних скоростей молекул разных газов, найти средний свободный пробег молекулы — среднее значение длины прямолинейного пути, проходимого молекулой между последовательными соударениями. Его дал Дж. Максвелл в 1866 г.

Отсюда нетрудно посчитать и с р е д н е е число соударен и й частицы за определенное время. При обычных условиях оно велико — около 5 млрд соударений за 1 с. Подведение теплоты увеличивает кинетическую энергию движения частиц, растут давление и температура. Как только они достигают высоких значений, возрастает вероятность столкновений между частицами, и сходство газов исчезает.

Поступающая в газ энергия должна как-то распределиться между атомами. Но одна часть атомов движется быстрее, другая — медленнее, а их средняя кинетическая энергия пропорциональна температуре газа Т. Если к сосудам, содержащим равное число молекул двух разных газов, подвести равное количество теплоты, то их температура повысится на одну и ту же величину, т.е. удельные теплоемкости с, приходящиеся на одну молекулу, одинаковы.

156

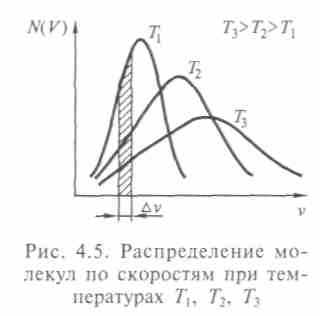
Распределение молекул по скоростям определяет распределение энергий, или энергетический спектр газа, от которого зависят многие свойства газов. В состоянии равновесия все направления скоростей равновероятны, иначе тепловое движение частиц не было бы беспорядочным, но равными по величине они быть не могут. Если такое и случится, то столкновения быстро изменят эту ситуацию. Максвелл рассуждал следующим образом: ни одно направление движения и ни одно значение скорости не являются выделенным, и предоставленный самому себе газ приходит в стационарное состояние с определенным распределением скоростей (рис. 4.5).

Поскольку по всем трем осям проекции скоростей должны быть независимы и равновероятны, можно записать

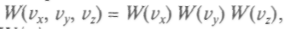
причем все вероятности распределения

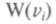должны иметь одинако-

вый вид. Кроме того, с одинаковой вероятностью будут встречаться скорости вдоль каждой оси и против нее, т. е. вероятность должна зависеть от квадрата скоростей

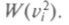Повернем теперь координатные оси так, чтобы новая ось

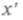совпала с направлением вектора скорости, т. е. проекции скорости в новой системе будут

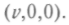От поворота осей значение

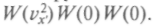функции

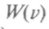измениться не должно, поэтому

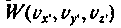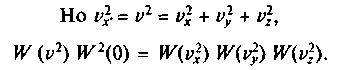
Таким образом, нужно найти функцию от суммы величин, которая распадается на произведение таких же функций от каждого слагаемого в отдельности. Этим свойством обладает только показательная функция. Например, для основания степени числа

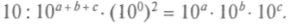(Можно взять и любое другое число.) Но квадраты проекций скорости на оси — величины размерные и потому не могут стоять в показателе степени без коэффициента, обеспечивающего его безразмерность.

Среднее значение кинетической энергии имеет размерность квадрата скорости:

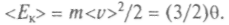Поэтому величина

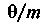имеет ту же размерность, а обратная ей

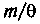— размерность обратного квадрата скорости. Если взять за основу величину е = 2,718..., то среднее значение кинетической энергии не изменится и согласуется с прежним определением. Тогда искомая функция

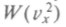окажется пропорциональной

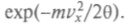Очевидно, что нужно подобрать еще коэффициент пропорциональности, исходя из условия, что W = 1. Запишем этот коэффициент в готовом виде и получим искомое максвеллово распределение по скоростям: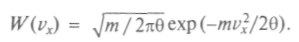

Можно показать, что никакая другая функция распределения, кроме

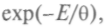не совместима с законом сохранения энергии при отдельных соударениях частиц. Графически

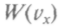представляется гауссовой кривой. Максимум этой кривой лежит в ок-

157

рестности нуля, т.е. в газе больше всего молекул с нулевыми значениями компонент скорости. Это связано с равной вероятностью направлений скоростей, так что средняя проекция скорости хаотического движения на любое направление равна нулю. Гауссовы распределения встречаются в разных системах (даже в социальных). Площадь под кривой соответствует общему числу молекул газа.

Максвелл рассматривал свою модель газа как математическую аналогию реальности. «Вместо того, чтобы говорить, что все частицы тверды, упруги и шарообразны, можно сказать, что частицы являются центрами сил, действие которых ощутимо лишь на некотором малом расстоянии, где они проявляются внезапно и в виде очень интенсивной силы отталкивания». Далее он проводит сопоставление с величинами, характеризующими тепловое движение, заменяя среднюю скорость распределением скоростей (1859). Проведя ряд опытов, Максвелл заключил, что сила отталкивания должна быть обратно пропорциональна пятой степени расстояния между молекулами. В 1866 г. он вывел свой закон распределения по скоростям уже с этой поправкой.

Распределением Максвелла называется распределение молекул по проекции скорости, определяемое функцией

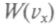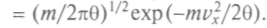Распределение по компонентам скорости является частным случаем нормального закона распределения Гаусса, которому подчиняются случайные ошибки при измерениях.

Абсолютное значение скорости не может быть отрицательным, и функция распределения по абсолютному значению скорости начинается с ее нулевого значения:

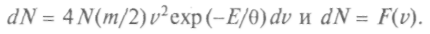
Основное отличие от предыдущего распределения заключается в существовании множителя — квадрата скорости.

Поскольку

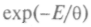при возрастании скорости убывает быстрее, чем

возрастает квадрат скорости, получающееся распределение асимметрично. Максимум функции F(v) имеет место при наиболее вероятной скорости

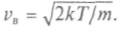Среднее арифметическое значение скорости находится по формуле:

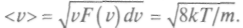Среднее значение квадрата скорости равно

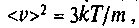а квадратный корень из него называют средней квадратичной скоростью:

Распределению Максвелла удовлетворяют закон сохранения энергии и принцип детального равновесия в отдельных соударениях, когда при хаотическом движении в газе скомпенсированы два противоположно направленных процесса с равными скоростями. Этот принцип справедлив не только для газов, но и для любых систем в состоянии полного хаоса.

158

Blog

Высшее профессиональное образование т. Я. Дубнищева концепции современного естествознания

Содержание