Высшее профессиональное образование т. Я. Дубнищева концепции современного естествознания
| Вид материала | Документы |
СодержаниеГармонические колебания 3.7. Распространение звука в средах и реакция организма на звуковые волны Р — мощность, излучаемая колеблющейся пластинкой в направлении х. I связана с давлением p |
- Учебно-методический комплекс концепции современного естествознания высшее профессиональное, 2306.3kb.
- Учебно-методический комплекс концепции современного естествознания высшее профессиональное, 2307.28kb.
- С. Г. Хорошавина концепции современного естествознания курс лекций, 6750.33kb.
- С. Г. Хорошавина концепции современного естествознания курс лекций, 5892.74kb.
- В. М. Найдыш Концепции современного естествознания, 8133.34kb.
- Учебно-методический комплекс дисциплины концепции современного естествознания Специальность, 187.08kb.
- Концепции Современного Естествознания, 274.86kb.
- Программа курса «Концепции современного естествознания», 168.05kb.
- Программа дисциплины Концепции современного естествознания Специальность/направление, 456.85kb.
- Бюллетень новых поступлений в нб согу за период с 05. 2011 по 10. 2011гг, 975.89kb.
Современный мир полон волн: волны звука, распространяющиеся в воздухе и других средах; переменный ток, используемый в быту и технике; волны механических колебаний в струнах, колебания в кристаллах кварца, используемые для стабилизации частот
108
радиопередатчика или в часах; волнение и зыбь в озерах, прудах и океанах; волны землетрясений, изучаемые в сейсмологии; электромагнитные волны, которые в оптическом и радиодиапазонах используют для передачи информации; волны вероятности, которые в мире квантов описывают поведение микрочастиц и более сложных форм вещества.
Механические колебания — это периодические движения. Чаще всего они возникают при нарушении устойчивого состояния равновесия системы, при этом равнодействующая сил не равна нулю. Одна из сил должна зависеть от времени, и система должна обладать избыточной энергией. За период колебаний выполняется закон сохранения и превращения энергии. Колебания могут происходить при наличии упругих сил, силы тяжести; электрические колебания (напряжений и сил токов) происходят в электрических цепях. Несмотря на разную природу колебаний, в них обнаруживаются общие закономерности. Физическая система, совершающая колебания, называется осциллятором.
Колебания массы, прикрепленной одним концом к пружине, простой пример гармонического движения. Математический маятник состоит из точечной массы, подвешенной на невесомой и нерастяжимой нити. При малой амплитуде почти каждый колебательный процесс можно считать линейным (рис. 3.3).
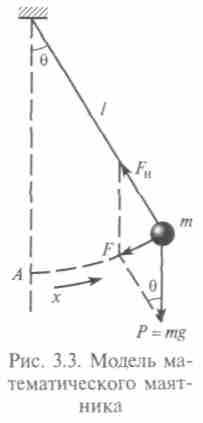
Период колебаний маятника при малых амплитудах, как установил еще Галилей, определяется его длиной и не зависит от массы маятника. Период колебания маятников разной длины l пропорционален квадратному корню из их длин
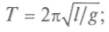 пружины — обратно пропорционален собственной частоте колебаний
пружины — обратно пропорционален собственной частоте колебаний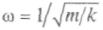 (k — жесткость пружины). Это свойство изохронности колебаний маятника использовалось в XVII в. для отсчета равных промежутков времени, но колебания затухали, приходилось маятник подталкивать, и не было автоматического счета числа колебаний. Гюйгенс применил маятник в своих часах в качестве регулятора и довел их до практического использования и коммерческого успеха. Восемнадцатое столетие даже получило наименование века часов, хотя тогда они использовались, в основном, для определения долготы места.
(k — жесткость пружины). Это свойство изохронности колебаний маятника использовалось в XVII в. для отсчета равных промежутков времени, но колебания затухали, приходилось маятник подталкивать, и не было автоматического счета числа колебаний. Гюйгенс применил маятник в своих часах в качестве регулятора и довел их до практического использования и коммерческого успеха. Восемнадцатое столетие даже получило наименование века часов, хотя тогда они использовались, в основном, для определения долготы места.Если сместить тело массой т, прикрепленное к пружине, то со стороны пружины на него будет действовать возвращающая сила, направленная в сторону, противоположную силе, вызвавшей смещение (будем считать, что трение отсутствует). Для небольших смещений х возвращающая сила F= -kx. Используя второй закон Ньютона, можно записать: F=mW= -kx, откуда ускорение
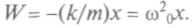
109


 Это выражение — основной закон простого гармонического колебания: ускорение материальной точки математического маятника пропорционально смещению.
Это выражение — основной закон простого гармонического колебания: ускорение материальной точки математического маятника пропорционально смещению.На языке колебаний и волн наиболее ясно предстает единство природы. Гармонические колебания описываются функцией, изменяющейся по закону синуса или косинуса:
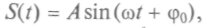 где
где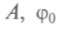 - постоянные величины; А — амплитуда колебаний,
- постоянные величины; А — амплитуда колебаний,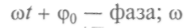 — круговая частота
— круговая частота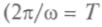 — период колеба-
— период колеба-ний; 1/Т = v — частота). Если амплитуда со временем убывает, то колебания называются затухающими; если колебания происходят под действием внешней, периодически изменяющейся силы, их называют вынужденными; если же колебания происходят после выведения системы из состояния равновесия, то это — свободные колебания. Колебания могут иметь разную природу, но они обладают общими чертами и подчиняются общим закономерностям, что позволяет единым образом рассматривать механические, электрические и другие колебания. Колебания классифицируют по способу возбуждения (собственные, вынужденные, параметрические и автоколебания), по зависимости изменяющейся величины от времени и пр. С точки зрения кинематики различают периодические и непериодические колебания.
Всякая система, совершающая колебания, обладает своими свойствами, которым соответствуют собственные колебания, а им — собственные частоты. Если на систему подействовать периодически меняющейся силой, то система откликнется малыми колебаниями, частота которых будет совпадать с частотой вынуждающей силы. Если частота этой силы совпадет с одной из собственных частот системы, то амплитуды колебаний резко возрастут. Такое явление называется резонансом. Резонанс имеет место при настройке радиоприемника на частоту передающей станции. В нелинейных системах, содержащих источник энергии, могут возникать незатухающие колебания и без внешнего воздействия — это автоколебания.
Любое повторяющееся движение можно рассматривать как результат сложения простых гармонических колебаний, а любое волновое движение — как сумму простых гармонических волн. Этот тезис, доказанный (1822) французским математиком и физиком Ж. Б. Фурье, служит основой для изучения повторяющихся явлений в самых разных областях. Волновые свойства света и микрочастиц лежат в основе современной картины мира. Гармоническое колебание играет значительную роль при изучении любых колебаний (особенно в акустике и оптике).
Волны — это изменение состояния среды, распространяющееся в ней без переноса вещества и несущее с собой энергию и импульс. Энергия, импульс и скорость — важнейшие характеристики волн. Процесс распространения колебаний (волна) может
110
быть описан в общем виде математически. Основные свойства волн можно изучить на простых примерах и сформулировать общие положения, которые будут справедливы для любого типа волн.
Морские волны бьются о берега, при штормах ворочают огромные камни и переворачивают корабли. Телецентр излучает волны мощностью в десятки тысяч ватт, малую долю которых улавливают телевизоры. Волны переносят энергию любой величины от одной точки к другой, распространяясь с конечной скоростью, зависящей от среды их распространения: так, световые волны распространяются со скоростью 300 000 км/с, звуковые (в воздухе) — 344 м/с. Электромагнитные волны, приходящие на Землю от Солнца, имеют плотность мощности порядка 1 кВт/м2 в широком диапазоне длин волн; эта энергия преобразуется зелеными растениями в химическую. При сжигании дерева или угля эта энергия вновь высвобождается. Наличие импульса у электромагнитных волн менее заметно, но оно было даже измерено П.Н.Лебедевым (1912). Существуют проекты использования светового давления на огромные паруса для передвижения в Солнечной системе.
Монохроматической называют волну от гармонического источника. Если колебания происходят по гармоническому закону, при распространении от источника до точки на расстоянии z волна приходит с некоторым запаздыванием, связанным с конечной скоростью распространения волны:
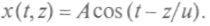 Волновой фронт — геометрическое место точек, колеблющихся в одной фазе. Он отделяет область пространства, вовлеченную в волновой процесс, от той, где колебания еще не возникли. В зависимости от волновой поверхности волны могут быть плоскими или сферическими. В плоской волне амплитуда постоянна, а в сферической — убывает обратно пропорционально квадрату расстояния от источника.
Волновой фронт — геометрическое место точек, колеблющихся в одной фазе. Он отделяет область пространства, вовлеченную в волновой процесс, от той, где колебания еще не возникли. В зависимости от волновой поверхности волны могут быть плоскими или сферическими. В плоской волне амплитуда постоянна, а в сферической — убывает обратно пропорционально квадрату расстояния от источника.Если тело участвует в нескольких волновых движениях, то эти движения складываются в одно. Волновое движение образуется, если колеблющихся частиц много и они связаны между собой. Каждая испытывает влияние возвращающих сил, поэтому сами частицы или части пружины больших перемещений не совершают, но вдоль пружины распространяется импульс. Следя за перемещением импульса, проходящего расстояние dx за время dt, можно ввести его скорость как v = dx/dt. При не очень больших возмущениях среды волновое движение подчиняется принципу суперпозиции — два импульса распространяются независимо. Если два импульса проходят через пружину и друг через друга, смещение пружины оказывается равным алгебраической сумме отдельных смещений. Импульсы гасят друг друга в момент встречи (если имеют противоположные знаки) или складываются (при одинаковом направлении распространения).
Бегущая волна образуется следующим образом. Пусть один конец пружины или струны закреплен и ни одна точка не испытывает смещений, а ко второму концу приложена сила, которая
111

 начинает в момент времени t = 0 поднимать и опускать его. При распространении этого воздействия на соседние участки по струне или пружине побежит волна со скоростью
начинает в момент времени t = 0 поднимать и опускать его. При распространении этого воздействия на соседние участки по струне или пружине побежит волна со скоростью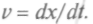 Расстояние х,
Расстояние х,которое данный участок волны проходит за время t, равно vt. Период T возбуждающего колебания и будет периодом волны, за время T волна распространяется на расстояние, называемое длиной волны
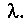 Тогда скорость волны
Тогда скорость волны Отсюда
Отсюда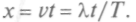
Амплитуда волны меняется по закону:
 Из
Извыражения для скорости волны получаем:
 Зависимость
Зависимостьамплитуды волны от координаты в любой момент времени имеет вид:
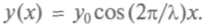
В поперечных волнах частицы перемещаются перпендикулярно направлению распространения волны. Смещение среды может также вызвать импульс, распространяющийся перпендикулярно к нему. Такой эффект наблюдают, когда резким боковым движением посылали импульс вдоль веревки. В электромагнитных волнах направления электрического и магнитного полей перпендикулярны направлению распространения волны.
В продольных волнах частицы перемещаются вдоль направления распространения волны, например, распространение звука в воздухе или волн сжатия—растяжения в самой пружине. В звуковых волнах плотность газа, где распространяется звуковая волна, меняется по закону синуса.
В твердых телах распространяются продольные волны, в случае неоднородной плотности могут распространяться и поперечные. Стоячая волна (рис. 3.4) возникает, если у струны закрепить оба конца. Импульс будет отражаться от обоих концов, распространяясь по струне. Так как расстояния между импульсами
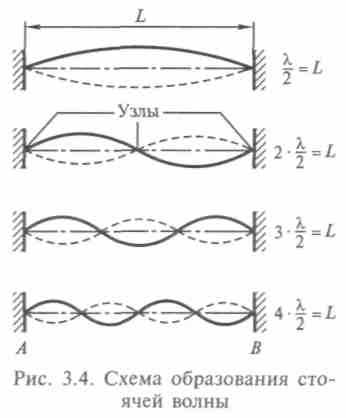
одинаковы, процесс будет повторяться. Если первоначальный импульс — синусоидальный и оба импульса равны по амплитуде, распространяются в разные стороны, смещение в точке поворота меняет знак, можно получить также синусоидальную волну, форма которой между двумя закрепленными точками остается неизменной, а амплитуда меняется со временем. Точки, в которых смещений нет, называют узлами, а точки максимального отклонения вниз или вверх — пучностями стоячей волны. На струне длиной L можно возбу-
112
дить стоячие волны, даже если ее узлы приходятся на точки закрепления струны:
 .... На соседних участках колебания противоположны по фазе. Стоячие волны на струне можно представить и как результат сложения двух бегущих волн. При наложении друг на друга они создадут весьма устойчивую картину.
.... На соседних участках колебания противоположны по фазе. Стоячие волны на струне можно представить и как результат сложения двух бегущих волн. При наложении друг на друга они создадут весьма устойчивую картину.Понятие стоячих волн, зародившееся в науке о звуковых колебаниях, распространилось и на другие колебательные системы, благодаря чему была решена задача теплового излучения, приведшая к созданию квантовой гипотезы. С использованием этой модели и волновой механики сумели описать строение атома. В современной теории атом рассматривается как система, обладающая определенными формами стоячих волн с характеристическими частотами. Вместо орбит в модели атома Бора теперь вводят замкнутые кольца стоячих волн. Чем дальше орбита, тем большее число пучностей должно войти в это кольцо. По тому же принципу строятся модели для атомного ядра. Волны — это не просто участки струны, отклоняющиеся вверх и вниз, и даже не колеблющиеся электроны, а мера вероятности того, что частица находится в данном месте.
Поверхностные волны распространяются по поверхности раздела сред. Волны на поверхности воды сопровождают перемещение судов. Если создать возмущение на поверхности воды, то возникнут волны. Частицы жидкости, находящиеся вблизи впадины, при создании возмущения будут стремиться заполнить ее под действием тяжести, создавая волны в воде. Частицы волны будут двигаться почти по окружностям, т. е. как бы совмещая свойства продольных и поперечных волн, но отличаясь от них обеих. Радиусы окружностей с глубиной уменьшаются до нуля. Скорость распространения волны с зависит от X: для длинных волн — пропорциональна
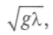 для коротких
для коротких а для средней длины — от всех перечисленных параметров (здесь р — плотность жидкости,
а для средней длины — от всех перечисленных параметров (здесь р — плотность жидкости,  — коэффициент поверхностного натяжения). Значит, длинные волны вызваны силой тяжести, а короткие — силой поверхностного натяжения. Если длина волны меньше глубины водоема, то вблизи дна наблюдается чисто продольное движение, а на поверхности и вблизи нее каждая частица воды движется по эллипсу (комбинации колебаний в двух направлениях).
— коэффициент поверхностного натяжения). Значит, длинные волны вызваны силой тяжести, а короткие — силой поверхностного натяжения. Если длина волны меньше глубины водоема, то вблизи дна наблюдается чисто продольное движение, а на поверхности и вблизи нее каждая частица воды движется по эллипсу (комбинации колебаний в двух направлениях).Необычную волну — уединенную — наблюдал в 1834 г. шотландский ученый Дж. Рассел. Баржу тянули по каналу; после неожиданной остановки приведенная ею в движение масса воды остановилась около носа баржи, а затем оторвалась от него. И это уединенное возмущение покатилось по каналу с большой скоростью, не меняя формы. Рассел заметил, что не меняется и скорость С этой уединенной волны, она зависит от глубины канала h и высоты волны
 Кроме того, одна большая
Кроме того, одна большаяволна может распадаться на несколько волн, которые проходят
113


 одна через другую, подобно малым волнам на поверхности. Многие отнеслись критически к открытым Расселом свойствам уединенной волны.
одна через другую, подобно малым волнам на поверхности. Многие отнеслись критически к открытым Расселом свойствам уединенной волны.Уравнение для описания длинных волн на воде вывели датские ученые Д.Д. Кортевег и Г. де Фрис (1895). Их уравнение, известное по имени авторов как уравнение КдФ, является дифференциальным уравнением в частных производных и годится для описания самых разных нелинейных волн. Если скорость линейных волн зависит от длины волны и не зависит от амплитуды, то для нелинейных волн существенны обе зависимости. Точное решение имеется лишь для волн в ряде случаев. Нелинейные волны начал изучать еще великий немецкий математик Георг Риман. Нелинейность проявляется при «опрокидывании» набегающих волн, которую можно наблюдать на речной отмели или в прибое на берегу моря. При нарастании крутизны волны может образоваться волна в виде ступеньки, которую называют бором. Бор — один из примеров ударной волны. Другие примеры ударных волн — взрывной звук, слышимый, когда реактивный самолет проходит звуковой барьер или когда пастух щелкает бичом. Ударные волны в воздухе — явление сложное; на фронте ударной волны скачком растут давление, плотность, температура, и значения этих скачков столь велики, что происходит яркое свечение (например, при ядерном взрыве, при падении метеоров-болидов).
Уравнение КдФ, после того как стали разрабатывать методы его решения на ЭВМ, используется для описания ионно-звуковых волн в плазме, волн возбуждения в живой материи, дислокаций в кристалле, распространения сверхкоротких световых импульсов в оптических средах и др. На его основе разработаны методы решения дифференциальных уравнений в частных производных (так называемый метод обратной задачи рассеяния).
При исследовании сложения двух уединенных волн оказалось, что высокие уединенные волны движутся скорее, так как после взаимодействия волн сохраняются их форма и скорость, процесс похож на упругое столкновение двух частиц. Такую волну назвали солитоном (от англ. solitary — уединенный). И солитоны в самом деле ведут себя как частицы. При соприкосновении таких волн большая замедляется и уменьшается, а малая ускоряется и увеличивается. И далее — по циклу, подобно упругим мячам. Результатом взаимодействия солитонов может быть лишь сдвиг фаз. Океанические солитоны (цунами, «девятый вал») могут возникать не только на поверхности, но и в глубинах, тогда из-за неоднородностей среды они образуют «групповые солитоны» (смерчи или торнадо). В нелинейной оптике наблюдается эффект самоиндуцированной прозрачности, эти солитоны естественно использовать для передачи информации по оптическим волокнам. Механизм усиления солитонов похож на явление комбинационного рассеяния света.
Аналогичный механизм распространения имеет и «элементарная частица мысли» — нервный импульс. Было установлено, что по нерву распространяется не электрический ток, а некоторая электрохимическая реакция, порождающая бегущий импульс напряжения. При этом передний фронт импульса не расплывается, т. к. диффузия ионов через мем-
114
брану носит нелинейный характер — подавляет малые отклонения от нормального состояния и усиливает большие. Огромное количество вихрей — это тоже солитоноподобные образования.
3.7. Распространение звука в средах и реакция организма на звуковые волны
Звуковыми называют упругие волны, вызывающие у человека ощущение звука. Среди них различают: тоны или музыкальные звуки; шумы; звуковые удары. Гармонический процесс — это чистый или простой тон, а ангармонический — сложный тон. Сложный тон раскладывают на простые, при этом наименьшая частота — основной тон, а обертоны или гармоники имеют частоты, кратные основному. Набор частот с указанием интенсивно-стей компонент называют акустическим спектром. Шум — это звук со сложной неповторяющейся временной зависимостью: согласные звуки речи, скрип, шорох, вибрации машин. Звуковой удар — это кратковременное звуковое воздействие: взрыв, хлопок и др.
Колеблющаяся плоская пластинка возбуждает в среде бегущую волну с амплитудой
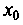 и частотой
и частотой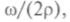 распространяющуюся от источника,
распространяющуюся от источника,и передает слою воздуха массой
 некоторую энергию.
некоторую энергию.Максимальная кинетическая энергия этого слоя

 — плотность слоя воздуха. Но при простом гармоническом движении средняя потенциальная энергия равна средней кинетической, и это выражение описывает запас энергии в слое площадью А и толщиной
— плотность слоя воздуха. Но при простом гармоническом движении средняя потенциальная энергия равна средней кинетической, и это выражение описывает запас энергии в слое площадью А и толщиной Пусть колебания начинаются при t = 0 и распространяются в воздухе со скоростью
Пусть колебания начинаются при t = 0 и распространяются в воздухе со скоростью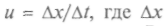 — расстояние, на которое распространится возмущение за время At. Разделив выражение
— расстояние, на которое распространится возмущение за время At. Разделив выражениедля энергии на
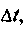 получим:
получим: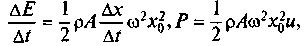 где Р —
где Р —мощность, излучаемая колеблющейся пластинкой в направлении х. Зная мощность, приходящуюся на единицу площади, вычисляют интенсивность любой бегущей волны, т. е. и звука. Выражение для интенсивности звука
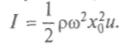 получим, разделив обе части этого выражения для мощности на А:
получим, разделив обе части этого выражения для мощности на А:Итак, интенсивность звуковой волны пропорциональна квадрату амплитуды и определяется как скорость потока энергии через единичное поперечное сечение. Наименьшая интенсивность звука, которую слышит человеческое ухо, порядка I0 = 10-12 Вт/м2, ее называют порогом слышимости.
Реактивный самолет, набирающий высоту недалеко от человека, создает интенсивность звука в 1015 раз, а поезд метро - в 1010 раз большую. Болевой порог интенсивности — 1012I0, это значе-
115


 ние может достигаться на концертах рок-музыки. Приведенные показатели степени, умноженные на 10, определяют децибель-ную шкалу интенсивности звука, названную в честь Генриха Белла. Интенсивность звука в децибелах
ние может достигаться на концертах рок-музыки. Приведенные показатели степени, умноженные на 10, определяют децибель-ную шкалу интенсивности звука, названную в честь Генриха Белла. Интенсивность звука в децибелах и обозначается дБ. Тогда порог слышимости составляет 0 дБ, а концерт рок-музыки — 120 дБ. Санитарная норма соответствует 30 — 40 дБ.
и обозначается дБ. Тогда порог слышимости составляет 0 дБ, а концерт рок-музыки — 120 дБ. Санитарная норма соответствует 30 — 40 дБ.Шумовая болезнь проявляется в повышенном артериальном давлении, быстрой утомляемости, плохом сне и ослабевании слуха. Тембр звука при одинаковых громкости и высоте тона определяется спектральным составом звука, испускаемого разными источниками. Звуковые волны распространяются в воздухе со скоростью около 330 м/с при нормальных условиях, причем их скорость не зависит от частоты.
Человеческое ухо способно воспринимать только часть звуковых колебаний, которые, попадая на барабанную перепонку, возбуждают нервную реакцию. Для оценки интенсивности звука удобнее использовать звуковое давление, возникающее в среде при прохождении звука.
Интенсивность звука I связана с давлением p, плотностью среды
 и скоростью звука с соотношением:
и скоростью звука с соотношением: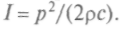 Высота звука определяется частотой колебаний: она тем выше, чем больше частота. Интервалу волн длиной от 20 м до 1,6 см, воспринимаемых ухом, соответствует диапазон частот между 16 и 20 000 Гц соответственно. Звуковые частоты и соответствующие им длины волн (Гц/м) приведены ниже:
Высота звука определяется частотой колебаний: она тем выше, чем больше частота. Интервалу волн длиной от 20 м до 1,6 см, воспринимаемых ухом, соответствует диапазон частот между 16 и 20 000 Гц соответственно. Звуковые частоты и соответствующие им длины волн (Гц/м) приведены ниже:
Указанные пределы слышимости относятся к молодым людям. С возрастом диапазон сокращается, мужчины начинают утрачивать чувствительность к высоким нотам раньше, чем женщины. В среднем возрасте они уже не воспринимают звуки выше 12 000 Гц, а после 50 лет верхняя часть спектра звуков оказывается недоступна. Интересно, что воспринимаемый нами диапазон звуков шире того, который используется для речи или пения (100—1000 Гц). Но когда высокие частоты гаснут (как правило, в недорогих акустических системах), то теряются яркость и красота звучания, а если низкие частоты, звук кажется монотонным, хотя высота тона воспринимается верно.
Уже у античных авторов можно найти указания на то, что звук обусловлен колебательным движением (Птолемей, Евклид). Аристотель отметил, что скорость звука имеет конечную величину, причем не одинаковую для низких и высоких тонов. Он представлял этот процесс так: «Звук происходит оттого, что звучащее тело определенным образом приводит воздух в движение, который при этом сжимается и растягивается
116
и ударами звучащего тела проталкивается все дальше и дальше, отчего звук и распространяется во все стороны».
С XVII в. начались попытки определения скорости звука. Скорость распространения упругих продольных волн совпадает со скоростью распространения импульса, сообщенного одному концу упругого стержня. Продольные волны в стальной проволоке плотностью 8 г/см3 и с модулем упругости 2,06 107 Н/м2 должны иметь скорость распространения 5 • 1000 м/с. При этом она не зависит ни от амплитуды, ни от частоты колебаний, пока упругие деформации подчиняются закону Гука.
Громким пением какой-либо ноты над открытым музыкальным инструментом можно возбудить стоячую волну основной моды в струне, частота которой соответствует взятой высоте тона, и затем услышать, как струна звучанием отзывается на голос, пока в ней не затухла стоячая волна.
Замечательную связь между числами и законами музыкальной гармонии открыл еще Пифагор. Он использовал монохорд — струну, закрепленную на одном конце и перекинутую через острие ножа, так что к ней можно было подвешивать гири, создавая различные натяжения. Тогда было известно и об ощущениях, вызываемых разными комбинациями тонов: одни были приятными, другие — диссонирующими. Пифагор доказал, что приятные сочетания создают струны с одинаковым натяжением, длины которых находятся в отношении 2:1, два таких тона отличаются на интервал в одну октаву. Интервал 3 :2 получил название квинты. Он отметил, что приятные сочетания связаны с простыми числами, характеризующими отношение длин.
Таким образом, высота тона закрепленной струны связана с ее длиной. Для одной и той же струны, колеблющейся с одной, двумя, тремя и более пучностями, частоты колебаний находятся в пропорции 1: 2: 3 и т.д. Уменьшение длины струны в 2 раза приводит к повышению тона рождаемого ею звука на октаву. На основании подобных закономерностей Пифагор разработал теорию музыкальной гаммы и гармонии. Пифагор и его последователи — пифагорейцы — верили, что в основе природы лежат математические закономерности. По законам гармонии строилась и их космологическая система.
Идею о выделении в любом сложном колебании основного тона и гармоник выдвинул Г. Гельмгольц (1862). Звучание любого инструмента определяется пропорциями гармоник. Из-за гармоник звук флейты отличен от звука скрипки, хотя колебания воздуха в трубе, флейте или органе одни и те же. Правда, колокольчики не образуют простой ряд целых чисел, поэтому их звучание не столь мелодично. Еще из опытов с маятниками поняли, что сущность музыкального звука в его периодичности. Галилей заметил, что осциллятор резонирует на действие периодической силы, когда ее частота совпадет с собственной частотой маят-
117

 ника, определяемой его длиной. Он соорудил простую систему — погрузил бокал почти по самый край в сосуд с водой и, слегка ударяя по краю, извлекал из бокала звуки различной тональности. Вокруг бокала появлялась радиальная рябь. Галилей отметил, что при изменении высоты тона на октаву рябь усиливается. Чтобы сделать количественную оценку, он сопоставил массу единице длины и подсчитал, что частота тона зависит от корня квадратного из «размера» струны. Впоследствии Галилей дал правило для определения частот колебаний струн, сделанных из разных материалов.
ника, определяемой его длиной. Он соорудил простую систему — погрузил бокал почти по самый край в сосуд с водой и, слегка ударяя по краю, извлекал из бокала звуки различной тональности. Вокруг бокала появлялась радиальная рябь. Галилей отметил, что при изменении высоты тона на октаву рябь усиливается. Чтобы сделать количественную оценку, он сопоставил массу единице длины и подсчитал, что частота тона зависит от корня квадратного из «размера» струны. Впоследствии Галилей дал правило для определения частот колебаний струн, сделанных из разных материалов.