Методика преподавания математики Учебное пособие Специальность 050201 «Математика» Канск 2011
| Вид материала | Учебное пособие |
- Программа учебной дисциплины история математики специальность 050201 математика с дополнительной, 409.11kb.
- Базовая учебная программа дисциплины «методика преподавания математики» для студентов, 108.53kb.
- Курс: 3 Семестр: 6 Перечень вопросов к зачету: Частная методика ( математика, алгебра,, 29.41kb.
- Методика преподавания математики рабочая программа Программа лекционного курса Планы, 266.77kb.
- Методика преподавания математики рабочая программа Программа лекционного курса Планы, 384.99kb.
- Методика формирования исследовательской компетентности школьников в области приложений, 378.99kb.
- Рабочая программа по дисциплине «фтд 02 Изучение школьных учебников математики с углубленным, 119.15kb.
- Контрольная работа по дисциплине «Методика преподавания математики», 60.4kb.
- Задачи как средство развития креативности мышления у младших школьников специальность, 351.93kb.
- Краткий курс лекций учебной дисциплины «Методика преподавания начального курса математики», 631.78kb.
Министерство образования и науки Красноярского края
КГАОУ СПО «Канский педагогический колледж»
Методика преподавания математики
Учебное пособие
Специальность 050201 – «Математика»
Канск 2011
Печатается по решению Педагогического совета колледжа
Автор-составитель: Л.Н. Брагина, преподаватель Канского педагогического колледжа.
Рецензент: Е.В. Чепикова, учитель математики высшей квалификационной категории МБОУ Гимназия № 1 г. Канска, руководитель городского методического объединения учителей математики г. Канска
Методика преподавания математики: учебное пособие / автор-сост. Л.Н. Брагина, рец. Е.В. Чепикова; КГАОУ СПО «Канский педагогический колледж». Канск, 2011. – 39 с.
Пособие содержит зачетные задания по методике преподавания математики. Пособие может быть использовано с целью организации самостоятельной работы студентов при подготовке к практическим занятиям и текущему и итоговому контролю, организации практических занятий, подготовке к Итоговой Государственной аттестации.
Настоящее пособие предназначено для студентов специальности 050201 «Математика» по дисциплине «Методика преподавания математики».
© КГАОУ СПО «Канский
педагогический колледж»
Логико-математический анализ определений понятий и
объектов. Основные этапы их формирования
Основные вопросы.
- Понятие: содержание, объем понятий и связь между ними.
- Определение понятий. Логико-математический анализ определений понятий и их объектов.
- Этапы формирования понятий.
Умения.
- На основе систематизации теоретических знаний о видах и структуре определений понятий и объектов и анализа школьных учебников математики раскрывать логико-математическую структуру типичных для школьного курса математики понятий и объектов.
- Формулировать основные учебные задачи, которые необходимо решать при формировании математических понятий и объектов и адекватные или учебные действия.
- Раскрывать на конкретных примерах основные этапы изучения математических понятий в школе. Раскрывать математическую трактовку некоторых фундаментальных понятий курса математики, подбирать из литературы или школьных учебников другие трактовки одних и тех же понятий.
- Подбирать возможные средства, с помощью которых раскрывалась бы структура определения.
Литература
- Методика преподавания математики в средней школе. Общая методика. Учебное пособие для физико-математического факультета пединститутов. (Ю.М. Колягин., В.А. Оганесян и др.) М., Просвещение. 1980.
- Болтянский В.Г. Использование логической символики при работе с определениями. (Математика в школе.1973 N 5 стр. 45-50)
- Валейкин Н.Я., Абайдулин С.К., Таварткиладзе Р.К. . Определения в школьном курсе математики и методика работы над ними. (Математика в шк. 1984. N 4/ c.43-47)
- Современные проблемы методики преподавания математики: сб. статей. Учебное пособие для математики и физ-мат. спец. пединститутов. (сост. Н.С. Антонов, В.А. Гусев), М., Просвещение. 1985).
- Груденов Л.И. Изучение определений, аксиом, теории. Пособие для учителей. М., Просвещение 1981.
- Груденов Л.И. Совершенствование методики работы учителя математики. Книга для учителя. М., Просвещение. 1980.
- Епишева О.Б., Крупич В.И. Учить школьников учиться математике. М., Просвещение, 1990.
Зачетные задания:
| Практические задания | Умения |
| |
| Выделение объема и содержания понятий, установление связи между ними. |
а) наблюдение, анализ, сравнение, заключение по аналогии, абстрагирование, обобщение, индуктивное умозаключение, конкретизация; б) определение понятий (через ближайший род и видовое отличие), приведение контрпримеров, выведение следствие из определения, подведение под понятие, доказательство равносильности различных определений, систематизация, классификация, специализация. | Выделение объема и содержания понятий, установление связи между ними. |
Проиллюстрируйте круговыми схемами. | Классификация объема понятий. |
а) квадрата б) параллелограмма.
а) две стороны трапеции параллельны; б) оба угла при большем основании острые; в) сумма углов трапеции прилежащих к одной боковой стороне равна 180°; г) основание трапеции горизонтальны; д) оба угла при меньшем основании тупые.
а) вертикальные и смежные углы; б) круг и квадрат; в) линейное и квадратное уравнение; г) линейное уравнение и линейное неравенство; д) линейное уравнение и тригонометрическое уравнение; е) линейное уравнение и прямоугольник; ж) прямоугольный треугольник и функция у = х2 ; з) 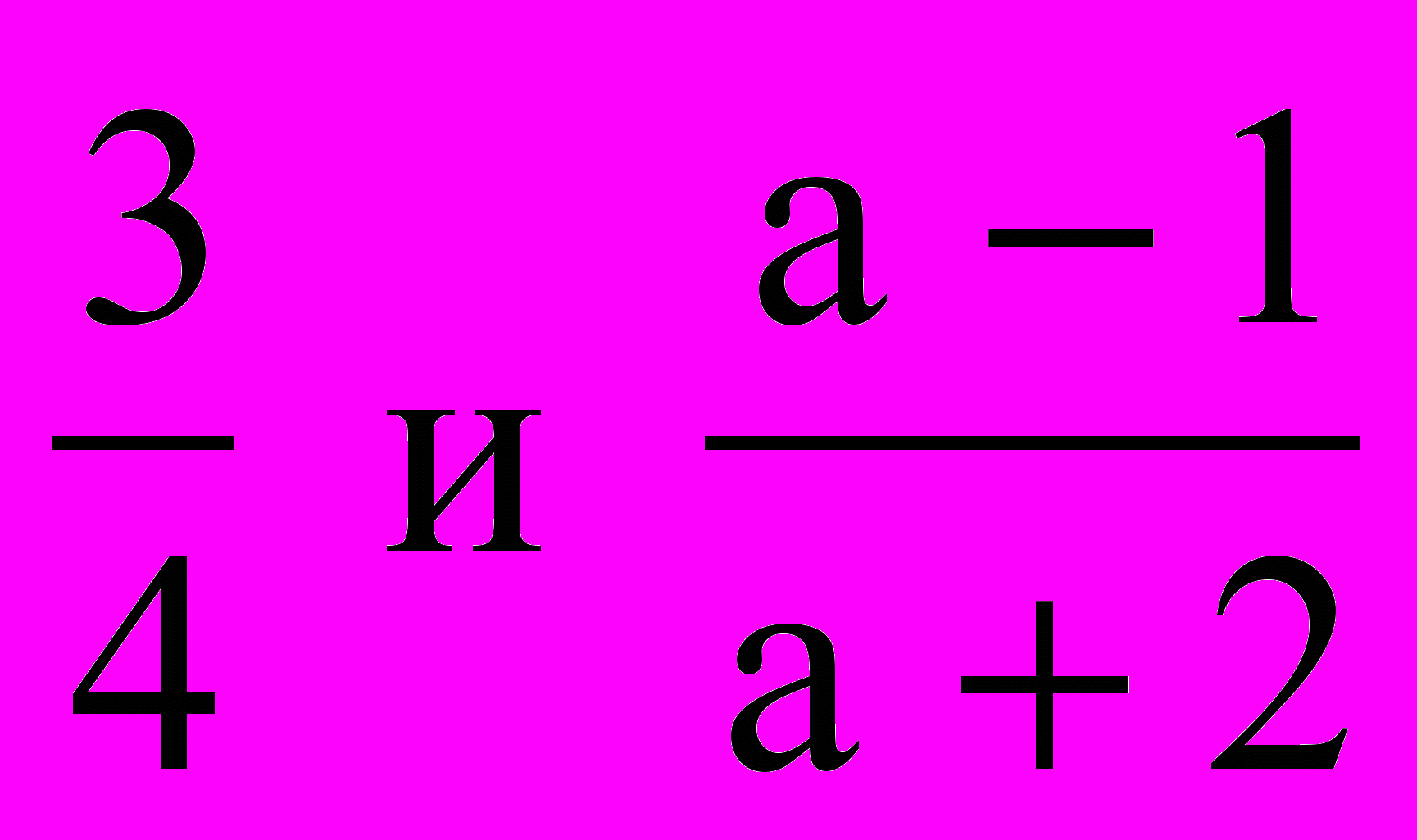 ; ;и) а2 + b2 и х3 + у3 ; к) равенство и уравнение.
а) 1, 4, 9, 16 ... ; б) 82, 97, 114, 133 ... . | Выделение общих и существенных свойств. |
а) угол, смежный с каким- либо углом многоугольника называется внешним углом этого многоугольника; б) прямым углом называется угол равный 90°; в) острым углом называется угол, меньший 90°; г) треугольник называется прямоугольным, если один из его углов прямой; д) пятиугольник - это многоугольник с пятью сторонами; е) две различные прямые, лежащие в одной плоскости и непересекающиеся называются параллельными; ж) отрезок, соединяющий середины двух сторон треугольника, называется его средней линией; з) два одноименных многоугольника называются подобными, если углы одного соответственно равны углам другого, а стороны заключающие равные углы, пропорциональны; и) если точка О является серединой отрезка АВ, то точки А и В называются симметричными точками, относительно точки О; к) числа, которые можно записать в виде обыкновенных дробей, называются рациональными; л) тождеством называется равенство, верное при любых значениях переменной; м) уравнение вида ах = b, где х - неизвестное, а и b - числа, называется линейным уравнением с одним неизвестным; н) значение неизвестного, которое обращает уравнение в верное равенство называется корнем уравнения.
а) квадрат б) вертикальные углы в) хорда г) степень с натуральным показателем д) простое число е) квадратный корень ж) уравнение з) неравенство.
а) Квадрат - это четырехугольник ... . б) Квадрат - это параллелограмм ... . в) Квадрат - это прямоугольник ... . г) Квадрат - это ромб ... .
а) Прямоугольник - это ... , у которого противоположные углы прямые. б) Прямоугольник - это ... , у которого четыре стороны и углы прямые. в) Треугольник - это ... , с наименьшим числом сторон. | Усвоение родовых и видовых признаков и связей между ними. Усвоение родовых и видовых признаков и связей между ними. |
а) ромб б) параллелограмм в) прямой угол г) уравнение.
а) окружности б) перпендикулярных прямых в) конуса г) арифметической прогрессии.
а) формально-логическое; б) конструктивное; в) отрицательное г) неявное определение исходных понятий. | Определение понятий. |
пропорциональное число - это 1) неизвлекаемый корень; 2) бесконечная десятичная дробь. | Логический анализ определений понятий. |
1. а) Две пересекающих плоскости называется перпендикулярными, если третья плоскость перпендикулярная прямой перечисления этих плоскостей пересекает их по перпендикулярным прямым. б) Две плоскости называются взаимно-перпендикулярными, если в каждой из них через любую точку проходит прямая, перпендикулярная другой плоскости. 2. а) Угол в 90° называется прямым. б) прямым углом называют половину развернутого угла. 3. а) Равенство содержащее неизвестное число, обозначенное буквой, называют уравнением. б) Равенство, содержащее неизвестное называется уравнением. | Установление эквивалентности определений |
а) есть центр симметрии; б) противоположные углы попарно равны; в) каждой диагональю четырехугольник делится на равновеликие части.
а) с равными гипотенузами; б) с одной парой равных катетов.
а) 3,4 х2 у г) х2 х ж) а - b к) -0,3 ху2 б) а (--8) д) 0,5m 2 n з) е10 л) 2(х + у) 2. в) х2 + х е) -bca и) 0,6
а) у = 2х - 3 б) у = 7 - 9х в) у = 8х г) у=  д) у = 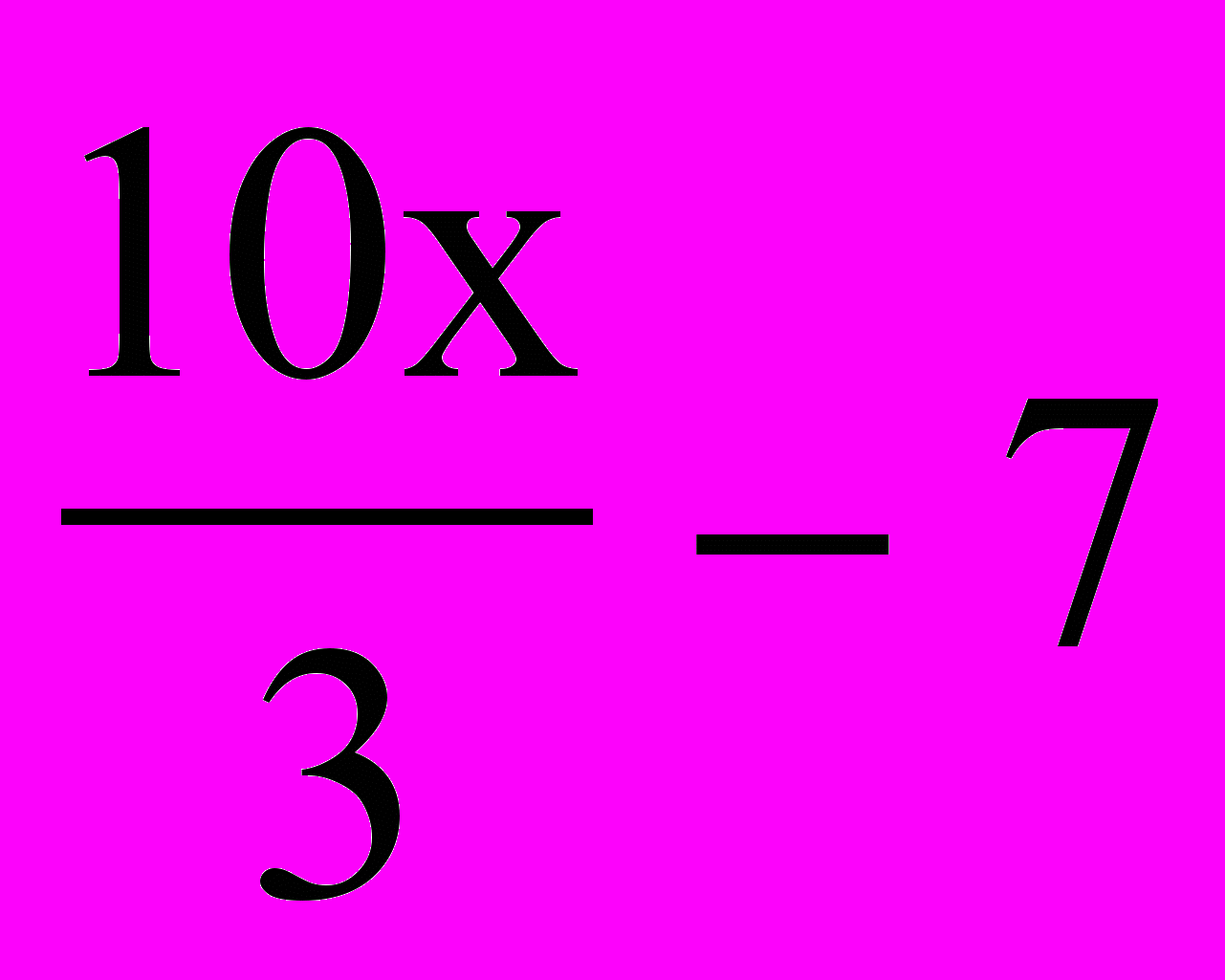 е) у = х2 - 3 е) у = х2 - 3 ж) у = 4(х - 3) + (х + 3).
а) 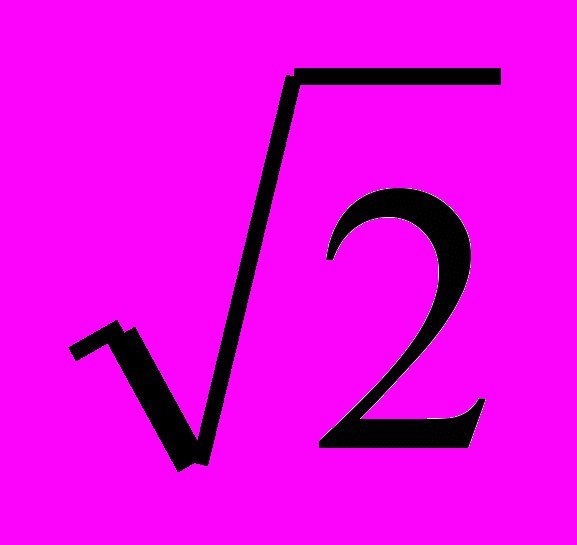 + х = 5 + х = 5б) 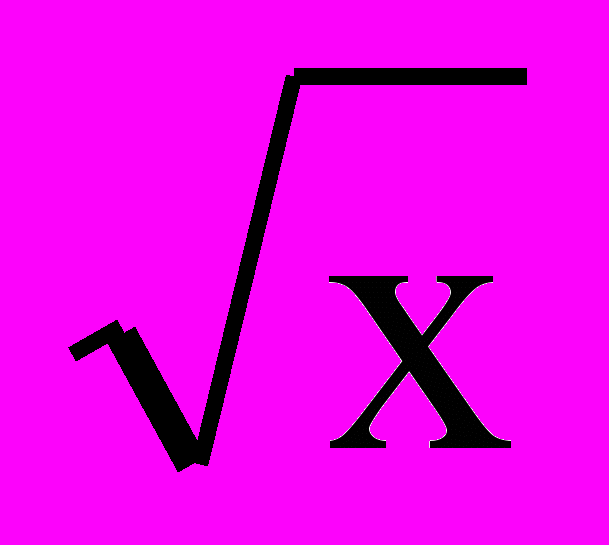 + 2 = 5 + 2 = 5в) 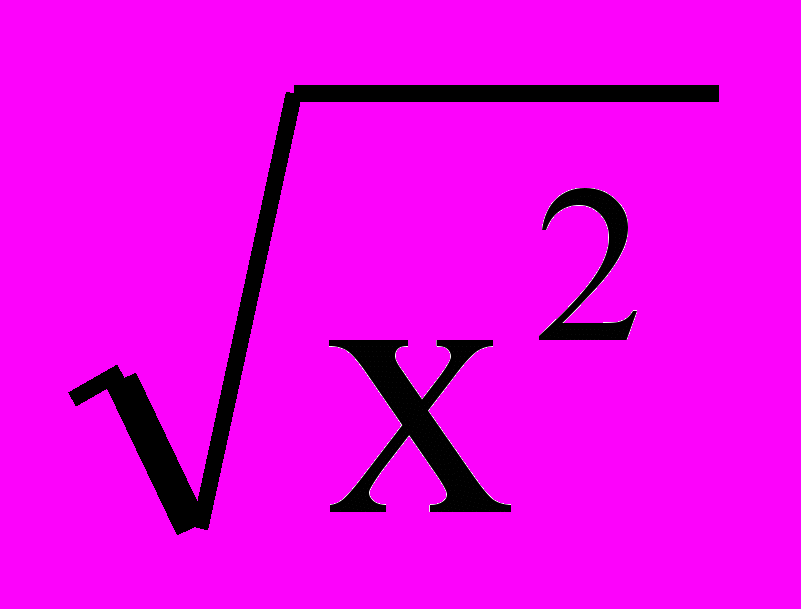 -5 = 0,5х -5 = 0,5х
а) х - 2 = 0 и (х - 2)(х + 2) = 4(х + 2) б) 3х - 2 = х и 3х - 2 + 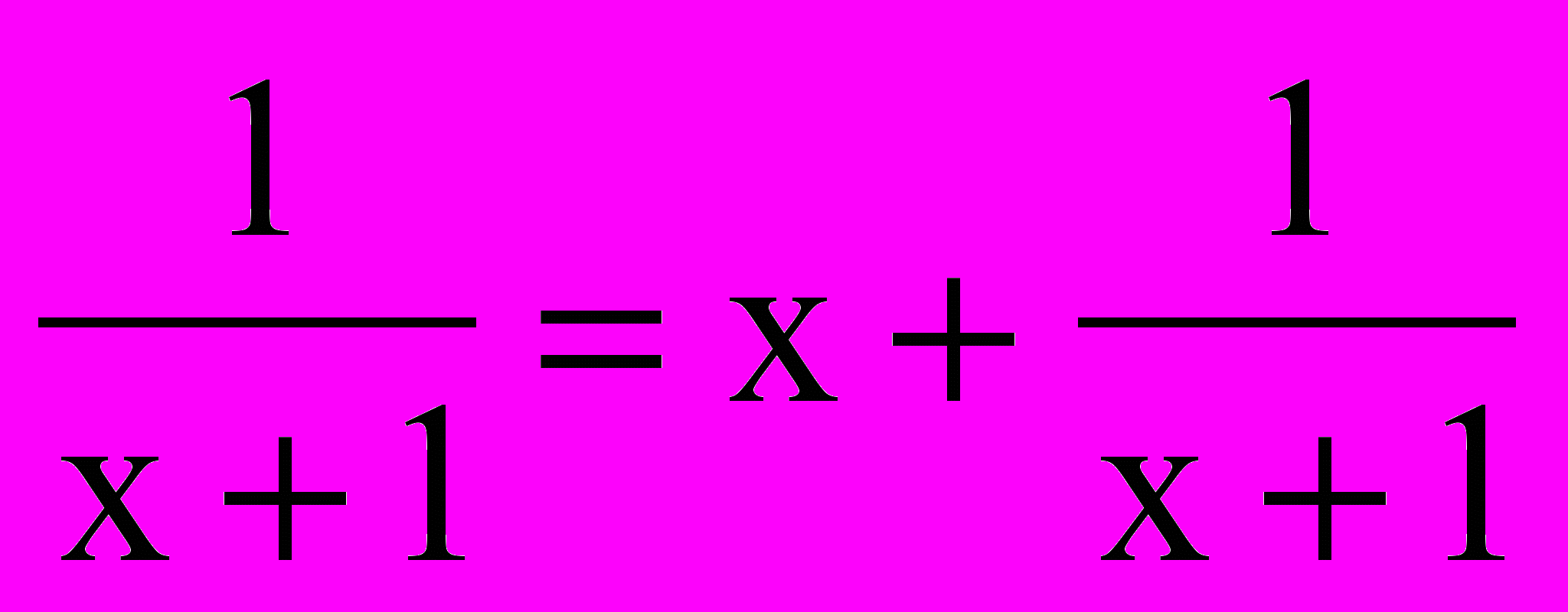 в) х = 3 и х2 = 9.
а) линейная функция; б) симметричные точки; в) скрещивающиеся прямые; г) убывающая функция; д) геометрическая прогрессия. Результаты занесите в таблицу (см. лекцию) | Действие получения следствий из факта принадлежности конкретного объекта теоретическому. Подведение под понятие. |
а) арифметический квадратный корень; б) правильная и неправильная дроби; в) отрезок; г) равнобедренный треугольник. | Выведение следствий из определения. |
а) ромб, параллелограмм, четырехугольник, многоугольник; б) отрезок, прямая; в) параллельные прямые, скрещивающиеся прямые; г) полукруг, круг.
а) равносторонний четырехугольник, ромб; б) трапеция, параллелограмм; в) равнобедренный треугольник, прямоугольный треугольник. 26. Проведите обобщение и специализацию понятий: треугольник, трапеция, многоугольник, выражение, равенство, уравнение, функция, геометрическая фигура, целое число. | Обобщение и специализация. |
Какие знания и умения необходимы для решения этих учебных задач. | Формулирование учебных задач и действий им адекватным. |
а) наблюдение, анализ, сравнение, заключение по аналогии, абстрагирование, обобщение, индуктивное умозаключение, конкретизация; б) определение понятий, приведение контрпримеров выведения следствий из определения; доказательство равносильности, подведение под понятие доказательство равносильности определений, систематизация классификация, специализация. | Составление алгоритмов. |
Является ли система задач полной? Почему некоторые виды задач отсутствуют? Какими задачами целесообразно систему дополнить. | Анализ системы задач на усвоение понятия и его определения. |
| |
| 31. Опишите методику работы с одним из понятий. |
|

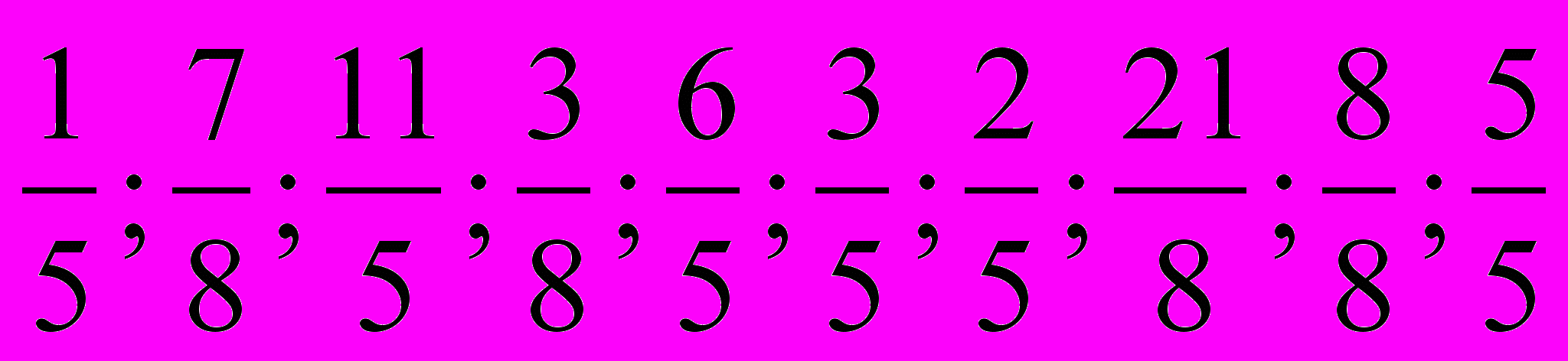 по двум признакам: правильная и неправильная дроби и дробь со знаменателем 5. Проиллюстрируйте классификацию круговыми схемами.
по двум признакам: правильная и неправильная дроби и дробь со знаменателем 5. Проиллюстрируйте классификацию круговыми схемами.