Geum.ru

Методика преподавания математики Учебное пособие Специальность 050201 «Математика» Канск 2011

Вид материалаУчебное пособие

Содержание


Логико-математический анализ математических утверждений.Общие приемы работы с теоремой
Будут ли сформулированные утверждения теоремами. Почему?
Будут ли утверждения теоремой?
Являются ли сформулированные утверждения - теоремами? Почему?
Какие из них одновременно являются теоремами?
Подобный материал:
1   2   3   4

Логико-математический анализ математических утверждений.
Общие приемы работы с теоремой



Основные вопросы.
  1. Понятие утверждения, теоремы.
  2. Логическая структура теоремы.
  3. Виды теорем.
  4. Способы доказательств.
  5. Общие приемы работы с теоремой.


Умения.
  1. Выполнять логико-математический анализ конкретных утверждений.
  2. Самостоятельно анализировать теоремы школьного курса математики.
  3. Владеть основными способами доказательств.
  4. Раскрывать этапы изучения теорем.


Литература:
  1. А. А. Столяр. Педагогика математики. Минск, 1986.
  2. Методика преподавания математики в средней школе. Общая методика.
  3. Я. И. Груденов. Изучение определений, аксиом, теорем. Пособие для учителя. Просвещение, 1981.
  4. Я. И. Груденов. Совершенствование методики работы учителя математики. Просвещение, 1990.
  5. Л. С. Атанасян и др. Геометрия 7-9кл.
  6. А. В. Погорелов. Геометрия 7-11 кл.


Зачетные задания:


Практические задания
Умения
  1. Ответьте на вопросы:
  • Что такое теорема, утверждение?
  • Чем отличается теорема от утверждения?
  • Что такое разъяснительная часть, условие, заключение?
  • В каких формах могут быть сформулированы утверждения?
  • Как выделить условие и заключение утверждений?


  1. Выполните логико-математический анализ утверждений, ответив на вопросы:
  • В какой форме сформулировано утверждение?
  • Сформулируйте утверждение в импликативной форме.
  • Выделите разъяснительную часть.
  • Выделите условие и заключение утверждений.
  • Установите, в зависимости от числа условий и заключений, является ли данное утверждение простым или сложным.

а) сумма углов треугольника равна 180°;

б) если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны;

в) в равнобедренном треугольнике биссектриса, проведенная к основанию является медианой и высотой.
Логический и математический анализ утверждений.
  1. Прочитайте различными способами утверждения, сформулированные в п.2
Чтение утверждений.

4. Для утверждений из п.2, сформулируйте утверждения, обратные данным.

Будут ли сформулированные утверждения теоремами. Почему?
Формулирование утверждения обратного данному.
  1. Для утверждений из п.2, сформулируйте утверждения, противоположные данным.

Будут ли утверждения теоремой?
Формулирование утверждения противоположного данному.

6. Сформулируйте утверждения противоположные обратным (обратные противоположным).

Являются ли сформулированные утверждения - теоремами? Почему?
Формулирование утверждения обратного противоположному.

7. На основании рассмотренных примеров сделайте вывод о взаимосвязи между прямым, обратным, противоположным и обратным противоположному утверждениям.

Какие из них одновременно являются теоремами?



8. Исправьте ошибки в следующих утверждениях:

а) в треугольниках, против равных углов лежат равные стороны;

б) в треугольнике АВС сторона АВ=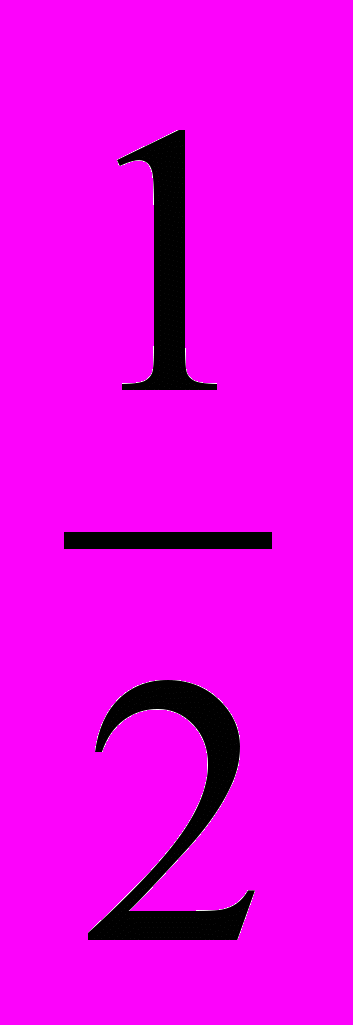ВС, т.к. она лежит против угла в 30°;

в) биссектриса угла треугольника является его медианой и высотой.
Формулирование утверждений.

9. Верны ли следующие предложения?

А) Чтобы треугольник был прямоугольным, достаточно, чтобы сумма двух углов равнялась 90°.

Б) Чтобы четырехугольник был параллелограммом, достаточно, чтобы его диагонали делились в точке пересечения пополам.

В) Для того, чтобы число делилось на 2, необходимо. Чтобы оно оканчивалось нулем.

Г) для того, чтобы число делилось на 10 необходимо и достаточно, чтобы оно делилось на 2 и 5.
Определение необходимых и достаточных условий.

10. Какие слова “необходимо”, “достаточно” или “необходимо и достаточно” можно поставить вместо многоточия в следующих предложениях, чтобы получить верные высказывания?

а) Чтобы произведение двух чисел равнялось нулю , чтобы каждое из них равнялось нулю.

б) Чтобы четырехугольник был параллелограммом …, чтобы две стороны его были параллельны.

в) Чтобы сумма двух целых чисел была четным числом …, чтобы каждое из слагаемых было четным числом.

г) Чтобы плоскость содержала прямую …, чтобы они имели две общие точки.
Определение необходимых и достаточных условий.

11. Сформулируйте со словом “необходимо” следующие высказывания:

а) вертикальные углы равны;

б) две прямые пересекаются только тогда, когда они лежат в одной плоскости.
Определение необходимых и достаточных условий.

12. Сформулируйте следующие высказывания со словом “достаточно”:

а) четырехугольник является ромбом тогда, когда все его стороны равны;

б) фигуры равновелики тогда, когда они равны;

в) график функции у = f(х) симметричен относительно оси ОY тогда, когда функция у = f(х) четная.
Определение необходимых и достаточных условий.

13. Объясните, в каком случае условие теоремы является и необходимым и достаточным для заключения этой теоремы.
Определение необходимых и достаточных условий.

14. а) сформулируйте известные вам теоремы о параллельных прямых, выделив условие и заключение;

б) сформулируйте теоремы им обратные;

в) какие из них теоремы – свойства, какие признака;

г) как отличить теорему – свойство от признака;

д) можно ли теоремы разбить на 2 группы:

I – теоремы свойства;

II– теоремы признаки.

Разбейте теоремы из учебника (5) или (6) на группы.
Формулирование свойств и признаков объектов.

15. Раскройте операционный состав
  • анализа текста утверждения;
  • приема развертывания условия;
  • приема последовательного анализа условия и заключения.
Общие приемы поиска и проведения доказательств.

16. Используя прием развертывания условия, осуществите доказательство утверждения.

а) Если прямая, не проходящая ни через одну из вершин треугольника пересекает одну из сторон треугольника, то она пересекает только одну из двух других сторон треугольника.

б) В четырехугольнике два противолежащих угла тупые. Доказать, что диагональ, соединяющая их вершины, короче другой.

в) Докажите, что общая хорда двух пересекающихся окружностей перпендикулярна линии центров.
Прием развертывания условия.

17. Раскройте в виде схемы прием развертывания условия и заключения на примере следующих задач.

а) В треугольнике проведены две биссектрисы. Докажите, что если их отрезки от точки пересечения до вершин равны, то этот треугольник равнобедренный.

Б) Докажите, что в прямоугольном треугольнике, медиана, проведенная к гипотенузе, равна ее половине.

В) Окружность, построенная на стороне АС треугольника АВС как на диаметре, пересекает стороны АВ и СВ соответственно в точках К и D. Докажите, что CD и АК высоты треугольника АВС.
Прием последовательного разверты-вания условия и заключения.

18. Докажите разными методами:

а) теорему о средней линии треугольника;

б) в равнобедренном треугольнике медианы, проведенные к боковым сторонам равны.
Умение доказывать разными методами.

19. Приведите несколько доказательств теоремы о сумме внутренних углов треугольника дедуктивным методом, используя в каждом случае различные основания для доказательства.
Умение использовать различные основания при доказательстве утверждения одним методом

20. Докажите утверждения методом от противного:

а) если две различные прямые пересекаются, то их пересечение содержит одну и только одну точку;

б) в разностороннем треугольнике биссектриса угла не перпендикулярна противолежащей стороне;

в) ни один треугольник не может иметь два прямых угла.
Умения доказывать методом от противного.

21. Докажите утверждение методом контрапозиции.

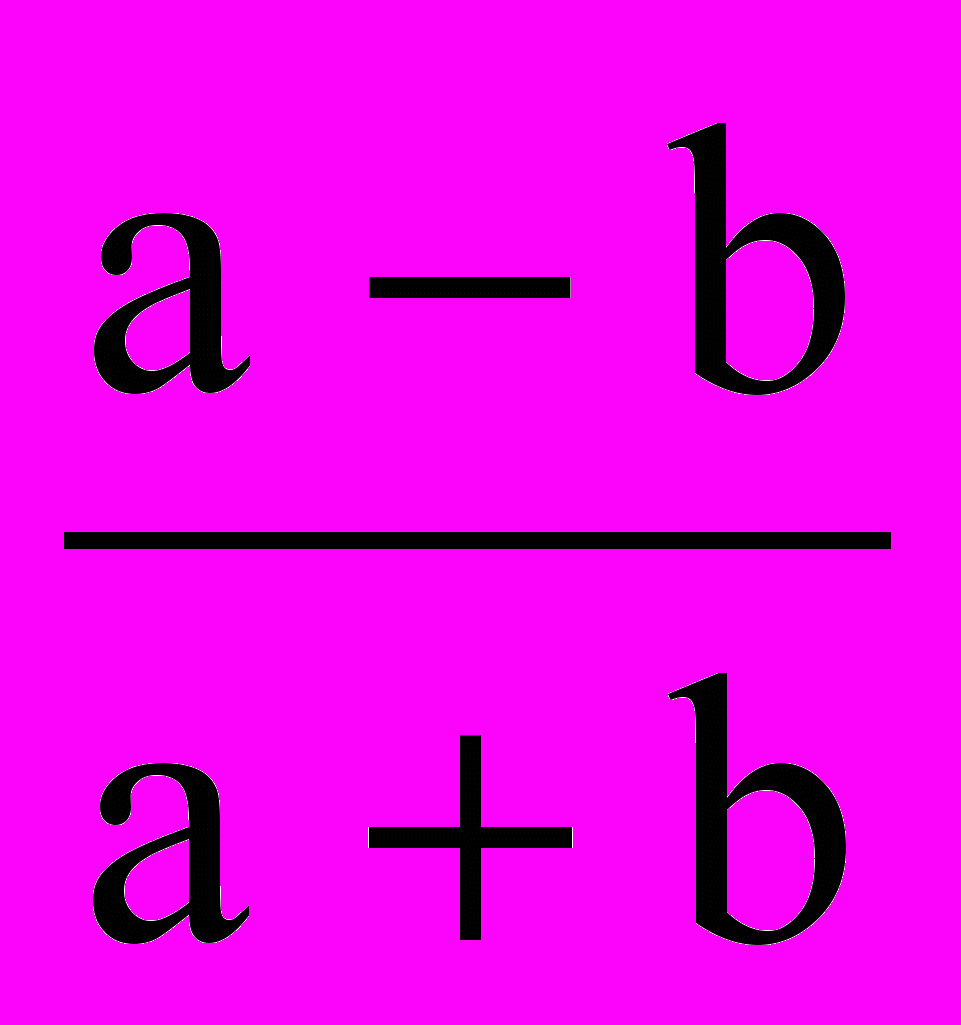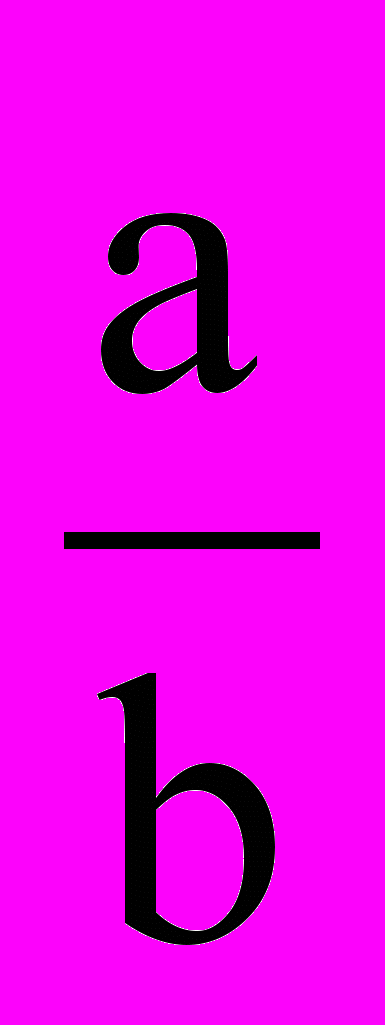а) Доказать, что если дробь несократима, то и дробь несократима.
Умение доказывать методом контрапозиции.

Для того, чтобы

доказать
Достаточно

доказать

1) равенство треугольников
1.

2.

………………………..

2) треугольник равнобедренный
1.

2.

………………………..

3) прямые параллельны
1.

2.

………………………..




22. Разработайте различные формы записи доказательств математических утверждений.
Умение оформлять доказательство.

23. Для формирования каких умений можно предлагать учащимся следующие задания.

а) Выделите, о чем говорится в следующих предложениях, и что говорится о выделенном объекте:
  • если знаменатель выражения не равен нулю, то данное выражение имеет смысл;
  • сумма смежных углов равна 180;
  • вертикальные углы равны.

б) Составьте список свойств следующих объектов: луч, отрезок, треугольник, параллелограмм.

в) Известно, что точки А и К лежат в различных полуплоскостях относительно данной прямой. Какие выводы можно сделать, из того условия.

г) По данным чертежам сформулируйте утверждения, которые можно доказать: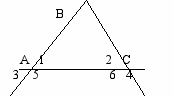




Дано: АВ = ВС

Доказать: ?
Умение определять дидактическую цель задания.



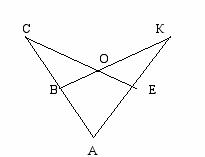Дано: АС = АК

ВС = ЕК

Доказать: ?

д) Даны две полупрямые. Что должно быть известно, чтобы можно было утверждать, что дан угол? Что дан развернутый угол?

е) Что достаточно знать, для того, чтобы утверждать, что данный треугольник – равнобедренный.

ж) Известно, что выполняются равенства АВ = МР и ВС = РК. Дополните это условие так, чтобы можно было сделать вывод, что АВС = МРК.

з) Составьте карточку вида




24. Сформулируйте учебные задачи, решаемые в процессе изучения математических утверждений и способов их доказательств. Какие знания и умения необходимы для решения этих учебных задач.
Умение формулировать учебные задачи.

25. Активизируйте общие приемы работы с теоремой.



26. Проанализируйте задачи № 12–24 (6) с точки зрения удовлетворения требованиям, предъявляемым к системе задач для усвоения теорем и их доказательств.
Анализ системы задач на усвоение теоремы и ее доказательства.

27. Опишите методику работы с одной из теорем.
  1. Умение определять цели изучения конкретного материала.
  2. Умение мотивировать.
  3. Умение ставить учебную задачу.
  4. Умение анализировать урок с учетом цели.
  5. Логико-математический анализ теоремы.
  6. Умение вести поиск доказательства.
  7. Умение оформлять доказательство.
  8. Умение подбирать задачи для усвоения теоремы.
  9. Умение подбирать средства обучения.

28. Выполните математический анализ правил (алгоритмов):
  • метод интервалов;
  • сложение дробей с разными знаменателями;
  • умножение одночлена на многочлен.
Математический анализ правила (алгоритма).

29. Запишите эти алгоритмы в различном виде.
Умение представлять алгоритм в различной форме.

30. Актуализируйте общие приемы работы с правилом (алгоритмом).



31. На основании логико-математического анализа алгоритма из п. 29а. Составьте системы задач для каждого этапа формирования алгоритма.
Анализ системы задач на усвоение правила.

32. Опишите методику работы с одним из правил.
1.Умение определять цели изучения конкретного материала.

2.Умение мотивировать.

3.Умение ставить учебную задачу.

4.Умение выполнять математический анализ правила.

5.Умение подбирать задачи для усвоения правила.

6.Умение подбирать средства обучения.

.