Рабочая программа по дисциплине «фтд 02 Изучение школьных учебников математики с углубленным содержанием». специальность

Вид материала

Рабочая программа

Содержание Организационно-методический раздел. 1.2. Требования к уровню освоения содержания дисциплины. 2.2 Темы, их содержание и объём в часах лекционных занятий. 3.2 Практические занятия. Их содержание и объём в часах. 4.2 Вопросы для самостоятельного изучения. 4.4 Основная литература.

Подобный материал:

• Рабочая программа по факультативной дисциплине: «фтд 02. 3 Моделирование уроков в классах, 105.29kb.
• Рабочая программа по дисциплине Введение в специальность Аббревиатура специальности, 184.92kb.
• Рабочая программа по дисциплине дс. 03. Математическое моделирование физических процессов, 112.58kb.
• Программа дисциплины фтд. 00 «практикум по решению математических задач» Специальность, 275.82kb.
• Контрольная работа пометодикепреподавани я математик идля студентов-заочников 4 курса, 156.75kb.
• Программа дисциплины дпп. Дс. 02 «элементы геометрии в классах с углубленным изучением, 163.1kb.
• «Изучение вероятностно-статистического материала в обязательном основном школьном курсе, 459.12kb.
• Рабочая программа по дисциплине: «Моделирование случайных процессов с помощью математического, 72.45kb.
• Рабочая учебная программа по дисциплине «Аудирование английского языка» для специальности, 126.86kb.
• Рабочая программа по дисциплине: «Химия» Специальности, 143.11kb.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Елецкий государственный университет им. И.А. Бунина

“Утверждаю”

Зав. кафедрой ______/О.А. Саввина./

“___”_____________200_ г.

РАБОЧАЯ ПРОГРАММА

по дисциплине	«ФТД 02.4. Изучение школьных учебников математики с углубленным содержанием».
специальность	050201 – Математика с доп. спец. «Информатика»
квалификация	учитель математики и информатики учитель математики и физики
форма обучения	заочная
срок обучения	6 лет
факультет	физико-математический
кафедра	математического анализа и элементарной математики
курс:	5, 6
семестр:	10, 11
лекций:	-
практических занятий:	28 часов
зачет:	10, 11 семестр
самостоятельная работа:	28 часов
Всего часов:	56 часов

Елец – 2007

Рабочая программа разработана на основе ГОС по специальности 050201 – Математика с дополнительной специальностью на кафедре математического анализа и элементарной математики.


Рабочая программа рассмотрена на заседании кафедры (протокол №_____, от “___”______________200 г.)


Зав. кафедрой________________________(О.А. Саввина)


Рабочая программа утверждена методическим советом университета (факультета) (протокол №______ от “__”__________ 200__г.)


Председатель методического совета ___________ / ./


Рабочую программу составили Е.А. Добрина, Т.Е. Рыманова

1. Организационно-методический раздел.
   

1. . Пояснительная записка.
   

Дисциплина “Изучение школьных учебников математики с углубленным содержанием” входит в комплекс взаимосвязанных курсов методического цикла и является логическим продолжением “теории и методики обучения математики” и предшествующих факультативных курсов. В связи с этим в программу включены общие проблемы теории и методики обучения математики и ключевые вопросы методической подготовки будущих учителей.

С учётом знаний необходимых учителю раскрываются особенности обучения учащихся в классах с углубленным изучением математики. Изучение курса имеет целью дать будущим педагогам необходимый объём теоретических умений и навыков, которые позволят молодому специалисту преподавать математику в условиях профильной дифференциации.

Основными задачами являются: 1) подготовка студентов к самостоятельной творческой деятельности по учебникам математики с углубленным содержанием, 2) формирование у будущих учителей продуктивного методического мышления для реализации на практике идей развивающего обучения школьников с учётом индивидуализации. Для ускоренного усвоения курса студентам необходимо усвоить разделы алгебры, теории чисел, геометрии, математического анализа, теории вероятности.

1.2. Требования к уровню освоения содержания дисциплины.

В результате изучения курса:

а) студенты должны знать.

- методические особенности использования множественного подхода.

- методические подходы к введению понятия действительного числа.

- методические аспекты изучения многочленов.

- особенности изучения элементов теории пределов в средней школе.

- методические возможности изучения функциональной линии.

Линии уравнений и неравенств.

- методические аспекты изучения вопросов математического анализа

в математических классах.

- методику изучения элементов комбинаторики и теории вероятности.

- основные методические направления изучения геометрии в математических классах.

- связи геометрии с другими дисциплинами естественно – научного цикла.

б) студенты должны знать:

- выполнять операции над множествами.

- выполнять действия с действительными числами.

- применять метод мат. индукции при решении задач.

- решать уравнения и неравенства разных типов.

- применять производную и интеграл в решении задач геометрии и физики.

- решать задачи по комбинаторике и теории вероятности.

- решать геометрические задачи повышенной сложности.

- применять векторный метод при решении задач.

- решать задачи на комбинации тел.

2. Содержание дисциплины.
   
   1. Основные разделы дисциплины.
      

1. Множества и числа.
   
2. Функции.
   
3. Уравнения и неравенства.
   
4. Дифференцированное и интегрированное исчисление.
   
5. Векторы.
   
6. Многогранники и тела вращения.
   
7. Площади и объёмы.
   
8. Движения.
   

2.2 Темы, их содержание и объём в часах лекционных занятий.

Лекции программой не предусмотрены.


III. Рабочая программа дисциплины.

3.1. Распределение часов по темам и видам работ.

№	Наименование тем и разделов	Всего часов	Аудиторные занятия		Самостоя тельная работа
			лк	пр
1	Множества и числа	6		6
	Тема 1. Расширение понятия числа	4		4
	Тема 2. Методические особенности использования множественного подхода	2		2
2	Уравнения и неравенства	6		6
	Тема 2. методические особенности изучения линии уравнений и неравенств	6		6
3	Элементы математического анализа	2		2
	Тема 1. Методика изучения элементов теории пределов	2		2
	Контрольная работа	2
4	Первые разделы стереометрии	4		4
	Тема 1. Особенности изучения первых разделов стереометрии	4		4
5	Векторы	4		4
	Тема 1. Методические особенности изучения векторного метода	4		4
6	Пространственные тала	2		2
	Тема 1. Методика изучения темы: “Пространственные тала”	2		2
	Контрольная работа	2

Таблица 1


3.2 Практические занятия. Их содержание и объём в часах.

10 семестр.	14 часов
1. Расширение понятия числа в углубленном курсе математики Методические подходы к введению понятия действительного числа. Рациональные и иррациональные числа. Построение алгоритма обращения периодических десятичных дробей в обыкновенные. Различные подходы к определению комплексного числа и их реализация в углубленном курсе математики. Операции над комплексными числами	2ч
2. Методические особенности использования множественного подхода в школьном курсе математики Обобщение сведений о множестве натуральных чисел. Операции над множествами. Формирование у школьников понятия “полна индукция и неполная индукция”. Цели изучения и суть метода математической индукции. Доказательство тождеств и неравенств методом математической индукции	2 ч
3. Методические особенности изучения уравнений и неравенств в классах с углубленным содержанием. Методы решения логарифмических, показательных и иррациональных уравнений и неравенств. Возможности введения задач с параметрами в средней школе. Рациональные, иррациональные и трансцендентные уравнения и неравенства с параметрами	6ч.
4. Методика изучения элементов теории пределов Методические подходы к введению понятия “предел” и изучению теории пределов. Предел функции на бесконечности. Предел функции в точке. Методика изучения основных теорем	4 ч
11 семестр	10 часов
1. Особенности изучения первых разделов стереометрии в классах с углубленным изучением математики Общая характеристика системы аксиом. Методика изучения аксиом и первых теорем. Обучение школьников конструктивным и неконструктивным доказательствам существования. Логико – дидактический анализ темы: “параллельное проектирование”
2. Методические особенности изучения векторного метода. Различные подходы к введению понятия “вектор”. Обобщение и систематизация знаний по теме: “Векторы и координаты” в курсе стереометрии. Применение векторного метода к решению задач. Методика изучения других систем координат	4 ч
3. Методика изучения темы: “Пространственные тела” Роль наглядности в изложении материала. Основные цели изучения темы. Формирование основных понятий: граница и внутренность фигур в пространстве, тело, граничные и внутренние точки плоских фигур, замкнутая плоскость. Различные подходы к определению “многогранник”, “призма”, “пирамида”. Логико – дидактические анализы тем: “Многогранники”, “Тела вращения”.	6ч

IV. Учебно – методическое обеспечение дисциплины.

1. Типовые контрольные работы.
   

10 семестр.

1. Докажите, для всех натуральных n выполнено равенство:
   

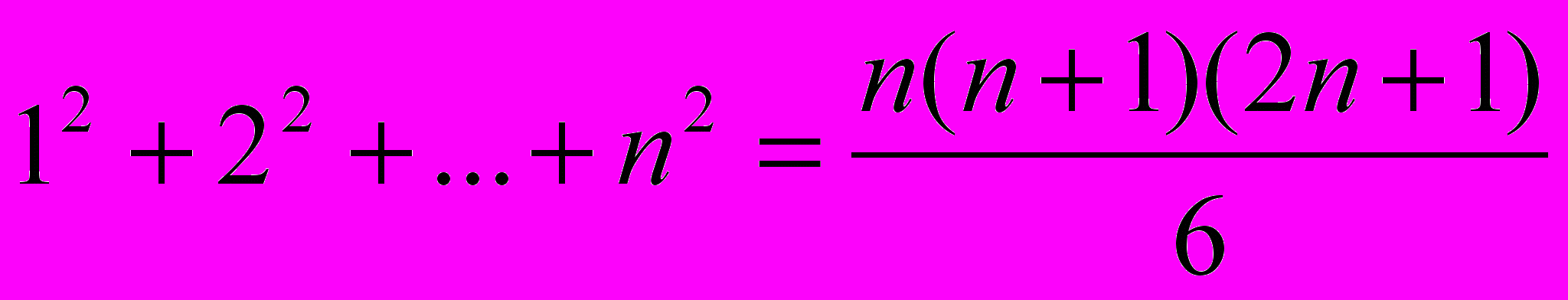
2. Решите уравнения:
   

a)

б)

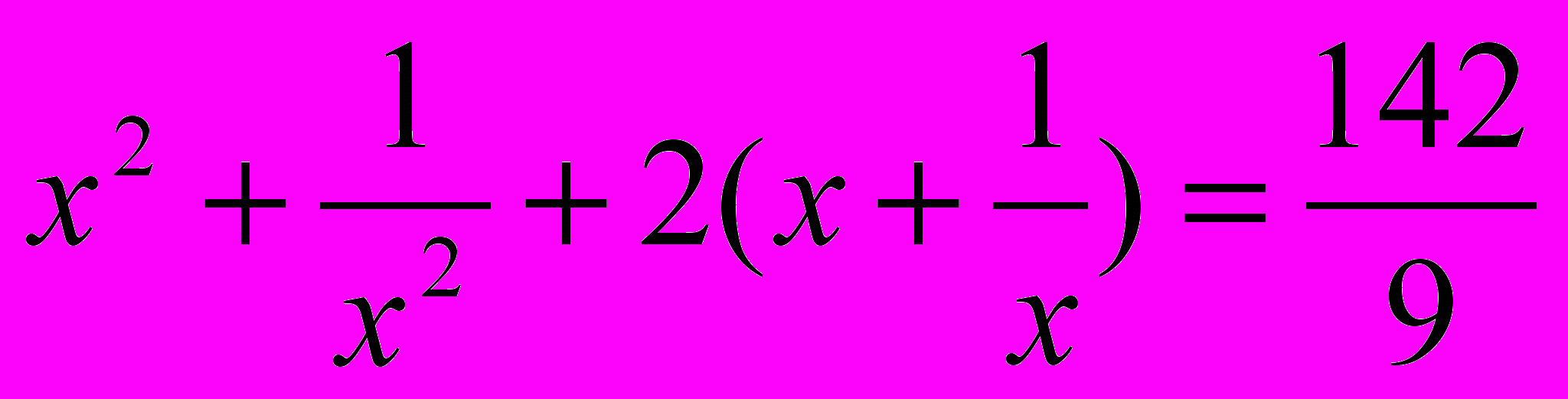
в)

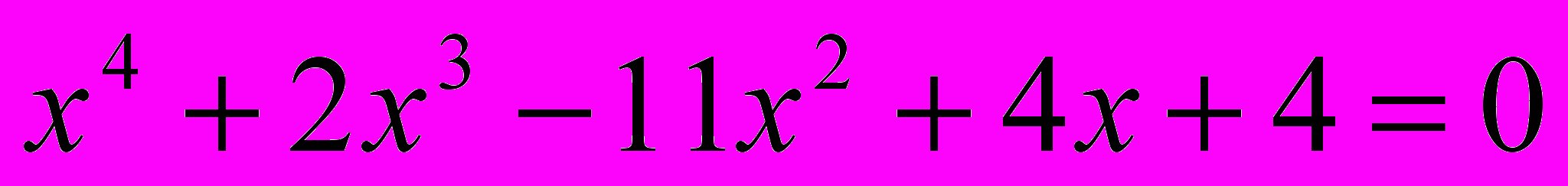
3. Решите неравенство:
   

11 семестр.

Дана треугольная пирамида РАБС, в основании которой лежит равнобедренный треугольник АБС, причём

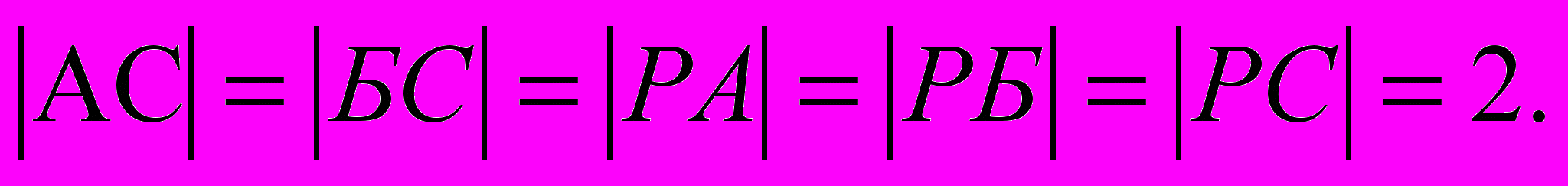
1. Доказать, что (РАБ)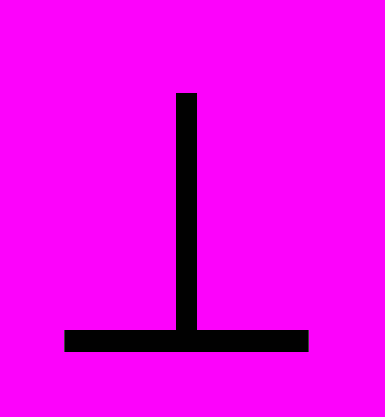(АБС)
   
2. Найти
   
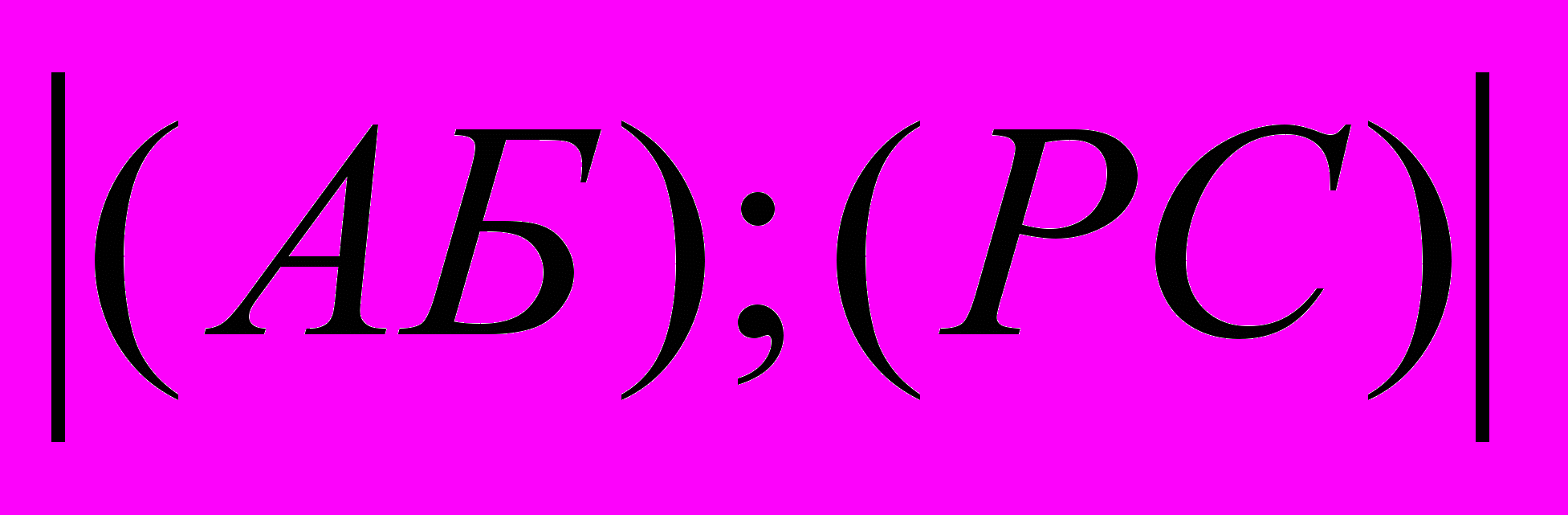
3. Доказать, что 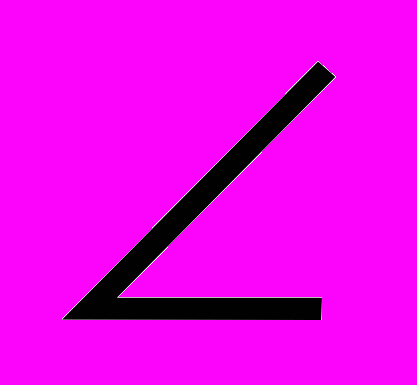((РАС);(АБС)) = 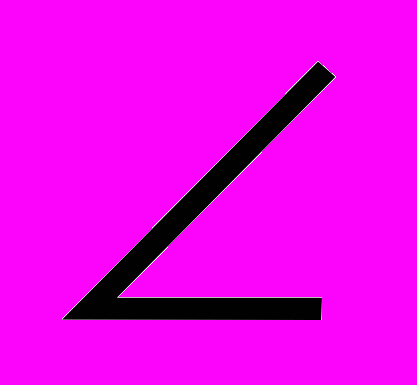((РБС);(АБС)) и вычислить его.
   

4.2 Вопросы для самостоятельного изучения.

1. Уравнения с несколькими переменными.

2. Неравенства с несколькими переменными.

3. Системы уравнений.

4. Системы неравенств.

5. Текстовые задачи на составление неравенств.

6. Различные системы координат.

7. Неевклидовы геометрии.

8. Геометрия и теория относительности.


4.3 Примерный перечень вопросов к зачёту.

10 семестр.

1. Арифметические операции над действительными и комплексными числами.
   
2. Доказательство тождеств и неравенств методом математической индукции.
   
3. Использование свойств степенной, показательной, логарифмической и тригонометрической функции при решении задач, уравнений и неравенств.
   
4. Решение уравнений с абсолютной величиной.
   
5. Использование Бинома Ньютона для приближённых вычислений.
   
6. Решение неравенств с одной переменной.
   
7. Уравнения и неравенства с параметрами.
   
8. Нахождение пределов.
   
9. Нахождение производной функции.
   
10. Решение задач с использованием производной.
    
11. Решение задач с использованием интеграла.
    

11 семестр.

1. Задачи на доказательство с применением аксиом первых теорем стереометрии.
   
2. Построение сечений многогранников.
   
3. Задачи на применение векторного метода.
   
4. Задачи на применение координатного метода.
   
5. Многогранники.
   
6. Тела вращения.
   
7. Вычисление площадей поверхностей.
   
8. Нахождение объёмов пространственных тел.
   
9. Движение в пространстве.
   

Вопросы из перечня, не указанные в таблице 1, студенты изучают самостоятельно.


4.4 Основная литература.

1. Геометрия: Учеб. для 7-9 кл. общеобразоват. учреждений / А.Д. Александров, А.Л. Вернер, В.И. Рыжик. –М.: Просвещение, 1995.
   
2. Геометрия для 10-11 классов: Учеб. пособие для уч-ся шк. И Кл. с углубленным изучением математики. А.Д. Александров, А.Л. Вернер, В.И. Рыжков – М.: Просвещение, 1995 -464с.
   
3. Виленкин Н.Я. и др. Алгебра и математический анализ для 10 класса: Учеб. пособие для учащихся шк. и кл. с углубленным изучением математики. / Н.Я. Виленкин, О.С. Иванов – Мусатов, С.И. Шварцбурд. – 5-е изд.. – М.: Просвещение, 1997. -335с.
   
4. Виленкин Н.Я. и др. Алгебра и математический анализ для 11 класса:-6-е издание. М.: Просвещение, 1998 -288с.
   
5. Галицкий М.Л. и др. Углубленное изучение алгебры и математического анализа: метод. рекомендации и дидакт. материалы: Пособие для учителя / М.Л.Галицкий, М.М. Мошкович. С.И. Шварцбурд -3-е изд., дороб.- М.: Просвещение. 1997.-352с.
   

Дополнительная литература.

1. Башмаков М.И. Алгебра и начало анализа: Учеб. для 10-11 кл.средн. -3-е изд. .-М.: Просвещение,1993-351с.
   
2. Бевз г. П. и др, Геометрия: учеб. для 7-11 кл. общеобразов. учрежд. / Г.П. Бевз, В.Г. Бевз, Н.Г. Владимирова. -2-е изд. – М.: Просвещение,1994.-351с.
   
3. Мордкович А.Г. Алгебра и начало анализа 10-11.: учеб. для общ. Образ. Учрежд. М.: Мисморина,2000-336с.
   
4. Шарыгин И.Ф. Геометрия 10-11 кл. учеб. для общеобразов. чеб. заведений. –М.: Дрофа,1999.-208с.