Академия наук СССР галилео галилей избранные труды в двух томах
| Вид материала | Документы |
- Галилео галилей (Galilei), 238.2kb.
- Галилей галилео галилей галилео, 23.36kb.
- Жизнь и деятельность Галилео Галилея, 159.16kb.
- Галилео Галилей (1564-1642), 46.37kb.
- Отечества избранные психологические труды в 70-ти томах, 4620.69kb.
- Бенедикт спиноза избранные произведения в двух томах том, 8400.08kb.
- А. Н. Леонтьев Избранные психологические произведения, 6448.08kb.
- Вычислительного Центра Академии наук СССР (вц ан ссср) положило начало истории нашего, 230.29kb.
- А. Н. Леонтьев Избранные психологические произведения, 6931kb.
- Основание Петербургской академии наук, 49.85kb.
401
звезда не поднимается даже до 31 полудиаметра; значит, недостаточно исправления в 10 мин. при 14 мин.
BD Хорда 8142 43235
BDC Синус 43235 8142
BCD Синус 407 86470
172940
43235 345880
116 i 3520 | 19370 4
В пятом примере автора синусы и хорда, как вы видите, та-
ковы
97998
4034
391992 293994 391992 27~
I 3953 1058 3
BD Хорда 4034 ВВС Синус 97998 BCD Синус 1236
145
23932
Параллакс равен 0 гр. 42 мин. 30 сек, он определяет высоту звезды примерно в 4 полудиаметра. Если исправить параллакс, сведя его с 42 мин. 30 сек. только к 5 мин., то и этого нехватит, чтобы поднять звезду даже до 28 полудиаметров. Значит, поправка на 37 мин. 30 сек. мала.
В шестом примере хорда, синусы и параллакс таковы:
BD Хорда
ВВС Синус
BCD 8 мин. Синус
1920 40248 40248 1920
233 804960 362232 40248
26
29 1 772 | 76160 198 1
Звезда оказывается на высоте около 4 полудиаметров. Посмотрим, где она будет, если уменьшить параллакс с 8 до одной только минуты. По этому подсчету и звезда поднялась только приблизительно до 27 полудиаметров! Значит, недостаточно исправления на 7 мин. при 8 мин.
2<э Галилео Галилей, т. I
402
В восьмом примере хорда, синусы и параллакс, как вы видите, таковы 13:
36643 1804
BD Хорда 1804 ВВС Синус 36643 29
BCD Синус
146572 293144 36643
03972
22
29
[ 661 83 2
отсюда автор вычисляет высоту звезды в 1V2 полудиаметра при параллаксе в 43 мин.; если свести его к 1 мин., то все же он даст нам удаленность звезды меньше, чем на 24 полудиаметра; значит, исправления на 42 мин. недостаточно.
Рассмотрим теперь девятый пример. Вот хорда, синусы и параллакс, равный 15 мин. Отсюда автор вычисляет, что удаленность звезды от поверхности Земли была меньше одной сорок седьмой полудиаметра. Но это — ошибка в вычислении, так как на самом деле она, как мы видим здесь рядом, больше одной пятой; получается около 9%зб» что больше одной пятой:
BD Хорда 232 ВВС Синус 39046 BCD Синус 436
39046 232 78092 117138 78092
436 (90 | 58672
То, что добавляет потом автор во исправление наблюдений, т. е. что недостаточно уменьшить разность параллакса не только до 1 мин., но даже восьмой части 1 мин.,— правильно. Но я говорю, что даже и десятая часть 1 мин. не сведет высоту звезды к 32 полудиаметрам; действительно, синус десятой части 1 мин., т. е. 6 сек., равен 3; если на него по нашему правилу мы разделим 90, или, лучше сказать, если мы разделим 9058672 на 300000, то получим 3058672/iooooo> или немногим больше 30 с половиной полудиаметров 14.
Десятое вычисление даст высоту звезды в одну пятую полудиаметра при таких углах, синусах и параллаксе, равном 4 гр. 30 мин. Я вижу, что сведенный с 4 гр. 30 мин. к 2 мин., он не отодвинет звезду даже до 29 полудиаметров.
ДЕНЬ ТРЕТИЙ
403
Хорда
Синус
4 гр. 30 мин. Синус
1746 1746
92050 92050
7846 87300
3492 15714
58
27
1607
441
4
'Одиннадцатое вычисление дает автору звезду на удалении около 13 полудиаметров при параллаксе в 55 мин. Сведя его к 20 ]мин., посмотрим, куда поднимется звезда. Вот вычисление: оно повышает ее немного меньше, чем до 33 полудиаметров; итак, исправление составляет немного меньше 35 мин. при параллаксе в 55 мин.
BD
BDC
BCD
О гр, 55 мин.
| Хорда 19748 Синус 96166 Синус 1600 582 | 96166 19748 |
| 769328 384664 673162 865494 96166 | |
| 32 18990 1536 36 | 86168 |
Двенадцатое вычисление при параллаксе в 1 гр. 36 мин. относит звезду на высоту меньше, чем 6 полудиаметров; если уменьшить параллакс до 20 мин., то звезда оказывается удаленной меньше, чем на 30 полудиаметров; итак, поправки на 1 гр. 16 мин. недостаточно.
BD ВВС
BCD 1 гр. 36 мин.
Хорда Синус Синус
17258 *
96160
2792
17258 96160 8629Ю 17258 103548 155322
582
28
16593
4957
29
56700
Доляшо быть 17258.— См. Орзче, VII, стр. 334.
ДИАЛОГ О ДВУХ ГЛАВНЕЙШИХ СИСТЕМАХ МИРА
Вот поправки параллаксов 10 вычислений автора, которые необходимы, чтобы поместить звезду на высоте 32 полудиаметров
4 гр.
30 сек. при
| | 10 | » — |
| | 37 | » — |
| | 7 | » |
| | 42 | » — • |
| | 14 | » 30 сек. |
| 4 » | 28 | » — • |
| | 35 | » — • |
| 1 » | 16 | » — • |
| | 216 | |
| | 540 | |
| | 756 | |
| 4 гр. | 42 | мин. 30 сек. |
| | 10 | . — - |
| | 14 | — . |
| | 42 | 30 сек. |
| | 8 | — |
| | 43 | . — . |
| | 15 | __ |
| 4 » | 30 | — |
| | 55 | _ |
| 1 » | 36 | — |
| | 296 | 60 |
| | 540 | 9 |
| | 836 | 540 |
Отсюда видно, что для того чтобы поднять звезду на высоту 32 полудиаметров, нужно из суммы параллаксов 836 вычесть 756 и свести ее к 80; но даже и этой поправки недостаточно.
Отсюда явствует (как я только что отметил), что если бы автор пожелал установить истинное местоположение новой звезды на расстоянии 32 полудиаметров, то поправка в остальных его 10 исследованиях (я говорю 10, так как второе, помещая звезду чрезвычайно высоко, сводит ее к удалению на 32 полудиаметра при поправке в 2 мин.) для того, чтобы все они поместили звезду на этом расстоянии, потребовала бы такого уменьшения параллаксов, что все вычеты составили бы больше 756 мин.; в то же время в 5 случаях, вычисленных мною, помещающих звезду выше Луны, для исправления их так, чтобы все они помещали ее на небесном своде, достаточно поправки всего на 10 с четвертью минут. Теперь прибавьте к этим исследованиям еще и другие 5, помещающие звезду как раз на небесном своде без необходимости прибегать к каким-либо поправкам. Тогда мы получим 10 исследований, согласно помещающих звезду на небесном своде с исправлением только 5 из них (как вы видели) на 10 с четвертью минут. В то же время для исправления других 10 исследований автора, чтобы отнести звезду на высоту 32 полудиаметров, нужно сделать поправку на 756 мин. при 836 мин., т. е. нужно из суммы 836 вычесть 756, если мы хотим поднять звезду на высоту 32 полудиаметров, но даже и такой поправки недостаточно.
ДЕНЬ ТРЕТИЙ
405
Те 5 исследований, которые непосредственно, без всяких поправок, дают звезду без параллакса и тем самым относят ее на не-бесный'свод и даже в наиболее удаленные его части, словом, помещают ее на высоте самого полюса, суть следующие:
52 гр. 24 мин. Высота 51 гр. 24 мин.
полюса Огр. 30~м1гйТ
80 гр. 26 мин. 79 гр. 26 мин.
Высота звезды \ j_
О
30 мин.
79 гр. 30 мин.
76 гр. 34 мин.
2 гр. 56 мин.
84 гр.
79 гр. 56 мин. 4 гр. 4 мин.
79 гр. 30 мин.
76 гр. 34 мин.
2 гр. 56 мин.
24 гр. 17 мин.
20 гр. 15 мин.
4 гр. 2 мил.
Высота полюса
Ландграф Хайнцель
Высота звезды
51 гр. 18 мин. 48 гр. 22 мин.
2 гр. 56 мин.
55 гр. 58 мин.
Тихо Пеукер
Рейнгольд Хайнцель
Высота звезды
Высота 51 гр. 54 мин.
полюса 4 гр 4
51 гр. 18 ..
Высота 48 гр. 22 мин. Высота звезды
полюса ~2 гр. 56 мин. !
52 гр. 24 мин
Камерарий Хачек
Высота 48 гр. 22 мин. [ Высота звезды
полюса -4lTTlS: '
Вообще среди попарных сочетаний, которые могут быть сделаны из наблюдений всех этих астрономов, те, которые помещают звезду чрезвычайно высоко, гораздо более многочисленны; их примерно на 30 более, чем других, помещающих звезду согласно вычислениям ниже Луны. Как мы уже согласились, можно ожидать со стороны исследователей скорее меньших, чем больших ошибок, и совершенно очевидно, что значительно меньшие поправки требуется внести в наблюдения, дающие для звезды бесконечную высоту, для помещения звезды на небесном своде, чем в подлунной области. Таким образом, все эти изыскания говорят в пользу мнения тех, кто помещает звезду среди неподвижных звезд. Добавьте, что поправки, которые вносятся для подобных исправлений, значительно меньше тех, посредством которых звезда из неправдоподобной близости может быть отнесена на высоту, наиболее благоприятную для этого автора, как мы видели, на предыдущих примерах; из них невозможную близость дают 3, так как они отодвигают звезду от центра Земли на расстояние, меньшее одного полудиаметра, заставляя ее вращаться некоторым образом под Землею; это такие комбинации, в которых высота полюса одного из наблюдателей больше высоты полюса другого наблюдателя, высота же звезды определена первым меньшей, чем
406 ДИАЛОГ О ДВУХ ГЛАВНЕЙШИХ СИСТЕМАХ МИРА
высота звезды, установленная вторым. Такие комбинации отмечены здесь рядом.
Первая из них — это Ландграф и Гемма; здесь высота полюса у Ландграфа — 51 гр. 18 мин. — больше высоты полюса у Геммы — 50 гр. 50 мин.; но высота звезды у Ландграфа — 79 гр. 30 мин. — меньше высоты звезды у Геммы — 79 гр. 45 мин.
Ландграф Высота 51 гр. 18 мин.\ п / 79 гр. 30
Гемма полюса 50 гр. 50 мин./ Ьысота звезды | ?д гр 45
Две другие таковы:
Буш \ Высота 51 гр. 10 штЛ R ™р--.н / 79 гр< 20 мин'
Гемма / полюса 50 гр. 50 мин./ Ьысота зве*ды | 79 гр 4-
Рейнгольд \ Высота 51 гр. 18 мин Л R„„nT„
Гемма / полюса 59 гр. 50 мин./ ьысота
Из того, что я до сих пор вам показал, вы можете понять, насколько этот первый способ определения удаленности звезды и доказательства ее нахождения ниже Луны, применяемый автором, не благоприятствует его цели и насколько более вероятным представляется, что звезда находилась на расстоянии самых далеких неподвижных звезд 1Г>.
С и м п л и ч и о. Пока что, мне кажется, с совершенной очевидностью раскрыта несостоятельность доводов автора; но я вижу, что все это изложено на немногих страницах книги; другие его соображения, может быть, более доказательны, чем первые.
С а л ь в и а т и. Напротив, они могут быть только еще менее убедительными, если считать, что первые являются примером для остающихся; совершенно ясно, что недостоверность и слабая убедительность их (как мы хорошо это понимаем) происходят от ошибок, вкравшихся в наблюдения при посредстве инструментов; считалось, что высоты полюса и звезды были определены точно, тогда как на самом деле все эти определения легко могли быть ошибочными, хотя для определения высоты полюса астрономы располагали столетиями, чтобы заниматься этим на свободе; высоты же звезды при прохождении через меридиан наиболее удобны для наблюдения, так как они вполне отчетливы и допускают некоторую свободу для наблюдателя, в смысле продолжительности наблюдения благодаря менее ощутимым изменениям за очень короткий промежуток времени чем, то бывает со звездами, удаленными от меридиана. Но если это так, — а это самая подлинная истина, — то как можем мы верить вычислениям, основанным на более многочисленных и более трудных для выполнения наблю-
ДЕНЬ ТРЕТИЙ
407
пениях над предметами, более быстро изменяющимися, вдобавок при применении инструментов, более неудобных и менее точных? Из беглого просмотра последующих доказательств я увидел на определении высот звезд, взятых в разных вертикальных кругах, называемых арабским словом азимут; при этих наблюдениях применяются инструменты, способные перемещаться не только в вертикальной плоскости, но в то же самое время и в горизонтальной; нужно в тот же самый момент, когда определяется высота над горизонтом, наблюдать и расстояние от меридиана того вертикального круга, на котором находится звезда. Кроме того, через определенный промежуток времени нужно повторить это наблюдение и тщательно учесть протекшее время, полагаясь на часы или другие наблюдения над звездами. Такая группа наблюдений сопоставляется потом с другой такой же группой, полученной другим наблюдателем, в другой стране, другими инструментами и в другое время, и из этого автор пытается извлечь познание того, каковы были высоты и горизонтальные широты звезды во время и час других — первых — наблюдений; на созданном таким образом основании он проделывает напоследок свои вычисления. Теперь я предоставляю судить вам самим, насколько можно доверять тому, что получается из подобных сопоставлений. Кроме того, я ничуть не сомневаюсь, что если бы кто-нибудь захотел потрудиться над такими длиннейшими вычислениями, то нашлось бы, как и раньше, больше таких, которые благоприятствуют противной стороне, а не автору; но мне кажется, не стоило -браться за подобный труд ради того, что не составляет самого главного в интересующем нас вопросе.
Сагредо. В этом я с вами согласен, однако, если подобное предприятие окружено такой путаницей, недостоверностью, ошибками, то на основании чего столь многие астрономы решительно провозгласили, что новая звезда находилась чрезвычайно высоко?
Сальвнати. На основании двоякого рода наблюдений, чрезвычайно простых, чрезвычайно легких и совершенно истинных; одного из них вполне достаточно, чтобы убедить нас в том, что звезда помещалась на небесном своде или по крайней мере гораздо выше Луны. Одно заключается в равенстве или весьма малой разнице ее удаленности от полюса как тогда, когда она находилась в нижней части меридиана, так и тогда, когда она была в верхней его части. Другое — это то, что она постоянно сохраняла одинаковые расстояния от некоторых неподвижных звезд, к ней близких, в частности от одиннадцатой звезды Кассиопеи, удаленной от нее не больше, чем на полтора градуса 16; из этих
408
ДИАЛОГ О ДВУХ ГЛАВНЕЙШИХ СИСТЕМАХ МИРА
двух главных положений с несомненностью вытекает или абсолютное отсутствие параллакса, или такая его незначительность, которая убеждает нас после чрезвычайно быстро выполняемых вычислений в ее огромной удаленности от Земли.
С а г p e д о. Но разве это не было принято во внимание автором? А если он это видел, то как он от этого оборонялся?
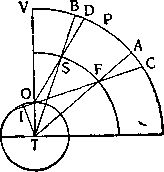
Сальвиати. Когда кто-нибудь, не находя лучших отговорок, способных покрыть его промахи, приносит легкомысленные извинения, мы обычно говорим, что он пытается ухватиться за веревку с неба; но этот автор прибегает даже не к веревкам, а к паутинкам с неба. Вы ясно увидите это, если рассмотрите два обстоятельства, которые я сейчас вам укажу. Прежде всего, то, что нам показывают полярные расстояния каждого из наблюдателей, я отметил здесь в этих кратких вычислениях; для полного понимания их я прежде всего должен заметить вам, что каждый раз, как новая звезда или иное небесное явление будет близко к Земле, вращаясь суточным движением вокруг полюса, оно покажется более отдаленным от него тогда, когда оно находится в нижней части меридиана, чем когда оно находится в верхней его части, как это видно на следующем чертеже: здесь точка Т обозначает центр Земли, О —место наблюдателя, дуга VPC — небесный свод, P — полюс. Явление, двигаясь по кругу FS, видно то под полюсом по лучу OFC, то над ним по лучу OSD, так что места, видимые на небесном своде, будут D и С. Но истинные места, по отношению к центру Г,— это А и В, равноудаленные от полюса; отсюда уже ясно, что видимое место небесного явления S, т. е. точка D, ближе к полюсу, чем другое видимое место С, наблюдаемое по лучу OFC\ это нужно заметить прежде всего. Во-вторых, вам следует заметить, что превышение нижнего видимого расстояния от полюса над верхним видимым расстоянием также от полюса больше, чем нижний параллакс явления; другими словами; превышение дуги С P (нижнего видимого расстояния) над дугой PD (верхним видимым расстоянием) больше, чем дуга СА (нижний параллакс). Это легко доказывается: ведь дуга СР превышает PD на большую величину, чем РВ, так как P В больше PD\ но РВ равно РА, и превышение СР над РА составляет дугу С А] следовательно, превышение дуги СР над дугой PD больше дуги С А, т. е. больше параллакса небесного явления, находящегося в F; это и требовалось доказать.
ДЕНЬ ТРЕТИЙ 409
Чтобы предоставить теперь все преимущества автору, предположим, что параллакс звезды в F составляет все превышение дуги СР (т. е. нижнего расстояния от полюса) над дугой PD (верхним расстоянием). Отсюда я перехожу к изучению того, что нам дают наблюдения всех астрономов, приведенных автором; среди них нет ни одного, которое было бы в его пользу и которое не противоречило бы его намерению 17.
Начнем с наблюдений Буша; он нашел, что верхнее расстояние звезды от полюса равно 28 гр. 10 мин., а нижнее — 28 гр. 30 мин., так что превышение составляет 0 гр. 20 мин.; примем (в пользу автора), что все оно составляет параллакс звезды в F, т. е. угол TFO\ расстояние от вертикали, т. е. дуга CV, составляет 67 гр. 20 мин. Найдя две эти величины, продолжим линию СО, опустим на нее перпендикуляр TI и рассмотрим треугольник ТО/; в нем угол / — прямой, угол ЮТ известен, так как он равен углу У ОС, т. е. расстоянию звезды от вертикали; кроме того, в треугольнике TIF, также прямоугольном, известен угол F, принятый за параллакс. Итак, пометим в стороне величины углов ЮТ и IFT и по ним определим синусы, которые, как вы видите, здесь и отмечены 18. И так как в треугольнике ЮТ весь синус ТО состоит из 100000 таких частей, каких синус TI содержит 92276, а в треугольнике IFT синус TF состоит из 100000 таких частей, каких в синусе TI содержится 582, то чтобы найти, сколько в TF будет таких частей, каких в ТО содержится 100000, скажем, по золотому правилу: если TI равно 582, то TF равно 100000; но если TI равно 92276, то каково будет TF1 Множим 92276 на 100000 и получаем 9227600000; ото число нужно разделить на 582; получим как это видно, 15854982; в TF будет, следовательно, именно столько таких частей, каких в ТО содержится 100000. Теперь, чтобы узнать, сколько отрезков ТО содержится в TF, разделим 15854982 на 100000; получим приблизительно 158 с половиной; столько именно полудиаметров составляет расстояние звезды F от центра Т. А чтобы сократить действие, поскольку произведение от умножения 92276 на 100000 нам нужно было делить сначала на 582, а потом частное на 100000, мы можем, не умножая 92276 на 100000, одним лишь делением синуса 92276 на синус 582 быстро получить то же самое, как это видно здесь ниже, где 92276, деленное на 582, даст нам то же самое — приблизительно 158 с половиной. Запомним, следовательно, что одно только деление синуса TJ', как синуса угла Т01, на синус TI, как синус угла /FT, дает нам искомое расстояние TF в полудиаметрах ТО,
410
ДИАЛОГ О ДВУХ ГЛАВНЕЙШИХ СИСТЕМАХ МИРА
| Углы | / ЮТ \ IFT | 67 гр. 0 гр.' | 20 мин.\ 20 мин./ | синусы / 92276 15854982 иинусы | 582 582 9227600000 | |
| | TI | TF | TI TF 34( | )7002246 | |
| | 582 | 100000 | 92276 0 49297867 | ||
| | | | | | 325414 |
| | | | | 100000 | 15£ | 54982 |
| | | | | | 158 |
| | | | | 582 | i 92276 |
| | | | | | 34070 |
| | | | | | 492 |
| | | | | | 3 |
Посмотрим теперь, что нам дают наблюдения Пеукера. У него нижнее расстояние от полюса равно 28 гр. 21 мин., верхнее — 28 гр. 2 мин. разность — 0 гр. 19 мин., расстояние от вертикали — 66 гр. 27 мин.; из этих данных легко получается, что расстояние звезды от центра равно почти 166 полудиаметрам.
УПЫ / 1АС 66
