Академия наук СССР галилео галилей избранные труды в двух томах

Вид материала

Документы

Содержание Мин' 1 синусы / Диалог о двух День третий 413 414 Диалог о двух главнейших системах мира День третий 416 Диалог о двух главнейших системах мира День третий Объемлющему и объ-емлемому более под­ходит вращаться вокруг одного и того же центра, "нежели вокруг разных. 418 Диалог () двух главнейших системах мира День третий Диалог о двух главнейших системах мира Марс в]протшосто-янии с Солнцем ка­жется в 60 раз большим, чем в соединении. День третий 421

Подобный материал:

• Галилео галилей (Galilei), 238.2kb.
• Галилей галилео галилей галилео, 23.36kb.
• Жизнь и деятельность Галилео Галилея, 159.16kb.
• Галилео Галилей (1564-1642), 46.37kb.
• Отечества избранные психологические труды в 70-ти томах, 4620.69kb.
• Бенедикт спиноза избранные произведения в двух томах том, 8400.08kb.
• А. Н. Леонтьев Избранные психологические произведения, 6448.08kb.
• Вычислительного Центра Академии наук СССР (вц ан ссср) положило начало истории нашего, 230.29kb.
• А. Н. Леонтьев Избранные психологические произведения, 6931kb.
• Основание Петербургской академии наук, 49.85kb.

Т АС 66

₍₎

57 мин. g _юш
f_v

(Углы _1ЕС

.\ p „ Г _>| Синусы (

92012

_{8? 8?}

Взяв у Камерариядва из его наблюдений, наиболее благопри­ятных для автора, находим удаленность звезды от центра в 3143 полудиаметра.


'> Синусы I
Углы

1 АС 65 гр. 43 мин. l ЕС О гр. 1 мин

91152 29

29

3143

91152

4295

1

ДИАЛОГ О ДВУХ ГЛАВНЕЙШИХ СИСТЕМАХ МИРА

расстояния оказываются правильными и точными, а не видимыми и ложными. Если же он думает, что такие авторы не задумыва­лись над рефракцией, то, нужно признать, все они одинаково ошибались в определении всех тех вещей, которые не могут быть в совершенстве установлены, без учета изменений в силу рефрак­ции; одна из таких вещей — это точное установление высот по­люса, которые обычно определяются из двух меридианных высот какой-нибудь незаходящей неподвижной звезды; эти высоты изме­няются рефракцией совершенно так же, как высоты новой звезды; таким образом высота полюса, которая из них выводится, оказы­вается ошибочной и причастной тому же самому недостатку, ко­торый этот автор приписывает высотам, установленным для но­вой звезды, т. е. и высота полюса, и высота новой звезды, благо­даря одинаковым ошибкам, оказываются выше, чем в действи­тельности. Но такая ошибка, поскольку она относится к раз­бираемому нами теперь вопросу, вовсе не вредит, ибо раз нам нужно знать только разность между двумя расстояниями новой звезды от полюса,— когда она ниже и когда выше его,— то ясно, что такие расстояния будут теми же самыми, оставим ли мы иска­жение, вносимое рефракцией, общее для звезды и для полюса, или же внесем поправки, одинаковые в обоих случаях. Некоторую силу, хотя и чрезвычайно слабую, имел бы аргумент автора, если бы он доказал нам, что высота полюса была установлена точно и освобождена от ошибок, связанных с рефракцией, но этого не было сделано теми же самыми астрономами при установлении высоты новой звезды; однако он не ручается нам за это, может быть, потому, что не может этого сделать, а может быть, потому (и это более вероятно), что такая предосторожность не была при­нята наблюдателями.

С. а г p e д о. Мне кажется, что это положение целиком унич­тожено; поэтому скажите мне, как же он справляется с тем, что новая звезда всегда сохраняла одно и тоже расстояние от окру­жающих ее неподвижных звезд?

G а л ь в и а т и. Попросту хватаясь за две нити, еще более слабые. Одна из них также связана с рефракцией, но еще менее прочна, поскольку он говорит, что рефракция, воздействуя на ви­димость новой звезды и поднимая ее выше ее настоящего места, делает недостоверным расстояние, принимаемое за истинное, по отношению к соседним с нею неподвижным звездам. Я не могу в достаточной мере надивиться, как он притворяется невидящим, что та же самая рефракция будет воздействовать одинаково как на новую звезду, так и на соседнюю старую, одинаково поднимая

ДЕНЬ ТРЕТИЙ 413

их обе так что от этого обстоятельства расстояние между ними не изменится. Другое прибежище еще менее удачно и просто смехо­творно; оно заключается в ссылке на ошибку, которая может возникнуть при пользовании инструментами ²⁰, так как наблю­датель не может установить центр зрачка в центре секстанта (ин­струмента, употребляемого при наблюдении расстояний между двумя звездами) и вынужден держать его выше этого центра на расстоянии зрачка не знаю уже от какой скулы, к которой прик­ладывается головка инструмента, то угол с вершиной в зрачке оказывается более острым, чем тот, который образован сторона­ми секстанта. Но ведь этот угол зрительных лучей меняется и сам по себе, если рассматривать сперва звезды, мало возвышающиеся над горизонтом, а затем их же, когда они поднялись на значитель­ную высоту. Этот угол меняется, говорит он, если поднимать инструмент и держать голову неподвижной; если же при подни­мании секстанта сгибать шею назад и откидывать голову вместе с инструментом, то угол сохранится тем же самым. Итак, возра­жение автора основано на предположении, что при употреблении инструмента наблюдатели поднимали голову не так, как это было нужно, что является вещью невероятной. Но предположив даже, что это было так, я предоставляю вам судить, какова может быть разность между двумя острыми углами двух равнобедренных тре­угольников, если стороны одного из них будут длиною в четыре локтя каждая, а стороны другого меньше четырех локтей на диа­метр хрусталика; больше во всяком случае не может быть разни­ца между длиной двух зрительных лучей, если в одном случае линия опускается перпендикулярно из центра зрачка на пло­скость оси секстанта (длина этой линии не превышает толщины большого пальца), и длиною тех же лучей, если в другом случае при поднимании секстанта не поднимать одновременно с ним го­ловы, так что такая линия больше не будет перпендикулярна к этой плоскости, но отклонится в сторону, образуя с ней острый угол. Чтобы совершенно покончить с этими злосчастными и жал­кими попытками автора, скажу следующее: пусть он знает (ибо, как видно, он не очень опытен в употреблении астрономических инструментов), что по сторонам секстанта или квадранта устраи­ваются два визира — один в центре, другой. — на противопо­ложном конце; они отстоят на дюйм или больше от плоскости, и через верхние края таких визиров должен проходить луч зрения. Глаз также держится на расстоянии пяди или двух или еще даль­ше от инструмента, так что ни зрачок, ни скула, ни вся особа астронома не касается инструмента и не опирается на него; тем

414 ДИАЛОГ О ДВУХ ГЛАВНЕЙШИХ СИСТЕМАХ МИРА

менее этот инструмент поддерживается или поднимается руками, в особенности, если это один из тех обычных больших инструмен­тов, которые весят десятки, сотни или даже тысячи фунтов и уста­навливаются на чрезвычайно солидных фундаментах. Таким об­разом, все построение рассыпается. Таковы доводы этого автора. И если бы даже они были столь же несокрушимы, как сталь, они не могли бы принести ему подъема и на одну сотую часть минуты, а он думает, будто убедил нас в том, что ими он скомпенсировал ту разность, которая составляет сто и больше минут. Я говорю, что не наблюдалось заметного различия в расстояниях между какой-либо неподвижной звездой и новой звездой за все время их суточного обращения, а если бы звезда находилась примерно на расстоянии Луны, то различие должно было бы быть очень замет­ным даже для простого глаза, без какого бы то ни было инстру­мента, в особенности при сопоставлении ее с одиннадцатой звез­дой Кассиопеи, удаленной всего на полтора градуса; различие в расстоянии должно было бы меняться больше, чем на два лунных диаметра, как это было отмечено наиболее знающими астрономами того времени.

С а г p e д о. Мне кажется, что я вижу несчастного земле­дельца, который после того, как буря повалила и уничтожила весь его долгожданный урожай, идет с понурым лицом, собирая по зер­нышку такие ничтожные остатки, что их ему не хватит даже на прокормление цыпленка в течение одного-единственного дня.

С а л ь в и а т и. Действительно, слишком плохо вооружен­ным поднялся этот автор против тех, кто оспаривает неизменность неба, и слишком слабыми цепями пы-тался он совлечь новую звез­ду в созвездии Кассиопеи с самых высоких областей в низкие области стихий. Теперь, после того как, мне кажется, очень ясно была показана огромная разница между аргументами астрономов и этого их противника, хорошо было бы вернуться к нашей основ­ной теме. Здесь нам следует обсудить годовое движение, которое обычно приписывается Солнцу, но которое сначала Аристарх Са-мосский, а затем Коперник отнимают у Солнца и переносят на Землю. Против такого положения, я чувствую, будет доблестно выступать синьор Симпличио, вооруженный мечом и щитом из его книжки с выводами или математическими исследованиями: хорошо было бы начать с этих возражений.

.Симпличио. Я предпочел бы с вашего позволения сохра­нить их напоследок, так как и открыты они были последними.

Сальвиати. Итак, соответственно применявшемуся до сих пор методу вам следует по порядку изложить соображения

ДЕНЬ ТРЕТИЙ

415


416 ДИАЛОГ О ДВУХ ГЛАВНЕЙШИХ СИСТЕМАХ МИРА

Симпличио. Аристотель приводит сотню доказательств того, что мир конечен, ограничен и сферичен.

Сальвиати. Но все его доказательства сводятся к одно-

Ултштеая^Пвапри- ^мУ~^еД^{инственн}ому, а это одно-единственное обращается в ничто;

водимые в пользу ко- ведь если я буду отрицать основное его положение, что вселенная подвижна, то все его доказательства отпадут, так как он доказы­вает конечность и ограниченность, исходя только из подвижности вселенной. Но чтобы не умножать споров, допустим пока, что мир конечен, сферичен и имеет собственный центр, а раз и такая фор­ма, и наличие центра выводятся из подвижности, то вполне разум­но, чтобы от тех же самых круговых движений мировых тел мы пришли к особому изучению местонахождения такого центра. Ведь сам Аристотель рассуждал и выводил заключения таким пу­тем, сделав центром вселенной ту точку, вокруг которой врагца-

ту^тточку^в,^се*1^е<°]г ются все небесные сферы, и в которой, как он думал, помещается земной шар. Теперь скажите мне, синьор Симпличио: если бы Аристотель оказался вынужденным очевиднейшими опытами из­менить отчасти это свое построение и распорядок вселенной и

Спрашивается, ка- признать, ЧТО ОН ОШИбаЛСЯ В ОДНОЙ ИЗ ДВух СЛвДуЮЩИХ ПрвДПО-

кую из двух предпо- * ' ⁽_ j

сылок, противореча- сылок, а именно: или в том, что Земля помещается в центре, или

momef^Ho предпо- ^{В ТОМ}' ^ЧТО НвбеСНЫв Сферы ДВИЖУТСЯ ВОКруГ КаКОГО-ТО ЦбНТра, ТО

чел бы,'если бы был какое из этих двух положений, думаете вы, избрал бы он?

вынужден, выбрать •> —, ^{7 А}

одну. Ьимпличио. Думаю, что если бы произошел такой слу-

чай, то перипатетики...

Сальвиати. Я спрашиваю не о перипатетиках, я спра­шиваю о самом Аристотеле; о них-то я прекрасно знаю, что они ответили бы. Они, как почтительнейшие и смиреннейшие слуги Аристотеля, стали бы отрицать все опыты и наблюдения в мире, отказывались бы даже посмотреть их, чтобы не оказаться вынуж­денными их признать, и сказали бы, что мир устроен так, как пи­шет Аристотель, а не так, как хочет природа; ведь, если отнять у них поддержку такого авторитета, то с чем появятся они на • поле сражения? А потому скажите мне, что, по вашему мнению, сделал бы сам Аристотель?

Симпличио. Право, я не знаю, какую из двух несообраз­ностей он счел бы меньшей.

Сальвиати. Не пользуйтесь, пожалуйста, этим термином и не называйте несообразностью то, что должно быть по необхо­димости. Несообразностью было бы стремление помещать Землю в центре небесных обращений. Но раз вы не знаете, в какую сто­рону склонился бы Аристотель, то, считая его за человека вели­кого ума, посмотрим, какой выбор из двух предпосылок является

ДЕНЬ ТРЕТИЙ


наиболее разумным, и будем считать его за сделанный Аристо­телем. Итак, начнем опять наше рассуждение сначала и примем ради Аристотеля, что мир (о величине которого, кроме неподвиж­ных звезд, у нас нет никаких доступных чувству показаний) есть нечто такое, что имеет сферическую форму и движется кругооб­разно и по необходимости имеет,— принимая во внимание фор­му и движение,— центр; а так как, кроме того, мы достоверно зна­ем, что внутри звездной сферы существует много орбит, одна внутри другой, с соответствующими звездами, которые также движут­ся кругообразно, то спрашивается, чему более разумно верить и что более разумно утверждать: то ли, что эти внутренние орбиты движутся вокруг одного и того же мирового центра, или же что они движутся вокруг другого, очень далекого от первого? Ска­жите теперь, синьор Симпличио, каково ваше мнение на этот счет?

С и м п л и ч и о. Если бы мы могли остановиться на этом од­ном предположении и если бы мы были уверены, что не встретим еще каких-либо новых затруднений, я сказал бы, что гораздо разумнее признать, что и включающее и включенные части дви­жутся вокруг одного общего центра, чем вокруг разных центров.

С а л ь в и а т и. Значит, если правильно, что центром мира является точка, вокруг которой движутся орбиты небесных тел, т. е. планет, то гораздо более правдоподобно, что не Земля, а Солн­це находится в центре мира. Таким образом, соответственно это­му первому простому и общему положению, место в центре свой­ственно Солнцу, а Земля находится столь же далеко от центра, как и от Солнца.

Симпличио. Но из чего вы заключаете, что не Земля, а Солнце находится в центре обращения планет?

С а л ь в и а т и. Это следует из очевиднейших и потому не­избежно доказательных наблюдений. Наиболее убедительным для удаления Земли из такого центра и помещения в нем Солнца является то, что все планеты находятся то ближе, то дальше от Земли, причем разность так велика, что, например, Венера в са­мом далеком положении находится в шесть раз дальше от нас, чем когда она в самом близком положении, а расстояние Марса при одном положении почти в восемь раз больше, чем при другом. Вы видите, таким образом, что Аристотель немного ошибся, ду­мая, что они всегда одинаково удалены от нас.

Симпличио. Но каковы признаки того, что движения их совершаются вокруг Солнца?

Сальвиати. Относительно трех верхних планет — Мар­са, Юпитера и Сатурна — это доказывается тем, что они особен-

27 Галилео Галилей, т. I

Объемлющему и объ-емлемому более под­ходит вращаться вокруг одного и того же центра, "нежели вокруг разных.

Если центр вселен­ной совпадает с точ­кой, вокруг которой движутся планеты, то в нем находится Солнце, а не Земля.

Наблюдения, из ко­торых можно за­ключить, что С< ли­пе, а не Земля рас­положено в центре небесных обрашении.

418 ДИАЛОГ () ДВУХ ГЛАВНЕЙШИХ СИСТЕМАХ МИРА

но близки к Земле, когда находятся в противостоянии с Солнцем, и особенно далеки, когда находятся в соединении; это приближе­ние и удаление настолько значительны, что Марс вблизи виден в 60 раз большим, чем когда он очень далек ²³. Что Венера и Мер-

иенеры^Н"докаашвает ^КУР^ИИ обращаются ВОКруТ СоЛНЦа, убеждает 1ШС ТО, ЧТО ОНИ II|[-движение ее вокруг КОГДа Н6 удаЛЯЮТСЯ ОТ Н6ГО НаМНОГО И ВИДНЫ ТО ПврбД НИМ, ТО

^олнца- позади него, как это необходимо следует из изменения формы

луна не может от- ^енеР^ы '• Что касается Луны, то по основаниям, которые более делиться от Земли, подробно будут развиты впоследствии, она на самом деле никоим образом не может отделиться от Земли.

С а г p e д о. Как видно, в связи с годовым движением Земли мне придется выслушать вещи, гораздо более удивительные, чем в связи с суточным движением.

С а л ь в и а т и. Вы нисколько не ошибаетесь; ведь в отно­шении суточного движения небесных тел не существует и не мо­жет быть наблюдаемо ничего другого, кроме того, что заставляет

ЗечТиТ'соединении ^{Б6СЬ МП}Р ^{казаться} ДВИЖУЩИМСЯ С НвВврОЯТНОЙ СКОРОСТЬЮ В обрат-

с движением других ном направлении; но годовое движение, сочетаясь с частными

планет вызывает

удивительные явле- движениями всех планет, порождает многочисленные странно-
^ния- сти, которые до сих нор сбивали с толку величайших на свете

мудрей. Но возвращаясь к первым общим допущениям, я повто­ряю, что центром небесных обращений пяти планет — Сатурна, Юпитера, Венеры, Марса и Меркурия — является Солнце; оно же будет и центром движения Земли, если нам удастся по­местить ее на небо. Что же касается Луны, то она обладает кру­говым движением вокруг Земли, от которой (как я уже сказал) никоим образом не может отделиться, но при этом она не пере­стает двигаться вокруг Солнца вместе с Землей годовым дви­жением.

С и м п л и ч и о. Я еще не очень хорошо уразумел эту струк­тур У J может быть, при помощи маленького чертежа она станет по­нятнее и о ней можно будет легче говорить.

схема устройств С а л ь в и а т и. Пусть будет так; для большего вашего удов-

основипи и летворения и вместе с тем удивления я хочу, чтобы вы сами его нарисовали и увидели, что вы прекрасно понимаете эту структуру, хотя и думаете, что не поняли; только чертите аккуратно в соот­ветствии с ответами на мои вопросы.

Итак, возьмите бумагу и циркуль; пусть этот белый лист будет огромным пространством вселенной, на котором вы должны рас­положить и привести в порядок части вселенной так, как это вам продиктует разум. Прежде всего, раз вы и без моего поучения считаете, что Земля находится в этой вселенной, то отметьте по

ДЕНЬ ТРЕТИЙ

своему усмотрению точку, в которой, как вы полагаете, она по­мещается, и обозначьте ее какой-нибудь буквой.

Симпличио. Пусть А обозначает место земного шара,

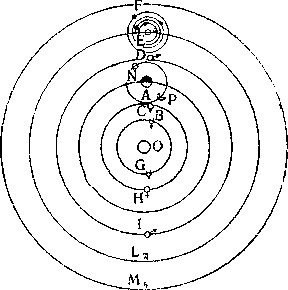
Сальвиати. Хорошо. Во-вторых, как мне известно, вы прекрасно знаете, что Земля находится не внутри солнечного тела и даже не соприкасается с ним, но отстоит от него на некотором рас­стоянии; поэтому отметьте Солнце в каком-либо другом месте, какое вам больше понравится, удален­ном от Земли по вашему усмот­рению, и обозначьте также и его.

Симпличио. Сделано. Пусть место солнечного тела будет обозначено через О.

Сальвиати. Установив эти два места, нам нужно поду­мать, как бы поместить тело Вене­ры таким образом, чтобы поло­жение и движение ее могли удо­влетворить тому, что нам показы­вают воспринимаемые чувствами явления. Поэтому, основываясь на прежних беседах или же на ваших собственных наблюдениях, припомните, что происходит с данной звездой, а потом обозначьте то положение, какое вам покажется подобающим ей.


Венера кажется на«-большей во время ве-чернего и наимень-

Убедительное до-

казательство , того, _что Венера обра-
Симпличио. Если признать истинными описанные вами явления, о которых я читал также в своей книжке, а именно, что эта звезда никогда не удаляется от Солнца больше, чем на неко­торый определенный промежуток, примерно в 40 градусов, так что она никогда не оказывается не только в противостоянии с Солнцем, но и в квадратурах и даже под углом в 60 градусов; далее, если правильно, что она представляется в определенное время почти в 40 раз большей, чем в другое время, именно, особенно велика она тогда, когда движется попятно к вечернему соединению с Солн­цем, и особенно мала, когда движется поступательно к утреннему солнцем, соединению с Солнцем; далее, если правильно, что когда она ка­жется особенно большой, то проявляется в виде другой фигуры, а когда кажется совсем маленькой, то представляется совершенно круглой; если, говорю я, правильны эти явления, то я не вижу, как можно избежать признания, что данная звезда обращается по чается вокруг солн-кругу вокруг Солнца, причем про этот круг никоим образом нель­зя сказать, что он обнимает собою и включает внутри себя Землю,

27*

420

ДИАЛОГ О ДВУХ ГЛАВНЕЙШИХ СИСТЕМАХ МИРА



Доказательство того, что обраще­ние Меркурия во­круг Солнца проис­ходит внутри ор­биты Венеры.

Марс необходимо включает в свою орбиту и Землю, и Солнце.

Марс в]протшосто-янии с Солнцем ка­жется в 60 раз большим, чем в соединении.

Юпитер и Сатурн также охватываю n •Землю и Солнце.

и еще меньше, что он .ниже Солнца, т. е. между ним и Ззмлей, или же выше Солнца. Этот круг не может обнимать Землю, так как тогда Венера должна была бы быть иногда в противостоянии с Солнцем; он не может быть ниже, так как тогда Венера при каждом соединении с Солнцем казалась бы серпообразной; не может он быть и выше, так как тогда она представлялась бы всегда круглой и никогда — двурогой. А потому для ее местонахождения я на­черчу круг СН около Солнца так, чтобы он не захватывал Землю.

Сальвиати. Поместив Венеру, хорошо было бы вам по­думать о Меркурии, который, как вы знаете, всегда держится близко к Солнцу, удаляясь от него еще меньше Венеры; поэтому размыслите, какое место назначить ему.

Симпличио. Несомненно, что раз он подражает Венере, то самым удобным местом для него будет меньший круг, описан­ный также около Солнца, внутри круга Венеры, так как особен­но убедительным доказательством и признаком его чрезвычайной близости к Солнцу служит сила его сияния, превосходящего сия­ние Венеры и других планет; итак, на этом основании мы можем начертить круг для Меркурия и обозначить его буквами BG.

Сальвиати. А куда мы поместим Марс?

Симпличио. Поскольку Марс бывает в противостоянии с Солнцем, он неизбежно должен обнимать своим кругом Землю; но я вижу, что он необходимо должен обнимать также и Солнце, так как если бы при движении к соединению с Солнцем он проходил не за ним, а перед ним, то он оказался бы двурогим, подобно Ве­нере и Луне, а он всегда представляется круглым; необходимо, следовательно, чтобы он включал внутри своего круга не только Землю, но и Солнце. А поскольку, как я припоминаю, вы сказали, что вэ время противостояния с Солнцем он кажется в 60 раз боль­шим, чем во время соединения, то, мне думается, очень хорошо удовлетворит этим явлениям круг около центра Солнца, который обнимает также и Землю; его я начерчу здесь и обозначу через DI; здесь Марс в точке'/) особенно близок к Земле и находится в про­тивостоянии с Солнцем; когда жз он находится в точке /, он в со­единении с Солнцем, но особенно далек от Земли. И так как те же самыз явления наблюдаются у Юпитера и Сатурна, хотя и со зна­чительно меньшими отклонениями у Юпитера, чем у Марса, а у Сатурна ещз меньшими, чем у Юпитера, то мне кажется понятным, что особенно удачно мы удовлетворили бы также и эти две планеты двумя кругами, по-прежнему описанными вокруг Солнца: Юпи­тера — вот этим первым, обозначенным через EL, и Сатурна — другим верхним, обозначенным через

ДЕНЬ ТРЕТИЙ 421

С а л ь в и а т и. До сих пор вы поступали отлично. И раз /«а« ям видите) приближение и удаление трех верхних планет них планет на