Академия наук СССР галилео галилей избранные труды в двух томах
| Вид материала | Документы |
- Галилео галилей (Galilei), 238.2kb.
- Галилей галилео галилей галилео, 23.36kb.
- Жизнь и деятельность Галилео Галилея, 159.16kb.
- Галилео Галилей (1564-1642), 46.37kb.
- Отечества избранные психологические труды в 70-ти томах, 4620.69kb.
- Бенедикт спиноза избранные произведения в двух томах том, 8400.08kb.
- А. Н. Леонтьев Избранные психологические произведения, 6448.08kb.
- Вычислительного Центра Академии наук СССР (вц ан ссср) положило начало истории нашего, 230.29kb.
- А. Н. Леонтьев Избранные психологические произведения, 6931kb.
- Основание Петербургской академии наук, 49.85kb.
из.ю.ю. **±>j ? r i-- j r i j
ЭТО будет Круг, СООТВеТСТВуЮЩИИ На ЗВеЗДЫОИ Сфере КОЛуру СОЛНЦе- emu от их расстоя-
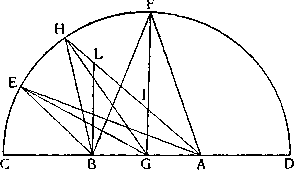
етояния 46; обозначим его СЕН', вместе с тем он будет и меридиа- ния от »клиг>тики-ном; возьмем на нем звезду вне эклиптики; пусть это будет Е. При движении Земли она будет очень сильно менять свою высоту, так как с Земли, находящейся в А, она будет видна в направлении АЕ при высоте, измеряемой углом E АС; но с Земли, находящейся в .В, она будет видна в направлении BE при высоте, измеряемой углом ЕВС; последний больше угла ЕАС, так как он — внешний, а тот — внутренний и противоположный в треугольнике ЕАВ. Таким образом, расстояние звезды E от эклиптики видимо изменится; высота звезды на меридиане при положении Земли в В станет также больше, чем при положении Земли в А, соответственно тому, насколько угол ЕВС превосходит угол ЕАС, т. е. на величину угла АЕВ; ведь если в треугольнике ЕАВ продолжить сторону AB до С, то внешний угол ЕВС (будучи равен сумме внутренних противоположных углов Е и А) превосходит угол А на величину угла Е. Если мы возьмем на том же меридиане другую звезду, но более удаленную от эклиптики, — пусть это будет, например, звезда Я, — то при наблюдении ее с двух мест А и В разница будет еще больше, поскольку угол АНВ делается больше угла при Е; этот угол все время растет в зависимости от все большего удаления наблюдаемой звезды от эклиптики, так что в конце концов наибольшее
изменение проявится в той звезде, которая будет помещаться на самом полюсе эклиптики. Для полного понимания мы Можем доказать это так. Пусть AB будет диаметр земной орбиты, a G ее центр; представим себе диаметр продолженным до звездной сферы в точках D и С и пусть из центра G проведена перпендикулярно плоскости эклиптики ось GF, продолженная до той же сферы; предположим, что на ней же расположен меридиан DFC, перпендикулярный к плоскости эклиптики; взяв на дуге FC любые точки ff и Е, как места неподвижных звезд, проводим
ЭТО будет Круг, СООТВеТСТВуЮЩИИ На ЗВеЗДЫОИ Сфере КОЛуру СОЛНЦе- emu от их расстоя-

етояния 46; обозначим его СЕН', вместе с тем он будет и меридиа- ния от »клиг>тики-ном; возьмем на нем звезду вне эклиптики; пусть это будет Е. При движении Земли она будет очень сильно менять свою высоту, так как с Земли, находящейся в А, она будет видна в направлении АЕ при высоте, измеряемой углом E АС; но с Земли, находящейся в .В, она будет видна в направлении BE при высоте, измеряемой углом ЕВС; последний больше угла ЕАС, так как он — внешний, а тот — внутренний и противоположный в треугольнике ЕАВ. Таким образом, расстояние звезды E от эклиптики видимо изменится; высота звезды на меридиане при положении Земли в В станет также больше, чем при положении Земли в А, соответственно тому, насколько угол ЕВС превосходит угол ЕАС, т. е. на величину угла АЕВ; ведь если в треугольнике ЕАВ продолжить сторону AB до С, то внешний угол ЕВС (будучи равен сумме внутренних противоположных углов Е и А) превосходит угол А на величину угла Е. Если мы возьмем на том же меридиане другую звезду, но более удаленную от эклиптики, — пусть это будет, например, звезда Я, — то при наблюдении ее с двух мест А и В разница будет еще больше, поскольку угол АНВ делается больше угла при Е; этот угол все время растет в зависимости от все большего удаления наблюдаемой звезды от эклиптики, так что в конце концов наибольшее
изменение проявится в той звезде, которая будет помещаться на самом полюсе эклиптики. Для полного понимания мы Можем доказать это так. Пусть AB будет диаметр земной орбиты, a G ее центр; представим себе диаметр продолженным до звездной сферы в точках D и С и пусть из центра G проведена перпендикулярно плоскости эклиптики ось GF, продолженная до той же сферы; предположим, что на ней же расположен меридиан DFC, перпендикулярный к плоскости эклиптики; взяв на дуге FC любые точки ff и Е, как места неподвижных звезд, проводим
478
ДИАЛОГ О ДВУХ ГЛАВНЕЙШИХ СИСТЕМАХ МИРА
Земля приближается к неподвижным звездам эклиптики и удаляется от них на расстояние диаметра большой орбиты.
линии FA, FB, АН, HG, ИВ, АЕ, GE и BE. Таким образом, углом различия высот или, скажем, параллаксом звезды, находящейся на полюсе F, будет AFB, параллаксом звезды, находящейся в Н, будет угол АЙВ и параллаксом звезды в E будет угол АЕВ. Я утверждаю, что угол различия высот полярной звезды F будет самым большим и что другие углы, наиболее близкие к самому большому, будут больше, чем более удаленные, т. е. что угол F будет больше угла И, а угол H больше угла Е. Предположим, что вокруг треугольника FAB описан круг; так как угол F острый (ибо его основание AB меньше диаметра DC полукруга DFC), то он будет лежать в большем отрезке описанного круга, отсеченном основанием AB, и так как это основание AB разделено в середине под прямыми углами линией FG, то центр описанного круга будет лежать на линии FG; пусть это будет точка 1. Далее, так как из всех линий, проведенных из точки G, не являющейся центром окружности описанного круга, до этой последней, самая большая — та, которая проходит через центр, то FG будет больше всякой другой линии, которая из точки G проводится до окружности этого круга; поэтому такая окружность пересечет линию GH (равную линии GF) и, пересекая GH, пересечет также АН, допустим, в L; проведя линию LB, получим два угла AFB и ALB, равные между собой, так как они опираются на одну и ту же часть описанного круга, но ALB — внешний угол, он больше внутреннего угла H и, следовательно, угол F больше угла Н. Таким же способом мы докажем, что угол H больше угла Е, так как центр круга, описанного около треугольника АН В, лежит на перпендикуляре GF, к которому линия GH ближе, чем линия GE, и потому окружность его пересекает GE, а также АЕ; значит, положение доказано. Итак, мы приходим к заключению, что различие видимого положения
(которое, применяя техническую терминологию, мы можем назвать параллаксом неподвижных звезд) бывает больше или меньше в зависимости от того, находятся ли наблюдаемые звезды более или менее близко к полюсу эклиптики, так что в конце концов у звезд, находящихся на самой эклиптике, это различие сводится к нулю. Далее, что касается приближения Земли к звездам или удаления от них в результате ее движения то по отношению к тем из них, которые находятся на эклиптике, она приближается и удаляется на величину все-
ДЕНЬ ТРЕТИЙ
479
изменения
более
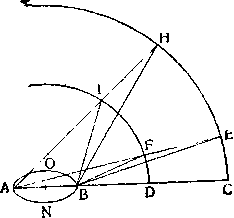
го диаметра земной орбиты, как мы это только что видели; если звезды расположены вблизи полюса эклиптики, то это приближение и удаление почти равны нулю; по отношению же к другим это различие становится тем большим, чем они ближе к эклиптике. В-третьих, мы можем понять, что это видимое изменение становится больше или меньше в зависимости от боль-щей или меньшей близости от нас наблюдаемой звезды; если мы нанесем еще один меридиан в меньшем расстоянии от Земли, каковым пусть будет DFI, то звезда, находящаяся в F ', будет видна в том же направлении АРЕ, если Земля находится в А; если же потом Большие
/пс um. r 7 происходят
наблюдение производить с Земли, находящейся в Б, то звезда близкими звездми, будет видна по лучу BF и угол различия высот BFA будет больше чемсболеедалекими-первого АЕВ, так как он внешний в треугольнике BFE.
Сагредо. С большим удовольствием, а также и пользой слушал я ваши рассуждения и, чтобы убедиться, хорошо ли я все это понял, суммирую заключение в кратких словах. Вы разъяс- обзор явлений, на-
г блюдаемых у непод-
нили нам, как мне кажется, что существуют два вида различных вижных звезд, по-
рождаемых годовым движением Земли.
явлений, происходящих с неподвижными звездами и доступных
нашему наблюдению, причиной которых является возможное годо-
вое движение Земли: первое — это изменение их видимых величин
поскольку мы, переносимые Землею, к ним приближаемся или
от них удаляемся; второе (зависящее от того же удаления или
приближения) — это то, что они кажутся нам на одном и том же
меридиане то более, то менее высокими. Кроме того, вы нам гово-
рите (и я прекрасно это понимаю), что как первое, так и второе из
этих изменений происходит не одинаково со всеми звездами, но с
одной больше, с другой меньше, с третьей же его вовсе не проис-
ходит. Приближение и удаление, в результате которых одна и та
же звезда должна казаться то большей, то меньшей, неощутимо и
почти равно нулю для звезд, близких к полюсу эклиптики, осо-
бенно велико для звезд, находящихся на эклиптике, и имеет сред-
нее значение для промежуточных; противоположное этому на-
блюдается в отношении другого изменения: различие в повышении и
понижении равно нулю у звезд, находящихся на эклиптике, особен-
но велико у звезд, окружающих полюс эклиптики, и имеет
среднее значение у промежуточных. Кроме того, оба эти различия
более заметны у более близких звезд, менее ощутимы у более
удаленных и, наконец, у крайне удаленных должны совершенно
исчезнуть. Вот и все, что касается меня; остается теперь, насколь-
ко я понимаю, удовлетворить синьора Симпличио; не думаю, чтобы
он так легко согласился считать чем-то неощутимым эти различия,
происходящие от столь стройного движения Земли и от такого
480 ДИАЛОГ О ДВУХ ГЛАВНЕЙШИХ СИСТЕМАХ МИРА
изменения, которое переносит Землю в места, отстоящие друг от друга на два таких расстояния, как от нас до Солнца.
Симпличио. Действительно, я, откровенно говоря, очень затрудняюсь признать расстояния до неподвижных звезд столь огромными, чтобы такие разобранные вами различия стали совершенно неуловимыми.
Сальвиати. Не отчаивайтесь, синьор Симпличио, может быть, найдется еще какое-нибудь средство разрешить ваши затруднения. Во-первых, вам вовсе не должно казаться невероятным, что видимая величина звезд ощутимо не изменяется, ибо вы може-приближение и уда- те видеть, что при оценке подобных явлений люди чрезвычайно оитямжся дпредме- сильно обманываются, в особенности наблюдая блестящие пред-шов неуловимы. меты; если вы сами будете смотреть, например, на зажженный факел с расстояния в 200 шагов и если затем он приблизится к вам на 3 или 4 локтя, то неужели вы думаете, что заметите это приближение, потому что он будет казаться вам большим? Я, во всяком случае, его не замечу, даже если он приблизится ко мне на 20 или 30 локтей; мне случалось иногда видеть свет на подобном удалении, и я не мог решить, приближается ли он ко мне или же удаляется от меня, тогда как на самом деле он двигался по направлению ко мне. Да что! Если такое приближение и удаление (я говорю о двойном расстоянии от Солнца до нас) у звезды Сатурна почти совершенно неуловимы, а у Юпитера едва доступны наблюдению, то какими они должны были бы быть в отношении неподвижных звезд, расстояние до которых, я полагаю, вы согласитесь принять не превышающим двойного расстояния до Сатурна. Марс для приближения к нам...
Симпличио. Не затрудняйте себя больше этой частностью, синьор; я уже вполне хорошо понял все то, что было сказано о неизменности видимых величин неподвижных звезд. Но что скажем мы о другой трудности, проистекающей от того, что мы не замечаем никакого изменения в их взаимном расположении? Сальвиати. Скажем кое-что, что, быть может, сможет вас успокоить также и с этой стороны. Короче говоря, не будете ли вы удовлетворены, если на самом деле на звездах будут подмечены те изменения, которые, по вашему мнению, должны были бы наблюдаться, если бы годовое движение принадлежало Земле? Симпличио. Несомненно, буду, поскольку это относится к данной частности.
Сальвиати. Я предпочел бы, чтобы вы сказали так: если это различие заметно, то не остается больше ничего, что могло
ДЕНЬ ТРЕТИЙ 481
бы подвергнуть сомнению подвижность Земли, раз такое явление б
аметно какое-ни-
Если б
НеЛЬЗЯ объЯСНИТЬ НИКаКИМ ДРУГИМ Соображением. НО еСЛИ ВСе за
ЭТО Даже И Не ПрОЯВЛЯеТСЯ ОЩУТИМО, ТО ЭТИМ СаМЫМ ПОДВИЖНОСТЬ иетотш
Земли не опровергается и отсюда не следует с необходимостью ее д3е?0е •%£ ' (Ю3.
неподвижность; ведь, может быть (как утверждает Коперник), рожать.
огромная удаленность звездной сферы делает недоступными на-
блюдению столь ничтожные проявления; возможно, что они, как
уже было сказано, до сих пор никем даже не разыскивались, а если
и разыскивались, то не так, как нужно, т. е. не с той точностью ко-
торая нужна для столь малых величин; эта точность трудно дости-
жима как из-за недостатков астрономических инструментов, под-
верженных воздействию многих факторов, так и по вине тех, кто
ими пользовался с меньшей тщательностью, чем это было необхо-
димо. БезуСЛОВНО убеДИТеЛЬНЫМ ДОКазаТеЛЬСТВОМ ТОГО, Как МаЛО Доказательство то-
можно полагаться на такие наблюдения, служат те различия, ко- пол£гтпься°па0а™?-торые мы находим у астрономов в определении мест — не говорю рономические инст-
уже НОВЫХ ЗВеЗД ИЛИ КОМеТ, НО И СаМЫХ НеПОДВИЖНЫХ ЗВеЗД, И них наблюдениях.
даже высот полюса, где между ними многократно обнаруживаются расхождения на много минут. И, по правде говоря, кто может быть уверен в том, что, работая с квадрантом или секстантом, имеющим сторону самое большее в 3 или 4 локтя длиной, он не ошибется при установлении отвеса или диоптра на две или три минуты, которые на дуге инструмента занимают место не больше поперечника просяного зерна? Кроме того, почти совершенно невозможно изготовить и сохранять инструмент абсолютно точным.
Птолемей ВЫСКаЗЫВаеТ Недоверие К арМИЛЛЯрНОМу Инструменту, Недоверие Птолемея
построенному самим Архимедом для определения вступления готоеленноллр-
Солнца на экватор. медом.
Симпличио. Но если инструменты и самые наблюдения так сомнительны, то как можем мы в конце концов получить до-
стоверные ЗНаНИЯ И ОСВобоДИТЬСЯ ОТ Ошибок? Я СЛЫШаЛ, Как ОЧеНЬ Инструменты Тихо
_ m сделаны с большими
ХВаЛИЛИ ИНСТрумеНТЫ 1ИХО, Сделанные С ОГрОМНЫМИ Затратами, затратами.
и его необыкновенную тщательность в наблюдениях 47.
Сальвиати. Все это я допускаю, но ни первого, ни второго недостаточно, чтобы мы могли быть уверены в столь важном вопросе. Я хочу чтобы мы пользовались инструментами, значи-тельно превосходящими по величине инструменты Тихо, чрезвычайно точными и. сделанными с очень малыми затратами, со стороною в 16, 20, 30 и 50 миль, так что градус имеет ширину в милю, минута — в пятьдесят локтей и секунда — немногим меньше локтя; и мы можем получить такие инструменты любой величины без всяких расходов 48. В бытность мою на одной из моих вилл поблизости от Флоренции я совершенно отчетливо наблюдал, как
3' Галилео Галилей, т. I
482
хожденияыхож- Солнце вступило в летнее солнцестояние, а затем вышло из него, делил Солнца при когда однажды вечером при своем заходе оно скрылось за одной из
летнем солнцестоя- тт « г>
нии. скал гор Ньетрапана, удаленной примерно на Ь миль, оставив от
себя тонкую полоску, направленную к северу, ширина которой не составляла и сотой части диаметра Солнца; на следующий вечер при подобных же обстоятельствах Солнце показало также соответствующую частицу, но заметно более тонкую, очевидное доказательство того, что оно начало удаляться от тропика; отступление Солнца за время от первого до второго наблюдения, конечно, не составляло на горизонте и одной секунды; однако наблюдение — оно производилось потом с помощью точного телескопа, который увеличивает диск Солнца более чем в тысячу раз, — удается легко и вместе с тем доставляет удовольствие. Вот я и хочу, чтобы посредством подобных инструментов мы производили наши наблюдения над неподвижными звездами, пользуясь какой-нибудь из тех звезд, в которых изменения должны быть особенно значительными; таковы, как было уже разъяснено, наиболее удаленные от эклиптики; из них Вега — громаднейшая звезда в созвездии Лиры, близкая к полюсу эклиптики, — очень удобна в странах достаточно северных, если действовать так, как я сейчас скажу,
Место, подходящее НО Сам Я ПОЛЬЗОВаЛСЯ ПрИ ЭТОМ ДруГОЙ ЗВ63ДОЙ. Я уже ПОДМ6-
подви£шх1зд,по- тил и место, вполне приспособленное для таких наблюдений. Мес-скольки это касает- то Это — открытая равнина; на ней поднимается с севера очень вы-
ся годового движе- „
кия земли. сокая гора, на вершине которой построена маленькая церковка,
расположенная с запада на восток, так что конек ее кровли может пересекать под прямым углом меридиан жилища, находящегося на равнине. Я хочу установить брусок, параллельный этому коньку крыши и отстоящий от него примерно на один локоть; установив его, я буду искать по равнине такое место, с которого одна из звезд Большой Медведицы при прохождении через меридиан скрывалась бы за укрепленный брусок; если же он окажется недостаточно толстым, чтобы заслонить всю звезду, я найду такое место, откуда будет видно, как тот же самый брусок пересекает по середине диск этой звезды — явление, которое посредством хорошего телескопа различается отлично; если в том месте, откуда можно наблюдать это явление, имеется какое-нибудь жилище, то это будет тем удобнее; если же нет, то я прикажу вкопать в землю достаточно прочно столб с постоянной отметкой для указания того места, где надо помещать глаз каждый раз, когда пожелают возобновить наблюдение; первое из этих наблюдений я произведу во время поворота на летнее солнцестояние и буду продолжать его потом ежемесячно или когда мне захочется, вплоть до
ДЕНЬ ТРЕТИЙ 483
другого поворота на солнцестояние; посредством этого наблюдения можно будет обнаружить повышение или понижение звезды, каким бы малым оно ни было. И если при таком наблюдении удастся воспринять какое-нибудь изменение, то какая польза будет от этого астрономам! Ведь этим самым мы не только удостоверимся в годовом движении, но сможем подойти также и к познанию величины и удаленности этой звезды.
Сагредо. Я очень хорошо понимаю весь этот замысел, и вся эта операция кажется мне столь легкой и приспособленной для надлежащей цели, что с большим основанием можно предположить, что сам Коперник или другие астрономы применяли этот способ.
Сальвиати. Ая думаю совершенно обратное, так как мало вероятно, чтобы кто-нибудь его испытал и не упомянул о результатах, безразлично, говорят ли они в пользу того или другого мнения; кроме того, ни для этой, ни для какой другой цели никто не прибегал к такому способу наблюдения, потому что без точного телескопа оно даже не может быть как следует осуществлено.
Сагредо. Я совершенно успокоен вашими словами. Но так как нам остается еще много времени до ночи, то, если вы хотите, чтобы я провел ее спокойно, возьмите на себя труд объяснить нам те проблемы, разъяснение которых вы раньше просили отсрочить до завтра; верните добровольно данное нами согласие, и, оставив в стороне все другие соображения, объясните нам, как из признания тех движений, которые Коперник приписывает Земле, и предположения о неподвижности Солнца и о неподвижных звездах могут вытекать те же самые явления в отношении повышения и понижения Солнца, изменения времен года, неравенства дней и ночей и т. д., которые так просто и легко объясняются системой Птолемея.
Сальвиати. Не следует и даже невозможно пренебрегать тем, что интересует синьора Сагредо. И отсрочка, о которой я просил, нужна была только для того, чтобы выиграть время и привести в порядок в памяти те предпосылки, которые служат для широкого и ясного объяснения того, как названные явления вытекают и из системы Коперника так же, как и из системы Птолемея, причем из первой даже с гораздо большей легкостью и простотой, чем из второй, откуда с очевидностью следует, что первая гипотеза система коперни-
НаСТОЛЬКО Же ЛеГКО МОЖеТ ОСущеСТВЛЯТЬСЯ В Природе, НаСКОЛЬКО ка представляет
J v „ х г трудности для по-
трудно воспринимается разумом. Все же я надеюсь, что, применяя нгшшшя, но не для другой способ объяснения, отличный от объяснения Коперника, осуществления. я смогу сделать его положения значительно менее темными; ради
31*
484
Предпосылки, необходимые для того, чтобы, правильно понять следствия, вытекающие из движения Земли.
Чрезвычайно простой чертеж:, представляющий систему Коперника и се следствия.
этого я установлю несколько предпосылок, которые сами по себе известны и очевидны. Они таковы.
Первая. Если принять, что Земля — сферическое тело — вращается вокруг собственной оси и полюсов, то каждая точка, отмеченная на ее поверхности, описывает окружность круга, большего или меньшего, в зависимости от того, находится ли она более или менее далеко от полюсов; наибольший из этих кругов — тот, который очерчивается точкой, равно удаленной от полюсов; все такие круги параллельны друг другу; мы их будем называть параллелями.
Вторая. Если Земля имеет сферическую форму и состоит из непрозрачного вещества, то одна половина ее поверхности непрерывно освещается Солнцем, в то время как другая половина остается темной; и так как граница, разделяющая освещенную часть от темной, является большим кругом, то мы будем называть его пограничным кругом света.
Третья. Когда пограничный круг света пройдет через полюсы Земли, то он рассечет (раз он большой круг) все параллели на равные части; если же он проходит не через полюсы, то он рассекает параллели на неравные части, за исключением одного только среднего круга, который, являясь большим, снова будет рассечен на равные части.
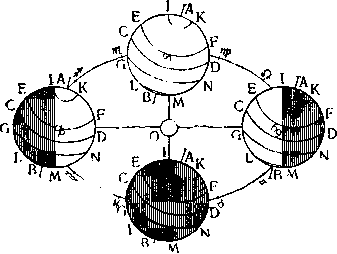
Четвертая. Если Земля вращается вокруг собственных полюсов, то величина дней и ночей определяется дугами параллелей, пересеченных пограничным кругом света; дуга, которая приходится на освещенную полусферу, определяет длину дня, а остающаяся — величину ночи.
Предположив все это, для более ясного понимания того, что будет сказано далее, сделаем такой чертеж: во-первых, наметим окружность круга, который представит нам земную орбиту, описанную в плоскости эклиптики, и разделим ее на четыре равные части двумя
диаметрами, Козерог — Рак и Весы — Овен, которые в то же время представят нам четыре главные точки, т. е. два солнцестояния и два равноденствия; в середине этого круга наметим
ДЕНЬ ТРЕТИЙ 485
Солнце О, устойчивое и неподвижное. Наметим теперь вокруг четырех точек — Козерога, Рака, Весов и Овна — как центров четыре равных круга, которые будут нам представлять Землю, находящуюся в них в разные времена; на протяжении одного года
