№
|
Учебный элемент / Текст вопроса
|
Количество ответов
|
Процент правильных ответов
|
1
|
Среднее арифметическое. Знание понятия среднего арифметического ряда чисел.
|
Среднее арифметическое ряда чисел 1, 3, 4, 6, 8, х, 14 равно 7. Определите неизвестное число х.
А) 12;
|
Б) 9;
|
В) 11;
|
Г)10;
|
Д)13.
|
|
|
7878
|
75%
|
2
|
Числовые промежутки. Знание определения отрезка.
|
Сумма всех целых чисел отрезка от –202 до 205 равна
А) 612;
|
Б) 407;
|
В) 609;
|
Г) 412;
|
Д) 607.
|
|
|
7865
|
26%
|
3
|
Комбинаторика. Знание определения перебора элементов.
|
Перед нами 6 закрытых замков и 6 ключей к ним. К каждому замку подходит только один ключ, но ключи смешались. Возьмем один из замков и попробуем открыть его каждым из 6 ключей. В лучшем случае мы откроем первым же ключом, в худшем - только последним.
Сколько нужно в худшем случае произвести проб, чтобы ко всем замкам подобрать ключи?
А) 21;
|
Б) 20;
|
В) 36;
|
Г) 15;
|
Д) 12.
|
|
|
7901
|
6%
|
4
|
Комбинаторика. Знание понятия сочетания элементов.
|
В магазине "Чайная церемония» есть 7 разных чашек и 4 разных блюдца. Сколькими способами можно купить чашку с блюдцем?
А) 56;
|
Б) 28;
|
В) 7;
|
Г) 14;
|
Д) 4.
|
|
|
7895
|
74%
|
5
|
Линейная функция. Знание свойств линейной функции.
|
Сумма координат точки пересечения функций y=2x - 3 и y=5x+21 равна
А) 15;
|
Б) –11;
|
В) –27;
|
Г) 23;
|
Д) 27.
|
|
|
7506
|
51%
|
6
|
Функция. Знание нахождения значений функции.
|
Для функции y=x(x+2), 0 ≤ х ≤ 4, укажите те числа, которые являются ее значениями.
А) –1;
|
Б) 3;
|
В) 26;
|
Г) 8;
|
Д) 24;
|
Е) 35.
|
|
|
7522
|
64%
|
7
|
Биография ученого, в честь которого проводится олимпиада. Знание биографии Окунькова А.
|
Первые работы А.Ю. Окунькова относились к:
А) теории представлений;
Б) теории физических явлений;
В) теории функции комплексной переменной;
Г) теории случайных матриц;
Д) теории струн;
Е) теории форм поверхностей кристаллов.
|
|
7435
|
62%
|
8
|
Уравнения с одной переменной. Знание алгоритма решения уравнений с одной переменной.
|
Выберите из предложенных уравнений те, которые имеют корень, равный –2.
А) 5,3x - 13 = 1,8x + 32;
Б) -12,5 + 3x = -1,5 - 3x;
В) 12 - 0,8x = 26 + 6,2x;
Г) 0,25x = - 0,05;
Д) 1,5x + 4,5 = 2x + 5,5;
У) -0,05x - 0,75 = - 0,5x - 1,65.
|
|
7650
|
66%
|
9
|
Статистические характеристики. Знание определений основных статистических характеристик.
|
Укажите среднее арифметическое, размах и медиану ряда чисел 16, 12, 10, 6, 18, 8, 14, 20.
А) 13
|
Б) 14
|
В) 16
|
Г) 8
|
Д) –3
|
Е) 12
|
|
|
7582
|
68%
|
10
|
Числовые выражения. Знание понятия делителя числа.
|
Укажите все простые делители суммы 2 + 22 + 23 + 24.
А) 1;
|
Б) 5;
|
В) 3;
|
Г) 2;
|
Д) 7;
|
Е) 11.
|
|
|
7667
|
74%
|
11
|
Обыкновенные дроби. Знание соответствия дробей и частей круга.
|
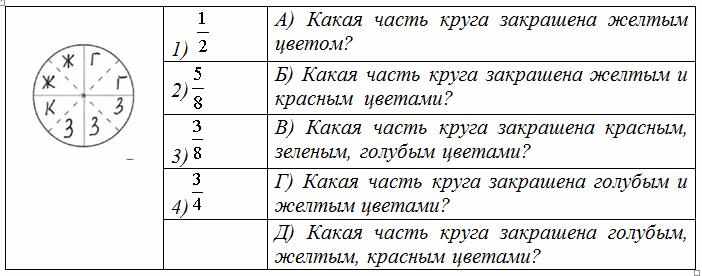
Установите соответствие между выражением и словесной формулировкой.

|
|
7979
|
84%
|
12
|
Основные геометрические понятия. Знание основных определений курса геометрии
|
Установите соответствие между дробью и предложением.
|
|
7978
|
81%
|
13
|
Основные геометрические свойства и теоремы. Знание геометрических свойств и теорем.
|
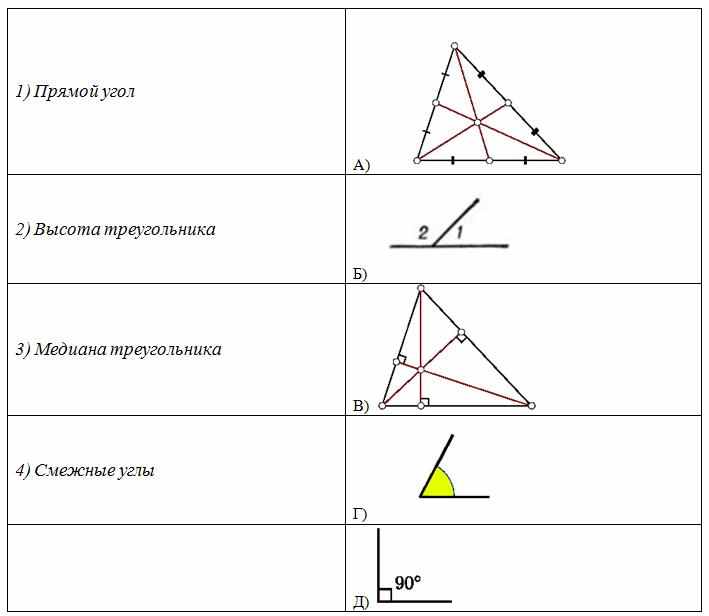
Установите соответствие между понятиями и рисунками.
|
|
7979
|
84%
|
14
|
Основные геометрические свойства и теоремы. Знание геометрических свойств и теорем.
|
Установите соответствие между понятием и свойством, определяющим это понятие.
1) Смежные углы
|
А) Углы при основании равны;
|
2) Равнобедренный треугольник
|
Б) Его длина равна двум радиусам;
|
3) Диаметр
|
В) Сумма односторонних углов равна 180º;
|
4) Параллельные прямые и секущая
|
Г) Они равны;
|
|
Д) Их сумма равна 180º.
|
|
|
7979
|
63%
|
15
|
Сложение и вычитание многочленов. Знание правил сложения и вычитания многочленов.
|
Установите соответствие между равенством (левый столбец) и значением К (правый столбец), при котором равенство обращается в тождество.
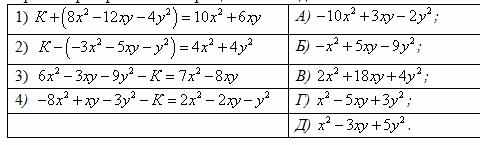
|
|
7979
|
51%
|
16
|
Степень с натуральным показателем. Знание свойств степени с натуральным показателем.
|
Расположите числа в порядке убывания.
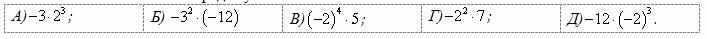
Варианты ответов расставте в нужной последовательности, удерживая левой кнопкой мыши.
|
|
7979
|
20%
|
17
|
Линейная функция. Знание определения линейной функции.
|
Определите функции, являющиеся линейными.
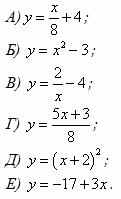
|
|
7327
|
65%
|
18
|
Степень с натуральным показателем. Знание определения степени с натуральным показателем.
|
Укажите числа, являющиеся квадратами или кубами известных Вам чисел.
А) 2,5;
|
Б) 0,000008;
|
В) 2,89;
|
Г) 14,4;
|
Д) 0,216;
|
Е) 22,5.
|
|
|
7161
|
57%
|
19
|
Степень с натуральным показателем. Знание свойств степени с натуральным показателем.
|
Расположите в порядке возрастания числа х, х2, х3, х4, если –1 < х < 0.
А) х < х2 < х3 < х4;
|
Б) х3 < х < х2 < х4;
|
В) х < х3 < х2 < х4;
|
Г) х < х3 < х4 < х2;
|
Д) х3 < х < х4 < х2.
|
|
|
|
7220
|
24%
|
20
|
Линейная функция. Знание нахождения значения функции.
|
Линейная функция задана формулой у = –2х + 1. Укажите точки, принадлежащие графику этой функции.
А) (–2; 4);
|
Б) (7; –13);
|
В) (–3; 7);
|
Г) (–5; 10);
|
Д) (–0,5; 2).
|
|
|
7139
|
68%
|
21
|
Натуральные числа. Знание основ решения задач на логику.
|
В классе 27 учеников, из них 16 посещают театральный кружок , 11- увлечены математикой, 8 ребят не посещают эти кружки. Сколько математиков увлечены театром? В ответ запишите только число.
|
|
7979
|
51%
|
22
|
Проценты. Знание понятия процента.
|
На элеватор привезли 1600 т пшеницы двух сортов. После обработки пшеницы первого сорта отходы составили 2%, второго сорта – 4%. Всего получилось 1558 т чистой пшеницы. Сколько пшеницы первого и второго сортов отдельно привезли на элеватор? В ответ запишите только числа (сначала первого сорта, потом второго) разделяя их запятой без пробелов.
|
|
7979
|
17%
|
23
|
Математические термины. Знание основ решения задач на логику.
|
Абсцисса, интервал, миллиард, ордината, геометрия, пирамида, логарифм. Какое слово здесь лишнее? Ответ запишите с маленькой буквы в именительном падеже.
|
|
7979
|
18%
|
24
|
Свойства равнобедренного треугольника. Знание свойства высоты равнобедренного треугольника, проведенной к основанию.
|
Игровая площадка имеет форму квадрата АВСD, диагонали его пересекаются в точке О. Незнайка, гуляя по площадке, сосчитал, что периметр треугольника АВD равен 102 м, а периметр треугольника АВО равен 62 м. Помогите Незнайке сосчитать, сколько метров составляет расстояние от точки А до точки О? В ответ запишите только число.
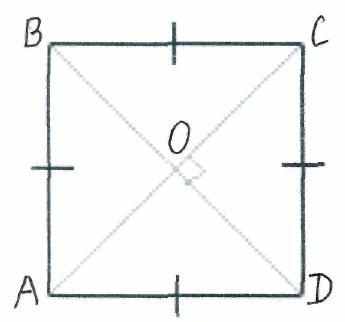
|
|
7979
|
23%
|
25
|
Масштаб. Знание перевода величин из одной единицы измерения в другую, знание определения масштаба.
|
Готовясь к походу, семиклассники решили воспользоваться картой, масштаб которой 1 : 1000000. Помогите ребятам узнать, сколько понадобится им времени, чтобы проехать на велосипедах со скоростью 10 км/ч до первого привала, если расстояние на карте от пункта отправки до привала равно 0,5 дм. В ответ запишите только число.
|
|
7979
|
56%
|
№
|
Учебный элемент / Текст вопроса
|
Количество ответов
|
Процент правильных ответов
|
1
|
Площадь круга. Знание формулы площади круга, понятия отношения.
|
Отношение площадей двух кругов равно 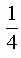 , а радиус большего круга равен 4 см. Тогда радиус меньшего круга равен , а радиус большего круга равен 4 см. Тогда радиус меньшего круга равен
А) 2π см;
|
Б) 0,5 см;
|
В) 4 см;
|
Г) 2 см;
|
Д) 1 см.
|
|
|
6490
|
40%
|
2
|
Двойное неравенство. Знание основных свойств решения неравенства.
|
Найдите сумму всех целых значений х, удовлетворяющих неравенству -18 ≤ -3х < -3.
А) 20;
|
Б) 21;
|
В) 14;
|
Г) -21;
|
Д)-20.
|
|
|
6448
|
52%
|
3
|
Степень с целым показателем. Знание свойств степени с целым показателем.
|
Выполните указанные действия: (7,8 ∙ 108) ∙ (8,7 ∙ 10–3).
А) 678,6 ∙ 105;
|
Б) 6,786 ∙ 105;
|
В)0,6786 ∙ 106;
|
Г)67,86 ∙106;
|
Д) 6,786 ∙ 106.
|
|
|
6475
|
50%
|
4
|
Квадратные уравнения. Знание теоремы Виета и теоремы, обратной теореме Виета.
|
Найдите сумму корней уравнения: 4x2 - x - 12 = 0.
А) –0,25;
|
Б) 0,25;
|
В) 12;
|
Г) 1;
|
Д) –1.
|
|
|
6307
|
49%
|
5
|
Уравнения. Знание теоремы Виета и теоремы, обратной теореме Виета. Знание свойств произведения двух выражений.
|
Найдите произведение корней уравнения: (3x + 1)(2x2 + x - 3) = 0.
А) –0,5;
|
Б) 5;
|
В) 0,5;
|
Г)1;
|
Д) –1.
|
|
|
6313
|
45%
|
6
|
Квадратичная функция. Знание вида графиков квадратичной функции.
|
Выясните, график какой функции изображен на рисунке.
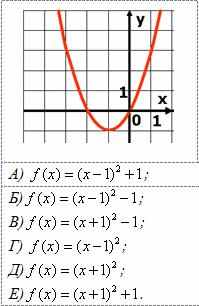
|
|
6357
|
51%
|
7
|
Квадратичная функция. Знание понятия оси симметрии параболы.
|
Найдите на оси Ох точку, через которую проходит ось симметрии параболы 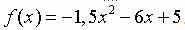 . .
А) (–2;0);
|
Б) (2;0);
|
В) (–4;0);
|
Г) (4;0);
|
Д) (–8;0);
|
Е) (8;0).
|
|
|
6148
|
41%
|
8
|
Биография ученого, в честь которого проводится олимпиада. Знание биографии Окунькова А.
|
Первые работы А.Ю. Окунькова относились к
А) теории представлений;
|
Б) теории физических явлений;
|
В) теории функции комплексной переменной;
|
Г) теории случайных матриц;
|
Д) теории струн;
|
Е) теории форм поверхностей кристаллов.
|
|
|
6222
|
60%
|
9
|
Параллелограмм. Знание свойств параллелограмма.
|
Длины сторон параллелограмма равны 3 см и 8 см. Биссектриса острого угла параллелограмма делит большую сторону слева направо на отрезки, равные
А)7см, 1см;
|
Б) 2 см, 6 см;
|
В) 1 см, 7 см;
|
Г) 4 см, 4 см;
|
Д) 6 см, 2 см;
|
Е) 3 см, 5 см.
|
|
|
6422
|
58%
|
10
|
Действительный числа. Знание основных свойств чисел, знание порядка выполнения действий.
|
Выполнить действия:
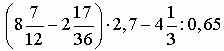

|
|
6355
|
58%
|
11
|
Квадратные уравнения. Знание теоремы Виета и теоремы, обратной теореме Виета, формул сокращенного умножения.
|
Пусть х1, х2 – корни приведенного квадратного уравнения x2 + px + q = 0.
Установите соответствие между левой и правой частями таблицы.
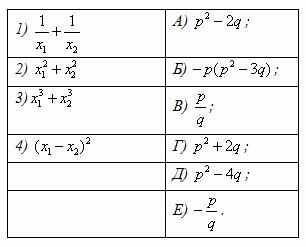
|
|
6599
|
35%
|
12
|
Площадь. Знание формул вычисления площадей треугольника, трапеции, прямоугольника, параллелограмма.
|
Установите соответствие между условием задачи и значением площади фигуры.
1) Периметр прямоугольника равен 80 см, а отношение сторон равно 2 : 3.
|
А) 7 см2;
|
2) Две стороны параллелограмма равны 6 см и 8 см, а один из углов равен 150о.
|
Б) 384 см2;
|
3) Две стороны треугольника равны 12 см и 9 см, а угол между ними 30о.
|
В) 27 см2;
|
4) Острый угол равнобедренной трапеции равен 45о, а основания равны 8 см и 6 см.
|
Г) 24 см2;
|
|
Д) 54 см2;
|
|
Е) 48 см2.
|
|
|
6599
|
47%
|
13
|
Квадратные уравнения. Знание условия существования корней.
|
Установите соответствие между условием и уравнением. 
|
|
6599
|
45%
|
14
|
Площадь. Знание формул вычисления площадей прямоугольного треугольника, трапеции, прямоугольника, параллелограмма.
|
Установите соответствие между геометрической фигурой и верной формулировкой нахождения ее площади.
1) прямоугольник
|
А) площадь равна произведению двух его сторон;
|
2) параллелограмм
|
Б) площадь равна половине произведения его катетов;
|
3) прямоугольный треугольник
|
В) площадь равна половине произведения его стороны на какую-либо высоту;
|
4) трапеция
|
Г) площадь равна произведению стороны на высоту, проведенную к этой стороне;
|
|
Д) площадь равна половине произведения суммы оснований на высоту;
|
|
Е) площадь равна произведению двух его смежных сторон.
|
|
|
6599
|
53%
|
15
|
Числовые выражения. Знание метода выделения полного квадрата, свойства квадратного корня.
|
Установите соответствие между выражением и его значением.

|
|
6599
|
34%
|
16
|
Степень с целым показателем. Знание свойств степени с целым показателем.
|
Расположите числа в порядке возрастания.
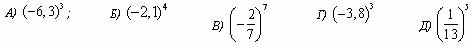
Варианты ответов расположите в нужном порядке, удерживая левой кнопкой мыши.
|
|
6599
|
48%
|
17
|
Квадратные уравнения. Знание определения количества корней квадратного уравнения в зависимости от знака дискриминанта.
|
Укажите квадратные уравнения, имеющие два корня.
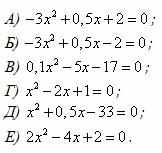
|
|
5855
|
60%
|
18
|
и ее график. Знание вида графика линейной функции.
|
Укажите прямые, которые пересекают график функции
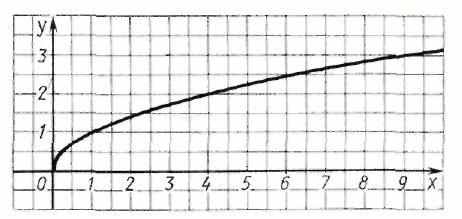
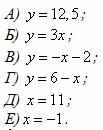
|
|
6010
|
58%
|
19
|
Степень с натуральным показателем. Знание свойств степени с натуральным показателем.
|
Расположите в порядке возрастания числа х, х2, х3, х4, если -1 < х < 0.
А) х < х2 < х3 < х4;
|
Б) х3 < х < х2 < х4;
|
В) х < х3 < х2 < х4;
|
Г) х < х3 < х4 < х2;
|
Д) х3 < х < х4 < х2.
|
|
|
|
6022
|
27%
|
20
|
Действительные числа. Знание определения иррациональных чисел.
|
Среди данных чисел укажите те, которые являются иррациональными.
А) 0,(23);
|
Б) 0,212112111…;
|
В) 1,25;
|
Г) π ;
|
Д) 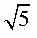 ; ;
|
Е) -6,7;
|
|
|
6142
|
67%
|
21
|
Натуральные числа. Знание понятия квадрата числа и основ решения задач на логику.
|
Имеется два ряда чисел. Какое число должно стоять вместо вопросительного знака?
12; 13; 14; 15; 16
441; 961; 691; ? 652
|
|
6599
|
34%
|
22
|
Преобразование рациональных выражений. Знание понятия среднего гармонического ряда чисел.
|
Грузовик первую половину пути из города А в город В прошел со скоростью 50 км/ч, а вторую половину пути – со скоростью 25 км/ч. Из города В вгород А грузовик шел со скоростью 50 км/ч. Найдите среднюю скорость автомобиля на всем пути. В ответ запишите только число.
|
|
6599
|
17%
|
23
|
Нахождение расстояния до недоступной точки. Знание признаков подобия треугольников.
|
Найдите расстояние от точки А до недоступной точки В, если АС = 150 м, DF||АВ, DF = 16 м, CD = 30 м. В ответ запишите только число.
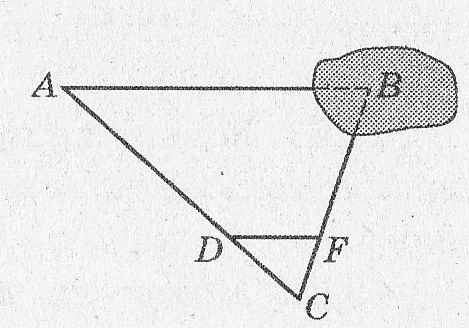
|
|
6599
|
26%
|
24
|
Равнобедренный треугольник. Знание свойств равнобедренного треугольника.
|
Определите величину угла АЕВ, если АВСD – квадрат, треугольник АЕD – равносторонний. В ответ запишите только число.
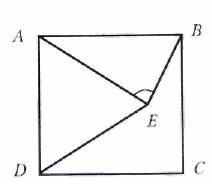
|
|
6599
|
28%
|
25
|
Квадратные уравнения. Знание основ решения задач на перебор вариантов.
|
Участники конференции при ее открытии обменялись рукопожатиями. Корреспондент одной из газет подсчитал, что всех рукопожатий было 78. Сколько было участников конференции? В ответ запишите только число.
|
|
6599
|
33%
|




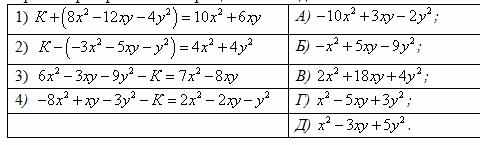
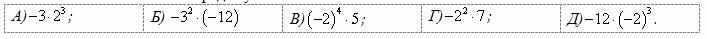
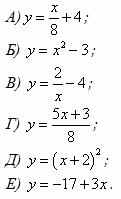

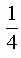 , а радиус большего круга равен 4 см. Тогда радиус меньшего круга равен
, а радиус большего круга равен 4 см. Тогда радиус меньшего круга равен
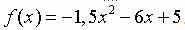 .
. 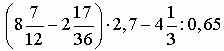

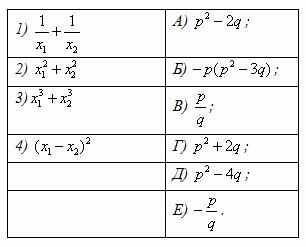


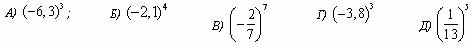
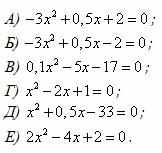

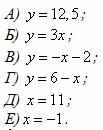
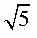 ;
;
