7 класс Уласевич Ольга Николаевна, гимназия №12 г. Липецка

Вид материала

Документы

Содержание Краткая пояснительная записка II. История вопроса. Первое понятие. "Зависимость". Работа с текстом. Т. 2 (стр. 44-45 "Образы Ф.М. Достоевского в иллюстрациях Ильи Глазунова". III. Введение математической модели "функция" Первичное закрепление Функциональная терминология. Вторичное закрепление понятия "функция", функциональной терминологии. Проверка усвоенных понятий . Опорный блок. Закон развития мира

Подобный материал:

• Емельянова Лидия Михайловна, моу гимназия №12 г. Липецка Тема урок, 45.12kb.
• Дидык Ольга Павловна гоу гимназия 45 г. Москва Класс: 6 Тема: Горные породы Количество, 74.25kb.
• Ручкина Галина Викторовна, моу гимназия №1 г. Липецка 9 класс, право Правовое регулирование, 48.15kb.
• Урок русского языка ( 2 класс ) Тема: правописание непроверяемых, 195.36kb.
• Дидык Ольга Павловна гоу гимназия 45 г. Москва Класс: 6 Тема : Гидросфера. Мировой, 72.81kb.
• Урок изобразительное искусство. 7г класс, общеобразовательный. Безрядина Елена Николаевна,, 97.95kb.
• Пономарева Ольга Николаевна Музыка 6 класс Программно-методическое обеспечение: программа, 72.99kb.
• Дидык Ольга Павловна гоу гимназия 45 г. Москва Класс: 6 Тема: Формирование рельефа., 131.29kb.
• М. И. Неделина г. Липецка > Котяева Наталья Николаевна Литературное краеведение, 251.67kb.
• М. И. Неделина г. Липецка > Дятчина Ольга Михайловна Литературное краеведение > 7 класс, 58.36kb.

Алгебра

7 класс

Уласевич Ольга Николаевна, гимназия № 12 г. Липецка

Тема: «Что такое функция?»

Цель:

• повторить основные понятия алгебры (число, уравнение, тождество), вопрос адекватности аналитической и геометрических моделей на примере линейного уравнения;
  

• ввести функциональную терминологию (функция, аргумент, значение функции, область определения функции, область значений функции), способами задания функции;
  
• формирование у учащихся умения находить по формуле, графику значение функции по известному значению аргумента;
  
• усиление прикладной направленности курса алгебры через рассмотрение примеров реальных зависимостей между величинами с опорой на опыт учащихся.
  

Краткая пояснительная записка

Данная тема является начальным этапом в обеспечении систематической функциональной подготовки учащихся. В программе «Алгебра 7» автора А.Г. Мордковича предлагается «употреблять термины «функция», «область определения функции» и др. без знания строгих математических определений этих понятий, на описательном, наглядно-интуитивном уровне до 9 класса.

Считаю необходимым выделить 2 часа на определение и отработку важнейших математических понятий уже в 7 классе (из часов резерва)

1. Актуализация знаний учащихся.
   

Школьная алгебра держится на 4 китах: число, тождество, уравнение и …

Не будем двигаться вперед, пока не убедимся, что на первых трех мы плаваем довольно сносно.


1)


5→ -5 →12 → -1.2 нет →7

-8 → -18 → -1 → +0,1 да → 7

• Какие математические модели помогут нам всегда идти по дороге согласия?
  

1 ^х 1

x ²ⁿ

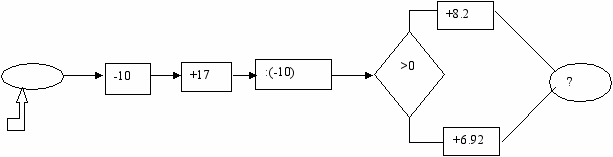
• по какой формуле работает наш аппарат до логического блока?
  

f =(a-10+17) : (-10) = (a+7) : (-10)

• почему только на выходе стоит знак вопроса, а на входе его нет?
  

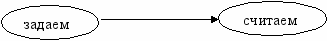f

y=f(x)

x y

2. “Мне приходится делить свое время между политикой и уравнениями. Однако, уравнения гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно.”
   

А. Энштейн

(x³-4x)(x²+6x+9)(3^2x-27)(x²+9)(|x| - 3)( |x| +7) (x²-4x+10)=0

Как изменилось бы решение уравнения, если бы был еще один множитель



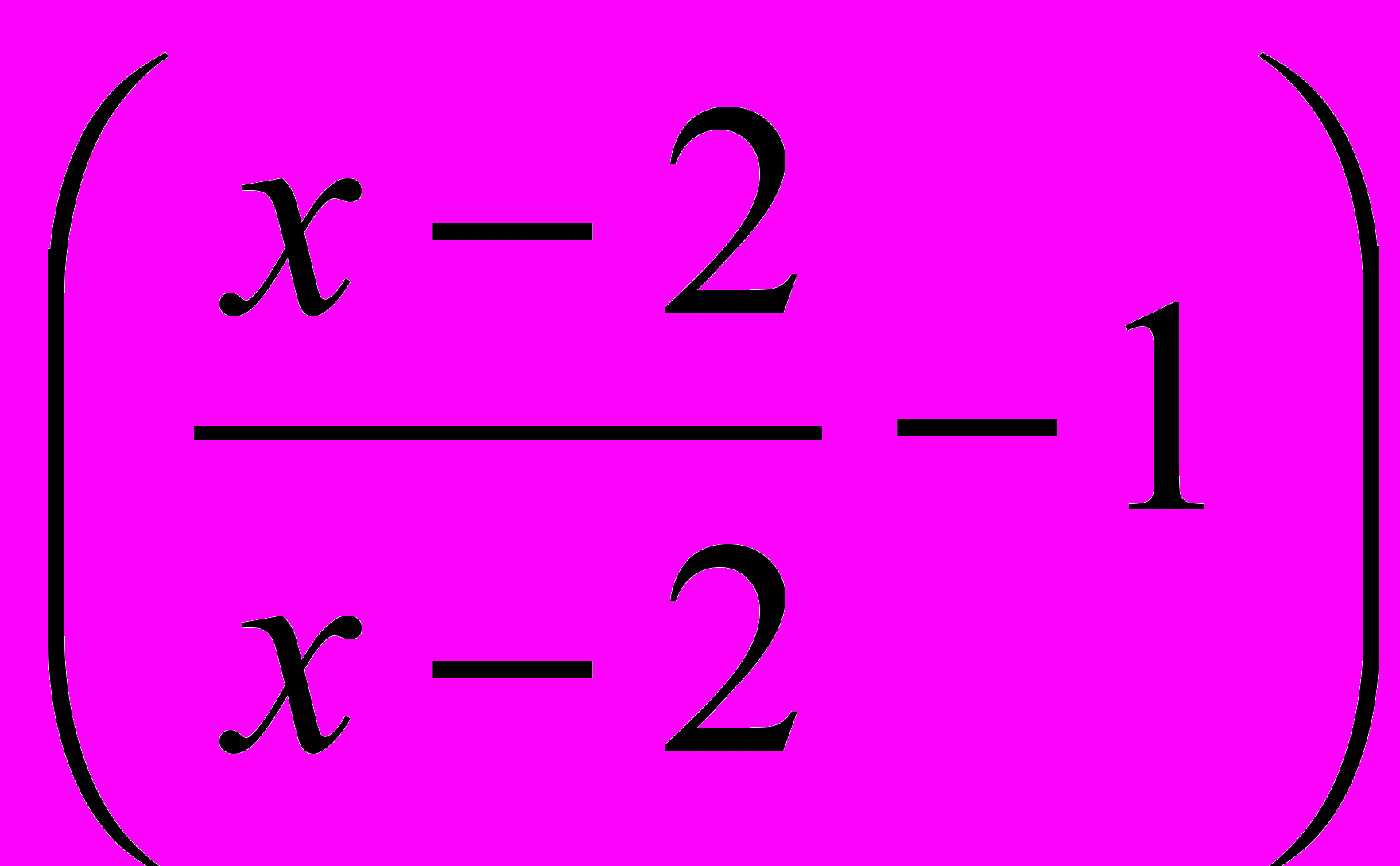
X є R , кроме 2

3) Что является графиком уравнения


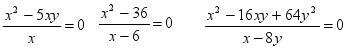0х + 0у +о = 0

0х + 0у + 5 = 0

4

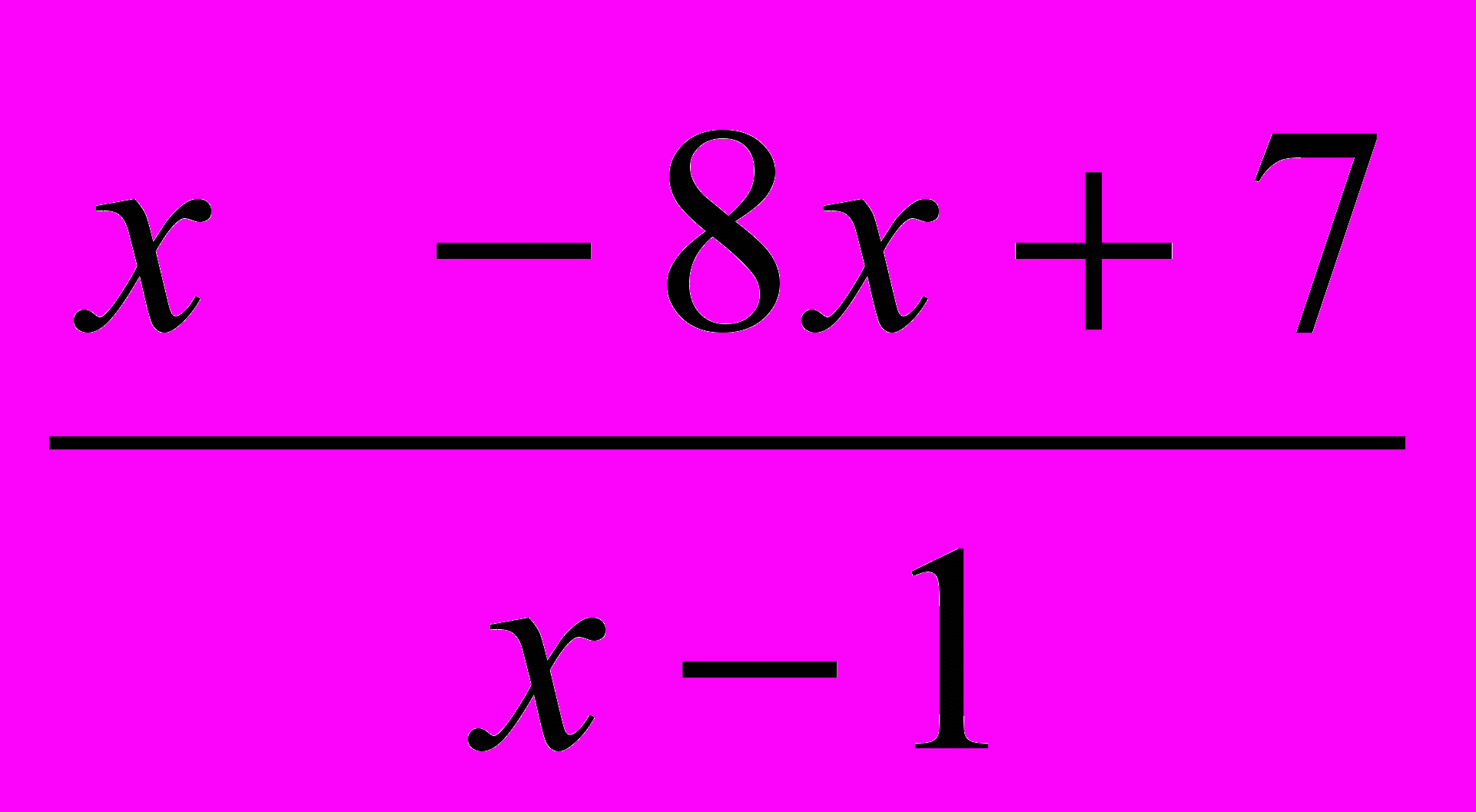
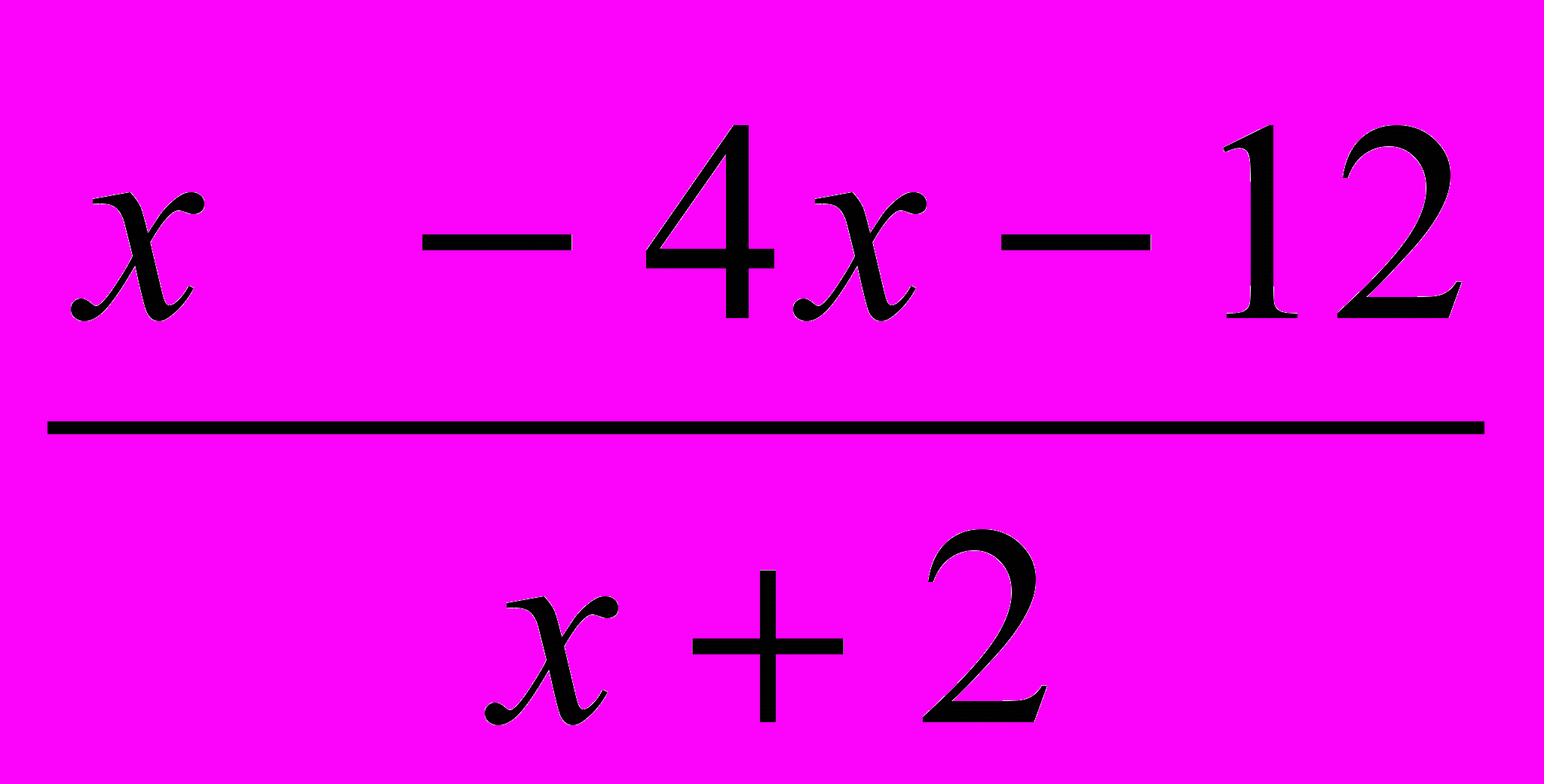
) Сократите алгебраическую дробь


При каких условиях полученные равенства станут тождествами?

II. История вопроса. Первое понятие. "Зависимость".

Пришло время познакомиться с 4 китом - функцией.

В переводе с латинского "funetio" - исполнение, осуществление.

В конце урока нам предстоит ответить на вопрос:

Соответствует ли значение слова математическому определению?

В математике слово "функция" впервые было употреблено в 17 веке немецким ученым Готфридом Лейбницем, но сами функции носами функции и способы их задания изучались очень давно, практически тогда же, как числа и уравнения.

Стараясь узнать новое, мы прежде всего знакомимся с историей вопроса.

Работа с текстом.

Т1. В тексте №1 вам необходимо найти "опорные" слова, понятия от которых мы и оттолкнемся.

идея изменения и движения зависимость одной переменной величины от другой

В философских трактатах одним из важнейших принципов движения и развития мира является признание всеобщей зависимости предметов и явлений.

На прошлом уроке, составляя линейные уравнения с 2 переменными для описания реальных процессов, мы заметили, что не только они могут помочь в моделировании практических ситуаций. На дом было предложено найти примеры зависимостей в различных науках, искусстве и прочее.

И я объявляю

"Аукцион зависимостей"

работа по рядам

наука: неповторяющаяся информация

физика, химия, география, …..

Если идеализировать условия протекания процессов - возникает математическая модель.

Завершаем аукцион математическим приветствием всех его участников.

Физкультминутка: (помогает ученик)

Мы при встрече улыбнемся,

подмигнем слегка друг другу,

Вправо, влево повернемся

И кивнем, затем по кругу

Все идеи победили -

Вверх взметнулись наши руки.

Груз забот с себя стряхнули

И продолжим путь науки.

Действительно, зависимость предметов, явлений наблюдается повсюду.

Посмотрите на картины Константина Васильева "Лесная сказка" и "Лесная готика" и здесь зависимость между названием и содержанием, содержанием и выбранным цветом, цветом и стилем: загадкой сказки и строгостью готических форм.

Художники и писатели часто применяют прием - зависимость внешней и внутренней сторон человека, их описания.

Послушайте отрывок из незаконченного романа Федора Михайловича Достоевского

"Неточка Незванова" и на картине Ильи Глазунова найдите: изображение которой из девушек подходит описание.

Т. 2 (стр. 44-45 "Образы Ф.М. Достоевского в иллюстрациях Ильи Глазунова".

III. Введение математической модели "функция"

знакомство с функциональной терминологией.

Вы уже догадались, что слова " зависимость" и "функция" связаны друг с другом.

Действительно,

функция - это всегда зависимость, но не каждая зависимость будет являться функцией, другими словами:

числовая функция

зависимость

не является числовой функцией

Обратимся к научной литературе.

Т.3 - Найдите определение функции, назовите "основное" слово, позволяющее отличить в мире зависимостей числовую функцию или просто функцию.

"Образ" функции был заложен нами в начале урока, что же мы добавим в схему, чтобы действительно нарисовать портрет "Функции".

к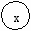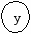аждому f единственное задаем считаем

Т.4 Что будет обозначать запись у = f (х), f (х)

Найдите в тексте.

Работа с таблицей "Образ функции"

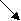
x 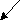1; 3 2 -3



4x-1




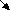
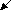
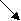
аппарат



4x² - 1




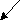
y 3 11 15 35

Что же может делать наш аппарат?

• мы можем "закладывать" разные числа и получать разные результаты
  
• какие модели позволят заложить "неравные" числа, а получить одинаковые результаты (числа противоположные х^{2п ‌}х‌
  

Но - сможем ли мы заложить одни и те же числа, а получить разные результаты?

Нет

Вывешивается схема

В функциональных зависимостях нельзя

В соответствует ли наш вывод определению?

Да, каждому х единственное значение у!


числовая функция

числовая f

оператор
		функционал

числовая функция

число

Не следует смешивать функциональную зависимость величин с причинной зависимостью. Хоть путь, проделанный падающим камнем находится в функциональной зависимости от времени, то причиной падения камня является не t,

а F земного тяготения.

Первичное закрепление

математического определения функции.

Задание классу:

Художник перепутал картинки с функциональными и нефункциональными зависимостями.

Ваше задача определить к какой группе они относятся.

Быстрее это сделать безусловно поможет определение и "небольшая инсценировка его".

Учитель ^{рукопожатие} Ученик

х у

независимая зависимая ( от знаний учителя)

"Я могу поздороваться, пожав руку ученику (левую - правой, правую - левой, левую - левой, правую - правой - каждому х - единственный у).

Я могу поздравить своего ученика с победой, пожав двумя руками его левую или правую руку. Но я не могу одной рукой пожать его две руки одновременно!".

Ведь для разных х может быть один у, а наоборот нельзя!" (возвращение к таблице)

Является ли зависимость функцией и почему?

у=f (х) у=f (х) у=f (х) у=f (х)

да нет да нет

Если есть затруднения модель

пассажир - кресло

Вернемся к нашей проблеме. Чтобы дать ответ, послушайте слова Н.И. Лобачевского:

"Общее понятие требует, чтобы функцией от данного х называть то число, которое дается для каждого х и вместе с х полностью меняется".

Функциональная терминология.

Алгоритм изучения любого вопроса в геометрии вам известен. Перенесем его и на алгебру.

История. Определение. Терминология. Свойства. Приложение.

Терминология.

В
оспользуемся методом аналогии.

Найти: Выражение, уравнение, ОДЗ

Ф






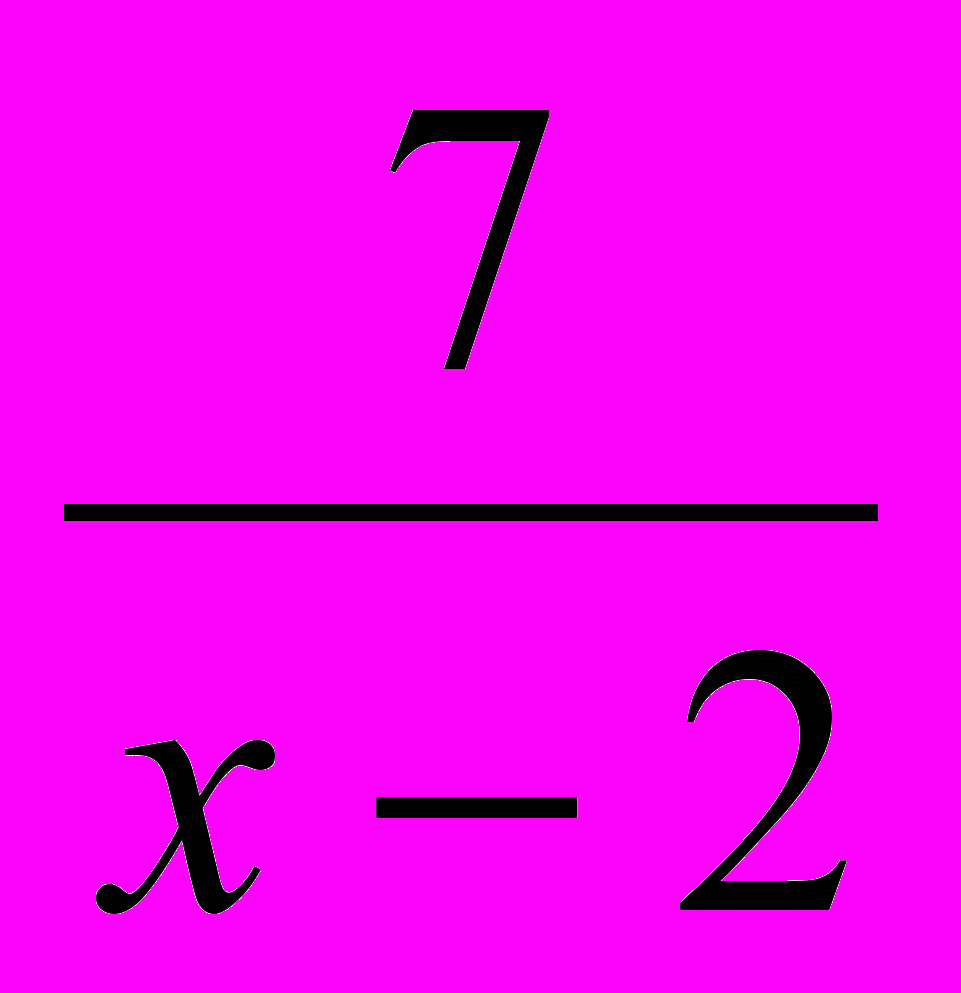
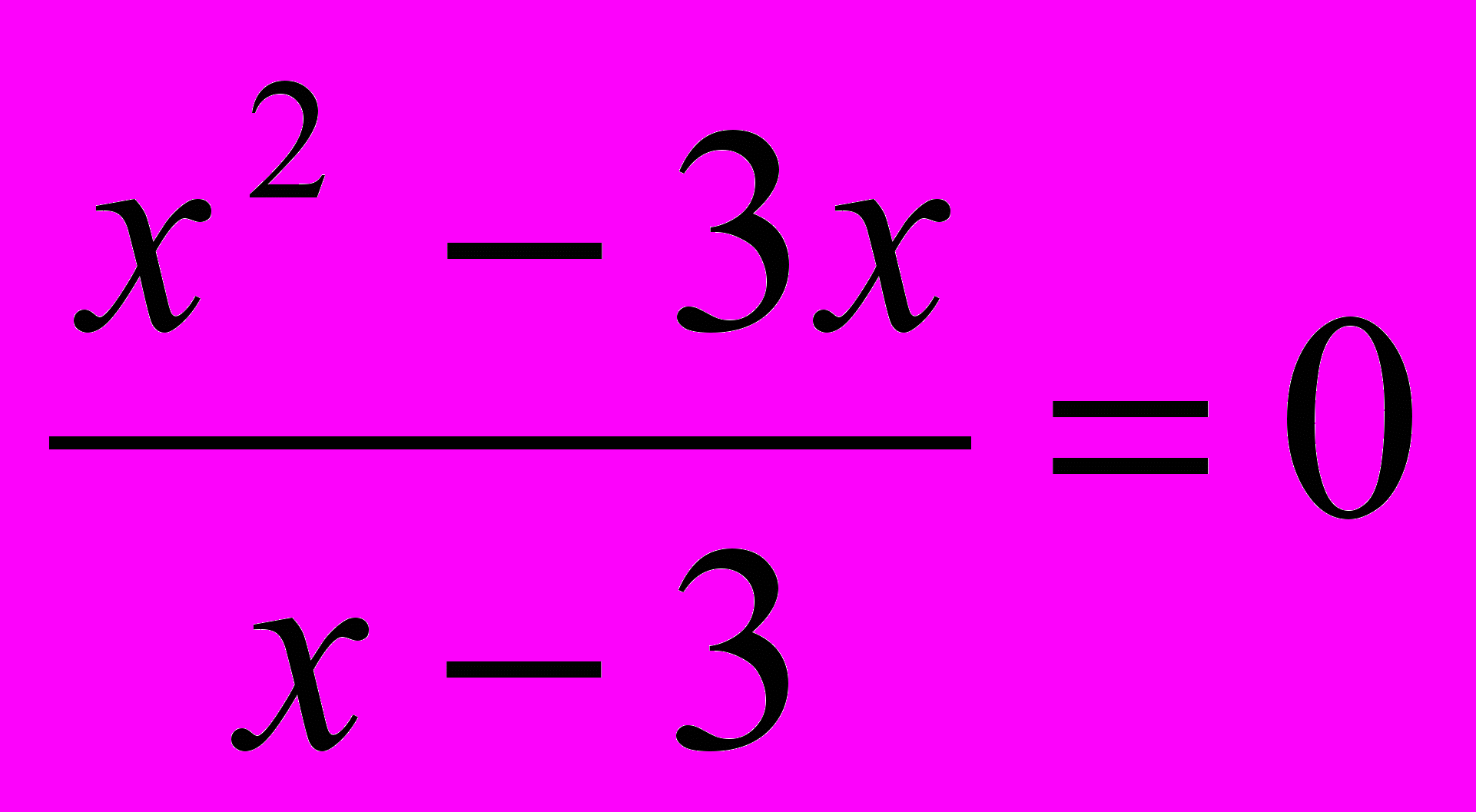
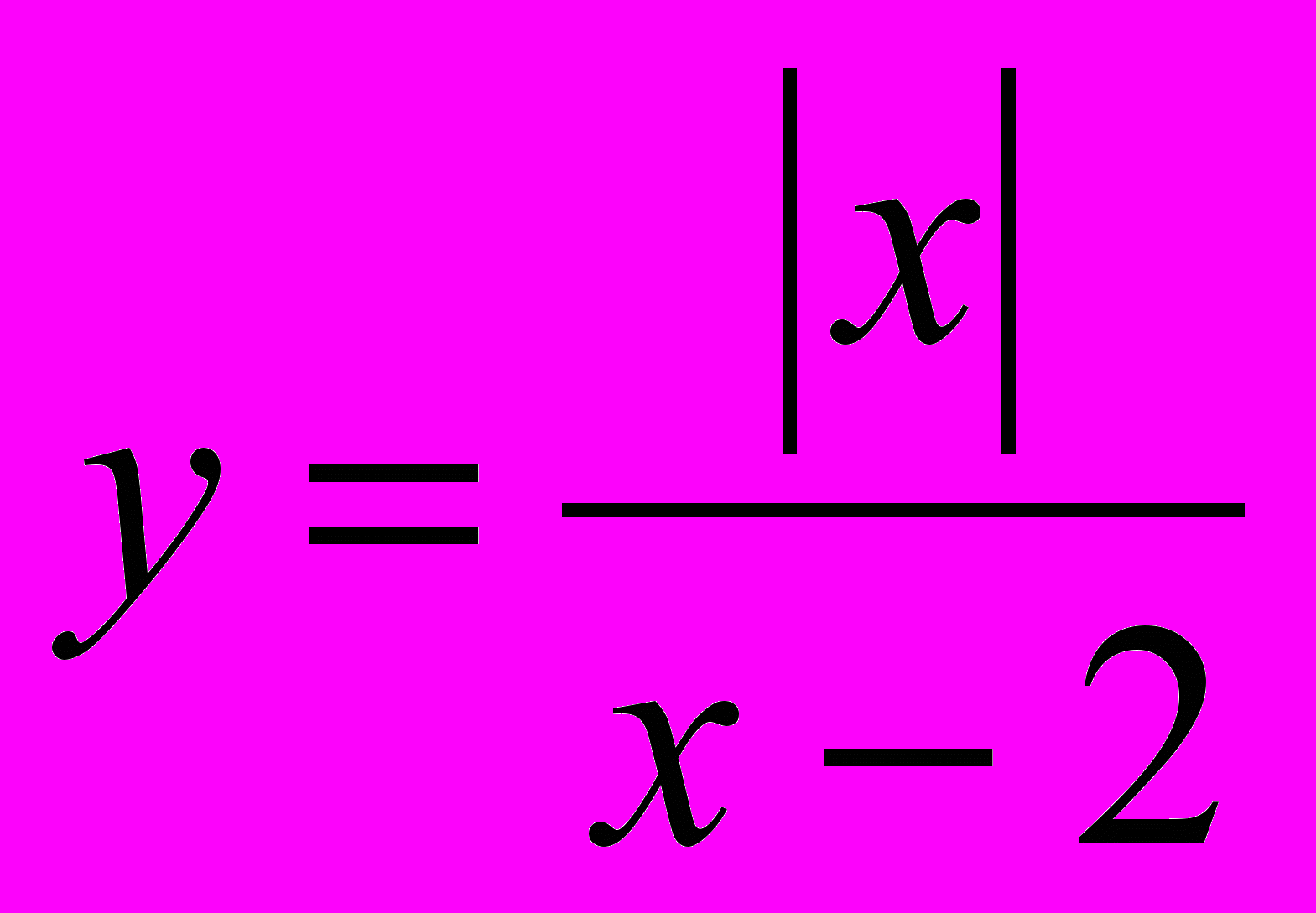
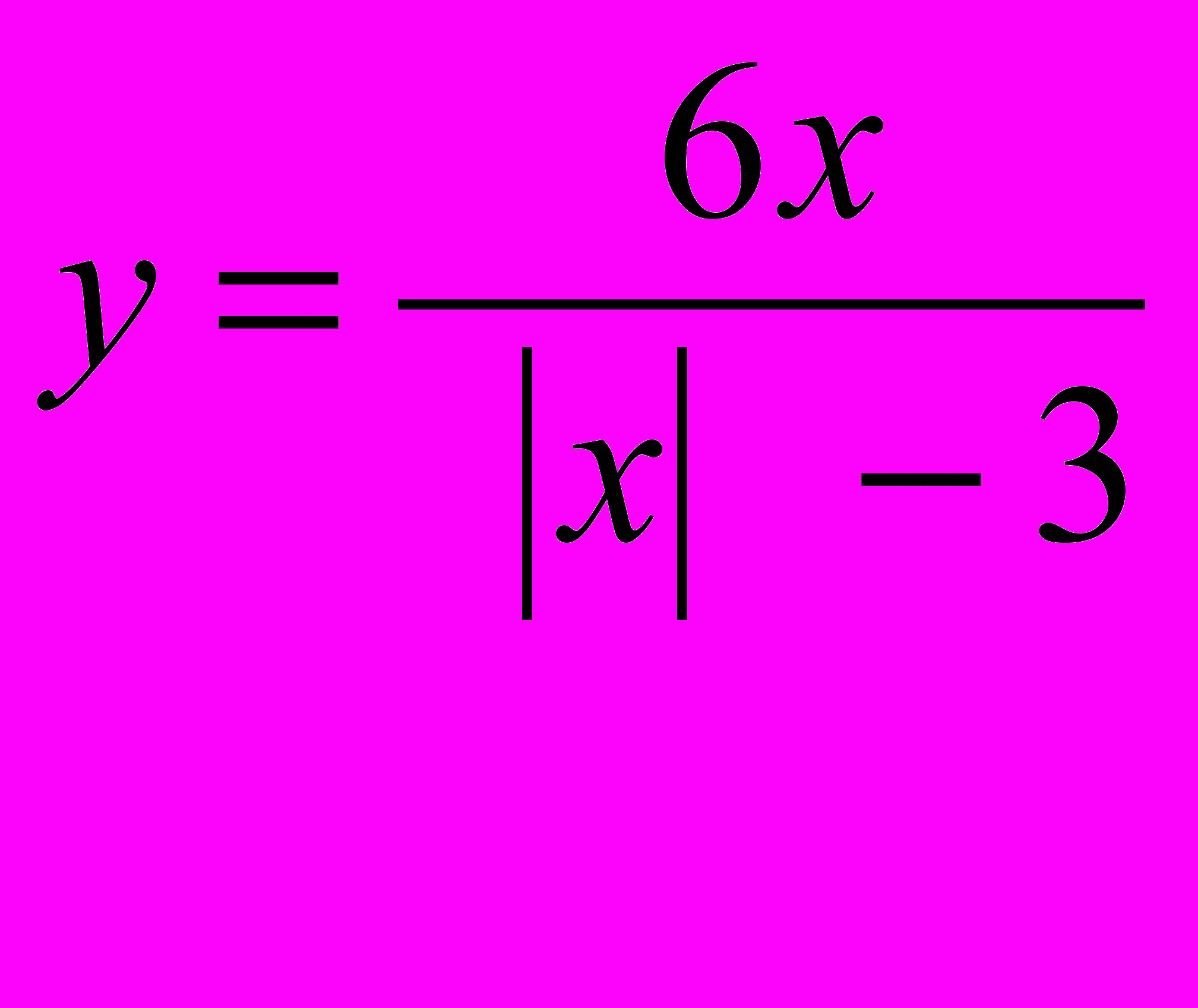
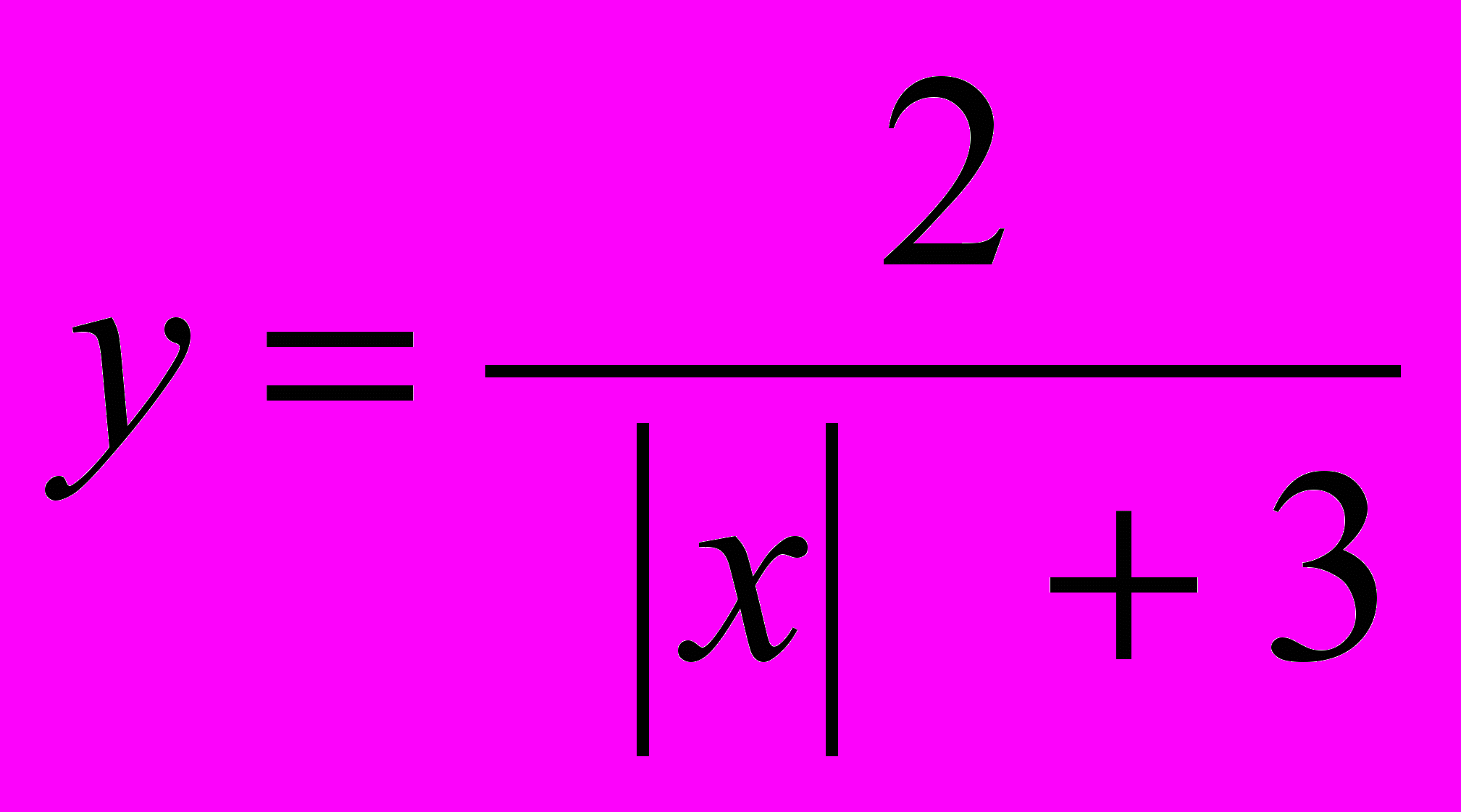
ункция , область определения

М


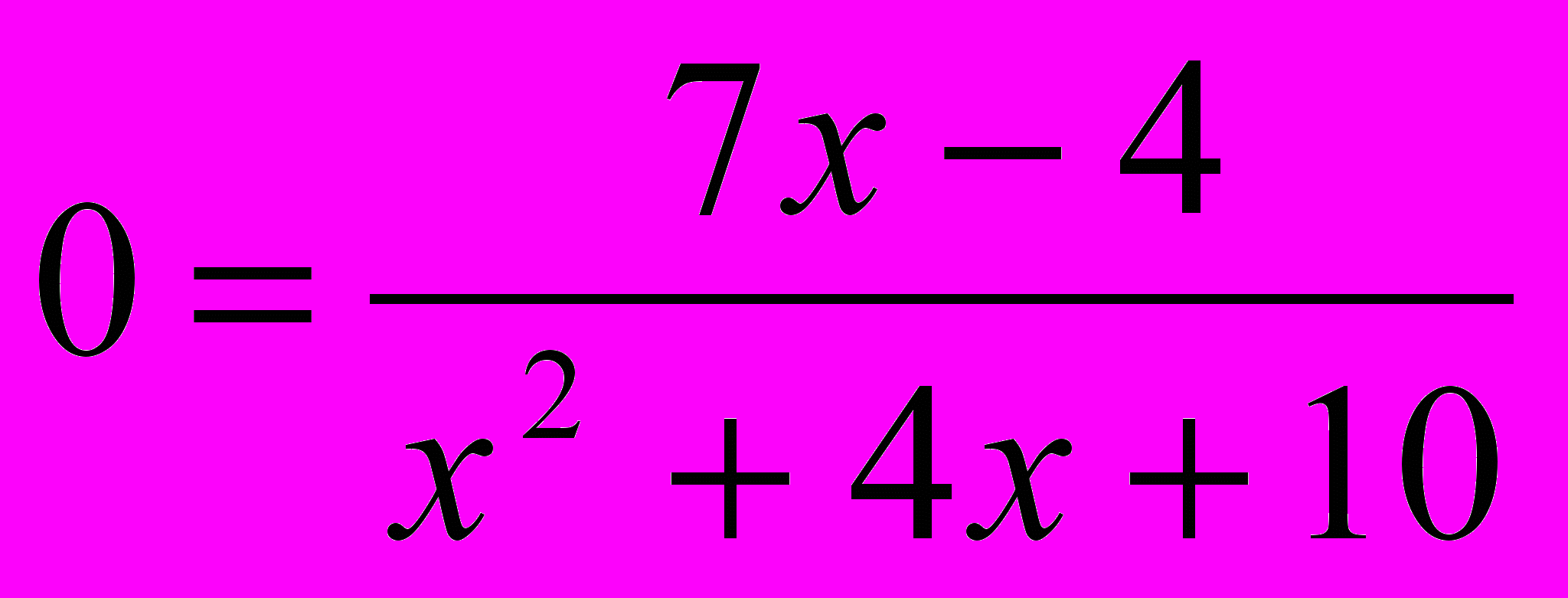
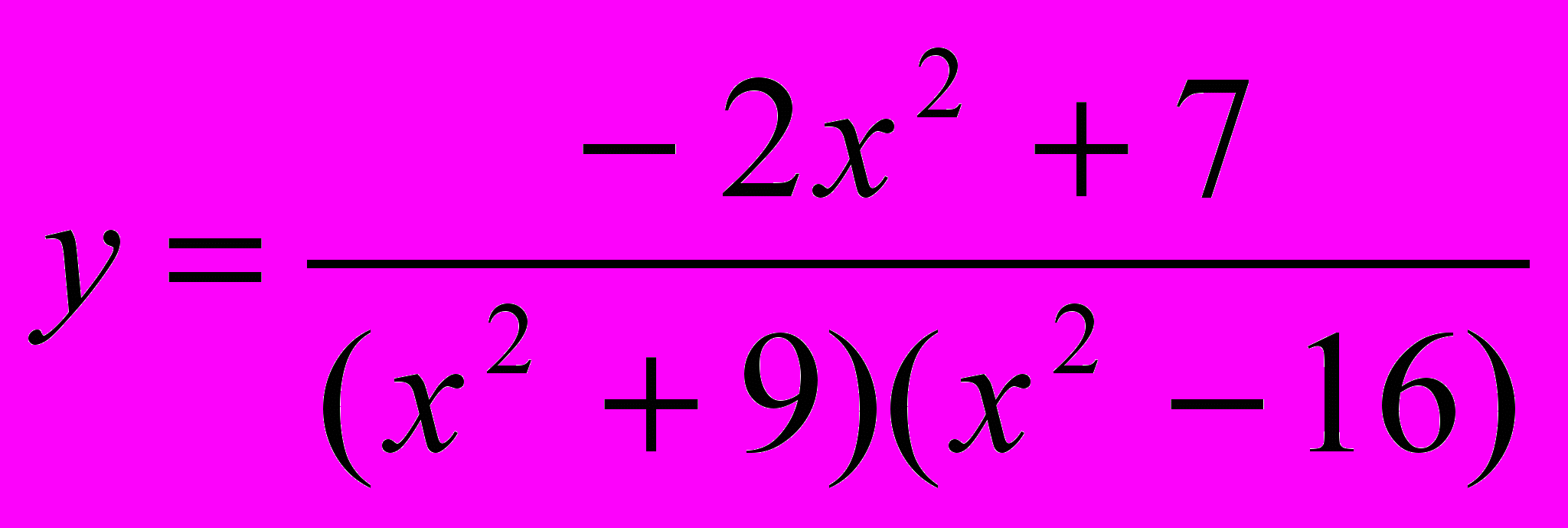
ы с вами устанавливаем "единственную" область определения функции.

Но иногда она может быть задана.

Прочтите текст №5, после чего необходимо будет ответить на ряд вопросов.

у=х² D(у)=R, так как функция задана формулой, значит Д (у) - множество всех значений переменной, при которых эта формула имеет смысл.

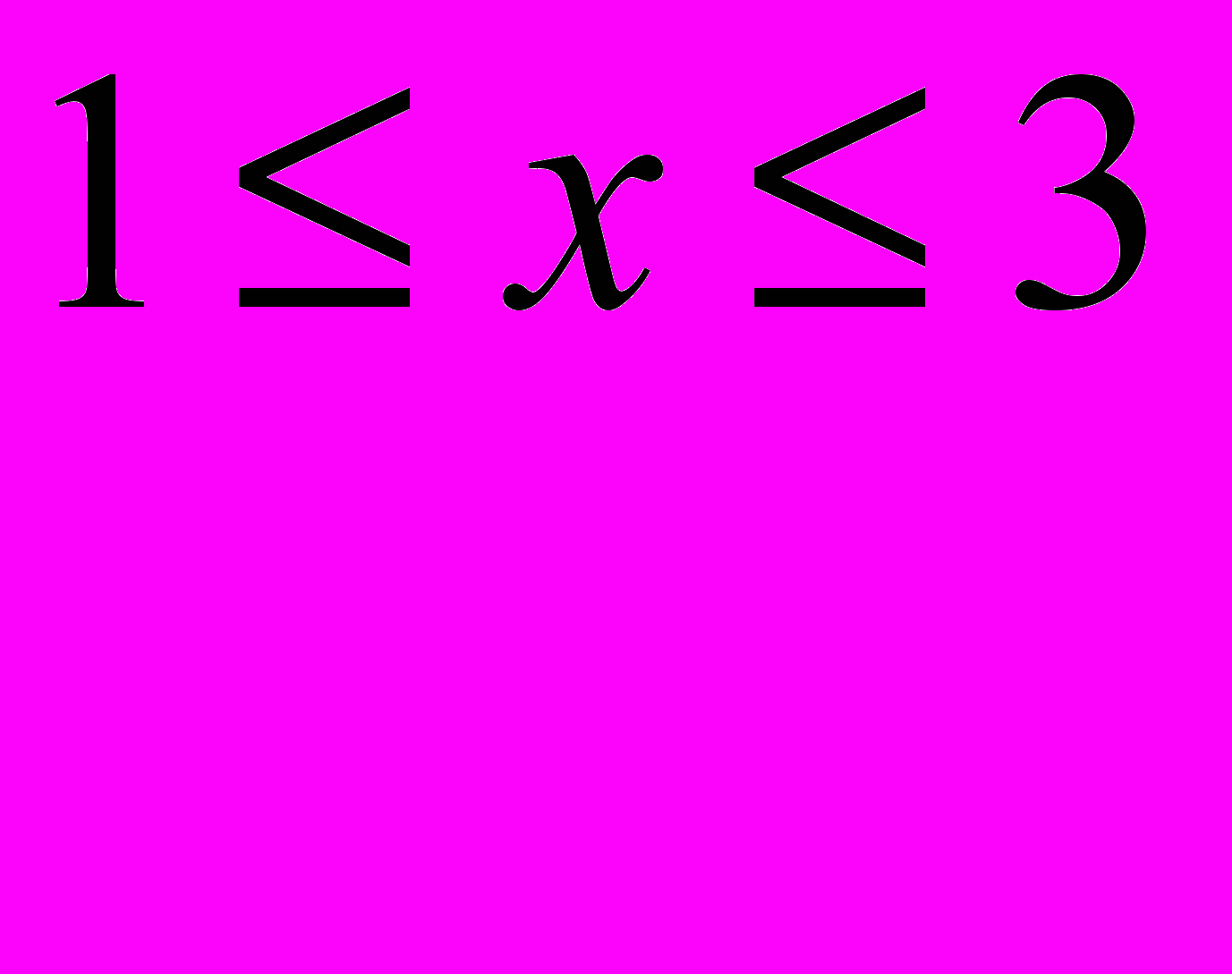
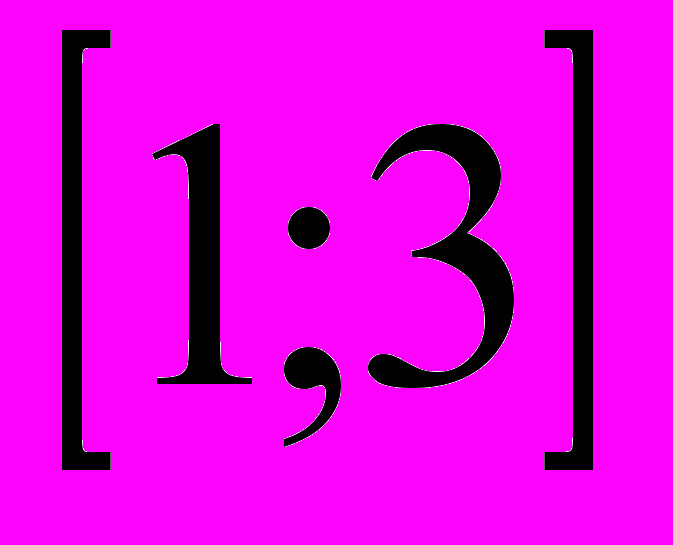у=х² Д(у)=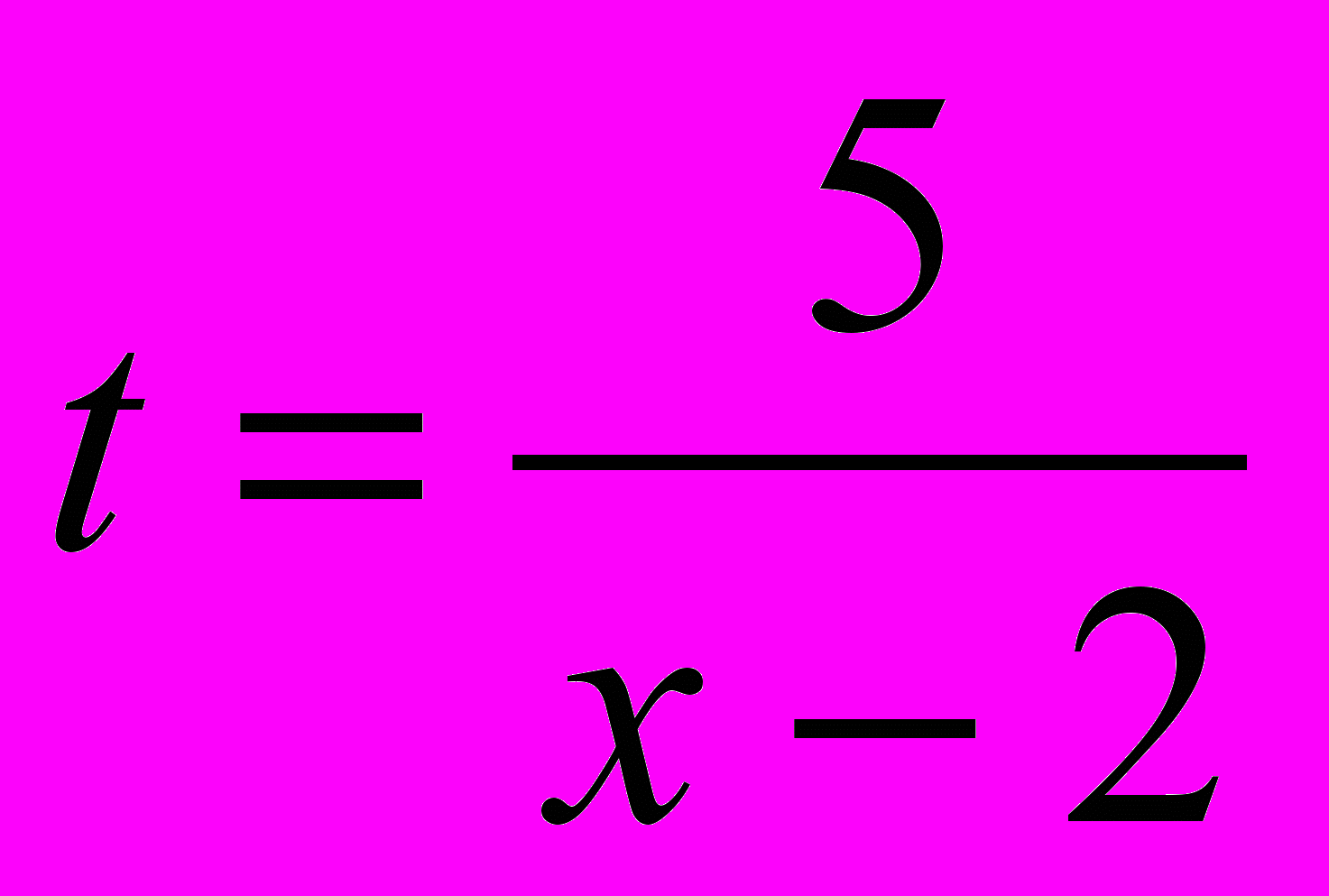



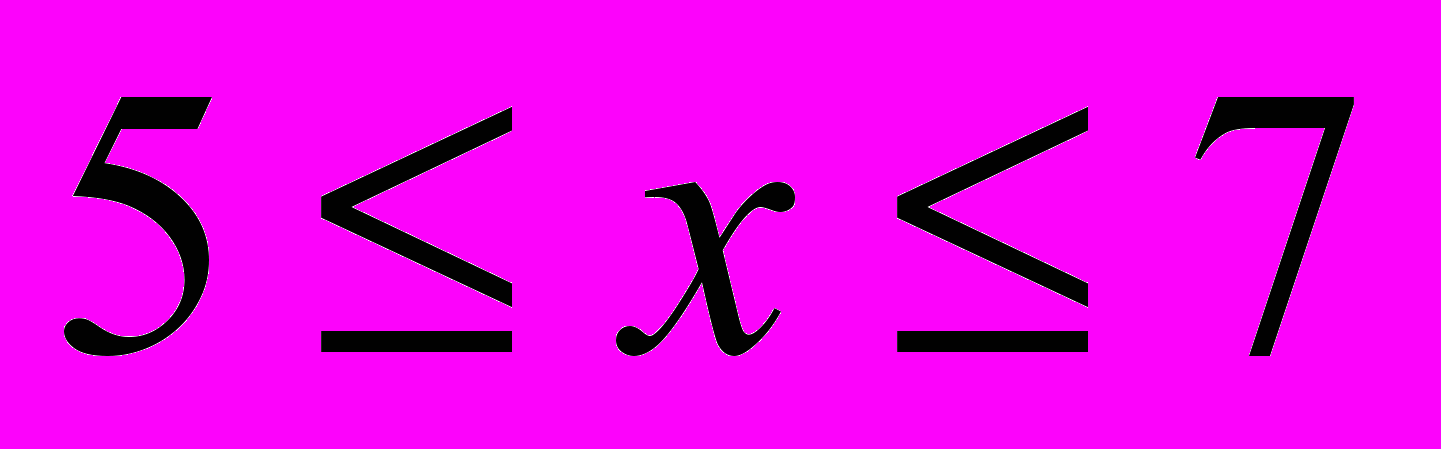
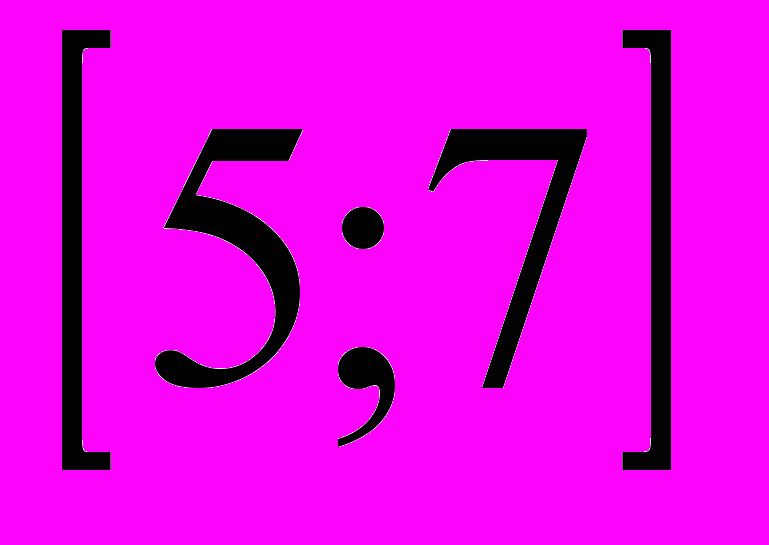
Д(t)=


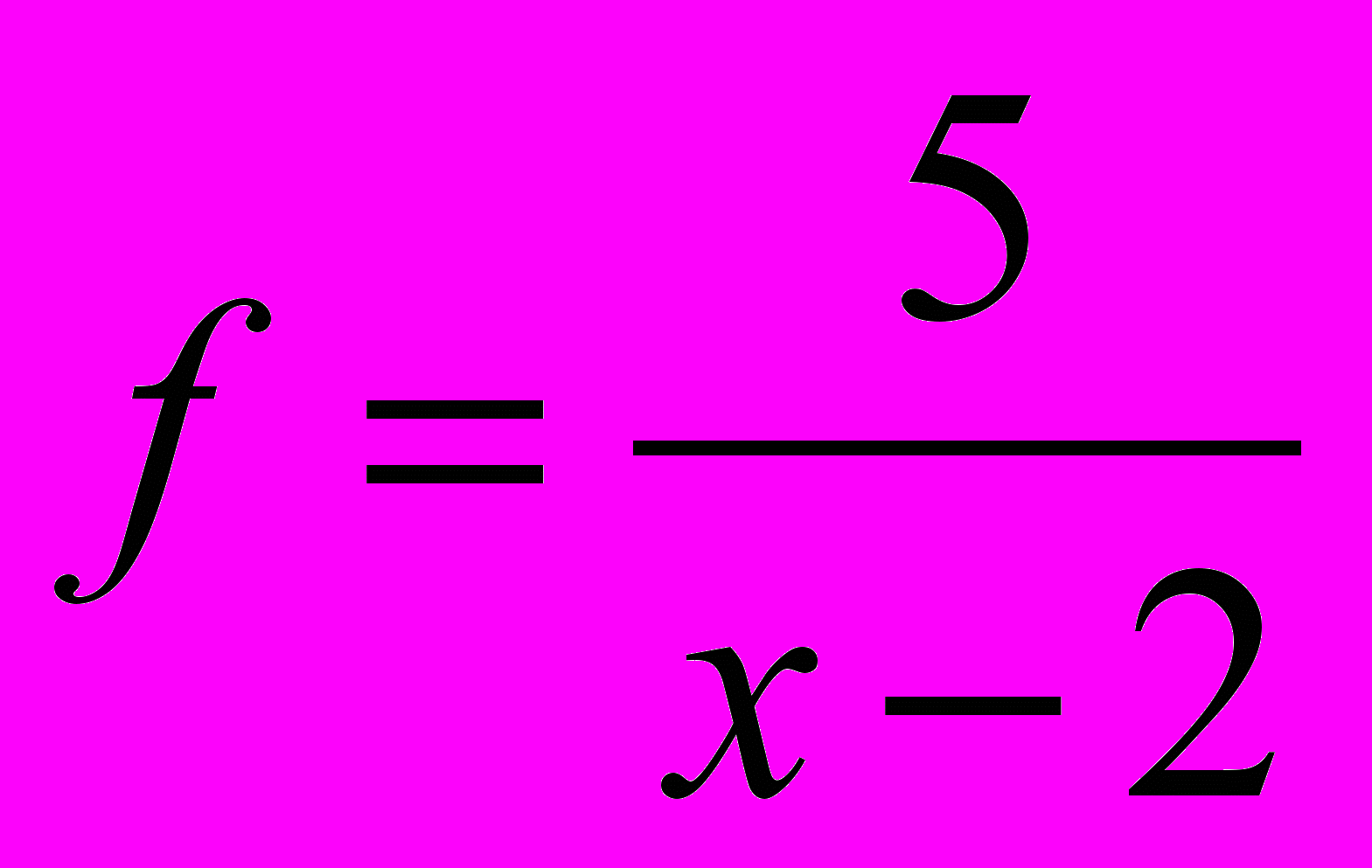
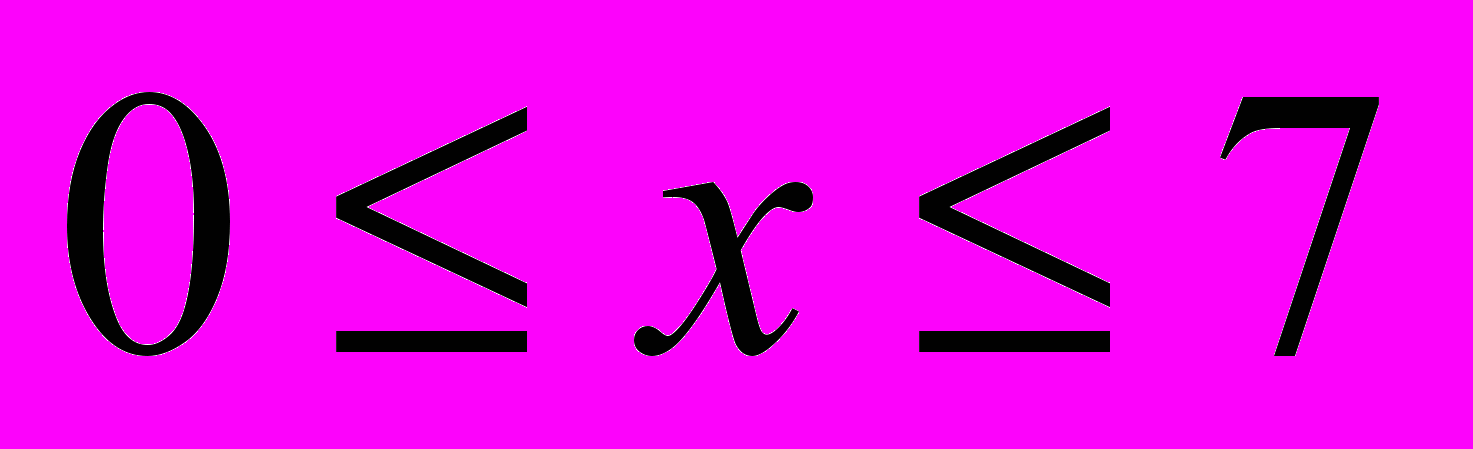
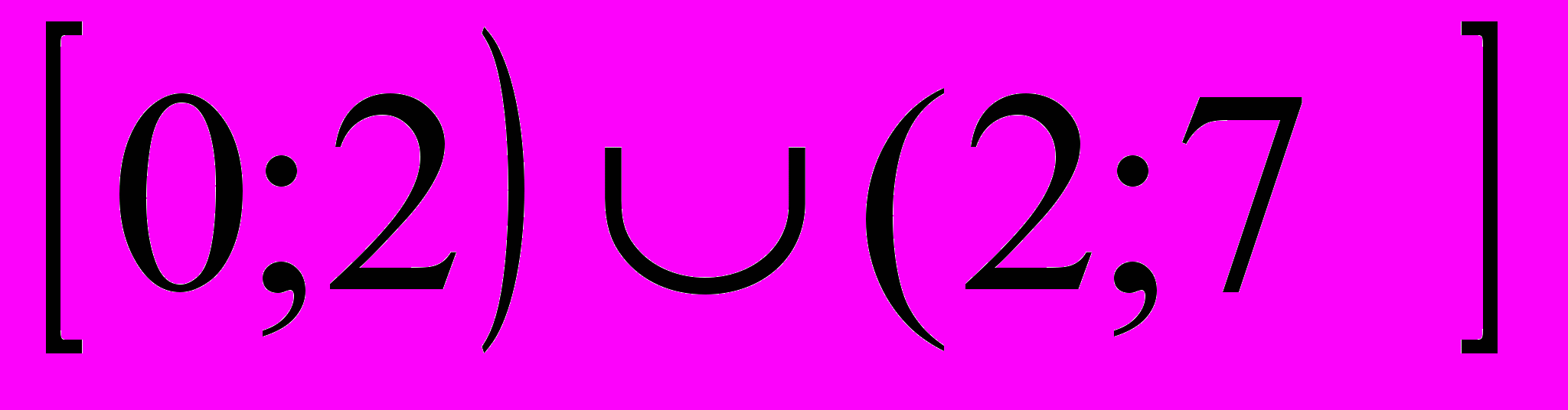
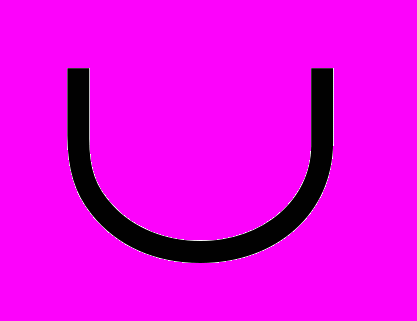D(f)= объединение




В книге "Математика в понятиях, определениях и терминах" я нашла интересную фразу (стр. 302)

"Иногда область определения Х функции называют областью отправления или источником, а множество значений У называют областью прибытия или целью".

И действительно, именно так и работает наш аппарат "Функция" (возвращение к таблице).

Настало время провести небольшую исследовательскую работу, а именно выяснить способы задания функции.

В предложенных примерах укажите D(у), Е(у)

1 пример мы разберем вместе.

Текст - таблица № 6

Пример. D(f) Е(f) Способ задания

1. к
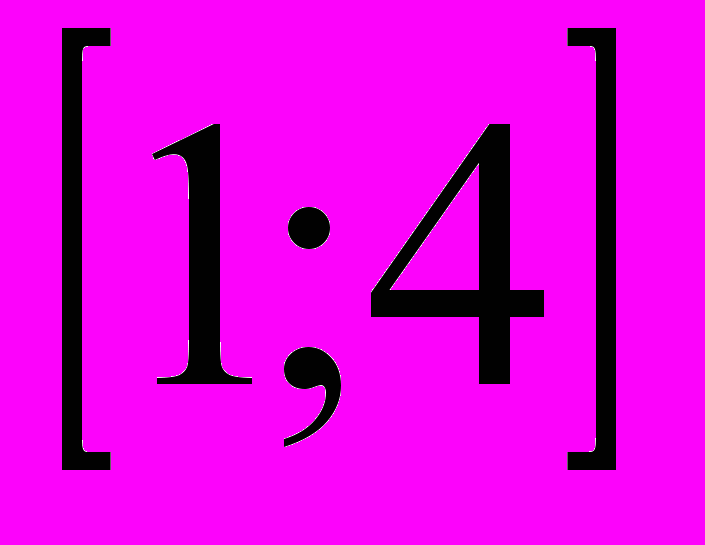
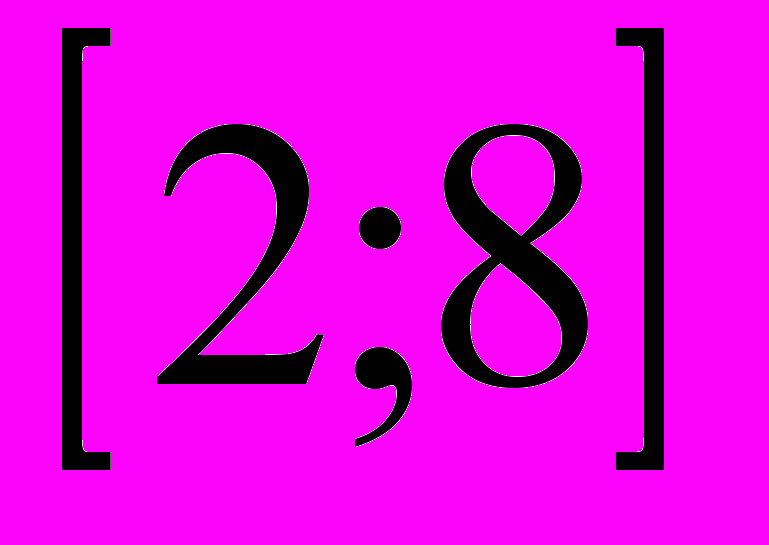   олич. 1 2 3 4 таблица
   

стоим.(р) 2 4 6 8

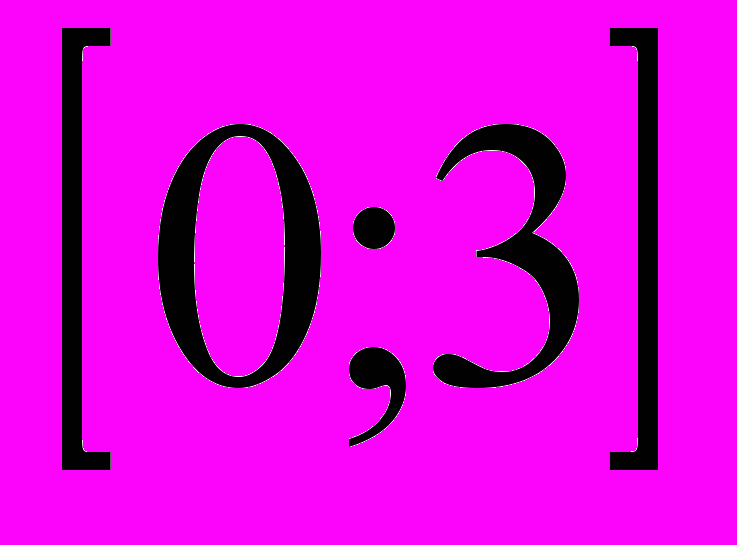
2. V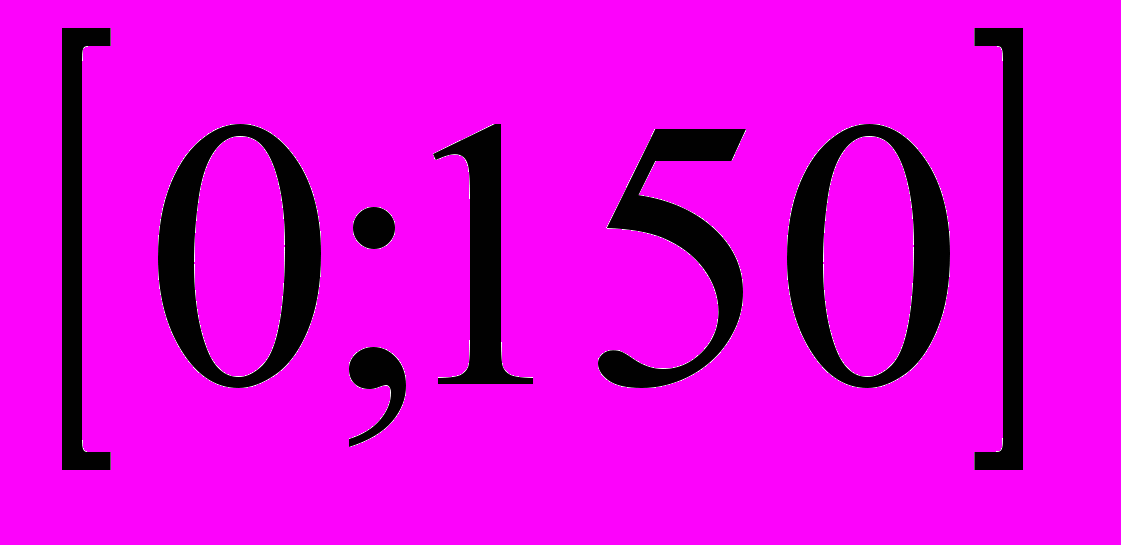=50 км/ч формула
   

S=50 t

ехал 3 часа

3.

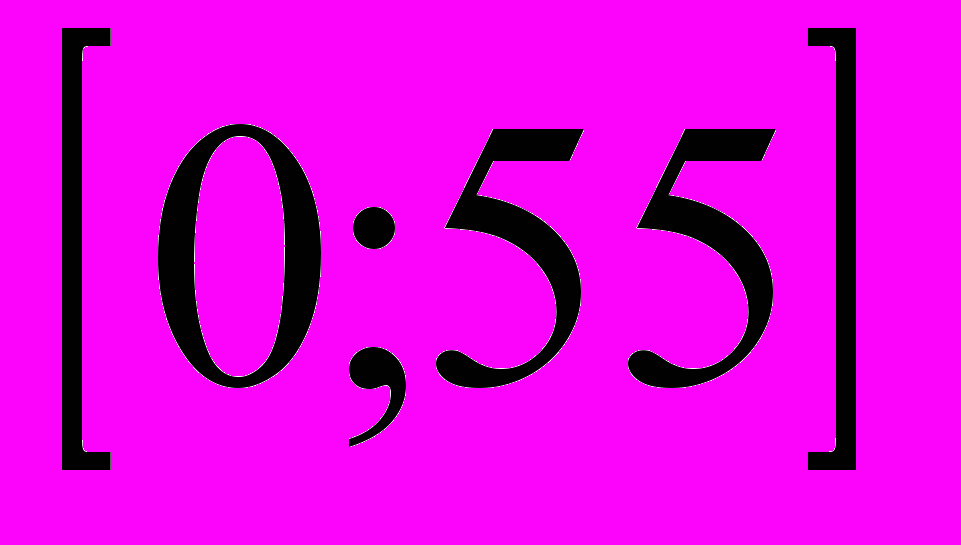
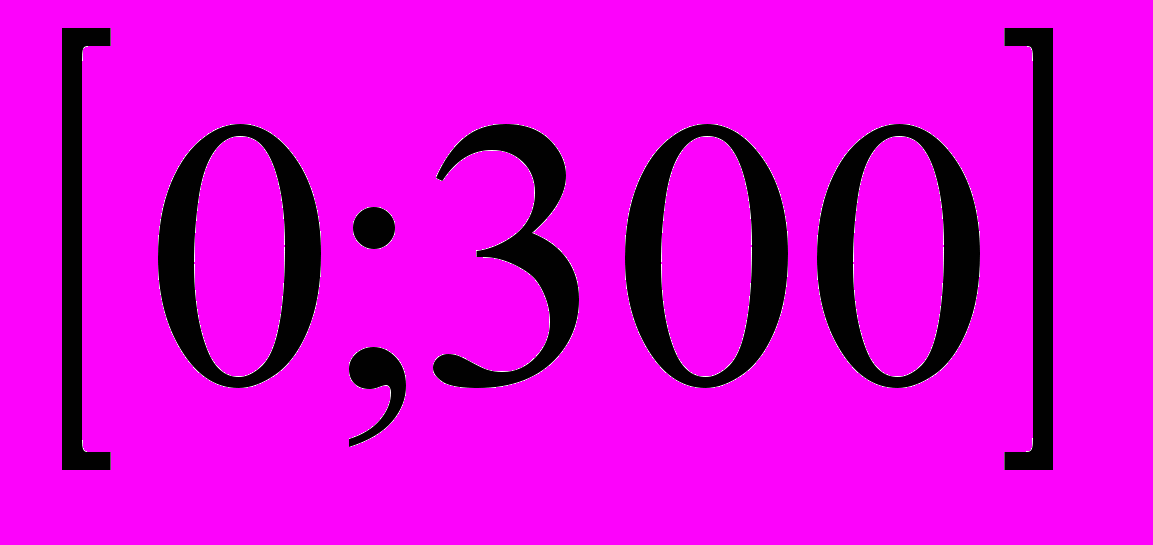4. график, словесное описание


Вставьте пропущенные данные в словесное описание графика

" Я иду до школы… минут. При этом мой путь близок, всего лишь … метров. Весь первый урок (… минут) я вспоминал: "Не забыл ли выключить утюг?" Со звонком я помчался домой. Через … минут убедился: "Все в порядке".

Убедитесь, сравнив свои исследования с научным текстом.

Вставка - научный текст № 7. Сделайте вывод.

Итак, функция может задаваться одним или несколькими аналитическими выражениями (формулами), таблицей, графически, графами ( ) и т.д.

Лишь бы был задан закон однозначного соответствия.

Вторичное закрепление понятия "функция", функциональной терминологии.

"Да, способов задания много. И в каждом, я должен уметь узнавать именно функциональную зависимость, - подумал В. Верхоглядкин".

Ну что же, попробуем и мы,

Практикум.

Определи, какие зависимости являются функциями.

Помощь: каждому х - единственное значение у.

(нельзя! одному х - 2 и более у).

Допиши свой пример зависимости, которая не является функцией.

а) х 1 2 3 t 1 1 3 х -3 6 3 х 1 2 3

у 3 4 5 v 3 4 5 z 2 4 2 f 4 4 5

б) у=2х у= 5х-7 х²+у²=25

Помощь:

у=7 х=3 при х=3, найти у

в) Прежде чем мы приступим к 3 способу, проведем физкультминутку "Зрение".



Перед вами графики зависимостей, спроецируйте их мысленно на переднюю стену класса, каждый по 3 раза

Общий подход к поиску: а у, график только в одной точке - функция!

г) у=х+5

а) Словесная модель.

б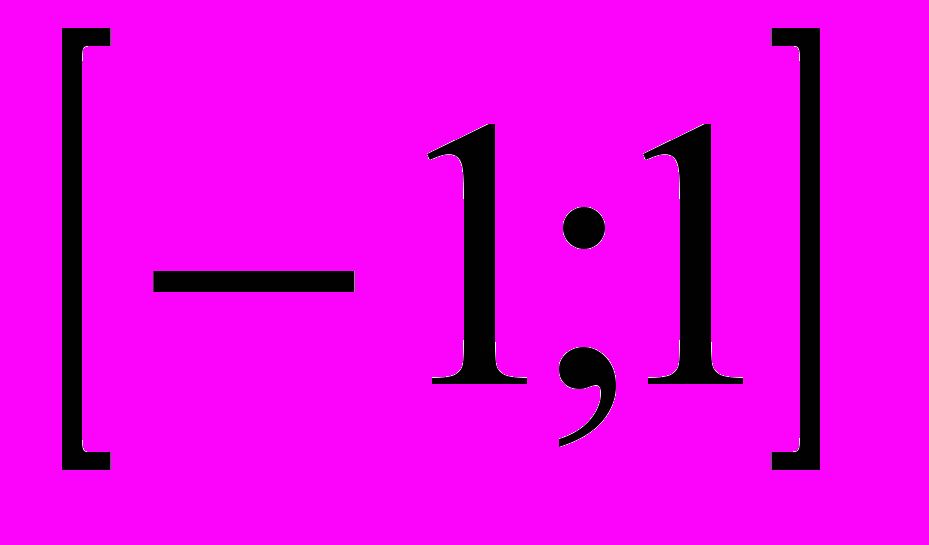) При каких значениях аргумента линейная функция положительна? отрицательна? обращается в о?

в) Найдите наибольшее значение функции на промежутке (6)

наименьшее - (0)

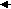
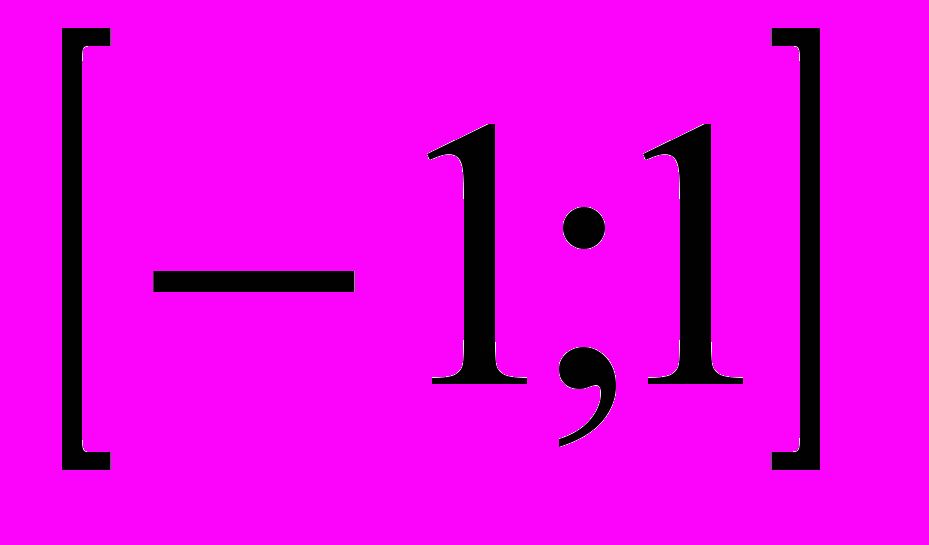наиб. наим.

6. 4
   
7. -
   

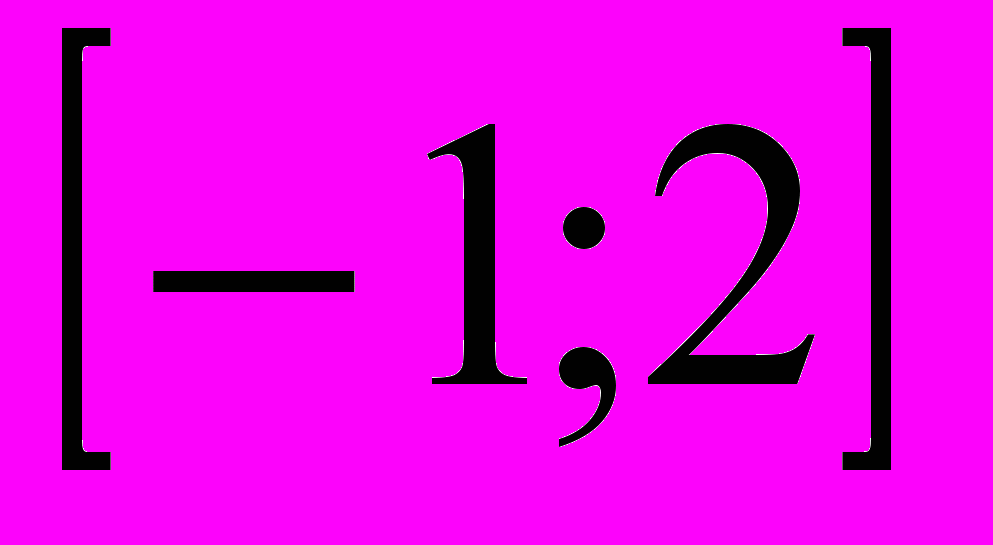
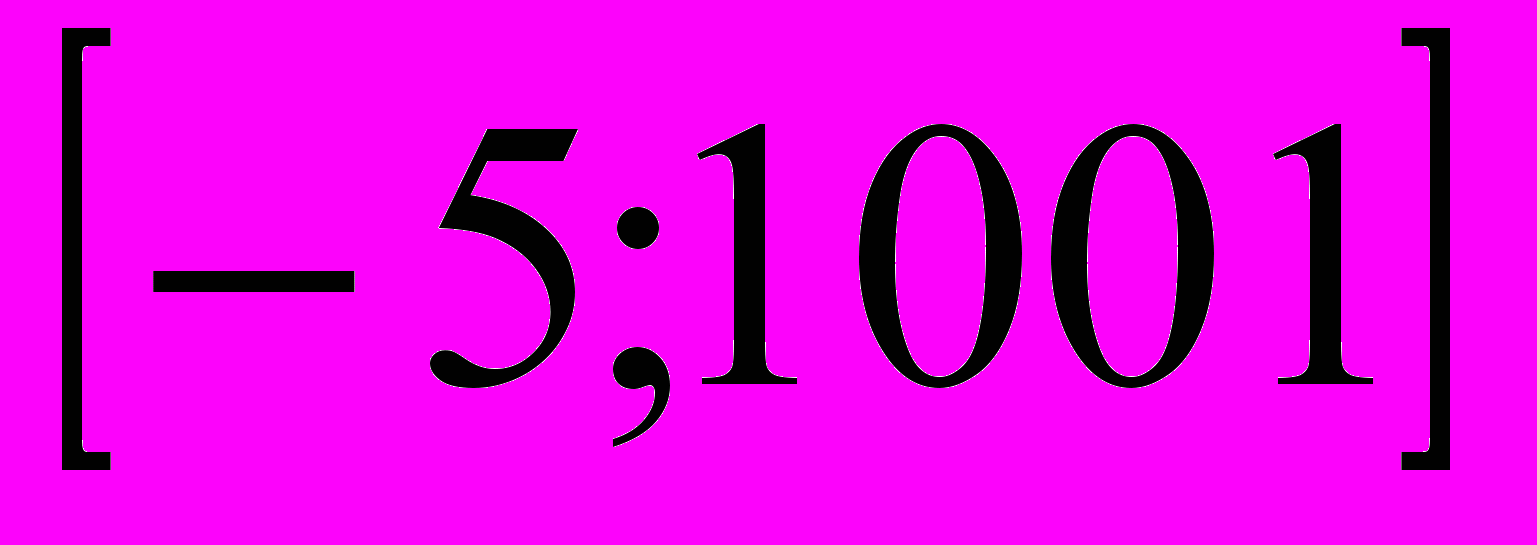- 0

Желаю вам, чтобы и в 10 классе (учебник Колмогорова, стр. 27) вы бы так же успешно ответили на эти вопросы.

(В случае затруднений: "Я думаю, что к 10 классу такие задания затруднений не вызовут".)

г) Изобразите на координатной плоскости как можно больше точек, у каждой из которых разность ординаты и абсциссы равна 5. (30 сек)

у - х = 5

у = х + 5

Сзади на доске изображен график линейного уравнения у - х = 5. Надеюсь, что у вас в тетрадях получился такой же.

1. Найдите "графические ошибки" автора чертежа.
   
2. Выразите в формуле линейного уравнения у через х
   

у = х + 5 - формула, задающая линейную функцию.

И это тема следующего урока.

д) При каких значениях х функция у = х ( х - 1) обращается в нуль?

е) Какой из графиков соответствует функции, заданной следующим описанием:

"Если взять число х, умножить его на 4, отнять от результата 4 и разделить результат на 4, то получится у".

Проверка усвоенных понятий .

Расширение знаний.

Аукцион "Что можно узнать?"




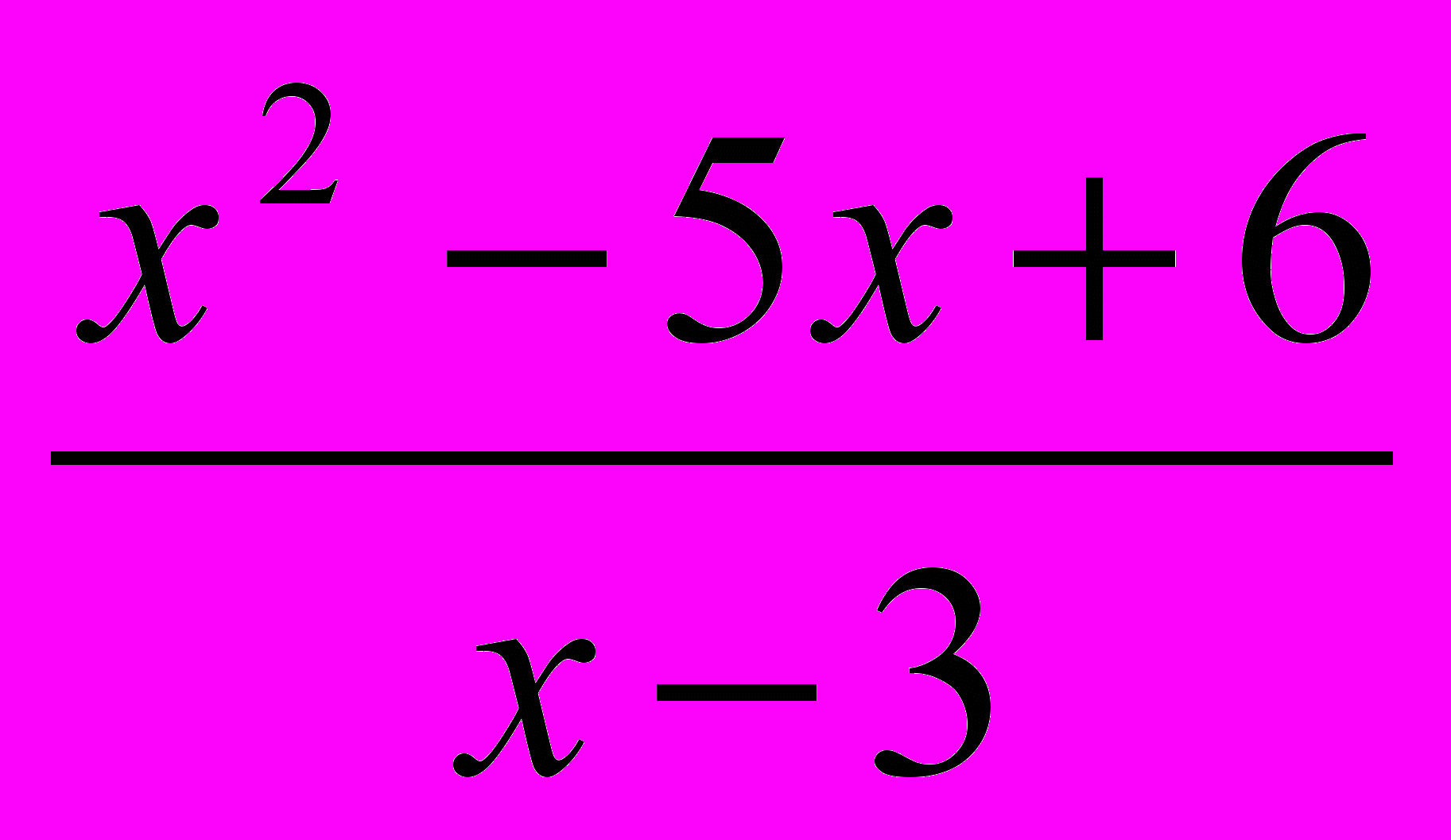
f (х) =

1. зависимость
   

2.



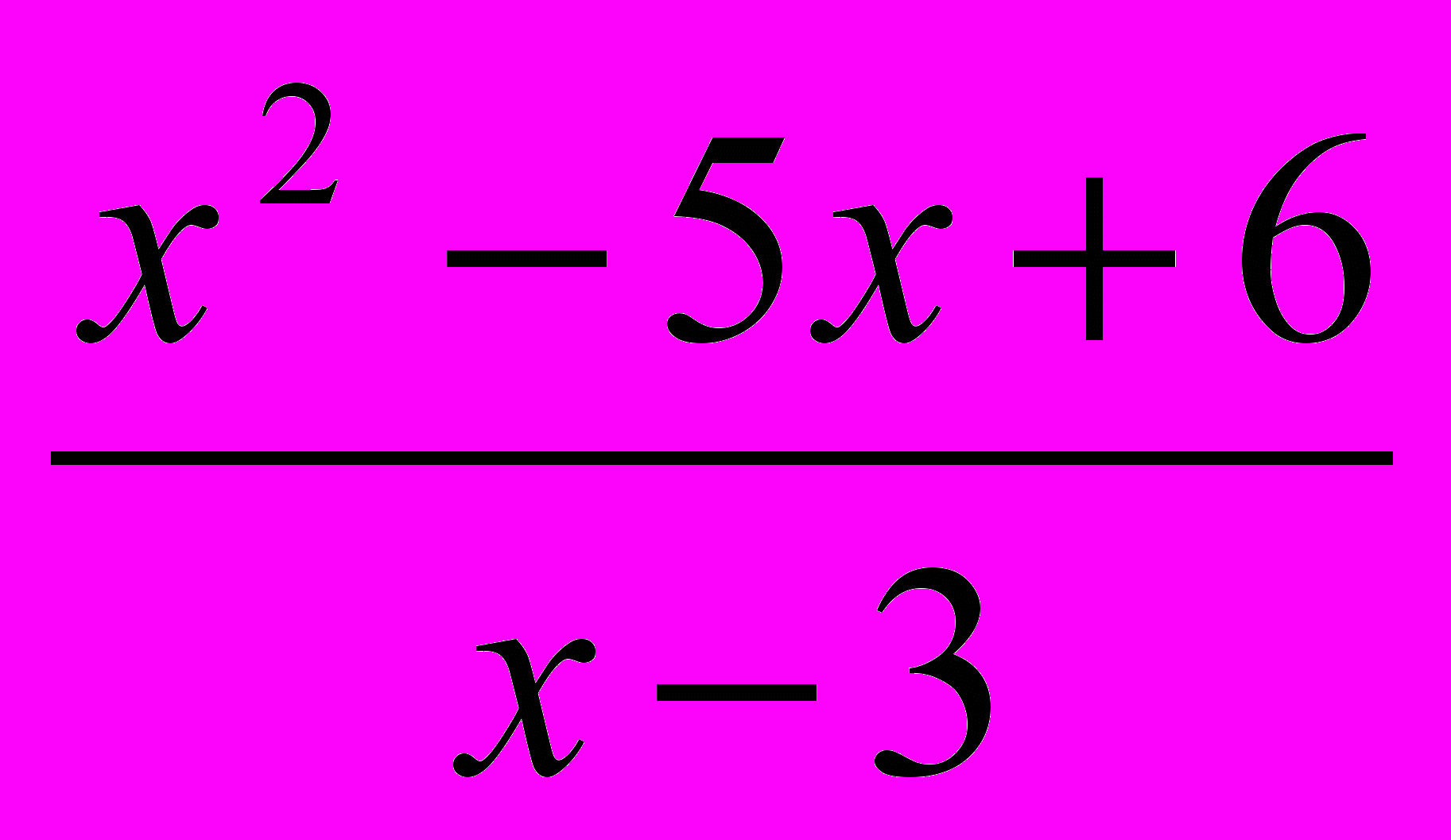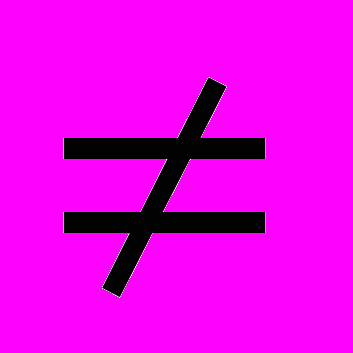
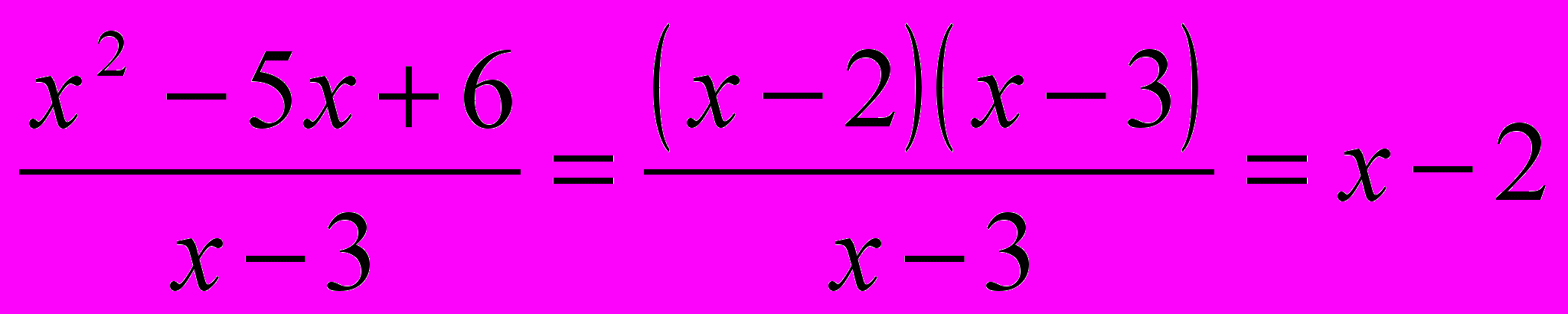
ОДЗ: х 3

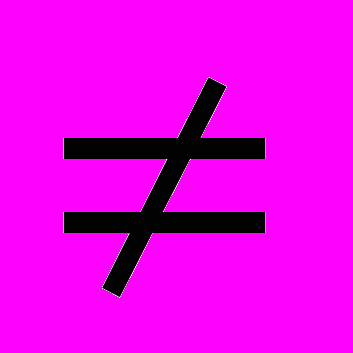
3. f (х )= х - 2, х 3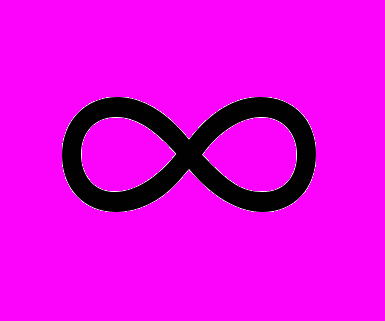

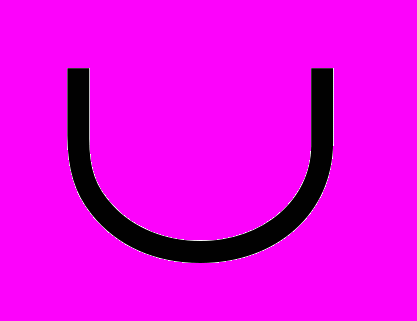
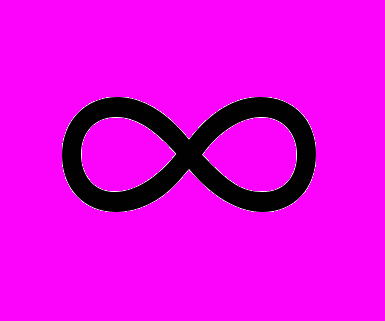D (f ) = (- ;3) (3; + )

Е (f ) = (- ;1) (1; + )

4. После построения чертежа

5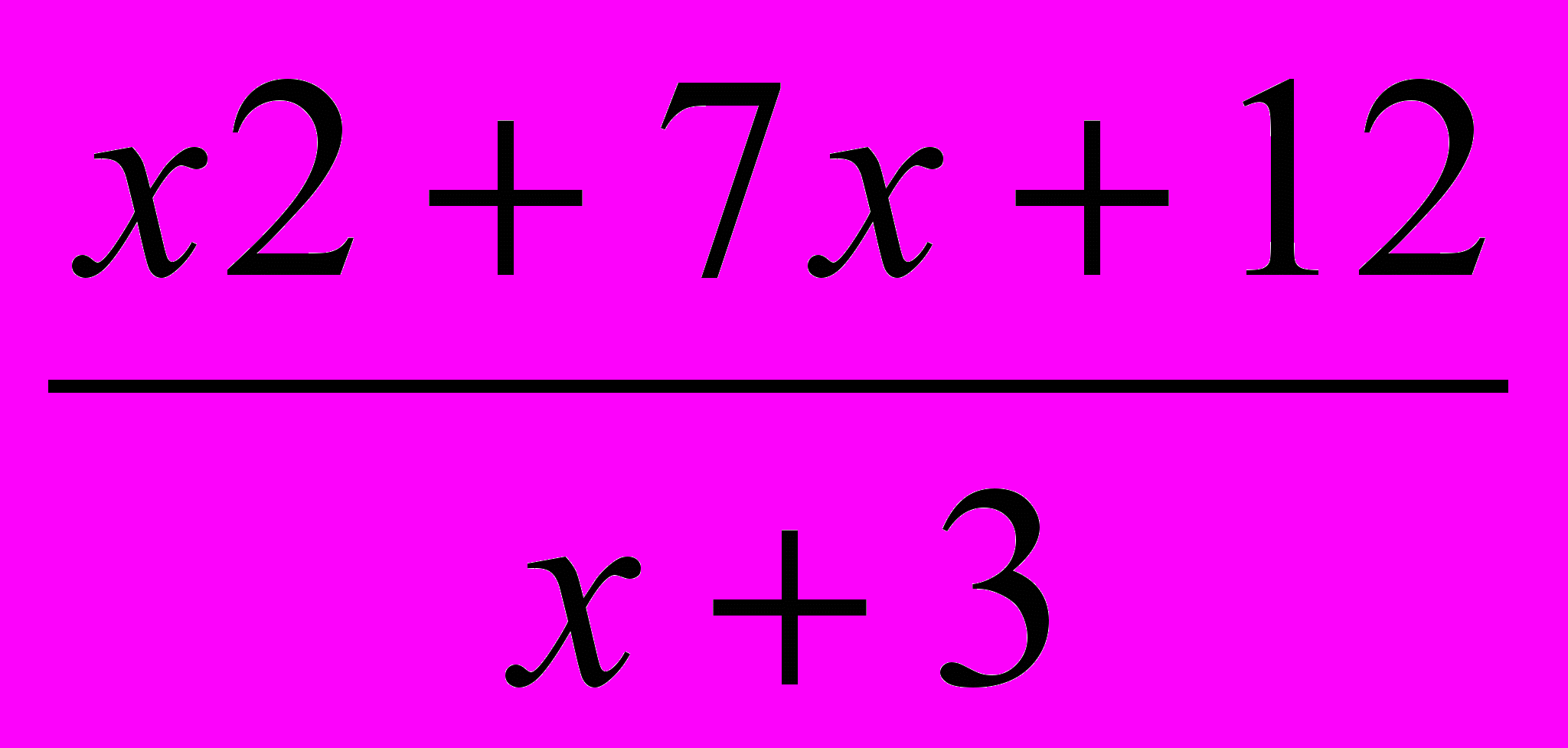. Функция.

Дома: z(х)=

и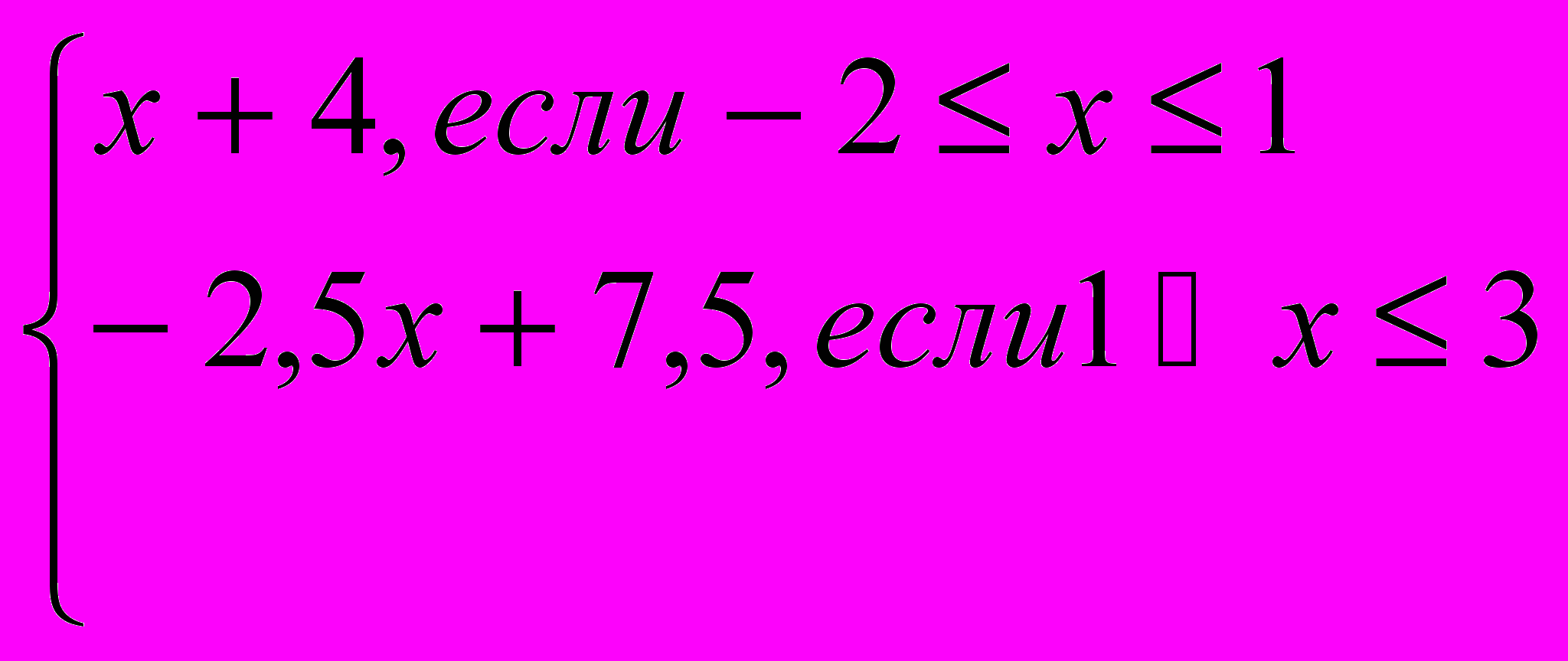сследовать зависимость

f(х)=

D (f), Е (f), график f (-1) f (0) f (2) f (5)

Большинство зависимостей школьного курса алгебры являются функциями. А соответственно, плавание на 4 ките, поддерживающем науку, должно быть интересным, увлекательным, но и требующем серьезной подготовки.

А сейчас давайте попробуем приоткрыть тайну свойств функции, пока не используя строгих математических определений. А за помощью обратимся к источнику русской народной мудрости - пословицам.

Опорный блок.

Ведь пословицы - это отражение устойчивых закономерностей, выверенных многовековым опытом народа.

1. "Чем дальше в лес, тем больше дров"
   

"Чем дальше в лес, тем больше дров", гласит пословица. Изобразим графиком, как нарастает количество дров по мере продвижения в глубь леса. Горизонтальная ось графика - это лесная дорога. По вертикали будем откладывать количество дров на данном километре. График представляет собой количество дров как функцию пути.

Согласно пословице, эта функция неизменно растет. Какие две точки на оси абсцисс ни взять, для более дальней (чем дальше в лес..) значение функции будет больше (… тем больше дров). Такое свойство функции называется монотонным возрастанием. Математически это записывается так: х₁< х₂ f (х₁) < f (х₂) для всех х, входящих в область определения.

2. Придумайте антоним ко 2 слову
   

монотонное убывание

Какую пословицу можно было бы подобрать?

"Мать не слушать, добра не видать"

(меньше послушания, больше зла и больше зла меньше послушания)

3. "Выше меры конь не скачет" "ограничена сверху"
   

4)"Пересев хуже недосева"

"Максимум" "Минимум"

Наиб знач.f Наим. знач. f

у _max = у (а) = в

5. "С высокой горки больно падать, да все равно подниматься"
   

"Научись встречать беду не плача:

Горький миг - не зрелище для всех.

Знай: душа растет при неудачах

И слабеет, если скор успех."

Пословица "Пересев хуже недосева". Вековой опыт свидетельствовал: урожай лишь до некоторой поры растет вместе с плотностью посева, дальше он снижается, потому что при чрезмерной густоте ростки лишь начинают глушить друг друга. Эта характерность станет особенно наглядной, если изобразить ее графически, где урожай представлен как функция плотности посева. Урожай максимален, когда поле засеяно в меру. Максимум - это наибольшее значение функции по сравнению со значениями во всех соседних точках. Это как бы вершина горы, с которой все дороги ведут только вниз, куда ни шагни. Максимум здесь локальный. Математически это значит: существует некоторая (а - б, а + б) - окрестность точки х = а такая, что для всех х из области определения функции, входящих в эту окрестность, выполняется условие: < б f (х) < f (а).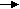

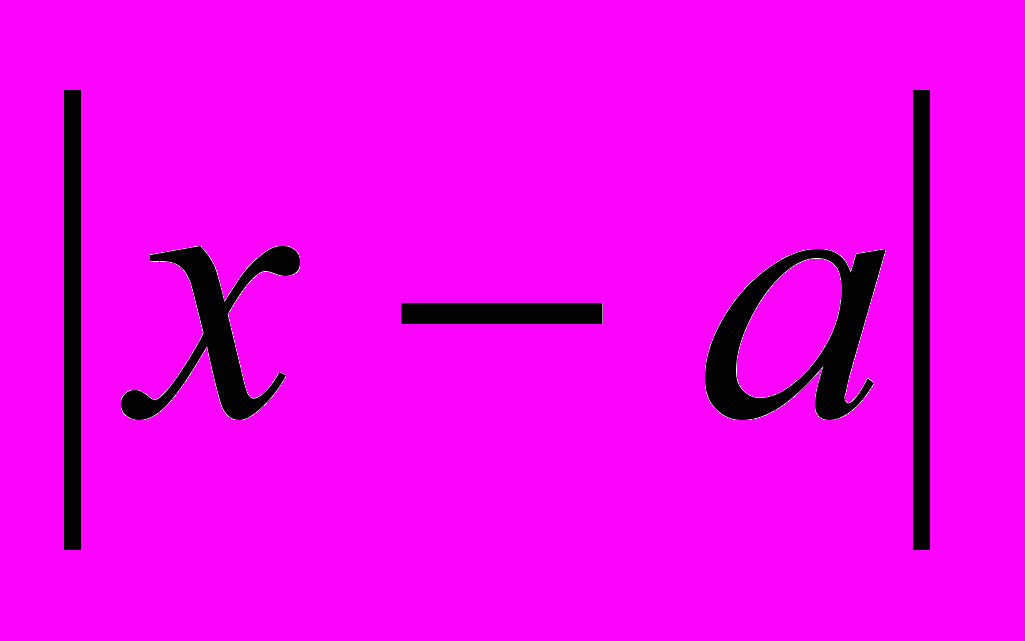Есть у максимума антипод - минимум. Минимум - это как бы впадина, из которой куда ни шагни - все дороги ведут только вверх, т.е. для всех х D (f) (D(f) - область определения функции) выполняется условие: < б f (х) > f (а). Все значения функции из 2 б - окрестности точки х = а больше по сравнению с минимумом. Правда, если шагать все дальше, возрастание где-то сменится спадом. Про минимум говорят тогда, что он в точке х = а собственный. Значение абсолютного минимума получаем лишь тогда, когда это наименьшее значение функции для всей области определения.

5. "Периодическая"
   
6. "Ах, как томительны вечные спуски,
   

Как утомительны вечные взлеты!..

В каждой ложбине,

На каждой вершине -

Тщетной надеждой - мечта о привале,

Об остановке, о передышке.

Заключение.

Мы с вами живем в 21 веке, а еще в 5 веке до нашей эры древнегреческий историк Геродот писал, что египетские цари, разделив землю между египтянами, брали с каждого из них ежегодный налог, пропорциональный площади занимаемого участка. Конечно, ни египетские цари, ни землевладельцы, ни сам Геродот не произносили слова "f" , но ведь речь идет о том, что каждому значению S соответствовало некоторое значение налога.

Вы, моря шумного пучины,

Ты, неба вечного простор,

И ты, светил блестящий хор,

И вы, родной земли вершины,

Поля и пестрые цветы,

И с гор струящиеся воды -

Отдельно взятые черты

Всецельно дышащей природы!

Какая вас связала нить,

Одна другой светлей и краше?

Каким законом объяснить

Родство таинственное наше?

Как бы вы ответили на вопрос А.К. Толстого (таблица в начале урока)

Закон развития мира

"Признание всеобщей зависимости

предметов и явлений, человека и природы!"

И те, кто эту зависимость не видят , увы не хотят быть счастливыми.

Я хочу закончить урок цитатой из моей любимой книги.

« Пока не изучались переменные величины, пока не изучались связи и зависимости между ними, пока не изучались функции, пока в алгебре не было ее четвертого кита, в математике не изучалось движение, не отражалась настоящая диалектика, а значит, и польза от математики была ограниченной. Очень грубо говоря, до "поворотного пункта" математика была наукой для избранного круга любителей-мудрецов да для купцов и финансистов. Но лишь только она стала изучать переменные величины и функции, лишь только она научилась описывать процессы, описывать движение, как она стала необходима всем.»