Лгоритма его функционирования), устранения некорректности первичного описания и последовательного представления (при необходимости) описаний на различных языках

• Х описаний документов и пополнению сводного электронного каталога с целью устранения, 58kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Система Автоматизации Инженерного Труда cad computer Automation Design cam computer, 35.46kb.
• Проектирования это создание описания, необходимого для построения в заданных условиях, 258.57kb.
• История описания системных васкулитов, 320.25kb.
• История описания системных васкулитов, 320.23kb.
• Проект стандарт Форматы представления сведений из административной модели, 1588.72kb.
• Маркетинговые критерии оптимального функционирования фармацевтической компании, 241.01kb.
• Лекция № Библиографическое описание документа, 84.67kb.
• Ы (услуги) предприятия и его партнёров, и последующем их исполнении и контроле с помощью, 161.35kb.

13 При решении задач динамики используются либо уравнения силового равновесия системы - метод кинетостатики, либо уравнения энергетического равновесия - закон сохранения энергии. Для идеальной механической системы, в которой не потерь энергии и звенья абсолютно жесткие, этот закон можно применять в виде теоремы о изменении кинетической энергии. Согласно этой теореме работа всех внешних сил действующих на систему расходуется только на изменение ее кинетической энергии. При этом потенциальные силы - силы веса рассматриваются как внешние силы. f+m T = T - Tнач =  Аi , i=1 где T - изменение кинетической энергии системы, T - текущее значение кинетической энергии системы, Tнач - начальное значение кинетической энергии системы, n  Аi - суммарная работа внешних сил, действующих на систему. Рассмотрим сложную механическую систему (рис.6.1), состоящую из n подвижных звеньев из которых r - звеньев совершают вращательное движение, j - плоское, k - поступательное. Основная подвижность системы равна W=1. На систему действуют: f - внешних сил и m - внешних моментов. Движение этой системы определяется изменением одной независимой обобщенной координаты. Такую систему при решении задач динамики можно заменить более простой динамической моделью. Положение звена этой модели определяется обобщенной координатой, а динамические параметры заменяются: инерционные - суммарным приведенным моментом инерции Iпр , силовые - суммарным приведенным моментом Мпр . Эти параметры динамической модели рассчитываются по критериям подобия модели и объекта, которые определяются соответственно из равенства правых и левых частей уравнений изменения кинетической энергии для модели и объекта, т.е.где f+m  Аi - сумма работ всех внешних сил, действующих на систему, i=1 AМпр - работа суммарного приведенного момента, n  Ti - сумма кинетических энергий звеньев системы, i=1 Tм - кинетическая энергия динамической модели Определение параметров динамической модели машины (приведение сил и моментов). Рассмотрим изображенную на рис механическую систему и ее динамическую модель. Суммарная работа внешних сил: f _  _ m для механической системы Ac =   Fi  dSicos (Fi , dSi) +   Mi di , i=1 i=1 для модели Aм =  Мпрd1 . 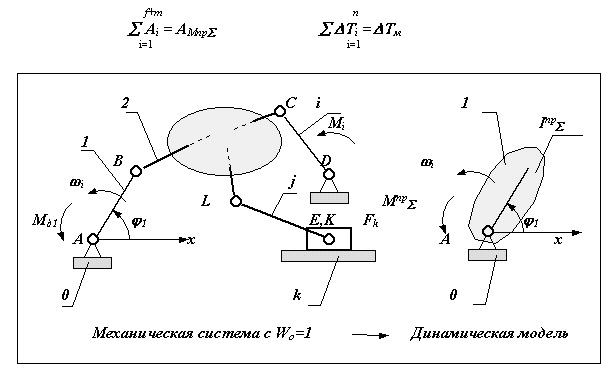Модель будет с энергетически эквивалентна рассматриваемой механической системе, если правые и левые части уравнений изменения кинетической энергии для модели и для системы будут соответственно равны. То есть выполняется условие Ac = Aм. Для того чтобы равенство выполнялось в течение всего диапазона изменения обобщенной координаты, необходимо обеспечить не равенство интегралов, а равенство подынтегральных выражений dAc =dAм . Подставляя в равенства, записанные ранее выражения для работ получим: f _  _ m Мпрd1 =  Fi  dSicos (Fi , dSi) +  Mi di . i=1 i=1 Из уравнения для правых частей получаем формулу для определения приведенного суммарного момента динамической модели f _  _ m Мпр =  Fi (dSi /d1) cos (Fi , dSi) +  Mi(di/ d1). i=1 i=1 f _  _ m Мпр =  Fi VqSi  cos (Fi , dSi) +  Mi qi.	14 Машинный агрегат - развитое машинное устройство , состоящее из двигателя, передаточных механизмов и рабочей машины и в некоторых случаях контрольно-управляющих и счетно-решающих устройств. Рассмотрим сложную механическую систему (рис.6.1), состоящую из n подвижных звеньев из которых r - звеньев совершают вращательное движение, j - плоское, k - поступательное. Основная подвижность системы равна W=1. На систему действуют: f - внешних сил и m - внешних моментов. Движение этой системы определяется изменением одной независимой обобщенной координаты. Такую систему при решении задач динамики можно заменить более простой динамической моделью. Положение звена этой модели определяется обобщенной координатой, а динамические параметры заменяются: инерционные - суммарным приведенным моментом инерции Iпр , силовые - суммарным приведенным моментом Мпр . Эти параметры динамической модели рассчитываются по критериям подобия модели и объекта, которые определяются соответственно из равенства правых и левых частей уравнений изменения кинетической энергии для модели и объекта, т.е.  Аi - сумма работ всех внешних сил, действующих на систему, i=1 AМпр - работа суммарного приведенного момента, n  Ti - сумма кинетических энергий звеньев системы, i=1 Tм - кинетическая энергия динамической модели Определение параметров динамической модели машины (приведение сил и масс). Рассмотрим изображенную на рис механическую систему и ее динамическую модель. Запишем для них уравнение изменения кинетической энергии. Кинетическая энергия: r+k r+j для механической системы Тс =  mi VSi2/2 +  Isi  i2/2 , i=1 i=1для модели Tм = Iпр21/2 ; Модель будет с энергетически эквивалентна рассматриваемой механической системе, если правые и левые части уравнений изменения кинетической энергии для модели и для системы будут соответственно равны. То есть частей выполняется условие Тс = Тм. Подставляя в равенства, записанные ранее выражения для кинетических энергий получим: для левых частей r+k r+j Iпр21/2 =  mi VSi2/2 +  Isi  i2/2 , i=1 i=1 Из уравнения для левых частей получаем формулу для определения приведенного суммарного момента инерции динамической модели r+k r+j Iпр=  mi (VSi/1)2 +  Isi  (i/1)2 , i=1 i=1 r+k r+j Iпр=  mi (VqSi)2 +  Isi  (qi)2 . i=1 i=1	18 Механические характеристики машин. Механической характеристикой машины называется зависимость силы или момента на выходном валу или рабочем органе машины от скорости или перемещения точки или звена ее приложения. Рассмотрим примеры механических характеристик различных машин. Двигатели внутреннего сгорания (ДВС): четырехтактный ДВС Индикаторная диаграмма - графическое изображение зависимости давления в цилиндре поршневой машины от хода поршня. двухтактный ДВС Электродвигатели асинхронный электродвигатель переменного тока 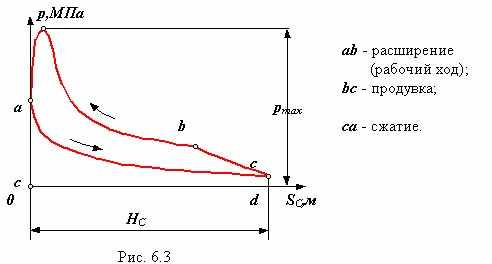На диаграмме: Мдп - пусковой момент; Мдн - номинальный крутящий момент; Мдк или Мдmax - критический или максимальный момент; дн - номинальная круговая частота вращения вала двигателя; дхх или дс - частота вращения вала двигателя холостого хода или синхронная. Уравнение статической характеристики асинхронного электродвигателя на линеаризованном участке устойчивой части Мд = b1 + k1д ,где Мд - движущий момент на валу двигателя, д - круговая частота вала двигателя , b1 = Мдн  д /(дс - дн ) , k1 = - Мдн / (дс - дн ). Статическая характеристика асинхронного двигателя, выражающая зависимость нагрузки от скольжения, определяется формулой Клосса Мд =2Мдк(S/Sк + Sк/S ), где S = 1 - д /дс , Sк = 1 - дк /дс , д >=дс . 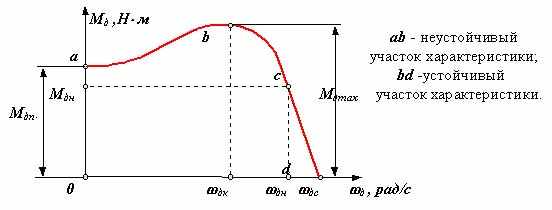двигатель постоянного тока с независимым возбуждением Уравнение статической характеристики для двигателя постоянного тока с независимым возбуждением Мд = Mдн + k (дн - д ) , где k = Мдн /(дхх - дн ). В электрических параметрах характеристика записывается в следующем виде Мд = kM  (Uя - k д)/ Rя , где kM = Mдн/Iян - коэффициент момента, k = (Uян - Rя Iян ) / дн - коэффициент противоэлектродвижущей силы, Uя - напряжение в цепи якоря, Rя - сопротивление цепи якоря 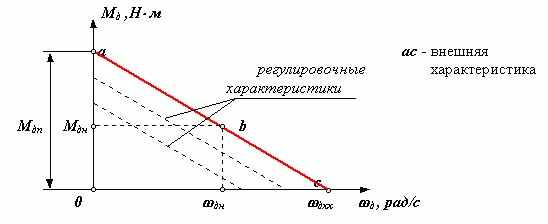Рабочие машины поршневой насос поршневой компрессор Линии bc и ad - линии сжатия и расширения газа (воздуха) определяются параметрами газа (объемом, давлением и температурой) и в общем виде описываются уравнением политропы p Vn = const , где n - показатель политропы ( 1 n  0 ). Механические характеристики определяют внешние силы и моменты, действующие на входные и выходные звенья, рассматриваемой механической системы со стороны взаимодействующих с ней внешних систем и окружающей среды. Характеристики определяются экспериментально, по результатам экспериментов получают регрессионные эмпирические модели, которые в дальнейшем используются при проведении динамических расчетов машин и механизмов.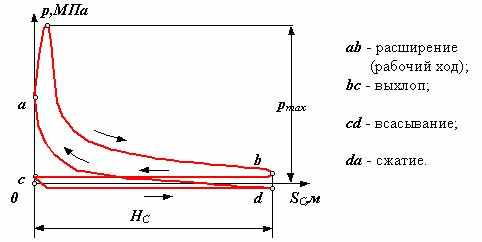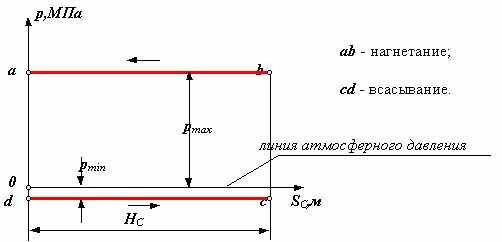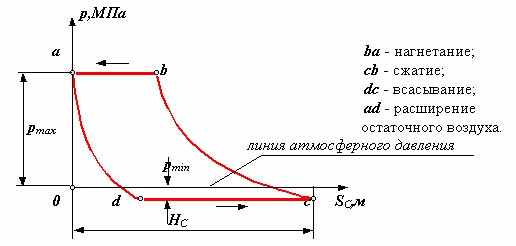
19 Режим движения «пуск - останов». С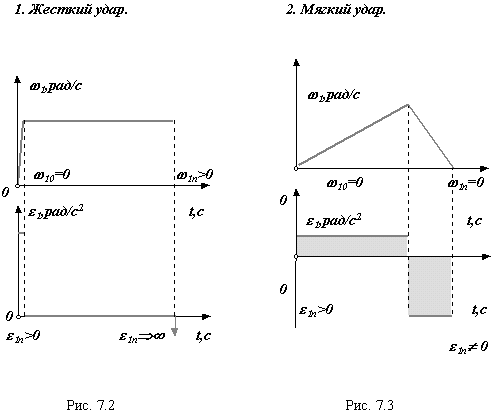уществует большое количество машин и механизмов: гидроподъемники, манипуляторы, механизмы управления метательными аппаратами, механизмы шасси, механизмы автоматических дверей и многие другие, исполнительное звено которых перемещается из начального положения в конечное. При этом в начале и в конце цикла движения исполнительное звено неподвижно. Такой режим движения механизма называется режимом «пуск-останов». Механизм начинает движение из состояния покоя, в конце цикла выходное звено механизма должно остановиться и зафиксироваться в заданном положении. Возможны три варианта остановки выходного звена: остановка с жестким ударом (рис.7.2) 1n  0, 1n  ; остановка с мягким ударом (рис. 7.3 ) 1n = 0, 1n  0 . Для динамической модели в конечном положении __________________ 1n =  2  (An + Тнач)/ Iпрn, Если Тнач = 0, Iпр n 0, то Аn = 0. безударная остановка или остановка с удержанием в конечном положении (рис. 7.4) 1n = 0, 1n = 0 . В этом случае к рассмотренному выше условию 1n = 0 , добавляется условие 1n = 0. Для динамической модели в конечном положении 1n = d1n/dt = М прn / Iпрn - 1n2/(2 Iпрn)  (d Iпрn /d1), Если 1n = 0, Iпр  0, то 1n = 0 при М прn = 0. Таким образом при остановке с мягким ударом необходимо выполнить условие 1n = 0  Аn = 0; при безударной установке и фиксации объекта в конечном положении нужно выполнить одновременно два условия 1n = 0  Аn = 0; 1n = 0  М прn = 0. 1. Жесткий удар. 2. Мягкий удар. 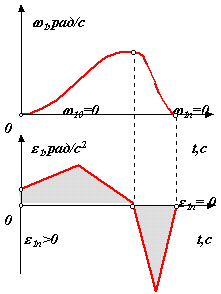Безударная остановка объекта в конечном положении с фиксацией. Для того, чтобы выполнить условия начала движения и остановки выходного звена в конечном положении необходимо соответствующим образом выбрать закон изменения движущих или управляющих сил.	21 Алгоритм решения прямой задачи динамики при неустановившемся режиме. 1. Выбор динамической модели и определение ее параметров. 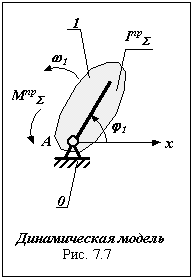В качестве динамической модели принимаем звено 1, совершающее вращательное движение вокруг точки А с круговой частотой w1 , положение которого определяется обобщенной координатой j1 . Параметры динамической модели: суммарный приведенный момент инерции звеньев механизма Iпрå и суммарный приведенный момент, действующих на него внешних сил, Mпрå определяются в следующей последовательности: 1.1. Определение кинематических передаточных функций для звеньев механизма u21 = u31 , центров масс VqS1 , VqS2 и VqS3 и точки приложения движущей силы VqD . Для определения этих функций воспользуемся методом проекций векторного контура механизма . 1.2. Определение движущей силы по условиям в начале и в конце цикла. 1.3. Определение приведенного суммарного момента. 1.4. Определение суммарного приведенного момента инерции. 2. Определение суммарной работы внешних сил. Суммарную работу внешних сил получим интегрированием суммарного приведенного момента Мпр по обобщенной координате d1 ./6 Aм =  Мпр  d1 0 3. Определение угловой скорости звена приведения. __________________ w1i = Ö 2× (AМпрåi + Tнач)/ Iпрåi 4. Определение времени цикла. Время цикла определяется по диаграмме t = f (1). Для построения этой диаграммы проведем интегрирование диаграммы угловой скорости ./6 d1 / dt = 1  dt = d1 / 1 , t =  d1 / 1 . 0 6. Определение углового ускорения звена приведения Для расчета углового ускорения звена приведения 1 = f(1 ) можно воспользоваться двумя различными зависимостями: а). 1 = d1 /dt = d1/d1  d1/dt = 1  d1/d1 , б). 1 = d1/dt = М пр/ Iпр - 12/(2 Iпр)  (d Iпр /d1). Применение первой формулы приводит к большим погрешностям, так как она основывается на использовании одной из конечных зависимостей расчета 1 = f (1 ). Кроме того, в точках с нулевыми значениями 1 расчет по этой формуле дает неверный результат 1 = 0. Поэтому проведем расчет зависимости 1 = f(1 ) по второй формуле.	22 Прямая задача динамики машины: определение закона движения при неустановившемся (переходном) режиме. В отличие от установившегося режима движения режимы разгона и торможения называются неустановившимися. К этому режиму относят и режим движения «пуск-останов». Прямая задача динамики: определение закона движения машины при заданных внешних силовых воздействиях ( как сил и моментов сопротивления, так и движущих или управляющих сил ). Эта задача относится к задачам анализа, при которых параметры механизмов заданы, либо могут быть определены на предварительных этапах расчета. Алгоритм решения прямой задачи динамики при неустановившемся режиме. Постановка задачи . Дано: Кинематическая схема механизма и его размеры массы и моменты инерции ____________________________________________ Определить: 1 = f(1 ), t = f(1 ), 1 = f( t ), 1 = f(1 ). 1. Выбор динамической модели и определение ее параметров. В качестве динамической модели принимаем звено 1, совершающее вращательное движение вокруг точки А с круговой частотой 1 , положение которого определяется обобщенной координатой 1 . Параметры динамической модели: суммарный приведенный момент инерции звеньев механизма Iпр и суммарный приведенный момент, действующих на него внешних сил, Mпр определяются в следующей последовательности: 1.1. Определение кинематических передаточных функций для звеньев механизма, центров масс и точки приложения движущей силы. 1.2. Определение движущей силы по условиям в начале и в конце цикла. Fд = f(S) 1.3. Определение приведенного суммарного момента . определение приведенного суммарного момента сил сопротивления Мпр = f(1). 1.4. Определение суммарного приведенного момента инерции Iпр =f(1). 2. Определение суммарной работы внешних сил. A=f(1). 3. Определение угловой скорости звена приведения Определение закона движения звена приведения в виде диаграммы изменения угловой скорости в функции обобщенной координаты 1= f(1) проводится по формуле _______________ 1i =  2 (AМпрi + Tнач)/ Iпрi , Tнач =0 4. Определение времени цикла. Время цикла определяется по диаграмме t = f (1). Для построения этой диаграммы проведем интегрирование диаграммы угловой скорости ./6 d1 / dt = 1  dt = d1 / 1 , t =  d1 / 1 . 0 5.Определение углового ускорения звена приведения Для расчета углового ускорения звена расчета углового ускорения звена приведения 1 = f(1 ) можно воспользоваться двумя различными зависимостями: а). 1 = d1 /dt = d1/d1  d1/dt = 1  d1/d1 , б). 1 = d1/dt = М пр/ Iпр - 12/(2 Iпр)  (d Iпр /d1). Применение первой формулы приводит к большим погрешностям, так как она основывается на использовании одной из конечных зависимостей расчета 1 = f (1 ). Кроме того, в точках с нулевыми значениями 1 расчет по этой формуле дает неверный результат 1 = 0. Поэтому проведят расчет зависимости 1 = f(1 ) по второй формуле.