Лгоритма его функционирования), устранения некорректности первичного описания и последовательного представления (при необходимости) описаний на различных языках
| Вид материала | Документы |
- Х описаний документов и пополнению сводного электронного каталога с целью устранения, 58kb.
- Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
- Система Автоматизации Инженерного Труда cad computer Automation Design cam computer, 35.46kb.
- Проектирования это создание описания, необходимого для построения в заданных условиях, 258.57kb.
- История описания системных васкулитов, 320.25kb.
- История описания системных васкулитов, 320.23kb.
- Проект стандарт Форматы представления сведений из административной модели, 1588.72kb.
- Маркетинговые критерии оптимального функционирования фармацевтической компании, 241.01kb.
- Лекция № Библиографическое описание документа, 84.67kb.
- Ы (услуги) предприятия и его партнёров, и последующем их исполнении и контроле с помощью, 161.35kb.
| 29 Приведение задачи синтеза механизма по ФП к задаче синтеза по трем положениям . По исходным данным ( Dg3 , g30 и u31 ) построим график заданной ФП. Так как u31 = const, то u31 = dg3 / dj1 = Dg3 / Dj1 , откуда определим перемещение входного звена Dj1, соответствующее рабочему перемещению выходного звена Dg3 . Заданная ФП будет диагональю прямоугольника abcd (при u31 > 0 - диагональ ас, при u31 < 0 - bd ). Положим u31 < 0, тогда начальная координата g30 больше конечной g3n и соответствует ординате т. b. Если u31 > 0 , то g3n > g30 и g30 соответствует ордината т. а . Для описания рабочего участка ФП разобьем отрезок ac на три равные части (точки e, f, q), выбрав первую точку случайным образом, и определим ординаты этих точек g31 , g32 и g33 , а также приращения абсциссы Dj2 и Dj3 . Углы g31 , g32 и g33 определяют некоторые три положения выходного звена на рабочем участке, а приращения углов Dj2 и Dj3 - углы поворота входного звена при переходе звена 3 соответственно из положения 1 (т. е) в 2 (т. f) и из 1 в 3 (т. q) . Эти величины в совокупности с размерами l3 и l4 (или e) позволяют свести задачу синтеза механизма по заданной ФП к известной задаче синтеза механизма по трем положениям. Решение задачи синтеза механизма по трем положениям. Г 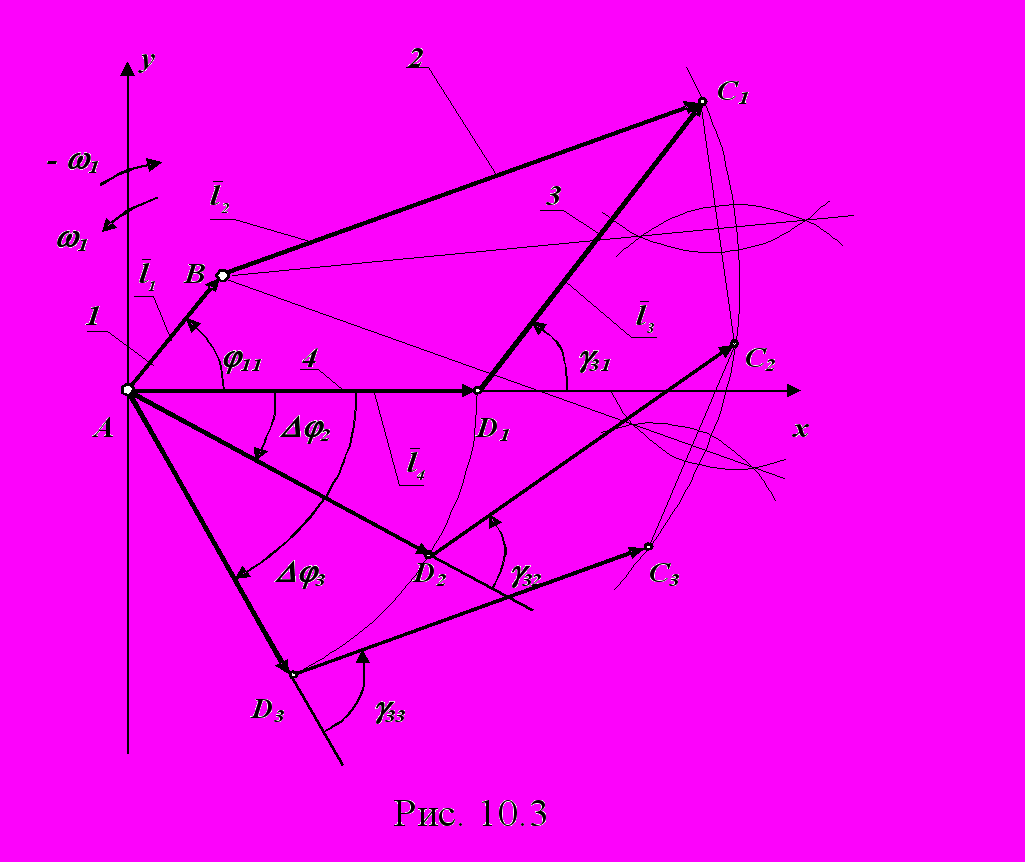 рафический метод решения. Рассмотрим движение механизма в неподвижной системе координат X A Y . Относительно этой системы звенья движутся с исходными угловыми скоростями, значения которых приведены во второй строке. рафический метод решения. Рассмотрим движение механизма в неподвижной системе координат X A Y . Относительно этой системы звенья движутся с исходными угловыми скоростями, значения которых приведены во второй строке.
Для того, чтобы звено 1 (вектор l1) в системе координат XAY стало неподвижным, необходимо сообщить всем звеньям механизма дополнительное вращение со скоростью - w1 . При этом звено 4 станет подвижным и будет вращаться относительно точки А со скоростью - w1 . В системе координат XAY в обращенном движении изобразим в трех положениях векторную сумму `l3 + `l4 , определяющую положения центра шарнира Ci. Отложим по оси x вектор `l4. Из конца этого вектора вектора под углом g31 к его направлению отложим вектор `l3 и получим положение точки C1 . Повернем вектор `l4 в направлении - w1 на угол Dj2 . Из точки D под углом g32 к нему проведем вектор `l3 и найдем положение точки C2 . Сделав аналогичные построения для третьего положения векторной суммы с угловыми координатами Dj3 и g33 , определим положение точки C3. Шарнир В образован звеньями 1 и 2 и в обращенном движении неподвижен. Шарнир С соединен с шарниром В звеном 2, поэтому точки C i лежат на окружности радиуса l2 c центром в точке В. Чтобы графически определить центр В окружности, проходящей через три заданных точки, необходимо провести две прямые: С1С2 и С2С3 . Затем через их середины провести перпендикуляры , точка пересечения которых будет искомой точкой В . Указанные построения выполняют в натуральную величину ( m l = 1 мм / мм ). Отрезки на чертеже соответствуют размерам звеньев l1 = AB / m l , l2 = BC1 / m l , а угол Ð ВAD = j11 - начальной угловой координате звена 1. Основные преимущества графического метода - простота и наглядность. Недостатки - невысокая точность, особенно, если угол между перпендикулярами небольшой. Аналитический метод решения. Координаты точек C i (i=1,2,3) определяются проекциями векторной суммы `l4+`l3 (или`S3i+`e ) на координатные оси: xci = ai cosDj i + b cos(g3 i - D j i ); yci = -ai sinDj i + b sin(g3 i -Dj i ). Где ai = l4 , b = l3 , Dj1 = j1 i -j11 - для шарнирного четырехзвенника; ai = S3 i , b = e, Dj = j1 i - j1 1 , g31 = 90 ° - для кривошипно-ползунного механизма. Координаты (xB, yB) точки В окружности, проходящей через точки С i с координатами (xci ,yci ), определим по системе трех уравнений с тремя неизвестными xB , yB и l2 : ( xc i - xB )2 + ( yc i - yB )2 = l22 . откуда l2 = 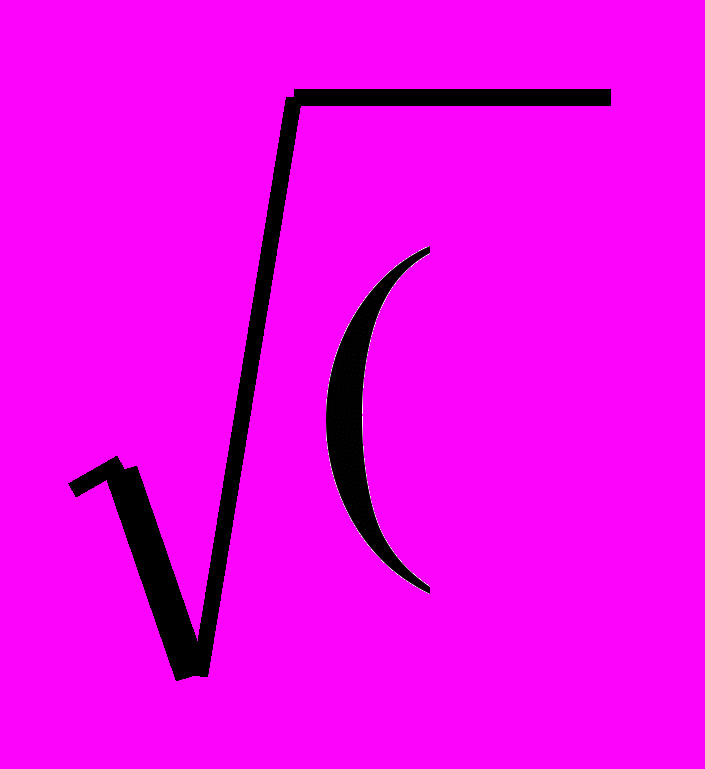 xc1 - xB )2 + ( yc1 - yB)2 xc1 - xB )2 + ( yc1 - yB)2 l1 = 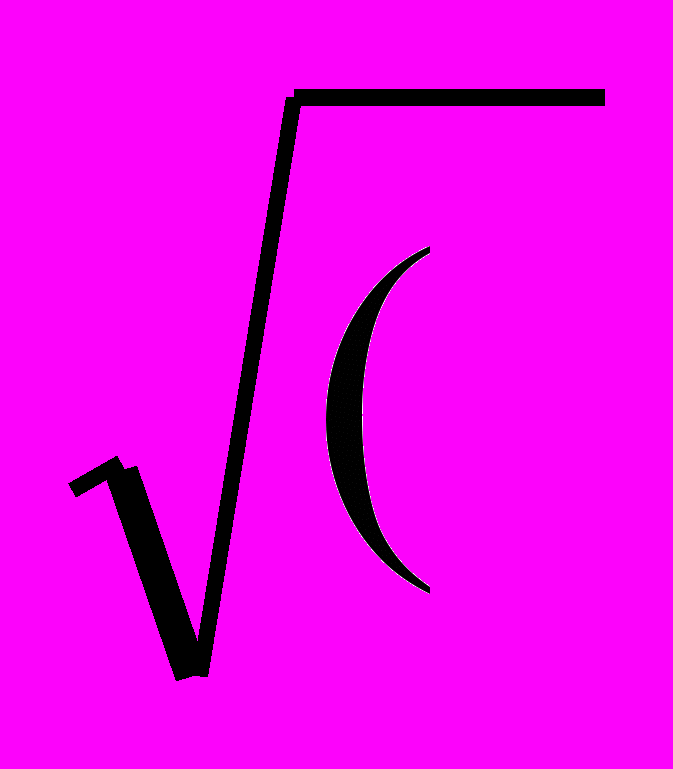 x2B + y2B ) , x2B + y2B ) , j11 = arcsin ½ yB / l1 ½ , где при j11 = j¢11 xB > 0 , yB > 0 ; при j11 = 180° - j¢11 xB < 0 , yB > 0 ; при j11 =180° + j¢11 xB < 0 , yB < 0 ; при j11 = 360° - j¢11 xB > 0 , yB < 0 ; j¢11 - главное значение угла. Для синтезированного механизма по правилу Грасгофа определим число кривошипов: если L1 + L4 < L2 + L3 и L1 = l4 , то механизм двухкривошипный; если L1 + L4 < L2 + L3 и L1 = l1 или L1 = l3 , то механизм кривошипно-коромысловый, в противном случае, механизм двухкоромысловый. Длины звеньев механизма Li рассортированы по условию: L1 < L2 < L3 < L4 . Вращающееся звено механизма называют кривошипом, если оно может поворачиваться на угол 2p и более, или коромыслом, если угол его поворота меньше2p . При проектировании кривошипно-ползунного механизма проверяют условие существования кривошипа l1 < l2 - | e | .Если это неравенство не выполняется, то механизм будет коромыслово-ползунным. | 30 Оптимальный синтез рычажных механизмов. Задача оптимального проектирования - это экономико-математическая задача, содержащая критерий оптимальности и ограничения и направленная на поиск лучшего в определенных условиях (т.е оптимального) значения показателя. Оптимизация - отыскание такого решения рассматриваемой задачи, которое дает экстремальное (минимальное или максимальное) значение некоторой функции, называемой целевой. При оптимальном метрическом синтезе механизма необходимо определить такое сочетание его размеров (внутренние параметры), которое наилучшим образом удовлетворяет требуемым эксплуатационным и качественным показателям (критерии оптимизации и ограничивающие условия). При метрическом синтезе в качестве качественных показателей обычно используются: габариты механизма, точность обеспечения заданных положений или закона движения (функции положения или передаточной функции), условия передачи сил в КП (углы давления в КП) и другие показатели. Механизм при оптимальном проектировании характеризуется двумя n-мерными векторами: параметров и качественных показателей. На значения как параметров, так и качественных показателей могут быть наложены некоторые ограничения в виде равенств или неравенств. Ограничения могут быть:
О 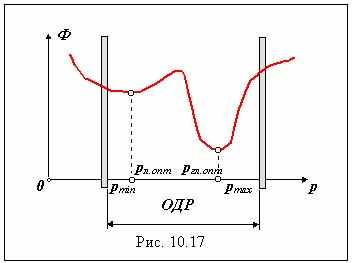 граничения формируют область допустимых значений параметров, в пределах которой осуществляется поиск оптимального решения. В пределах этой области могут существовать локальные и глобальный оптимум целевой функции. Целевая функция может быть одномерной или многомерной. При многомерной оптимизации необходимо формирование сложной целевой функции, учитывающей вес каждого из качественных показателей, например, аддитивной граничения формируют область допустимых значений параметров, в пределах которой осуществляется поиск оптимального решения. В пределах этой области могут существовать локальные и глобальный оптимум целевой функции. Целевая функция может быть одномерной или многомерной. При многомерной оптимизации необходимо формирование сложной целевой функции, учитывающей вес каждого из качественных показателей, например, аддитивной Ф ( G , d , J , ... ) = k1× G + k2 × d + k3 × J + ... или мультипликативной функции Ф ( G , d , J , ... ) = G k1× d k2 × J k3 × ... где Ф ( G , d , J , ... ) - целевая функция, G - габариты механизма, d - точность механизма, J - углы давления в КП механизма, ki - весовые коэффициенты при качественных показателях. На рис. 10.17 представлена целевая функция при однопараметрической оптимизации ( р - параметр оптимизируемой системы ). Ограничения по параметру рmin и pmax определяют область допустимых решений (ОДР), в пределах которой проводится поиск оптимального решения. В нашем примере в этой области целевая функция имеет два минимума: локальный при рл.опт и глобальный при ргл.опт . Задача считается решенной после определения глобального экстремума функции. Методы решения задач оптимизации весьма разнообразны и являются предметом изучения в таких учебных дисциплинах как вычислительная математика, математическое программирование, САПР . | 32,33 Виброзащита в машинах и механизмах. Как отмечалось ранее, при движении механической системы под действием внешних сил в ней возникают механические колебания или вибрации. Эти вибрации оказывают влияние на функционирование механизма и часто ухудшают его эксплуатационные характеристики: снижают точность, уменьшают КПД и долговечность машины, увеличивают нагрев деталей, снижают их прочность, оказывают вредное воздействие на человека-оператора. Для снижения влияния вибраций используют различные методы борьбы с вибрацией. С одной стороны при проектировании машины принимают меры для снижения ее виброактивности (уравновешивание и балансировка механизмов), с другой - предусматриваются средства защиты как машины от вибраций, исходящих от других машин (для рассматриваемой машины от среды), так среды и операторов от вибраций данной машины. Методы виброзащиты. Существующие виброзащитные устройства по методу снижения уровня вибраций делятся на:
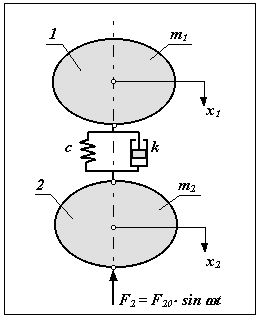 Подрессоривание или виброизоляция. Подрессоривание или виброизоляция.При виброизоляции между рассматриваемыми звеньями устанавливают линейный или нелинейный виброизолятор, который обычно состоит из упругого и демпфирующего элементов В этой механической системе x2 ¹ x1 ( предположим, что x2 > x1 ) и Dx = x2 - x1 , тогда кинетическая энергия системы · · T = m1× x12 / 2 + m2× x22 / 2, а потенциальная U = c × Dx2 / 2. Т 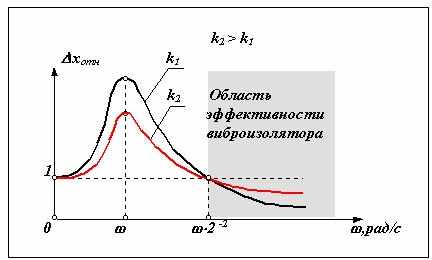 о есть в системе с виброизолятором только часть работы внешней силы расходуется на изменение кинетической энергии. Часть этой работы переходит в потенциальную энергию упругого элемента и часть рассеивается демпфером (переходит в тепло и рассеивается в окружающей среде). о есть в системе с виброизолятором только часть работы внешней силы расходуется на изменение кинетической энергии. Часть этой работы переходит в потенциальную энергию упругого элемента и часть рассеивается демпфером (переходит в тепло и рассеивается в окружающей среде).Уравнения движения ·· | ||||||||||||||||||||
