Лгоритма его функционирования), устранения некорректности первичного описания и последовательного представления (при необходимости) описаний на различных языках

• Х описаний документов и пополнению сводного электронного каталога с целью устранения, 58kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Система Автоматизации Инженерного Труда cad computer Automation Design cam computer, 35.46kb.
• Проектирования это создание описания, необходимого для построения в заданных условиях, 258.57kb.
• История описания системных васкулитов, 320.25kb.
• История описания системных васкулитов, 320.23kb.
• Проект стандарт Форматы представления сведений из административной модели, 1588.72kb.
• Маркетинговые критерии оптимального функционирования фармацевтической компании, 241.01kb.
• Лекция № Библиографическое описание документа, 84.67kb.
• Ы (услуги) предприятия и его партнёров, и последующем их исполнении и контроле с помощью, 161.35kb.

72 Понятие о КПД механической системы. Коэффициентом полезного действия или КПД механической системы называют отношение работы сил полезного сопротивления к работе движущих сил за цикл ( или целое число циклов ) установившегося режима работы. КПД механизма характеризует его эффективность при преобразовании энергии, определяет соотношение полученной на выходе полезной энергии и энергетических потерь в механизме на трение, перемешивание масла, вентиляцию, деформацию звеньев и др. Величину КПД можно рассчитать по следующей зависимости: 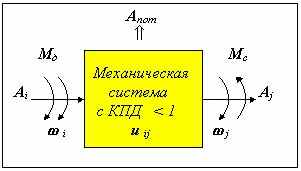h = | Aj /Ai | = | Аi - Aпот | / | Ai | , h = 1 - | Aпот/ | Ai | = 1 - y , где Ai - работа движущих сил, Aj - работа сил полезного сопротивления, h - коэффициент полезного действия, y - коэффициент потерь. Работа движущих сил за цикл jin Аi = ò Мд × dji » Мдср × (jin - ji0 ) » Мдср × Dji , ji0 работа сил полезного сопротивления за цикл jjn Аj = ò Мс × djj » Мcср × (jjn - jj0 ) » Мcср × Djj , jj0 где Мдср и Мcср - среднеинтегральные значения движущего момента и момента сил сопротивления, jin ,jjn и ji0 , jj0 - значения угловых координат звеньев i и j ,соответственно в начале и в конце цикла. Подставим эти выражения в формулу для КПД и получим h = | Aj /Ai | = | Мcср × Djj | / | Мдср × Dji | = | Мcср × | / | Мдср | , где uji - передаточное отношение механизма. КПД механической системы при последовательном и параллельном соединении механизмов. Последовательное соединение при последовательном соединении (рис. 9.11) весь поток механической энергии проходит последовательно через каждый из механизмов П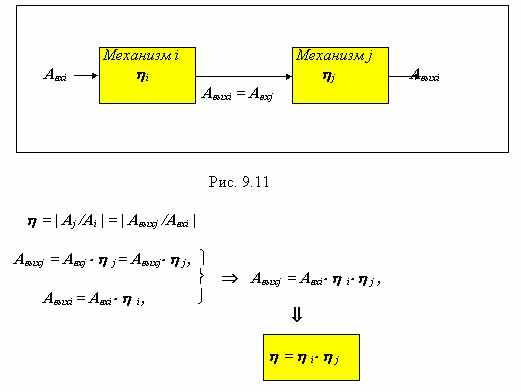араллельное соединение при параллельном соединении механизмов i и j (рис. 9.12) поток механической энергии делится на две части: часть проходящую через механизм i обозначим µ, а часть проходящую через механизм j Þ b, причем µ +b = 1.

73 Промышленные роботы и манипуляторы. Промышленный робот – автоматическая машина, состоящая из манипулятора и устройства программного управления его движением, предназначенная для замены человека при выполнении основных и вспомогательных операций в производственных процессах. Манипулятор – совокупность пространственного рычажного механизма и системы приводов, осуществляющая под управлением программируемого автоматического устройства или человека-оператора действия (манипуляции), аналогичные действиям руки человека. Назначение и область применения. Промышленные роботы предназначены для замены человека при выполнении основных и вспомогательных технологических операций в процессе промышленного производства. При этом решается важная социальная задача - освобождения человека от работ, связанных с опасностями для здоровья или с тяжелым физическим трудом, а также от простых монотонных операций, не требующих высокой квалификации. Гибкие автоматизированные производства, создаваемые на базе промышленных роботов, позволяют решать задачи автоматизации на предприятиях с широкой номенклатурой продукции при мелкосерийном и штучном производстве. Копирующие манипуляторы, управляемые человеком-оператором, необходимы при выполнении различных работ с радиоактивными материалами. Кроме того, эти устройства незаменимы при выполнении работ в космосе, под водой, в химически активных средах. Таким образом, промышленные роботы и копирующие манипуляторы являются важными составными частями современного промышленного производства. Классификация промышленных роботов. Промышленные роботы классифицируются по следующим признакам: по характеру выполняемых технологических операций основные; вспомогательные; универсальные; по виду производства литейные; сварочные; кузнечно-прессовые; для механической обработки; сборочные; окрасочные; транспортно-складские; по системе координат руки манипулятора прямоугольная; цилиндрическая; сферическая; сферическая угловая (ангулярная); другие; по числу подвижностей манипулятора; по грузоподъемности сверхлегкие (до 10 Н); легкие (до 100 Н); средние (до 2000 Н); тяжелые (до 10000 Н); сверхтяжелые (свыше 10000 Н); по типу силового привода электромеханический; пневматический; гидравлический; комбинированный; по подвижности основания мобильные; стационарные; по виду программы с жесткой программой; перепрограммируемые; адаптивные; с элементами искусственного интеллекта; по характеру программирования позиционное; контурное; комбинированное. Рабочее пространство манипулятора - часть пространства, ограниченная поверхностями огибающими к множеству возможных положений его звеньев. Зона обслуживания манипулятора - часть пространства соответствующая множеству возможных положений центра схвата манипулятора. Зона обслуживания является важной характеристикой манипулятора. Она определяется структурой и системой координат руки манипулятора, а также конструктивными ограничениями наложенными относительные перемещения звеньев в КП. Подвижность манипулятора W - число независимых обобщенных координат однозначно определяющее положение схвата в пространстве. 5 W= 6× n - å (6 - i )× pi i=1 или для незамкнутых кинематических цепей. 5 W = å i× pi . i=1 Маневренность манипулятора М - подвижность манипулятора при зафиксированном (неподвижном) схвате. М = W - 6 . В манипуляторе можно выделить два участка кинематической цепи с различными функциями: механизм руки и механизм кисти. Под «рукой» понимают ту часть манипулятора, которая обеспечивает перемещение центра схвата – точки М ( региональные движения схвата); под «кистью» – те звенья и пары, которые обеспечивают ориентацию схвата (локальные движения схвата).

74 Волновые передачи. Назначение и области применения. Волновой передачей называется зубчатый или фрикционный механизм, предназначенный для передачи и преобразования движения (обычно вращательного), в котором движение преобразуется за счет волновой деформации венца гибкого колеса специальным звеном (узлом) – генератором волн. Основными элементами дифференциального волнового механизма являются: входной или быстроходный вал с генератором волн, гибкое колесо с муфтой, соединяющей его с первым тихоходным валом, жесткое колесо, соединенное со вторым тихоходным валом, корпус. 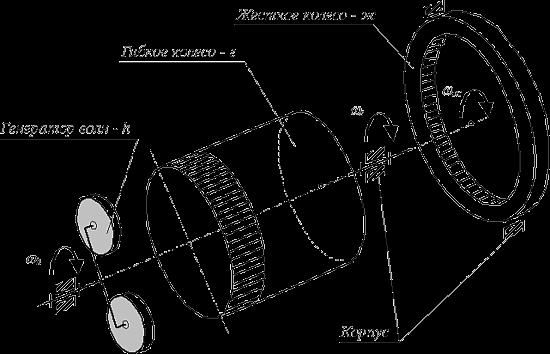Преимущества и недостатки волновых передач. Преимущества: Возможность реализации в одной ступени при двухволновом генераторе волн больших передаточных отношений в диапазоне от 40 до 300. Высокая нагрузочная способность при относительно малых габаритах и массе. Малый мертвый ход и высокая кинематическая точность. Возможность передачи движения через герметичную перегородку. Малый приведенный к входному валу момент инерции (для механизмов с дисковыми генераторами волн). Недостатки: Меньшая приведенная к выходному валу крутильная жесткость. Сложная технология изготовления гибких зубчатых колес. Кинематика волнового механизма. 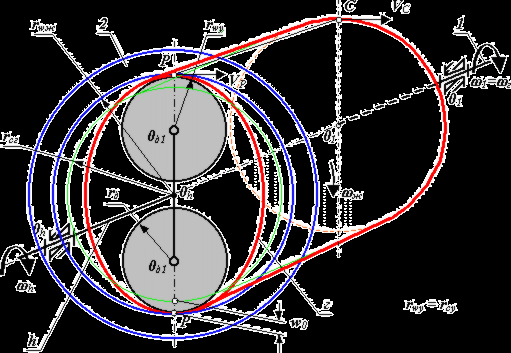rwу - радиус начальной окружности условного колеса; rwж - радиус начальной окружности жесткого колеса; rд - радиус деформирующего диска; rсг - радиус срединной окружности гибкого колеса; rсу - радиус срединной окружности условного колеса; w0 - радиальная деформация гибкого колеса. Рассмотрим движение звеньев дифференциального волнового механизма относительно генератора волн. Тогда угловые скорости звеньев изменятся следующим образом: Движение механизма Звено г Звено ж Звено h Звен0 Отн. стойки wг wж wh w0=0 Отн. генератора волн w*г=wг-wh w*ж=wж-wh wh-wh=0 -wh В движении звеньев относительно генератора волн скорости звеньев равны угловым скоростям в движении относительно стойки минус угловая скорость генератора. Скорость точки жесткого колеса, совпадающей с полюсом зацепления VPж = (wж-wh)×rwж , а скорость точки, совпадающей с полюсом на гибком колесе VPг = (wг-wh)×rwг . В полюсе зацепления нет скольжения и VPж = VPг , а так как срединную поверхность оболочки считаем нерастяжимой то VPг = VС . Тогда для движения относительно генератора волн VPж = (wж-wh)×rwж , VС = (wг-wh)×rwг , VPж = VС Þ (wж-wh)×rwж = (wг-wh)×rwг , (wж-wh)/ (wг-wh) = rwг / rwж = zг / zж , zж × wж + (zг – zж) × wh - zг× wг = 0. Для волнового зубчатого редуктора [ 1 ]: при заторможенном жестком колесе wж= 0 uhгж = wh / wг = - zг / (zж – zг); при заторможенном гибком колесе wг= 0 uhжг = wh / wж = zж / (zж – zг). Расчет геометрии волнового зубчатого зацепления. В расчете геометрии волнового зацепления существует два основных подхода. В первом методе исследуется относительное движение зубьев и, на основе этого, разрабатываются рекомендации по выбору геометрических параметров зацепления. Второй метод основан на использовании расчетного внутреннего зацепления жесткого колеса с условным расчетным колесом. Это колесо вписывается в деформированное гибкое колесо на участке возможного зацепления. Преимуществом первого метода можно считать относительную универсальность, которая позволяет в расчете геометрии учитывать деформации как гибкого, так и жесткого колеса под нагрузкой. Однако разработать рекомендации даже для небольшого количества конструкций ВЗП затруднительно. Второй метод позволяет использовать для расчета геометрии стандартный асчет внутреннего эвольвентного зацепления для пары колес zж и zу