Лгоритма его функционирования), устранения некорректности первичного описания и последовательного представления (при необходимости) описаний на различных языках
| Вид материала | Документы |
| Линия станочного зацепления Смещение исходного производящего контура Уравнительное смещение Окружность граничных точек |
- Х описаний документов и пополнению сводного электронного каталога с целью устранения, 58kb.
- Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
- Система Автоматизации Инженерного Труда cad computer Automation Design cam computer, 35.46kb.
- Проектирования это создание описания, необходимого для построения в заданных условиях, 258.57kb.
- История описания системных васкулитов, 320.25kb.
- История описания системных васкулитов, 320.23kb.
- Проект стандарт Форматы представления сведений из административной модели, 1588.72kb.
- Маркетинговые критерии оптимального функционирования фармацевтической компании, 241.01kb.
- Лекция № Библиографическое описание документа, 84.67kb.
- Ы (услуги) предприятия и его партнёров, и последующем их исполнении и контроле с помощью, 161.35kb.
Два зубчатых колеса с одинаковым модулем и с числами зубьев соответствующими заданному передаточному отношению образуют зубчатую передачу или простейший зубчатый механизм. В этом трехзвенном механизме зубчатые колеса образуют между собой высшую пару, а со стойкой низшие пары. Зубчатая передача, кроме параметров образующих ее колес, имеет и собственные параметры: угол зацепления aw, межосевое расстояние aw, воспринимаемое смещение y×m и уравнительное смещение Dy×m . Передаточное отношение механизма u12, числа зубьев колес z1 и z2, начальные окружности rw1 и rw2(или центроиды) и межосевое расстояние aw связаны между собой следующими соотношениями ( см. основную теорему зацепления и раздел по кинематике зубчатой передачи):
aw = rw1 + rw2 ; u12 = rw2 / rw1 ; aw = rw1 × ( 1 + u12 ) ;
rw1= aw /( 1 + u12); rw2 = rw1 - aw .
Межосевое расстояние aw
Из схемы эвольвентного зацепления (рис.12.12) можно записать
aw = rw1 + rw2 ,
но ry = r × (cos a / cos a y ) и rw = r × (cos a / cos a w ),
после подстановки, получим
aw = r1 × (cos a / cos a w ) + r2 × (cos a / cos a w ) ,
aw = ( m×z1 /2 + m×z2 / 2 )× (cos a / cos a w ) ,
aw = m× (z1 + z2 )× (cos a / cos a w ) / 2 .
49
(см. рисунок отдельно)
Цилиндрическая эвольвентная зубчатая передача.
Два зубчатых колеса с одинаковым модулем и с числами зубьев соответствующими заданному передаточному отношению образуют зубчатую передачу или простейший зубчатый механизм. В этом трехзвенном механизме зубчатые колеса образуют между собой высшую пару, а со стойкой низшие пары. Зубчатая передача, кроме параметров образующих ее колес, имеет и собственные параметры: угол зацепления aw, межосевое расстояние aw, воспринимаемое смещение y×m и уравнительное смещение Dy×m . Передаточное отношение механизма u12, числа зубьев колес z1 и z2, начальные окружности rw1 и rw2(или центроиды) и межосевое расстояние aw связаны между собой следующими соотношениями ( см. основную теорему зацепления и раздел по кинематике зубчатой передачи):
aw = rw1 + rw2 ; u12 = rw2 / rw1 ; aw = rw1 × ( 1 + u12 ) ;
rw1= aw /( 1 + u12); rw2 = rw1 - aw .
Уравнительное смещение Dy× m
Из рис. 12.12 aw = ra1 + c*× m + rf2 ,
aw = r1 + r2 + y× m ,
откуда ra1 + c*× m + rf2 = r1 + r2 + y× m ,
где ra1 = m × ( z1 / 2 + h*a + x1 - Dy ), rf 2= m × (z2 /2 - h*a - c* + x2 ) .
Подставим эти выражения
m× ( z1 / 2 + h*a + x1 - Dy ) + c*× m + m× (z2 /2 - h*a - c* + x2 ) = (m × z1 / 2)+ (m × z2 /2) + y × m .
и, после преобразований, получим
x1 + x2 - Dy = y,
Коэффициент уравнительного смещения
Dy = ( x1 + x2 ) - y.
В 70 - е годы были разработаны и приняты ГОСТ на терминологию, прочностные и геометрические расчеты эвольвентных зубчатых передач. В ГОСТ предусмотрены два вида расчета геометрии:
- по стандартному радиальному зазору в передаче(х*м);
- по стандартной высоте зуба.
51 Коэффициент торцевого перекрытия.
Коэффициентом перекрытия eg называется величина отношения угла перекрытия зубчатого колеса к его угловому шагу, где под углом перекрытия понимают угол на который поворачивается колесо за время зацепления одной пары зубьев. Для цилиндрических колес различают полное eg, торцевое ea и осевое перекрытие:
eg = ea + eb ,
где осевое перекрытие имеется только в косозубых передачах.
ea = j1 / t1 = j2 / t2 = ga / pb = ( gaf + gaa ) / pb ,
где gaf = lB1N2 - lPN2 = rb2 × ( tg aa2 - tg aw ), aa2 = arccos (rb2 / ra2 ),
gaa = lB2N1 - lPN1 = rb1 × ( tg aa1 - tg aw ), aa1 = arccos (rb1 / ra1 ),
pb = p× m × cos a , rbi = m × z × cos a / 2 .
ea = [ z2 × ( tg aa2 - tg aw ) - z1 × ( tg aa1 - tg aw )] / (2×p).
Коэффициент перекрытия определяет величину зоны двухпарного контакта, когда одновременно зацепляются два последовательно расположенных зуба. Так как до окончания зацепления одной пары зубьев, следующая пара должна войти в контакт, нельзя допускать в прямозубых передачах ea £ 1. Допустимое значение коэффициента перекрытия должно несколько превышать единицу и, в зависимости от назначения передачи и точности ее изготовления, выбирается в пределах [ea ] = 1.05 ... 1.2. Максимальное значение коэффициента перекрытия для зубчатых колес, обработанных инструментом со стандартным исходным производящим контуром, составляет ea = 1.98. Наиболее благоприятны величины коэффициента перекрытия равные целым числам, например двум или трем. Обеспечить это можно только используя инструмент с нестандартным исходным производящим контуром. Дробные значения коэффициента перекрытия, например близкие к полутора, приводят к циклическому изменению жесткости передачи и к возникновению параметрических колебаний.
| 44 Толщина зуба колеса по окружности произвольного радиуса. 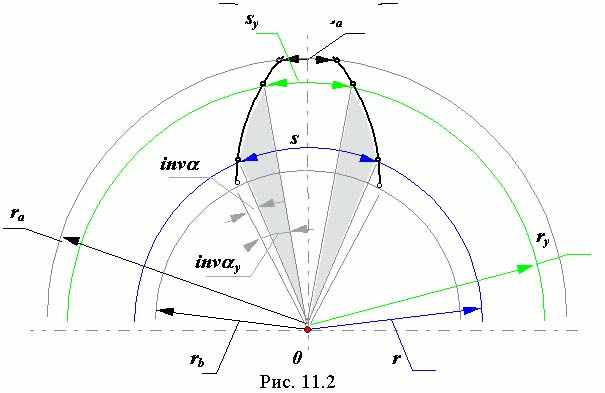 Толщина зуба по дуге делительной окружностиs = (p× m / 2 ) + D× m. Угловая толщина зуба по окружности произвольного радиуса из схемы на рис. 11.2 sy / ry = s / r - ( inv ay - inv a )× 2,где r = m×z / 2 , ry = m×z × cos a / (2× cos ay ) Подставляя в формулу угловой толщины эти зависимости, получим sy = s× ry / r - ( inv ay - inv a )× 2× ry, или sy = m × (cos a / cos a y) × [(p / 2 ) + D - ( inv ay - inv a )× z] . 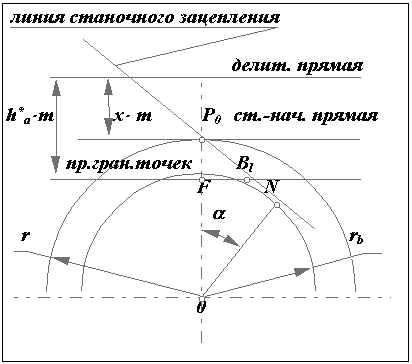 Подрезание эвольвентных зубьев в станочном зацеплении.В процессе формирования эвольвентного зуба по способу огибания, в зависимости от взаимного расположения инструмента и заготовки возможно срезание эвольвентной части профиля зуба той частью профиля инструмента, которая формирует переходную кривую. Условие при котором это возможно определяется из схемы станочного зацепления. Участок линии зацепления, соответствующий эвольвентному зацеплению определяется отрезком B1. где точка Bl определяется пересечением линии станочного зацепления и прямой граничных точек инструмента. Если точка Bl располагается ниже (см. рис.12.8) точки N , то возникает подрезание зуба. Условие при котором нет подрезания можно записать так P0N ³ P0Bl . Из D P0N0 P0N = r × sin a = m×z×sin a / 2, а из D P0BlF P0Bl = ( h*a - x )× m / sin a . Тогда z×sin a / 2 ³ ( h*a - x ) / sin a , при x=0 z ³ 2 × h*a / sin2 a , откуда zmin = 2 × h*a / sin2 a , где zmin - минимальное число зубьев нулевого колеса нарезаемое без подрезания. Избежать подрезания колеса можно если увеличить смещение инструмент так, чтобы точка Bl оказалась бы выше точки N или совпала с ней. Тогда смещение инструмента при котором не будет подрезания x ³ h*a - z × sin2 a / 2 , Þ x ³ h*a × [ 1 - z × sin2 a / (2× h*a )], x ³ h*a × ( 1 - z / z min ). В предельном случае, когда точка Bl совпадает с точкой N xmin = h*a × ( 1 - z / z min ), 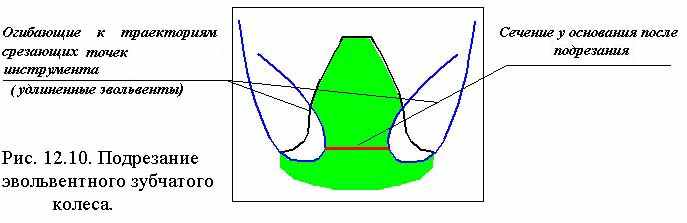 где xmin - минимальное смещение инструмента при котором нет подрезания. | 45 Станочное зацепление. Станочным зацеплением называется зацепление, образованное заготовкой колеса и инструментом, при изготовлении зубчатого колеса на зубообрабатывающем оборудовании по способу обката. Схема станочного зацепления колеса и инструмента с производящим контуром, совпадающим с исходным производящим контуром, изображена на рис. 12.4. 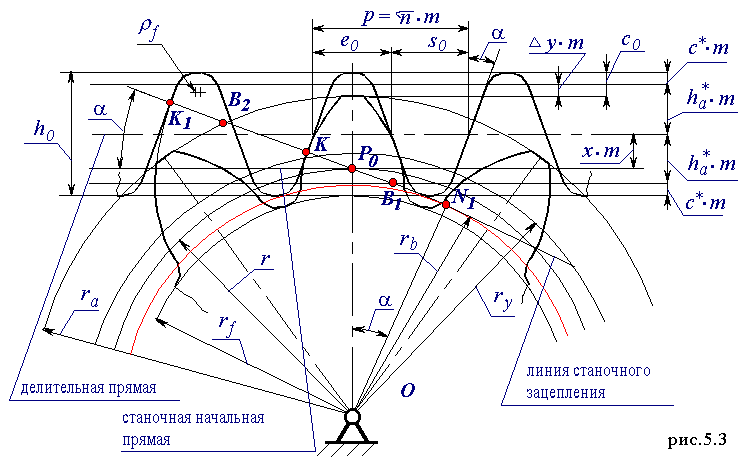 Линия станочного зацепления - геометрическое место точек контакта эвольвентной части профиля инструмента и эвольвентной части профиля зуба в неподвижной системе координат.Смещение исходного производящего контура x×m - кратчайшее расстояние между делительной окружностью заготовки и делительной прямой исходного производящего контура. Уравнительное смещение Dy×m - условная расчетная величина, введенная в расчет геометрии зацепления с целью обеспечения стандартного радиального зазора в зацеплении (величина, выражающая в долях модуля уменьшение радиуса окружностей вершин колес, необходимое для обеспечения стандартной величины радиального зазора). Окружность граничных точек rl - окружность проходящая через точки сопряжения эвольвентной части профиля зуба с переходной кривой. Основные размеры зубчатого колеса.Определим основные размеры эвольвентного зубчатого колеса, используя схему станочного зацепления
ra = m × ( z / 2 + h*a + x - Dy ) .
h = m × ( c* + 2× h*a - Dy ) .
Т  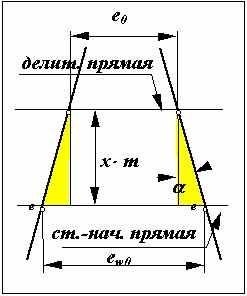 ак как стночно-начальная прямая перекатывается в процессе огибания по делительной окружности без скольжения, то дуга s-s по делительной окружности колеса равна ширине впадины e-e по станочно-начальной прямой инструмента. Тогда, c учетом схемы на рис. 12.5, можно записать s = e0 + 2× x × m × tg a , s = m × ( p / 2 + 2× x × tg a ), где D = 2× x × tg a . Виды зубчатых колес (Классификация по величине смещения). В зависимости от расположения исходного производящего контура относительно заготовки зубчатого колеса, зубчатые колеса делятся на нулевые или без смещения, положительные или с положительным смещением, отрицательные или с отрицательным смещением. | 46 Эвольвентное зацепление и его свойства. В зубчатой передаче контактирующие элементы двух профилей выполняются по эвольвентам окружности и образуют, так называемое эвольвентное зацепление. Это зацепление обладает рядом полезных свойств, которые и определяют широкое распространение эвольвентных зубчатых передач в современном машиностроении. Рассмотрим эти свойства. 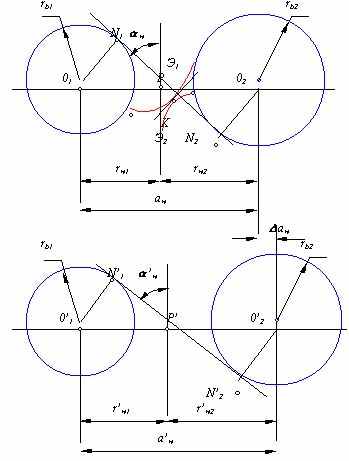 Свойство 1. Передаточное отношение эвольвентного зацепления определяется только отношением радиусов основных окружностей и является величиной постоянной. u12 = w1 /w2 = rw2 / rw1 = (rb2×cos aw )/ (rb1×cos aw ) = rb2 / rb1 = const. Свойство 2. При изменении межосевого расстояния в эвольвентном зацеплении его передаточное отношение не изменяется. u’12 = w1 /w2 = r’w2 / r’w1 = (rb2×cos a’w )/ (rb1×cos a’w ) = rb2 / rb1 = const. u’12 = u12 = rb2 / rb1 = const Свойство 3. При изменении межосевого расстояния в эаольвентном зацеплении величина произведения межосевого расстояния на косинус угла зацепления не изменяется. rb1 + rb2 = rw1 × cos aw + rw2 × cos aw = aw × cos aw , rb1 + rb2 = r’w1 × cos a’w + r’w2 × cos a’w = a’w × cos a’w , aw × cos aw = a’w × cos a’w = const. Свойство 4. За пределами отрезка линии зацепления N1N2 рассматриваемые ветви эвольвент не имеют общей нормали, т. е. профили выполненные по этим кривым будут не касаться, а пересекаться. Это явление называется интерференцией эвольвент или заклиниванием. |
| 50 (см. рисунок отдельно) Цилиндрическая эвольвентная зубчатая передача. Два зубчатых колеса с одинаковым модулем и с числами зубьев соответствующими заданному передаточному отношению образуют зубчатую передачу или простейший зубчатый механизм. В этом трехзвенном механизме зубчатые колеса образуют между собой высшую пару, а со стойкой низшие пары. Зубчатая передача, кроме параметров образующих ее колес, имеет и собственные параметры: угол зацепления aw, межосевое расстояние aw, воспринимаемое смещение y×m и уравнительное смещение Dy×m . Передаточное отношение механизма u12, числа зубьев колес z1 и z2, начальные окружности rw1 и rw2(или центроиды) и межосевое расстояние aw связаны между собой следующими соотношениями ( см. основную теорему зацепления и раздел по кинематике зубчатой передачи): aw = rw1 + rw2 ; u12 = rw2 / rw1 ; aw = rw1 × ( 1 + u12 ) ; rw1= aw /( 1 + u12); rw2 = rw1 - aw . Воспринимаемое смещение y× m Из схемы эвольвентного зацепления (рис.12.12) можно записать aw = r1 + r2 + y× m = m× (z1 + z2 ) / 2 + y× m , m× (z1 + z2 ) / 2 + y× m = m× (z1 + z2 )× (cos a / cos a w ) / 2 , Коэффициент воспринимаемого смещения y = (z1 + z2 )×[ (cos a / cos a w ) - 1 ] / 2. Классификация зубчатых передач. Цилиндрические эвольвентные зубчатые передачи в зависимости от величины воспринимаемого смещения классифицируются следующим образом
x1 = x2 = 0 или x1 = - x2,  D1 = D2 = 0 или D1 = - D2 y×m = 0, y = 0 aw= a = r1 + r2 aw = a ;
x1 > 0, x2 > 0 или x1 > | - x2 |D1 > 0, D2 > 0 или D1 > | - D2 | y×m > 0, y > 0, aw> a , aw > a ;
x1 <0 , x2 < 0 или x1 < - x2 | , D1 < 0, D2 < 0или D1 < | - D2 y×m < 0, y < 0, aw< a aw < a . | ||
| | 17 Режимы движения машины. В  зависимости от того какую работу совершают внешние силы за цикл движения машины различают три режима движения: разгон, торможение и установившееся движение. Циклом называют период времени или период изменения обобщенной координаты, через который все параметры системы принимают первоначальные значения.
|