Лгоритма его функционирования), устранения некорректности первичного описания и последовательного представления (при необходимости) описаний на различных языках
| Вид материала | Документы |
| 66 . Для кулачкового механизма с коромыслом.(с качающимся толкателем) |
- Х описаний документов и пополнению сводного электронного каталога с целью устранения, 58kb.
- Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
- Система Автоматизации Инженерного Труда cad computer Automation Design cam computer, 35.46kb.
- Проектирования это создание описания, необходимого для построения в заданных условиях, 258.57kb.
- История описания системных васкулитов, 320.25kb.
- История описания системных васкулитов, 320.23kb.
- Проект стандарт Форматы представления сведений из административной модели, 1588.72kb.
- Маркетинговые критерии оптимального функционирования фармацевтической компании, 241.01kb.
- Лекция № Библиографическое описание документа, 84.67kb.
- Ы (услуги) предприятия и его партнёров, и последующем их исполнении и контроле с помощью, 161.35kb.
| 52 Качественные показатели цилиндрической эвольвентной передачи. К качественным показателям цилиндрической эвольвентной зубчатой передачи относятся:
Расчет геометрии внешнего зацепления при фиксированном значении x2 = 0.5 и изменении x1 в диапазоне от 0 до 1.4 с шагом 0.1. Определяется область допустимых решений для коэффициента x1 и выбор этого по оптимальному сочетанию качественных показателей. На рис. 13.6 приведен пример графика. При принятых допустимых значениях [ea] =1.1 и [sa/m]=0.3, ограничения на выбор коэффициента смещения x1 по подрезанию Þ x1 min = 0.24 ; по заострению колеса z1 Þ x1 maxsa = 1.24; по торцевому перекрытию Þ x1 maxea = 0.84. Таким образом, область допустимых значений (ОДЗ), в которой можно выбирать значение x1 0.24> x1 > 0.84 этой области выбирается то значение x1, которое обеспечивает наилучшее сочетание качественных показателей. Часто выбор коэффициента производят по рекомендациям ГОСТ. Для рассматриваемого случая силовой зубчатой передачи с числами зубьев z1 = 14 и z2 = 22 x1 = x2 = 0.5 . 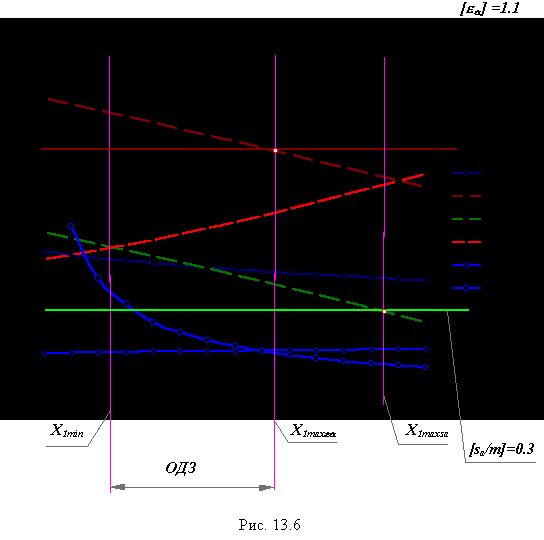 [ea] =1.1Понятие о блокирующем контуре зубчатой передачи. При проектировании зубчатой передачи необходимо решить несколько задач:
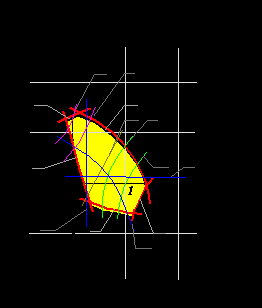 Для эвольвентных зубчатых передач, область сочетаний коэффициентов смещений зубчатых колес x1 и x2, удовлетворяющих ограничениям по срезанию в станочном зацеплении, заострению, заклиниванию в зацеплении эвольвент и на переходных кривых, по допустимым минимальным или максимальным значениям качественных показателей, называют блокирующим контуром (рис.13.2). Границы блокирующего контура отсекают те значения коэффициентов смещению которые недопустимы по указанным условиям. Значения, расположенные внутри контура, допустимы, но каждой паре коэффициентов смещения соответствует свое сочетание качественных показателей. Для выбора коэффициентов смещения на блокирующий контур наносятся изолинии качественных показателей, с использованием которых внутри контура выбираются коэффициенты смещения с оптимальным сочетанием качественных показателей. На рис. 13.2 ограничивающие линии блокирующего контура: 1 - коэффициент торцевого перекрытия ea =1; 2 - толщина зуба колеса z1 по окружности вершин sa1 = 0; 3 - допустимое подрезание колеса z2 ; 4 - допустимое подрезание колеса z1 ; 5 - интерференция или заклинивание с переходной кривой колеса z2. Линии качественных показателей: 6 - линия sa2 = 0.25m; 7 - линия sa2 = 0.4m; 8 - линия выравненных удельных скольжений l1=l2; 9 - линия sa1 = 0.4m; 10 - линия sa1 = 0.25m; 11 - линия x2 = x2min ; 12 - линия x1 = x1min ; 13 - линия ea = 1.2. | 53 К механизмам с высшими КП относятся любые механизмы в состав которых входит хотя бы одна высшая пара. Простейший типовой механизм с высшей парой состоит из двух подвижных звеньев, образующих между собой высшую кинематическую пару, а со стойкой низшие ( вращательные или поступательные ) пары. К простейшим механизмам с высшей парой относятся :
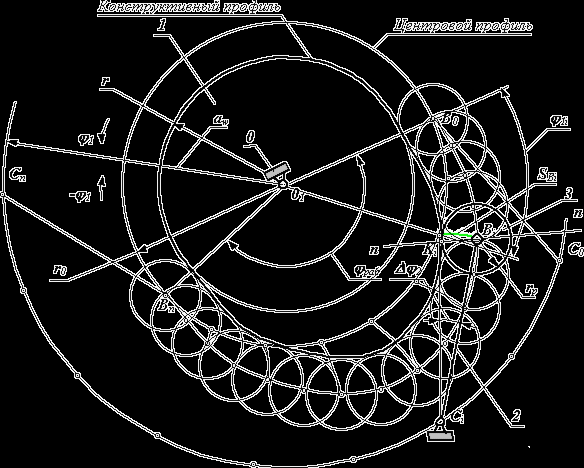
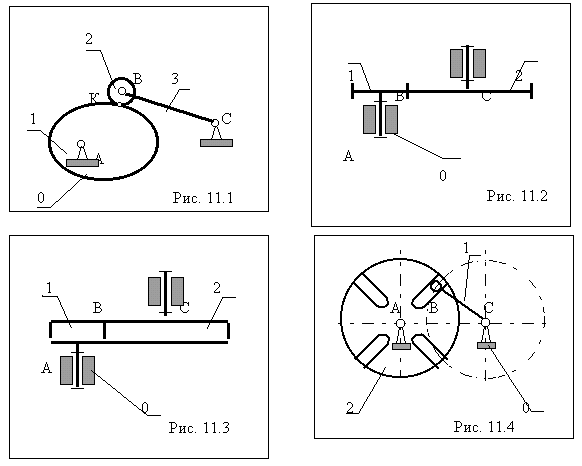 Кулачковые механизмы. Кулачковым называется трехзвенный механизм с высшей кинематической парой входное звено которого называется кулачком, а выходное - толкателем (или коромыслом). Часто для замены в высшей паре трения скольжения трением качения и уменьшения износа, как кулачка, так и толкателя, в схему механизма включают дополнительное звено – ролик и вращательную кинематическую пару. Подвижность в этой кинематической паре не изменяет передаточных функций механизма и является местной подвижностью. Назначение и область применения. Кулачковые механизмы предназначены для преобразования вращательного или поступательного движения кулачка в возвратно-вращательное или возвратно-поступательное движение толкателя. При этом в механизме с двумя подвижными звеньями можно реализовать преобразование движения по сложному закону (такие механизмы встречаются в гравировальных автоматах, металлообрабатывающий станках и других машинах). Важным преимуществом кулачковых механизмов является возможность обеспечения точных выстоев выходного звена. Это преимущество определило их широкое применение в простейших устройствах цикловой автоматики и в механических счетно-решающих устройствах (арифмометры, календарные механизмы). Кулачковые механизмы можно разделить на две группы. Механизмы первой обеспечивают перемещение толкателя по заданному закону движения. Механизмы второй группы обеспечивают только заданное максимальное перемещение выходного звена – ход толкателя. При этом закон, по которому осуществляется это перемещение, выбирается из набора типовых законов движения в зависимости от условий эксплуатации и технологии изготовления. Зубчатые передачи Зубчатыми передачами называются механизмы с высшими кинематическими парами в состав которых входят зубчатые колеса, рейки или секторы - звенья, снабженные профилироваными выступами или зубьями. Зубчатые передачи бывают простые и сложные. Простая зубчатая передача - трехзвенные механизм, состоящий из двух зубчатых колес и стойки, в котором зубчатые колеса образуют между собой высшую пару, со стойкой - низшие ( поступательные или вращательные ).В различных машинах и приборах весьма часто становится задача о воспроизведении вращательных движений с заданными угловыми скоростями вокруг различно расположенных осей. Зубчатые механизмы получили широкое распространение как в машиностроении , так и в приборостроении благодаря компактности, большой надежности и точности воспроизведения заданного закона движения. К достоинствам циклоидального зацепления можно отнести то, что В этом зацеплении может быть достигнута большая плавность зацепления.. Недостатком этих профилей является их чувствительность к изменению расстояния между центрами. Фрикционные механизмы Фрикционными механизмами или передачами сцепления называются механизмы с высшей парой в которых в качестве сил, приводящих в движения звенья, или сил, тормозящих их движения используются силы трения . В современных машинах широкое применение имеют механизмы фрикционных колес, воспроизводящих постоянное передаточное отношение. Для надежной работы механизмов фрикционных передач необходимо исключить проскальзывание между соприкасающимися поверхностями. Для этого надо, чтобы сила трения была достаточной. Последнее достигается прижатием одного колеса к другому с помощью пружин. Т.о. элементы колес оказываются сильно нагруженными и изнашиваются в процессе работы. Поводковые механизмы Зубчатые механизмы с остановками позволяют воспроизводить движение с различными периодами покоя и движения, а также с различными отношениями угловых скоростей в различные периоды. В машинах автоматического и полуавтоматического действия широко используются механизмы, которые позволяют в пределах рабочего цикла иметь остановки выходного звена заданной продолжительности при непрерывном движении выходного звена. Остановка может быть полной или почти полной, а ее продолжительность--как заданный, так и неопределенный. В станках-автоматах, обрабатывающих центрах и автоматических линиях нашли широкое применение устройства, преобразующее непрерывное вращательное движение входного звена в одностороннее прерывистое движение выходного звена. С помощью этих механизмов транспортируются заготовки, происходит смена инструментов с одной фиксированной позиции на другую. Мальтийские механизмы имеют более благоприятные кинематические характеристики и надежно обеспечивают заданное время покоя (по сравнению с храповыми механизмами). | 54 Конические зубчатые передачи. Конической называется зубчатая передача, предназначенная для передачи и преобразования вращательного движения между звеньями, оси вращения которых пересекаются.  Схема конической передачи представлена на рис. 14.2. Оси колес зубчатой передачи пересекаются в точке 0. Угол å между осями колес ( или между векторами угловых скоростей звеньев w1 и w2 ) называется межосевым углом. Этот угол может изменяться в пределах 0° < å < 180°. При å = 0° передача превращается в цилиндрическую с внешним зацеплением, а при å = 180° - в цилиндрическую с внутренним зацеплением. Таким образом, коническая передача является общим случаем зубчатой передачи, нежели цилиндрические. Начальные или аксоидные поверхности в конической передаче имеют форму конусов. Аксоидными называются поверхности, которые образуются осями мгновенного относительного вращения колес, в системах координат связанных с колесами ( звеньями передачи ). Если колеса передачи обработаны без смещения исходного контура, то аксоидные поверхности совпадают с делительными. При относительном движении аксоиды перекатываются друг по другу, при этом скольжение возможно только в направлении оси относительного вращения. Поэтому вектора угловых скоростей звеньев связаны между собой векторным уравнением w2 = w1 + w21 , // 002 // 001 // 0P если известна величина w1 , то из этого уравнения можно определить w2 и w21.Из векторного треугольника D a0b w1 / sin d1 = w2 / sin d2 Þ w1 /w2 = sin d2 / sin d1 . Передаточное отношение конической передачи u12 = ± ½w1½/ ½w2½ = sin d2 / sin d1 .Так как å = d1 + d2 , d2= å - d1 , то u12 = sin (å - d1) / sin d1 = (sin å × cos d1 - cos å × sin d1) / sin d1 u12 = (sin å / tgd1) - cos å .Тогда углы начальных ( делительных при х=0 ) конусов d1 = arctg [ sin å / ( u12 + cos å )], d2= å - d1 . Геометрия зацепления в конической зубчатой передаче. Как и в цилиндрических, так и в конических зубчатых передачах наиболее часто применяют эвольвентное зацепление. Эвольвентная поверхность зуба конического колеса образуется при перекатывании производящей плоскости по основному конусу. Эвольвентные кривые формируются на соосных сферических поверхностях с центром в вершине основного конуса. Поэтому для расчета геометрии эвольвентной конической передачи необходимо применять сферическую геометрию. При этом методе расчет геометрии проводится для эквивалентного цилиндрического зацепления двух секторов. Эти сектора образуются развертками конусов, которые построены на внешней сфере радиуса R we . Радиусы оснований этих конусов r we1 = r e1 и r we2 = r e2 , а образующие являются касательными к сфере (рис14.3). Числа зубьев колес эквивалентного цилиндрического зацепления рассчитываются на основании следующих формул rvte1 = rte1 / cos d1 , rvte2 = rte2 / cos d2 ,где rte1и rte2 - радиусы торцевых делительных окружностей на внешней сфере (рис 14.2), rvte1и rvte2- радиусы делительных окружностей эквивалентного цилиндрического зацепления. Так как rte1 = mte × z1 , rte2 = mte × z2 , и rvte1 = mte × zvt1 , rvte2 = mte × zvt2 ,то zvt1 = z1 / cos d1 , zvt2 = z2 / cos d2 , где z1 и z2 - числа зубьев колес конической передачи, zvt1 и zvt2 - числа зубьев колес эквивалентного цилиндрического расчетного зацепления ( эти величины могут быть дробными). После определения чисел зубьев эквивалентного цилиндрического зацепления, приближенный расчет геометрических параметров для внешнего торца конического зацепления можно проводить по рассмотренным выше формулам цилиндрического эвольвентного зацепления. Радиус внешней сферы (длина образующей начального или делительного конуса) Rwe = rwe1 / sin d1 = rwe2 / sin d2 . Ширина зубчатого венца b = y× Rwe , где b = 0.3 ... 0.4 - коэффициент ширины зубчатого венца. По форме линии зуба конические зубчатые передачи различаются на: прямозубые; косозубые; с круговым зубом; с эвольвентной линией зуба; с циклоидальной линией зуба. Преимущества и недостатки кинических зубчатых передач. Преимущества:
Недостатки:
 |
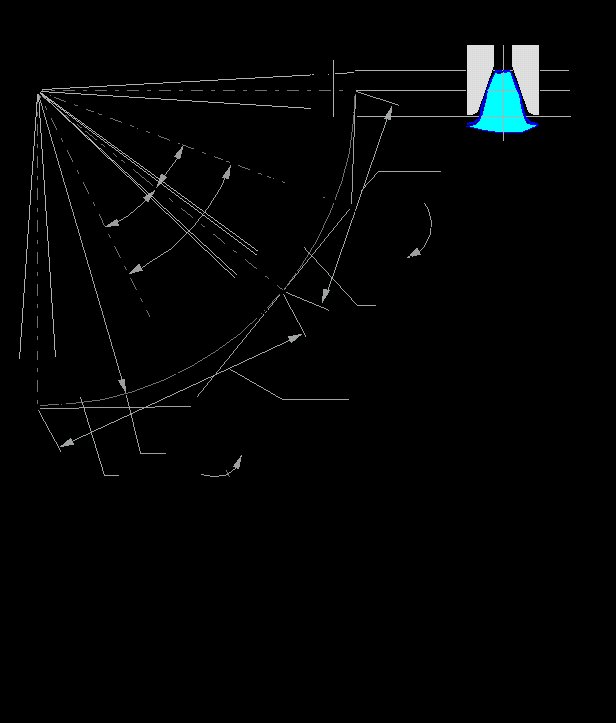| 66 . Для кулачкового механизма с коромыслом.(с качающимся толкателем) Построение профилей кулачка проводится в следующей последовательности:
 | ||
| | |