Агрегатное состояние в-ва, в к-ром его ч-цы не связаны или весьма слабо связаны силами вз-ствия и дви­жутся свободно, заполняя весь предо­ставленный им объём

Вид материала

Документы

Содержание Генри на метр Геометрическая акустика Геометрическая оптика Геометрический фактор А. А. Волькенштейн. СГС системы единиц. Герца диполь Герца принцип Гаусса принцип) Гетерогенная система Гетерохромная фотометрия Гиббса ансамбль Тождественности принцип). N, а интегрирова­ние — Гиббса большой канониче­ский ансамбль Гиббса канонический ан­самбль Гиббса правило фаз Гиббса распределения 8 при пост. объёме V и с задан­ным числом ч-ц N (микроканониче­ский ансамбль Гиббса) А — постоянная, позволяющая определить энтропию ... Полное содержание

Подобный материал:

• 2. Молекулярно-кинетическая теория идеальных газов, 52.42kb.
• Магия и технология – за и против (или наоборот – вместе или порознь) Гилдор Карнесир, 243.69kb.
• Тема: Инновации и инновационные процессы, 158.08kb.
• Т. И. Розбицкая Музыка в жизни и творчестве И. С. Тургенева Все виды искусства так, 46.59kb.
• Ii этап Команда «исследователи» моу «сош №2», 94.86kb.
• 1 Использование ресурсов минерально-сырьевой базы края и охрана недр, 291.61kb.
• Позиционирования (gps), 196.2kb.
• Конспект тема: Бизнес план и его роль в современном предпринимательстве, 598.08kb.
• Задания для второго (районного, городского) этапа Всероссийской олимпиады школьников, 68.78kb.
• Курсовые работы на III и IV курсах обязательно должны быть связаны, 86.91kb.

ГЕНРИ (Гн, Н), единица СИ индуктив­ности и взаимной индуктивности. На­звана в честь амер. учёного Дж. Генри (J. Henry). 1 Гн равен индуктивности электрич. контура, возбуждающего магн. поток в 1 вебер при силе пост. тока в нём 1 А. Другое эквивалентное определение: 1 Гн — индуктивность электрич. цепи, в к-рой возникает эдс самоиндукции в 1 В при равномерном изменении тока в этой цепи со скоро­стью 1 А/с. 1 Гн=1 В•с/А=1 Вб/А=10⁹ см (ед. СГСМ) = 1,11•10^-12 ед. СГСЭ.

ГЕНРИ НА МЕТР (Гн/м, Н/m), единица СИ абсолютной магн. проницаемости. 1 Гн/м равен абс. магн. проницаемости среды, в к-рой при напряжённости магн. поля 1 А/м создаётся магн. индукция 1 Тл; 1 Гн/м=1 Тл•м/А=1 Вб/(А•м)=10⁷/4 ед. СГСМ.

ГЕНРИМЕТР, то же, что индуктив­ности измеритель.

ГЕОАКУСТИКА (от греч. ge — Земля и акустика), раздел акустики, в к-ром изучается распространение звук., ин­фразвук. и ультразвук. волн в земной коре, как возникающих в результате

природных процессов (напр., акустич. предвестники землетрясений), так и связанных с использованием упругих волн для изучения строения и св-в верх. слоев земной коры (акустич. разведка, сейсмич. разведка, глубин­ное сейсмич. зондирование, УЗ эхо-локация). Методы Г. явились первым применением УЗ для практич. целей, однако большое поглощение УЗ высо­ких частот (20 кГц и выше) в земной коре ограничивает глубину прозвучивания пород неск. десятками м. При низких звук. и инфразвук. частотах глубина прозвучивания повышается, но уменьшается возможность более детального изучения разреза. Изуче­ние строения слоистой среды произ­водится также непосредственно в сква­жинах (звук. каротаж).

ГЕОМАГНЕТИЗМ, то же, что земной магнетизм.

ГЕОМЕТРИЧЕСКАЯ АКУСТИКА, раздел акустики, в к-ром изучаются законы распространения звука на ос­нове представления о звук. лучах как линиях, вдоль к-рых распространяется звук. энергия. Г. а.— предельный слу­чай волн. акустики при переходе к бес­конечно малой длине волны, поэтому методы Г. а. явл. приближёнными и тем точнее отражают действительность, чем меньше длина волны. Осн. задача Г. а.— вычисление траекторий звук. лучей. Наиболее простой вид лучи имеют в однородной среде, где они представляют собой прямые линии. В Г. а. имеют место в осн. те же зако­ны и ур-ния, что и в геометрической оптике (напр., законы отражения и преломления волн).

Методами Г. а. пользуются для прак­тич. приложений в самых разл. обла­стях акустики; напр., в архитектур­ной акустике, при расчёте звук. фоку­сирующих систем. На основе законов Г. а. удаётся создать приближённую теорию распространения звука в не­однородных средах (напр., в море, в атмосфере). И. П. Голямина.

ГЕОМЕТРИЧЕСКАЯ ОПТИКА, раз­дел оптики, в к-ром изучаются законы распространения оптического излуче­ния (света) на основе представлений о световых лучах. Под световым лучом понимают линию, вдоль к-рой распро­страняется поток световой энергии. Понятием луча можно пользоваться только в случае, когда можно прене­бречь дифракцией света на оптич. неоднородностях, а это допустимо тог­да, когда длина световой волны много меньше размеров неоднородностей. За­коны Г. о. позволяют создать упро­щённую, но в большинстве случаев достаточно точную теорию оптич. сис­тем. Г. о. в осн. объясняет образова­ние изображений оптических, даёт возможность вычислять аберрации оп­тических систем и разрабатывать мето­ды их исправления, выводить энергетич. соотношения в световых пучках, проходящих через оптич. системы. Вместе с тем все волн. явления, в т. ч. дифракционные, влияющие на кач-во

изображений и определяющие разре­шающую способность оптич. приборов, не рассматриваются в Г. о.

Представление о независимо распро­страняющихся световых лучах воз­никло ещё в античной науке. Древне-греч. учёный Евклид сформулировал закон прямолинейного распростране­ния света и закон зеркального отра­жения света. В 17 в. Г. о. бурно раз­вивалась в связи с изобретением ряда оптич. приборов (зрительная труба, телескоп, микроскоп и т. д.) и началом их широкого использования. Голл. математиком В. Снеллем и франц. учёным Р. Декартом были эксперимен­тально установлены законы, описыва­ющие поведение световых лучей на границе раздела двух сред (см. Снелля закон преломления). Построение теор. основ Г. о. к сер. 17 в. было завершено установлением Ферма принципа. Зако­ны прямолинейного распространения, зеркального отражения и преломле­ния света, исторически открытые ра­нее, явл. следствиями этого принципа.

С 18 в. Г. о., совершенствуя методы расчёта оптич. систем, развивалась как прикладная наука. После создания классической электродинамики было показано, что формулы Г. о. могут быть получены и из Максвелла уравне­ний как предельный случай, соответ­ствующий переходу к исчезающе малой длине волны.

Г. о. явл. примером теории, позво­лившей при малом числе фундам. по­нятий и законов (представление о лу­чах света, законы отражения и пре­ломления) получить много практиче­ски важных результатов. В теория оптич. устройств мн. расчёты до на­стоящего времени основаны на Г. о.

• Л а н д с б е р г Г. С., Оптика, 5 изд., М., 1976 (Общий курс физики, т. 3); Б о р н М., Вольф Э., Основы оптики, пер. с англ., М., 1973; Герцбергер М., Современ­ная геометрическая оптика, пер. с англ., М., 1962.

К. И. Погорелое.

ГЕОМЕТРИЧЕСКИЙ ФАКТОР, вели­чина, определяющая геометрию пучка излучения; широко используется в фо­тометрии, космофизике при регистра­ции потоков ч-ц и излучений. Г. ф. G зависит от размеров и взаимного рас­положения диафрагм, совместно выде­ляющих из всех возможных прямых то множество направлений, к-рое оп­ределяется пучком излучения и угл. апертурой приёмника излучения. Г. ф. инвариантен относительно любых по­верхностей, пересекаемых прямыми, входящими в данное множество на­правлений, и принимается за меру это­го множества (понятие о мере множест­ва лучей впервые введено сов. учёным А. А. Гершуном в 30-х гг. 20 в.). Напр., для сопряжённых диафрагм ис­точника и приёмника А_и и А_п (или со­пряжённых нач. и кон. диафрагм оп­тич. системы)

dG=dА_иcos_иd_и = dA_пcos_пd_п, где dA_и и dA_п — площади диафрагм

113


источника и приёмника, _и и _п — углы между направлением излучения и перпендикулярами к излучающей и освещаемой поверхностям, d_и и d_п — заполненные излучением телес­ные углы со стороны диафрагм A_и и А_п. Инвариантность Г. ф. сохраняется и для широких пучков. Г. ф. исполь­зуется также при построении системы фотометрических величин: яркость вдоль луча L=dФ/dG.

• Международный светотехнический сло­варь, 3 изд., М., 1979; Сапожни­ков Р. А., Теоретическая фотометрия, 3 изд., М., 1977.

А. А. Волькенштейн.

ГЕОФОН (от греч. ge — Земля и pho­ne — звук), приёмник звук. волн, распространяющихся в верх. слоях земной коры. Совр. Г. (разведочные сейсмографы) снабжены электроакус­тическими преобразователями, превра­щающими колебания почвы в колеба­ния электрич. тока, усилителем и реги­стрирующим шлейфовым осциллогра­фом. Хар-ки Г. различны в зависимо­сти от их конструкции и назначения. — Электродинамич. Г. явл. приёмником колебат. скорости, а пьезоэлектрич. Г.— приёмником ускорения ч-ц среды. Г. пользуются при акустич. исследова­нии горных пород, в горноспасат. ра­ботах и др.

ГЕРМАНИЙ (Ge), синтетич. моно­кристалл, ПП, точечная группа сим­метрии m3m, плотность 5,327 г/см³, T_пл=936 °С, тв. по шкале Мооса 6, ат. м. 72,60. Прозрачен в ИК области  от 1,5 до 20 мкм; оптически анизотро­пен, для =1,80 мкм коэфф. преломле­ния n=4,143. Один из осн. материалов ПП электроники (см. Полупроводнико­вые приборы).

ГЕРЦ (Гц, Hz), единица частоты СИ и СГС системы единиц. Названа в честь нем. физика Г. Герца (Н. Hertz). 1 Гц — частота периодического про­цесса, при к-рой за 1 с происходит один цикл процесса. Широко приме­няются кратные ед. от Г.— килогерц (1 кГц=10³ Гц), мегагерц (1 МГц= = 10⁶ Гц) и др.

ГЕРЦА ДИПОЛЬ, излучатель радио­волн, предложенный нем. физиком Г. Герцем (1888), доказавшим сущест­вование эл.-магн. волн. Герц приме­нял медные стержни с металлич. шарами или полосами на концах и иск­ровым промежутком посредине, под­ключённым к индукц. машине. Наи­меньший из применявшихся Герцем вибраторов имел длину l=26 см, в нём возбуждались колебания частоты v=5•10⁸ Гц (что соответствует = 60 см).

• См. лит. при ст. Антенна.

ГЕРЦА ПРИНЦИП, принцип наи­меньшей кривизны, один из вариац. принципов механики, устанавливаю­щий, что при отсутствии активных (заданных) сил из всех кинематически возможных, т. е. допускаемых связя­ми, траекторий действительной будет траектория, имеющая наименьшую кривизну. Этот принцип наз. также

принципом прямейшего пути; его мож­но рассматривать как обобщение зако­на инерции.

Г. п. тесно связан с принципом наи­меньшего принуждения (см. Гаусса принцип), поскольку величина Z, наз. принуждением, пропорц. квадрату кривизны; при идеальных связях (см. Связи механические) оба принципа име­ют одинаковое матем. выражение: 6Z=0. Г. п. был применён нем. учёным Г. Герцем (1894) для построения его механики, в к-рой действие активных сил заменяется введением соответству­ющих связей.

С. М. Тарг.

ГЕТЕРОГЕННАЯ СИСТЕМА (от греч. heterogenes — разнородный), неодно­родная термодинамич. система, состоя­щая из различных по физ. св-вам или хим. составу частей (фаз). Смежные фазы Г. с. отделены друг от друга физ. поверхностями раздела, на к-рых скачком изменяется одно или неск. св-в системы (состав, плотность, крист. структура, электрич. или магн. мо­мент и т. д.). Примеры Г. с.: вода и водяной пар над ней (вода в двух агрегатных состояниях), уголь и ал­маз (две различные по крист. струк­туре фазы одного в-ва — углерода), сверхпроводящая и нормальная фазы сверхпроводника, несмешивающиеся жидкости (напр., вода и растит. мас­ло), композиц. материалы (волокни­стые и дисперсноуплотнённые, содер­жащие различные по структуре хим. в-ва в тв. состоянии). Различие между Г. с. и гомогенной (однородной) си­стемой не всегда ясно выражено. Так, переходную область между гете­рогенными механич. смесями (взве­сями) и гомогенными (молекулярными) р-рами занимают т. н. коллоидные р-ры, в к-рых ч-цы растворённого в-ва столь малы, что к ним неприменимо понятие фазы.

ГЕТЕРОПЕРЕХОД, контакт двух раз­личных по хим. составу полупровод­ников. На границе раздела ПП обычно изменяются ширина запрещённой зо­ны, подвижность носителей яаряда, их эффективные массы и др. хар-ки. В «резком» Г. изменение св-в про­исходит на расстоянии, сравнимом или меньшем, чем ширина области объ­ёмного заряда (см. Электронно-ды­рочный переход). В зависимости от легирования обеих сторон Г. можно создать р — n-Г. (анизотипные) и n-Г. или р — р-Г. (изотипные). Комби­нации разл. Г. и монопереходов обра­зуют гетероструктуры.

Образование Г., требующее стыков­ки крист. решёток, возможно лишь при совпадении типа, ориентации и периода крист. решёток сращиваемых материалов. Кроме того, в идеальном Г. граница раздела должна быть сво­бодна от структурных и др. дефектов (дислокаций, точечных дефектов и т. п.), а также от механич. напряже­ний. Наиболее широко применяются монокристаллич. Г. между полупро­водниковыми материалами типа A^IIIB^V и их твёрдыми растворами на основе

арсенидов, фосфидов и антимонидов Ga и Al. Благодаря близости ковалентных радиусов Ga и Al изменение хим. состава происходит без измене­ния периода решётки. Гетерострук­туры получают также на основе мно­гокомпонентных (четверных и более) тв. растворов, в к-рых при изменении состава в широких пределах период решётки не изменяется. Изготовление монокрист. Г. и гетероструктур стало возможным благодаря развитию ме­тодов эпитаксиального наращивания ПП кристаллов (см. Эпитаксия).

Г. используются в разл. ПП прибо­рах: ПП лазерах, светопзлучающих ди­одах, фотоэлементах, оптронах и т. д.

• Алферов Ж. И., Гетеропереходы в полупроводниковой электронике близкого будущего, в кн.: Физика сегодня и завтра, под ред. В. М. Тучкевича, Л., 1973; Ели­сеев П. Г., Инжекционные лазеры на ге­теропереходах, «Квант. электрон.», 1972, № 6, с. 3.

Ж. И. Алфёров.

ГЕТЕРОХРОМНАЯ ФОТОМЕТРИЯ (от греч. heteros — иной, другой и chroma — цвет), подраздел фотомет­рии, в к-ром рассматриваются методы сравнения интенсивности разноцвет­ных (гетерохромных) излучений. При визуальном фотометрировании срав­ниваемых излучений их различие в цвете ведёт к дополнит. ошибке, к-рую можно уменьшить с помощью т. н. мигающего фотометра. Разноцветные излучения удобно сравнивать по ин­тенсивности, используя фотоэлектрич. приёмники, если тем или иным спо­собом придать кривой спектральной чувствительности приёмника форму кривой видности (см. Спектральная световая эффективность) человеческо­го глаза. В Г. ф. применяются также счётчики фотонов.

ГИББСА АНСАМБЛЬ, см. Статисти­ческий ансамбль.

ГИББСА БОЛЬШОЕ КАНОНИЧЕ­СКОЕ РАСПРЕДЕЛЕНИЕ, распреде­ление вероятностей состояний стати­стического ансамбля систем, к-рые на­ходятся в тепловом и материальном равновесии со средой (термостатом и резервуаром ч-ц) и могут обменивать­ся с ними энергией и ч-цами (через полупроницаемые перегородки) при пост. объёме. Г. б. к. р.— статистич. распределение, соответствующее Гиббса большому каноническому ансамблю. Установлено амер. физиком Дж. У. Гиббсом (J. W. Gibbs) в 1901 как фундам. закон статистической физики.

В классич. статистике вероятность распределения по состояниям опре­деляется ф-цией распределения f(p, q), зависящей от координат q и импульсов р всех ч-ц системы. Вероятность пребы­вания N частиц в бесконечно малом фазовом объёме dpdq равна



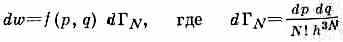
элемент фазового объёма системы в ед. h^3N, a N! учитывает, что переста­новка тождеств. ч-ц не меняет состо­яния (см. Тождественности принцип).

114


Полная вероятность пребывания систе­мы в к.-л. из состояний равна единице (она достоверно находится в одном из состояний), откуда следует, что



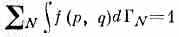
(условие нормировки).

Равновесная ф-ция распределения, согласно Г. б. к. р., зависит от коор­динат и импульсов через Гамильтона функцию H_N(p,q) системы



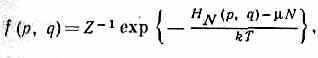
где  — химический потенциал, Z — постоянная, определяемая из условия нормировки и равная:



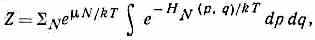
где суммирование ведётся по всем целым положит. N, а интегрирова­ние — по фазовому пр-ву N ч-ц. Т. о., Z выражается через статистич. инте­гралы для N ч-ц и зависит от , V, Т.

Г. б. к. р. можно вывести из мик­роканонического распределения Гиббса, если рассматривать данную систему вместе с термостатом и резервуаром ч-ц как одну большую замкнутую и изолиров. систему и применить к ней микроканонич. распределение. Тогда малая подсистема обладает Г. б. к. р., к-рое можно найти интегрированием по фазовым переменным термостата и резервуара ч-ц и суммированием по числам ч-ц (теорема Гиббса).

В квант. статистике статистич. ан­самбль характеризуется распределе­нием вероятности w_i,N, квант. состоя­ний г с энергией ξ_i,N, соответствую­щих числу ч-ц N, с условием норми­ровки _i,n w_i,n= l. Г. б. к. р. для квант. систем имеет вид:



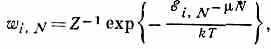
где Z — статистическая сумма для большого канонич. ансамбля Гиббса, определяемая из условия нормировки и равная:



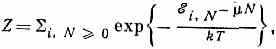
Г. б. к. р. в квант. случае можно представить через матрицу плотности =Z^-1ехр{(H-N)/kT}, где H — гамильтониан системы.

Г. б. к. р. как в классич., так и в квант. случае позволяет вычислить потенциал термодинамический F в переменных , V, Т, равный: F=-kTlnZ. Г. б. к. р. не требует выпол­нения дополнит. условия, связанного с постоянством числа ч-ц, и поэтому удобно для практич. вычислений.

• См. лит. при ст. Статистическая физика.

Д. Н. Зубарев.

ГИББСА БОЛЬШОЙ КАНОНИЧЕ­СКИЙ АНСАМБЛЬ, статистический ансамбль для макроскопич. систем пост. объёма в тепловом равновесии с термостатом и в материальном равно­весии с резервуаром ч-ц (обмен ч-цами можно осуществить при помощи по­лупроницаемых перегородок). У рас­сматриваемых систем переменными яв­ляются число ч-ц и энергия. Введён Дж. У. Гиббсом (1901) как одно из осн. понятий статистической физики. В случае Г. б. к. а. распределение по состояниям описывается Гиббса боль­шим каноническим распределением.

ГИББСА КАНОНИЧЕСКИЙ АН­САМБЛЬ, см. Канонический ан­самбль Гиббса.

ГИББСА МИКРОКАНОНИЧЕСКИЙ АНСАМБЛЬ, см. Микроканонический ансамбль Гиббса.

ГИББСА ПРАВИЛО ФАЗ (правило фаз), для любой термодинамически равновесной системы число парамет­ров состояния (v), к-рые можно из­менять, сохраняя число существую­щих фаз () неизмененным, опреде­ляется выражением: v=k+n-, где k — число компонентов системы, n — число параметров состояния системы, имеющих одно и то же значение во всех фазах (обычно темп-pa Т и дав­ление р). Величину v иногда наз. вариантностью системы. Правило фаз было выведено Дж. У. Гиббсом (1876) из условий термодинамического рав­новесия многокомпонентных систем. Правило справедливо при след. предположениях: 1) фазы имеют до­статочно большие размеры, так что поверхностными явлениями можно пре­небречь; 2) каждый компонент может проходить через поверхности раздела фаз (полупроницаемые перегородки отсутствуют). Если равновесное со­стояние системы определяется двумя параметрами (напр., Т и р), то v=k+2-. Значения v<0 не имеют физ. смысла, следовательно, k+2, т. е. число фаз, сосуществующих в равно­весии, не может превосходить числа независимых компонентов более чем на 2. При v=0 (безвариантная, или нонвариантная, система) равновесие имеет место при вполне определ. зна­чениях Т, р к составах каждой фазы. Условие v=0 определяет, следова­тельно, наибольшее возможное число фаз (_макс) в равновесной системе, составленной из определ. числа ком­понентов. Для k=1 (индивидуальное в-во, напр. вода) _макс=3 (в равно­весии могут находиться пар, лёд, вода, см. Тройная точка), для k=2 (бинарная система, напр. вода и соль) _макс=4 (соль, лёд, жидкий р-р, пар) и т. д. При v=1 (одновариантная, или моновариантная, система) одну из переменных, напр. Т, можно варьировать, тогда др. переменные (р, концентрации) в условиях равно­весия будут полностью определяться темп-рой.

Г. п. ф. применяется в металлове­дении, металлургии, петрографии, хим. технологии при исследовании много­компонентных гетерогенных систем, т. к. позволяет рассчитывать возмож­ное число фаз и степеней свободы в равновесных системах при любом чис­ле компонентов.

• Гиббс Дж. В., Термодинамические ра­боты, пер. с англ., М.— Л., 1950, с 143; Древинг В. П., Калашни­ков Я. А., Правило фаз с изложением ос­нов термодинамики, 2 изд., М., 1964, с. 133; Сторонкин А. В., Термодинамика ге­терогенных систем, ч. 1—3, Л., 1967—69; Карапетьянц М. X., Химическая тер­модинамика, 3 изд., М., 1975.

ГИББСА РАСПРЕДЕЛЕНИЯ, равно­весные распределения вероятностей состояний статистич. систем в разл. физ. условиях — фундам. законы статистич. физики, установленные Дж. У. Гиббсом (1901). Г. р. имеют место как для состояний классич. си­стем, полная энергия к-рых опреде­ляется Гамильтона функцией Н (р, q) в фазовом пр-ве координат q и им­пульсов р всех ч-ц системы, так и для квант. состояний систем, характери­зуемых уровнями энергии.

К энергетически изолированным от окружающей среды системам с энер­гией 8 при пост. объёме V и с задан­ным числом ч-ц N (микроканониче­ский ансамбль Гиббса) применимо микроканонич. распределение Гиббса

f(p,q)=A{H(p,q)-ξ},

где  — дельта-функция Дирака, А — постоянная, позволяющая определить энтропию системы как ф-цию ξ, V, N. Системы в контакте с термостатом, т. е. с перем. энергией, имеющие пост. объём и заданное число ч-ц (канони­ческий ансамбль Гиббса), описываются канонич. распределением Гиббса



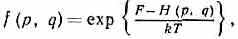
где F — свободная энергия (Гельм­гольца энергия) как ф-ция V, Т, N. Системы, имеющие пост. объём, при термич. и матер. контакте с термо­статом (т. н. Гиббса большой канони­ческий ансамбль) обладают перем. энергией и перем. числом ч-ц (за счёт обмена с термостатом энергией и в-вом) и описываются большим канонич. распределением Гиббса



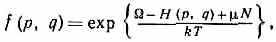
где , — химический потенциал,  — термодинамич. потенциал в перемен­ных V, Т, .

Системы в термич. и механич. кон­такте с окружающей средой, т. е. с переменными энергией и объёмом, но пост. давлением р (изобарически-изотермич. ансамбль Гиббса), описыва­ются изобарич. Г. р.



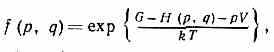
где G — Гиббса энергия.

Для квант. систем Г. р. имеют та­кую же форму, но вместо Н(р, q) в них стоит энергия квант. уровня системы ξ_i. Из условия, что полная вероятность пребывания системы в к.-л. из состояний равна единице (ус­ловие нормировки), определяются кон-

115


станты A, F, , G в Г. р., т. е. все потенциалы термодинамические (см. Статистическая физика). Для вы­числения термодинамич. ф-ций можно пользоваться любым Г. р., они в этом случае эквивалентны, несмотря на то что каждое Г. р. соответствует определ. физ. условиям.

Д. Н. Зубарев.