Агрегатное состояние в-ва, в к-ром его ч-цы не связаны или весьма слабо связаны силами вз-ствия и дви­жутся свободно, заполняя весь предо­ставленный им объём

Вид материала

Документы

Содержание Гармонические колебания Гартмана генератор Схема генера­тора Гартма­на Ю. Я. Борисов. ГАУССА ПРИНЦИП (принцип наи­меньшего принуждения) Z равняется сумме таких величин. Рассмотрим, напр., точку, к-рая на­чинает двигаться вдоль гладкой на­клонной плоскости из полож Гаусса система единиц Гаусса теорема Г. Я. Мякишев. ГЕЙГЕРА СЧЁТЧИК (Гейгера — Мюллера счётчик) Рис. 1. Счётчик Гейгера. Рис. 2. Схема регистрирующего устройства со счётчиком Гейгера N регистрируе­мых в ед. времени импульсов от при­ложенного к счётчику напряжения V Гей-люссака законы Гелий жидкий Рис. 1. Диаграмма состояния Рис. 2. Теплоёмкость Л. П. Питаевский. Э. А.Канер. Генератор измерительный ... Полное содержание

Подобный материал:

• 2. Молекулярно-кинетическая теория идеальных газов, 52.42kb.
• Магия и технология – за и против (или наоборот – вместе или порознь) Гилдор Карнесир, 243.69kb.
• Тема: Инновации и инновационные процессы, 158.08kb.
• Т. И. Розбицкая Музыка в жизни и творчестве И. С. Тургенева Все виды искусства так, 46.59kb.
• Ii этап Команда «исследователи» моу «сош №2», 94.86kb.
• 1 Использование ресурсов минерально-сырьевой базы края и охрана недр, 291.61kb.
• Позиционирования (gps), 196.2kb.
• Конспект тема: Бизнес план и его роль в современном предпринимательстве, 598.08kb.
• Задания для второго (районного, городского) этапа Всероссийской олимпиады школьников, 68.78kb.
• Курсовые работы на III и IV курсах обязательно должны быть связаны, 86.91kb.

ГАРМОНИКА, см. Обертон.

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ, колебания, при к-рых физ. (или любая другая) величина изменяется с тече­нием времени по синусоидальному за­кону: x=Asin(t+), где x — значе­ние колеблющейся величины в данный



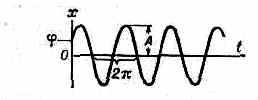
момент времени t (для механич. Г. к., напр., смещение или скорость, для электрич. Г. к.— напряжение или си­ла тока), А — амплитуда колебаний,  — угл. частота колебаний (t+) — фаза колебаний,  — нач. фаза колебаний.

Г. к. занимают среди всех колебаний особое место, так как Г. к.— единств. тип колебаний, форма к-рых не иска­жается при прохождении через любую линейную систему. Кроме того, любое негармонич. колебание можно пред­ставить в виде суммы разл. Г. к., т. е. в виде спектра гармонич. колебаний.

• См. лит. при ст. Колебания.

ГАРТМАНА ГЕНЕРАТОР, газоструй­ный излучатель высокого давления звук. и ультразвук. волн. Назван по имени изобретателя — дат. учёного Ю. Гартмана (J. Hartmann; 1922).

Осн. часть Г. г.— сопло 1 (рис.), откуда вытекает сверхзвук. газовая струя, в к-рой возникают волны уп­лотнения и разрежения. Если соосно с соплом поместить на нек-ром расстоя­нии резонатор 2, то при торможении струи перед резонатором возникает отсоединённый скачок уплотнения 3. В результате вз-ствия осн. струи и струи, вытекающей из резонатора, при определ. расстоянии между соплом и резонатором участок струи за скачком становится источником звук. и ультра­звук. волн.



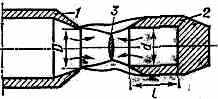
Схема генера­тора Гартма­на.


Частота излучаемого зву­ка зависит от расстояния между соплом и резонатором, а также от размера ре­зонатора. Наиболее благоприятные ус­ловия излучения имеют место, когда диаметр D выходного отверстия сопла и длина l резонатора равны между со­бой, а диаметр d полости резонатора в 1,3—1,5 раза превышает диаметр сопла.

Мощность акустич. излучения Г. г. достигает неск. десятков Вт, а кпд — 3—5%. При использовании сжатого воздуха получают частоты от 1—2 до 60 кГц. Применяя вместо воздуха во­дород, можно получить частоты до 180 кГц.

• Источники мощного ультразвука, М., 1967 (Физика и техника мощного ультразву­ка, под ред. Л. Д. Розенберга, кн. 1).

Ю. Я. Борисов.

ГАУСС (Гс, Gs), единица магн. индук­ции в СГС системе единиц (симметрич­ной, или Гауссовой) и СГСМ. Названа в честь нем. учёного К. Ф. Гаусса (К. F. Gau8). 1 Гс=10^-4 тесла.

ГАУССА ПРИНЦИП (принцип наи­меньшего принуждения), один из ва­риационных принципов механики, со­гласно к-рому для механич. системы с идеальными связями (см. Связи меха­нические) из всех кинематически воз­можных, т. е. допускаемых связями, движений, начинающихся из данного положения и с данными нач. скоростя­ми, истинным будет то движение, для к-рого «принуждение» Z явл. в каждый момент времени наименьшим. Установ­лен нем. учёным К. Ф. Гауссом (1829). Физ. величина, наз. «принуждени­ем», вводится след. образом. Свободная матер. точка с массой m при действии на неё заданной силы F будет иметь ускорение F/m; если же на точку на­ложены связи, то её ускорение при действии той же силы станет равным какой-то др. величине w. Тогда откло­нение точки от свободного движения, вызванное действием связи, будет за­висеть от разности этих ускорений, т. е. от F/m-w. Величину Z, пропорц. квадрату этой разности, и наз. «при­нуждением». Для одной точки

Z=¹/₂m(F/m-w)².

а для механич. системы Z равняется сумме таких величин.

Рассмотрим, напр., точку, к-рая на­чинает двигаться вдоль гладкой на­клонной плоскости из положения А без нач. скорости (рис.).



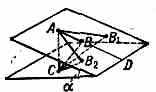
Для неё ки­нематически возможно любое переме­щение АВ, АВ₁, АВ₂,... в этой плоско­сти с какими-то ускорениями w, w₁, w₂,...; при свобод­ном же падении точ­ка совершила бы пе­ремещение вдоль вертикали АС с ус­корением g. Тогда отклонения точки от свободного движе­ния изобразятся отрезками СВ, СВ₁, СВ₂, . . ., наименьшим из к-рых будет отрезок СВ, перпендикулярный к на­клонной плоскости. Следовательно, «принуждение» Z, пропорц. квадратам СВ, СВ₁, СВ₂, . . . , будет наимень­шим при движении вдоль линии наи­меньшего ската AD. Это и будет ис­тинное движение точки, происходящее с ускорением w=gsin. Математиче­ски Г. п. выражается равенством Z=0, в к-ром варьируются только уско­рения точек системы; при этом пред­полагается, что силы от ускорения не зависят.

Г. п. пользуются для составления ур-ний движения механич. систем и изучения св-в этих движений.

• См. лит. при ст. Вариационные принципы механики.

С. М. Тарг,

ГАУССА СИСТЕМА ЕДИНИЦ, си­стема единиц электрич. и магн. вели­чин с осн. единицами сантиметр, грамм, секунда, в к-рой диэлектрич. () и магн. () проницаемости явл. безраз­мерными величинами, причём для ва­куума =1 и =1. Ед. электрич. ве­личин в Г. с. е. равны единицам абс. электростатич. системы СГСЭ, а ед. магн. величин — единицам эл.-магн. системы СГСМ, в связи с чем Г. с. е. часто наз. симметричной сис­темой СГС (см. СГС система единиц). Г. с. е. названа в честь нем. учёного К. Ф. Гаусса, впервые в 1832 пред­ложившего абсолютную систему еди­ниц с осн. ед.: миллиметр, миллиграмм и секунда, и применившего эту систе­му для измерений магн. величин.

• Б у р д у н Г. Д., Единицы физических величин, 4 изд., М., 1967.

ГАУССА ТЕОРЕМА, основная теорема электростатики, устанавливающая связь потока напряжённости Е электрич. поля через замкнутую поверх­ность S с величиной заряда q, находя­щегося внутри этой поверхности. В Га­усса системе единиц

divE=4q. (1)

Г. т. вытекает из Кулона закона.

В диэлектрике Г. т. справедлива для потока вектора электрич. индукции D:

divD=4q, (2)

где q — суммарный свободный заряд внутри поверхности S. Ф-ла (2) представляет собой интегр. форму од­ного (4-го) из Максвелла уравнений для эл.-магн. поля и выражает тот


110


факт, что электрич. заряды явл. ис­точниками электрич. поля.

Г. Я. Мякишев.

ГАЮИ ЗАКОН (закон рациональных отношений), эмпирич. закон огранения кристаллов, установленный франц. кристаллографом Р. Ж. Гаюи (Аюи, R. J. Hauy) в 1784. Если за коорди­натные оси OX, OY, OZ выбрать нек-рые рёбра кристалла, то взаимные наклоны граней кристалла таковы, что отрезки, отсекаемые ими на осях координат, относятся как целые числа l, m, n, т. е. могут быть выражены как кратные некоторых осевых единиц а, b, с (рис.).



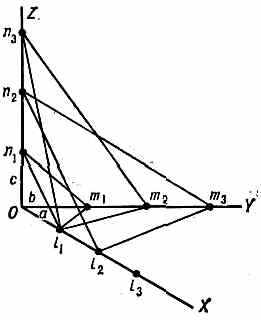
Наличие осе­вых единиц и привело к выводу о трёхмерной периодичности строения кристаллов, т. е. о существовании кристаллической решётки. Грани кристалла соответствуют ат. пло­скостям решётки, а рёбра — её рядам, осевые ед.— постоянным решётки.

• См. лит. при ст. Кристаллография.

ГЕЙГЕРА СЧЁТЧИК (Гейгера — Мюллера счётчик), газоразрядный де­тектор, срабатывающий при прохож­дении через его объём заряж. ч-ц. Величина сигнала (импульса тока) не зависит от энергии ч-ц (прибор рабо­тает в режиме самостоят. разряда). Г. с. изобретён в 1908 нем. физиком X. Гейгером совместно с англ. физи­ком Э. Резерфордом, затем усовершен­ствован Гейгером и нем. физиком В. Мюллером. Г. с. сыграли важную роль в яд. физике в 20—40 гг. Они продолжают применяться, в частно­сти, в дозиметрии.



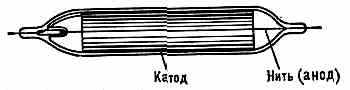
Рис. 1. Счётчик Гейгера.


В Г. с. рабочий объём — газораз­рядный промежуток с сильно неодно­родным электрич. полем. Чаще всего применяют коаксиальные цилиндрич. электроды; внеш. цилиндр — катод, тонкая нить, натянутая вдоль его оси, анод (рис. 1). Электроды заключены в герметич. резервуар, наполненный га­зом до давления 100—200 мм рт. ст.



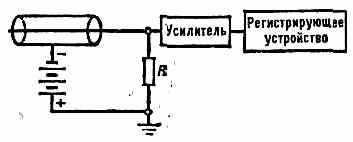
Рис. 2. Схема регистрирующего устройства со счётчиком Гейгера.


К электродам прикладывается напря­жение в неск. сотен вольт. При попа­дании ионизирующей ч-цы в резервуар в газе образуются свободные эл-ны, к-рые движутся к нити. Вблизи нити напряжённость электрич. поля вели­ка, и эл-ны ускоряются настолько, что начинают в свою очередь ионизовать газ. По мере приближения к нити чис­ло эл-нов лавинообразно нарастает. Возникает коронный разряд, распро­страняющийся вдоль нити. Этот раз­ряд обрывается включением большого сопротивления R~10⁸—10⁹ Ом (несамогасящийся Г. с., рис. 2) либо с введением спец. состава газовой смеси инертного газа с примесью паров спирта или др. многоат. газа и галоге­нов (с а м о г а с я щ и й с я Г. с.). Временное разрешение самогасящихся Г. с. ~10^-6 с. Время восстановления их чувствительности определяется вре­менем дрейфа ионов к катоду и состав­ляет ок. 10^-4 с.

Электрич. импульсы во внеш. цепи, возникающие при вспышках разряда в Г. с., усиливаются и регистрируют­ся. Зависимость числа N регистрируе­мых в ед. времени импульсов от при­ложенного к счётчику напряжения V



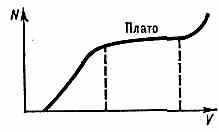
Рис. 3. Счётная хар-ка счётчика Гейгера.

наз. счётной хар-кой Г. с. (рис. 3). Рабочий участок хар-ки (плато) имеет протяжённость от неск. десятков вольт до неск. сотен вольт. На плато число отсчётов практически равно числу ионизирующих ч-ц, попадающих в счётчик. Гамма-кванты регистриру­ются по вторичным заряж. ч-цам — фотоэлектронам, комптоновским эл-нам, электронно-позитронным па­рам (см. Гамма-излучение); нейтро­ны — по ядрам отдачи и продуктам яд. реакций, возникающих в газе счёт­чика.

•См. лит. при ст. Детекторы.

ГЕЙ-ЛЮССАКА ЗАКОНЫ, 1) один из осн. газовых законов, согласно к-рому объём данной массы газа при пост. давлении меняется линейно с темп-рой: V_t=V₀(1+_Vt), где V₀ и V_t — объёмы газа при нач. и кон. темп-рах, t — разность этих темп-р, _V — коэфф. теплового расширения газов при пост. давлении, примерно равный для всех газов 1/273,15 К^-1. Г.-Л. з. строго

справедлив для идеальных газов; реальные газы подчиняются ему при темп-рах и давлениях, далёких от критич. значений. Является частным слу­чаем Клапейрона уравнения. Открыт франц. учёным Ж. Л. Гей-Люссаком (J. L. Gay-Lussac) в 1802.

2) Закон, утверждающий, что объ­ёмы газов, вступающих в хим. реак­ции, находятся в простых отношениях друг к другу и к объёмам газообразных продуктов реакции, т. е. в отношениях небольших целых чисел, напр. 1:1:2 (закон объёмных отношений). Открыт Ж. Л. Гей-Люссаком в 1808. Сыграл большую роль в открытии Авогадро закона.

ГЕКТО... (от греч. hekaton — сто), приставка к наименованию ед. физ. величины для образования наимено­вания кратной единицы, равной 100 исходным ед. Обозначения: Г, h. При­мер: 1 гВт (гектоватт)=100 Вт.

ГЕЛИЙ ЖИДКИЙ, бесцветная проз­рачная жидкость, кипящая при атм, давлении и темп-ре 4,44 К (жидкий ⁴Не). Плотность жидкого ⁴Не при 4,2 К~0,13 г/см³, под давлением насыщ. паров он остаётся жидким при всех темп-pax ниже критической T_к=5,20 К. Затвердевает ⁴Не лишь при давлениях, больших 25 атм (рис. 1). Согласно квант. механике, это объяс­няется тем, что даже при абс. нуле ато­мы в Г. ж. движутся (испытывают «ну­левые колебания»), что препятствует затвердеванию жидкости (см. Кванто­вая жидкость). Кроме изотопа ⁴Не в природе существует ещё один устой­чивый, но редкий изотоп гелия ³Не (на него приходится ~10^-7% общей массы гелия, находящегося в воздухе).



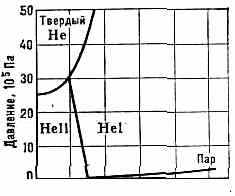
Рис. 1. Диаграмма состояния ⁴Не.


Критич. темп-pa ³Не равна 3,35 К, критич. плотность 0,064 г/см³. При норм. давлении ³Не, как и ⁴Не, неза­мерзающая жидкость, она затверде­вает лишь при давлениях 30 атм. При темп-ре Т_=2,17 К и давлении насыщ. паров ⁴Не испытывает фазовый переход II рода. Гелий выше этой темп-ры наз. Не I, ниже — Не II. При темп-ре фазового перехода наблю­даются аномалия теплоёмкости (-точка, рис. 2), излом кривой темпера­турной зависимости плотности Г. ж. (рис. 3). Не I резко отличается по внеш. виду от Не II: первый бурно

111


кипит во всём объёме, а Не II — спо­койная жидкость с отчётливой по­верхностью. Объясняется это необы­чайно высокой теплопроводностью Не II, во много млн. раз превосходя­щей теплопроводность Не I, равную~10^-5 кал/(К•см•с), или 4,2•10^-5 Дж/(К•м•с).



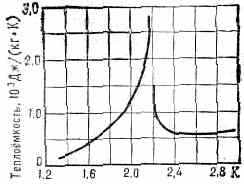
Рис. 2. Теплоёмкость ⁴Не вблизи темп-ры Т_=2,19К (-точки) при атм. давлении.


В 1938 П. Л. Капица открыл у Не II сверхтекучесть. Объяснение это­го явления было дано Л. Д. Ландау (1941) на основе кпантовомеханич. представлений о хар-ре теплового дви­жения в Г. ж. Тепловое движение в Не II при темп-pax, близких к абс. нулю, описывается как существование



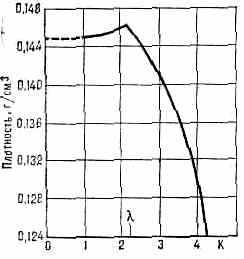
Рис. 3. Плотность  ⁴Не вблизи -точки.


в Г. ж. элем. возбуждений (квазичас­тиц) — фононов, обладающих энер­гией =hv (v — частота колебаний) и импульсом р=/с (с — скорость звука=240 м/с). Число и энергия фононов растут с повышением Т. При Т0,6 К появляются возбуждения с большими энергиями (ротоны), для к-рых зависимость (р) имеет нели­нейный хар-р. Фононы и ротоны дви­жутся в Г. ж. подобно ч-цам газа. Они обладают импульсом и, следова­тельно, массой (см. Эффективная мас­са). Отнесённая к 1 см³, эта масса опре­деляет плотность _n т. н. н о р м а л ь н о й компоненты Г. ж. При T_n=2²(kT)⁴/(45h³с⁵), она стре­мится к нулю при Т 0.

Движение норм. компоненты, как и обычного газа, имеет вязкостный хар-р. Остальная часть Г. ж., т. н. с в е р х т е к у ч а я компонента, движется без трения; её плотность _s=-_n. При TT_ _n, так что в Ls-точке _s обращается в нуль и

сверхтекучесть исчезает (Не I — обыч­ная вязкая жидкость). Т. о., при T в Г. ж. одновременно могут про­исходить два движения с разл. ско­ростями (двухкомпонентная модель Ландау).

Двухкомпонентность Не II позво­ляет объяснить ряд наблюдаемых эф­фектов: при вытекании Не II из сосуда через узкий капилляр темп-pa в сосуде повышается, т. к. вытекает гл. обр. сверхтекучая компонента, не несущая с собой теплоты (т. н. м е х а н о к а л о р и ч е с к и й эффект); при создании разности темп-р между кон­цами закрытого капилляра с Не II в нём возникает движение — сверхтеку­чая компонента движется от холодного конца к горячему и там превращается в нормальную, к-рая движется на­встречу, при этом суммарный поток отсутствует (т е р м о м е х а н и ч е с к и й э ф ф е к т). В Г. ж. наряду с обычным звуком может распростра­няться т. н. второй звук. Св-ва Г. ж. ³Не существенно отличаются от св-в жидкого ⁴Не, что связано не только с различием масс атомов ⁴Не и ³Не, но и с их квантовомеханич. особенностями (атомы ⁴Не — бозоны, атомы ³Не — фермионы). Сверхтекучим ³Не стано­вится при очень низкой темп-ре (~2,6 мК) под давлением ~34 атм. У ³Не существует две сверхтекучие фазы: анизотропная (фаза А) и изо­тропная (фаза В). Переход обычного ³Не в фазу ³Не-A относится к фазо­вым переходам II рода, а переход ³Не-A  ³Не-B — к фазовым перехо­дам I рода (возможны эффекты пере­грева и переохлаждения). А-фаза су­ществует в температурном интервале 2,6—2 мК, фаза В — при 72 мК (температурные границы существенно зависят от давления).

Большим разнообразием св-в обла­дают р-ры жидких ⁴Не и ³Не (особенно сверхтекучие р-ры ³Не — Не II).

• К е е з о м В., Гелий, пер. с англ., М., 1949; Халатников И. М., Теория сверх­текучести, М., 1971.

Л. П. Питаевский.

ГЕЛИКОН (от греч. helix, род. п. helikos — кольцо, спираль) (спираль­ная волна), низкочастотная эл.-магн. волна, возникающая и распространяю­щаяся с относительно слабым затуха­нием в проводниках (металлах, полу­проводниках, плазме), помещённых в пост. магн. поле Н. Г. аналогичен сви­стящим атмосферикам, распростра­няющимся в газовой и ионосферной плазме. Г. возникают в проводниках с разными концентрациями носителей тока (напр., эл-нов проводимости n₁ и дырок n₂) в результате Холла эф­фекта. Зависимость частоты  Г. от его длины волны  имеет вид:



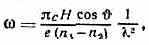
где е — заряд эл-на, - — угол между направлением распространения волны и магн. полем. Г. эллиптически поля­ризован в плоскости, перпендикуляр­ной Н, и его электрич. вектор Е вра­щается вокруг Н в том же направлении, что и избыточная часть носителей заряда.

Г. образуются в сильных магн. по­лях, когда радиус орбиты носителей R<длина свободного пробега носителей), а частота  мала по срав­нению с циклотронной частотой. Г. не распространяются в направлении, перпендикулярном Н. Затухание Г. обусловлено столкновениями носите­лей заряда с фононами и дефектами крист. решётки, а также бесстолкновительным резонансным поглощением (магн. затухание Ландау). В чистых металлах при низких темп-pax осн. роль играет резонансное поглощение, в ПП — столкновения.

• К а н е р Э. А., С к о б о в В. Г., Эле­ктромагнитные волны в металлах в магнит­ном поле, «УФН», 1966, т. 89, в. 3, с. 367,

Э. А.Канер.

гельмгольца резонатор же, что резонатор акустический.

ГЕЛЬМГОЛЬЦА ЭНЕРГИЯ (свобод­ная энергия), один из потенциалов термодинамических; характеристиче­ская функция термодинамич. системы при независимых параметрах V (объём) и Т (термодинамич. темп-pa); обозна­чается F (иногда А), определяется че­рез внутреннюю энергию U, энтропию S и темп-ру Т равенством: F= U-TS. Понятие «Г. э.» (свободная энергия) введено нем. физиком Г. Гельмгольцем (Н. Helmholtz; 1882). В изотерми­ческом равновесном процессе, происхо­дящем при постоянном объёме, убыль Г. э. системы равна полной работе, производимой системой в этом про­цессе. Г. э. выражается обычно в кДж/моль или кДж/кг.

ГЕНЕРАТОР ИЗМЕРИТЕЛЬНЫЙ, мера, воспроизводящая дискретный или непрерывный ряд значений пара­метров перем. электрич. величины (на­пряжения, тока) в определ. диапазоне. Применяется в измерит. практике, а также для поверки и регулировки радиотехнических и вычислительных устройств, устройств автоматики и др.

В зависимости от формы воспроиз­водимых сигналов различают Г. п.: гармонич. сигналов; импульсов прямоуг. формы; сигналов спец. формы (треугольной, пилообразной, колоколообразной и др.); качающейся часто­ты (свип-генераторы, воспроизводящие гармонич. колебания, частота к-рых изменяется по определ. закону при неизменной амплитуде или мощности колебаний); шумовых сигналов, вос­производящих случайные электрич. колебания с определ. вероятностными хар-ками (дисперсией, корреляц. ф-цией и др.). В зависимости от частотного диапазона различают Г. и.: инфранизкочастотные (10^-3—20 Гц), низкочас­тотные (20 Гц — 200 кГц), высокочас­тотные (30 кГц — 30 МГц), СВЧ с ко­аксиальным выходом (30 МГц — 10 ГГц), СВЧ с волн. выходом (10— 80 ГГц).

Осн. частями практически всех ви­дов Г. и. явл.: задающий гене­ратор — первичный электронный ис-

112


точник гармонич. колебаний или пе­риодически повторяющихся импульсов с плавной регулировкой частоты; у с и л и т е л ь м о щ н о с т и, выпол­няющий также в Г. и. сигналов спец. формы ф-цию формирующего устрой­ства; в ы х о д н о е у с т р о й с т в о, при помощи к-рого регулируется амплитуда колебаний и осуществляет­ся согласование выходных цепей гене­ратора с нагрузкой; устройства контроля выходных сигналов Г. и. (электронный вольтметр для из­мерения амплитуды колебаний, изме­ритель мощности и др.). Г. и. высоких и сверхвысоких частот, как правило, снабжаются модулирующими устройствами, позволяющими изменять по определ. закону к.-л. из параметров гармонич. или импульс­ных сигналов (амплитуду, частоту и др.). Особую группу Г. и. составля­ют т. н. с и н т е з а т о р ы ч а с т о т ы — Г. и. гармонич. колебаний, вос­производящие с высокой стабильно­стью ряд частот с дискретностью до сотых долей Гц.

Промышленностью выпускается ши­рокая гамма Г. и. с относит. погреш­ностью установки частоты ~0,1— 1%, стабильностью частоты до 10^-6% за сутки (синтезаторы частоты), коэфф. гармоник до 0,1%, выходной мощ­ностью 10^-15—10 Вт, мин. длитель­ностью импульсов до 10 нс.

Требования к Г. и. стандартизованы в ГОСТах 9788-78 и 23767-79 (общие требования), 10501-74 (низкочастот­ные Г. и.), 14126-78 (Г. и. с коаксиаль­ным выходом), 17193-71 (Г. и. с вол­новым выходом), 11113-74 (Г. и. импульсов).

•Мирский Г. Я., Радиоэлектронные измерения, 3 изд., М., 1975;О сипов К. Д., Пасынков В. В., Справочник по радио­измерительным приборам, ч. 2, 5, М., 1960— 1964.

В. П. Кузнецов.