Агрегатное состояние в-ва, в к-ром его ч-цы не связаны или весьма слабо связаны силами вз-ствия и дви­жутся свободно, заполняя весь предо­ставленный им объём

Вид материала

Документы

Содержание СГС система единиц Грасгофа число Точечная группа сим­метрии ГРАФИЧЕСКАЯ СТАТИКА (графостатика) Громкость звука Кривые равной громкости — зависимость уровня звук. давления (в дБ) от частоты при заданной громкости (в фонах). Групповая скорость Рис. 1. Волновой пакет. Рис. 2. Последовательные моментальные снимки группы волн в моменты времени t М. А. Миллер, Е. В. Суворов. Грюнайзена закон Гука закон Гюгоньо адиабата Гюйгенса окуляр

Подобный материал:

• 2. Молекулярно-кинетическая теория идеальных газов, 52.42kb.
• Магия и технология – за и против (или наоборот – вместе или порознь) Гилдор Карнесир, 243.69kb.
• Тема: Инновации и инновационные процессы, 158.08kb.
• Т. И. Розбицкая Музыка в жизни и творчестве И. С. Тургенева Все виды искусства так, 46.59kb.
• Ii этап Команда «исследователи» моу «сош №2», 94.86kb.
• 1 Использование ресурсов минерально-сырьевой базы края и охрана недр, 291.61kb.
• Позиционирования (gps), 196.2kb.
• Конспект тема: Бизнес план и его роль в современном предпринимательстве, 598.08kb.
• Задания для второго (районного, городского) этапа Всероссийской олимпиады школьников, 68.78kb.
• Курсовые работы на III и IV курсах обязательно должны быть связаны, 86.91kb.

ГРАДУС угловой, единица плоского угла, равна ¹/₉₀ части прямого угла, обозначается °. 1°=60'= 3600", где ' — обозначение угл. минуты, " — угл. секунды. В Г. измеряют также дуги окружности (полная окружность равна 360°).

ГРАММ (франц. gramme, от лат. и греч. gramma — мелкая мера веса), основная ед. массы в СГС система единиц и дольная ед. СИ (0,001 кг). 1 г с точностью до 0,2% равен массе 1 см³ химически чистой воды при темп-ре её наибольшей плотности (ок. 4°С).

ГРАММ-ATOM, выходящее из употре­бления наименование ед. кол-ва в-ва, индивидуальной для каждого конкрет­ного в-ва. 1 Г.-а.— кол-во в-ва (хим. элемента), масса к-рого в граммах равна его ат. массе. В СИ осн. ед. количества в-ва — моль.

ГРАММ-МОЛЕКУЛА, устаревшее на­именование ед. количества в-ва — моля.

ГРАСГОФА ЧИСЛО [по имени нем. учёного и инженера Ф. Грасгофа (Грасхоф, F. Grashof)], подобия крите­рий, определяющий перенос теплоты для случая свободной конвекции, когда движение среды происходит под дей­ствием силы тяжести и вызывается разностью плотностей из-за неравно­мерности поля темп-р, Г. ч.



где g — ускорение свободного паде­ния, l — характерный размер, v — коэфф. кинематич. вязкости,  — коэфф. объёмного расширения, Т — разница темп-р между поверхностью тела и средой или разл. слоями среды. Г. ч. явл. произведением числа gTl²/v характеризующего отноше­ние силы трения к подъёмной (архи­медовой) силе, на Рейнольдса число Re=vl/hv, где v — скорость течения жидкости или газа.

ГРАФИТ (нем. Graphit, от греч. grapho — пишу), природный и синтетич. кристалл углерода, устойчивый при норм. условиях. Точечная группа сим­метрии 6/mmm, плотность 2,23 г/см³, T_пл=3850±50°С. Кислотоупорен (оки­сляется только при высоких темп-рах), жаропрочен, легко обрабатывается, хорошо проводит электрич. ток. Обладает малым сечением захвата теп­ловых нейтронов, малым коэфф. тре­ния, резкой анизотропией св-в: твёр­дость вдоль оси 6 по шкале Мооса — 1, перпендикулярно этой оси — 5,5 и выше; коэфф. теплового расширения а вдоль оси 6 равен 28,2•10^-6 К^-1, перпендикулярно этой оси: 1,5X10^-6 К^-1. При облучении нейтро­нами увеличиваются твёрдость, элек­тросопротивление, модуль упругости,

а теплопроводность уменьшается (в 20 раз). Синтетич. Г. применяется в кач-ве эррозионностойких покрытий для сопел ракетных двигателей, ка­мер сгорания, для изготовления отд. деталей ракет, в электротехнике и хим. промышленности, а также в кач-ве замедлителя нейтронов в ядер­ных реакторах.

ГРАФИЧЕСКАЯ СТАТИКА (графостатика), учение о графич. методах решения задач статики. Методами Г. с. путём соответствующих геом. построений могут определяться ис­комые силы, изгибающие моменты, центры тяжести и моменты инерции плоских фигур и др. С использова­нием Д'Аламбера принципа методы Г. с. могут применяться к решению задач динамики. Г. с. пользуются в строит. механике при расчётах балок, ферм и др. конструкций, а также при расчётах усилий в разл. деталях ме­ханизмов и машин. По точности рас­чётов методы Г. с. значительно усту­пают аналитическим (численным) ме­тодам.

• См. лит. при ст. Статика.

ГРОМКОСТЬ ЗВУКА, величина, ха­рактеризующая слуховое ощущение для данного звука. Г. з. сложным об­разом зависит от звукового давления (или интенсивности звука), частоты и формы колебаний. При неизменной частоте и форме колебаний Г. з. ра­стёт с увеличением звук. давления



Кривые равной громкости — зависимость уровня звук. давления (в дБ) от частоты при заданной громкости (в фонах).


(рис.). При одинаковом звук. давле­нии Г. з. чистых тонов (гармонич. колебаний) разл. частоты различна, т. е. на разных частотах одинаковую громкость могут иметь звуки разной интенсивности. Г. з. данной частоты оценивают, сравнивая её с громкостью чистого тона частотой 1000 Гц. Уро­вень звук. давления (в дБ) чистого тона с частотой 1000 Гц, столь же громкого (сравнением на слух), как и измеряемый звук, наз. уровнем гром­кости данного звука (в фонах).

ГРУППОВАЯ СКОРОСТЬ, скорость движения группы или цуга волн, об­разующих в каждый данный момент времени локализованный в пр-ве волновой пакет (рис. 1). В линейных средах, где соблюдается суперпозиции принцип, его можно рассматривать

138


как набор гармонич. волн с частотами в интервале ₀-<<₀+ тем более узком, чем плавнее и протяжён­нее огибающая группы. Длина пакета L и его спектр. полоса  ограниче­ны снизу соотношением Lk1, где волновое число k связано с частотой со дисперсионным соотношением =(k) (см. Дисперсия волн).

Если среда не обладает дисперси­ей, то все гармонич. волны распро­страняются с одной и той же фазовой



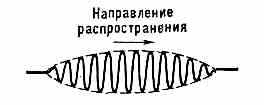
Рис. 1. Волновой пакет.


скоростью и пакет ведёт себя как строго стационарная волна — его Г. с. совпадает с фазовой скоростью. При наличии дисперсии волны разл. ча­стот распространяются с разными фа­зовыми скоростями и форма огибаю­щей искажается. Однако для сигна­лов с достаточно узким спектром, когда фазовые скорости гармонич. волн, образующих волн. пакет, мало отличаются друг от друга, и на не слишком больших расстояниях, когда форма огибающей приближённо со­храняется, влияние дисперсии сказы­вается лишь на скорости перемещения



Рис. 2. Последовательные моментальные снимки группы волн в моменты времени t₁, t₂, t₃: a — в случае нормальной дисперсии; б — в случае аномальной дисперсии.


огибающей, к-рая и есть Г. с. Посколь­ку распространение двух синусои­дальных волн с близкими частотами ₀+ пакета описывается выраже­ниями

sin[(₀±)t-(k₀±k)x],

то скорость их огибающей равна /k, что в пределе приводит к ф-ле: v_гр=д(/дk│_k0.

На рис. 2 представлены три после­довательных мгновенных снимка сиг­нала с узким спектром, распростра­няющегося в среде с дисперсией. Нак­лон пунктирных прямых, соединяю­щих точки одинаковой фазы, харак­теризует фазовую скорость; наклон прямых, соединяющих соответствую­щие точки огибающей (начала и концы сигнала), характеризует Г. с. сигнала. Если при распространении сигнала максимумы и минимумы движутся быстрее, чем огибающая, то это озна­чает, что фазовая скорость данной

группы волн превышает её Г. с. (рис. 2, а). При распространении сиг­нала в его «хвостовой» части возни­кают всё новые максимумы, к-рые постепенно перемещаются вперёд вдоль сигнала, достигают его «головной» части и там исчезают. Такое положе­ние имеет место в случае т. н. норм. дисперсии, т. е. в средах, где показа­тель преломления n увеличивается с ростом частоты гармонической волны (dn/d>0). Такую дисперсию наз. так­же отрицательной, поскольку с ростом k фазовая скорость v_ф волны убывает. Примеры сред с норм. дисперсией — в-ва, прозрачные для оптич. волн, вол­новоды, изотропная плазма и др. Од­нако в ряде случаев наблюдается ано­мальная (положительная) дисперсия среды (dn/d<0); в этих случаях Г. с. сигнала превышает v_ф(д/дk>/k). Максимумы и минимумы появляют­ся в передней части группы (рис. 2, 6), перемещаются назад и исче­зают в «хвосте» сигнала. Аномаль­ная дисперсия характерна для капил­лярных волн на поверхности воды v_гр=2v_ф), для эл.-магн. и акустич. волн в средах с резонансным погло­щением, а также (при определ. усло­виях) для волн в периодич. структу­рах (кристаллы, замедляющие струк­туры и т. п.). При этом возможна даже ситуация, при к-рой Г. с. на­правлена противоположно фазовой. Понятие Г. с. играет важную роль и в физике и в технике, поскольку все методы измерения скоростей рас­пространения волн, связанные с за­паздыванием сигналов (в т. ч. ско­рости света), дают Г. с. Именно она фигурирует при измерении дальности в гидро- и радиолокации, при зондиро­вании ионосферы, в системах управ­ления косм. объектами и т. д. Соглас­но относительности теории, всегда vгрc, где c — скорость света в ва­кууме; для фазовых скоростей огра­ничений не существует.

• Горелик Г. С., Колебания и волны, 2 изд., М., 1959; П и р с Дж., Почти все о волнах, пер. с англ., М., 1976; К р а у ф о р д Ф., Волны, пер. с англ., 2 изд., М., 1976 (Берклеевский курс физики, т. 3).

М. А. Миллер, Е. В. Суворов.

ГРЭЙ (Гр, Gy), единица СИ погло­щённой дозы ионизирующего излу­чения и кермы. Названа в честь англ. учёного Л. Грэя (Грей, L. Gray). 1 Гр равен дозе излучения, при к-рой облучённому в-ву массой 1 кг передаётся энергия любого ионизи­рующего излучения 1 Дж. 1 Гр=1 Дж/кг=10⁴ эрг/г=10² рад. ГРЮНАЙЗЕНА ЗАКОН, устанавли­вает, что отношение коэфф. теплового расширения а к теплоёмкости С_V тв. тела (при пост. объёме) не зависит от темп-ры. Для кристаллов с простыми крист. решётками (для большинства элементов и ряда простых соединений, напр. галогенидов):

/C_V=_ДVd_Д/dp,

где _Д — Дебая температура, V — объём тела, р — давление. Установлен эмпирически в 1908 нем. физиком Э. Грюнайзеном (Е. Gruneisen).

ГУКА ЗАКОН, выражает линейную зависимость между напряжениями и малыми деформациями в упругой сре­де. В 1660 англ. учёный Р. Гук (R. Ноoke) обнаружил, что при растяжении стержня длиной l и площадью попе­речного сечения S удлинение стерж­ня l пропорц. растягивающей силе F, т. е. l=kF, где k=l/ES (Е — модуль Юнга). Г. з. можно предста­вить в виде: =Е, где =F/S — норм. напряжение в поперечном се­чении, =l/l — относит. удлинение стержня. При сдвиге касат. напряже­ние  пропорц. деформации сдвига у, т. е. =G, где G — модуль сдвига.

В сложном напряжённом состоянии изотропного упругого тела шесть ком­понентов тензора напряжений _ij свя­заны с шестью компонентами тензора деформации _ij обобщённым Г. з.: ₁₁=+2₁₁, ₂₂=+2₂₂, . . ., ₃₁=2₃₁, где =₁₁+₂₂+₃₃ — относит. изменение объёма,  и  — постоянные Ламе. Следовательно, упругие св-ва изотропного материа­ла определяются двумя константа­ми  и , через к-рые выражаются др. модули упругости.

В анизотропном материале обобщён­ный Г. з. имеет вид:



причём из 36 модулей упругости С_ij в общем случае анизотропии незави­симы 21. Г. з. справедлив для боль­шинства тв. тел при малых деформа­циях и явл. основным физ. законом упругости теории.

• Ильюшин А. А., Ленский В. С., Сопротивление материалов, М., 1959; Т и м о ш е н к о С. П., Гудьер Дж., Теория упругости, пер. с англ., 2 изд., М., 1979.

В. С. Ленский.

ГЮГОНЬО АДИАБАТА, кривая, оп­ределяемая Гюгоньо ур-нием. См. Ударная волна.

ГЮГОНЬО УРАВНЕНИЕ [по имени франц. учёного П. А. Гюгоньо (P. H. Hugoniot)], уравнение, свя­зывающее плотность и давление в потоке газа перед фронтом ударной волны с плотностью и давлением газа за волной. Кривая, изображающая Г. у., наз. адиабатой Гюго­ньо (см. Ударная волна). Г. у. при­меняется в газовой динамике, а также в теории взрыва и детонации.

ГЮЙГЕНСА ОКУЛЯР, см. Окуляр.

ГЮЙГЕНСА — ФРЕНЕЛЯ ПРИН­ЦИП, приближённый метод решения задач о распространении волн, осо­бенно световых. Согласно этому прин­ципу, первоначально введённому голл. учёным X. Гюйгенсом (Ch. Huygens; 1678), каждый элемент поверхности, к-рой достигла в данный момент вол­на, явл. центром элем. волн, огибаю­щая к-рых будет волн. поверхностью в следующий момент времени (рис. 1);

139




. обратные элем. волны (пунктирные линии) во внимание не принимаются. Этот принцип упрощает задачу опре­деления влияния всего волн. процес­са, совершающегося в нек-ром объё­ме, на к.-л. точку, сведя её к вычислению действия на данную точку про­извольно выбранной волн. поверх­ности. Принцип Гюйгенса объясняет распространение волн, согласующееся с законами геометрической оптики, но не объясняет явлений дифракции. Франц. физик О. Ж. Френель (A. J. Fresnel; 1815) дополнил прин­цип Гюйгенса, введя представление о когерентности элем. волн и интерфе­ренции волн, что позволило рассмот­реть на основе Г.— Ф. п. многие дифракц. явления (см. Дифракция волн, Дифракция света),

Согласно Г.— Ф. п., волн. возму­щение в нек-рой точке Р (рис. 2) можно рассматривать как результат ин­терференции элем. вторичных волн, излучаемых каждым элементом не­которой волн. поверхности. На рис. такой поверхностью явл. сферич. по­верхность АОВ волны, излучаемой точечным источником S. Если рас­сматривается распространение волн, ограниченное к.-л. препятствием (напр., отверстие в непрозрачном эк­ране, как на рисунке), то целесооб­разно выбрать волн. поверхность так, чтобы она касалась краёв пре­пятствия.

• Ландсберг Г. С., Оптика, 5 изд., М., 1976 (Общий курс физики).