2. Молекулярно-кинетическая теория идеальных газов
| Вид материала | Документы |
- Молекулярно-кинетическая теория газов, 97.72kb.
- Занятие №16 Основные положения мкт. Масса и размеры молекул. Мкт- молекулярно- кинетическая, 138.45kb.
- Контрольная работа №5 10 класс По теме: «Молекулярно-кинетическая теория. Свойства, 99.75kb.
- Молекулярно-кинетическая теория, 37.31kb.
- Молекулярная физика и основы термодинамики электронный учебник по физике кгту-кхти., 493.33kb.
- Молекулярная физика и термодинамика. Лекция №1 Молекулярно-кинетическая теория Основные, 10053.18kb.
- Программа учебной дисциплины «Кинетическая теория неравновесных смесей газов» специальность, 118.5kb.
- Контрольная работа "Молекулярно-кинетическая теория идеального газа. Газовые законы., 9.92kb.
- Вопросы к Госэкзамену по курсу общей физики из раздела, 17.7kb.
- Молекулярно-кинетическая теория. Термодинамика. Задания с выбором ответа, 110.39kb.
2. Молекулярно-кинетическая теория идеальных газов
2.1. Основные определения
Объектом исследования в молекулярно-кинетической теории является газ.
Считается, что молекулы газа, совершая беспорядочные движения, не связаны силами взаимодействия и поэтому они движутся свободно, стремясь, в результате соударений, заполнить весь предоставленный им объем: газ принимает объем того сосуда, который газ занимает.
Идеальный газ:
собственный объем его молекул пренебрежимо мал по сравнению с объемом сосуда;
между молекулами газа отсутствуют силы взаимодействия;
столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Термодинамическая система - совокупность макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой).
Состояние системы - совокупность физических величин (термодинамических параметров, параметров состояния), которые характеризуют свойства термодинамической системы: температура, давление, удельный объем.
Температура - физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.
В системе СИ разрешено использование термодинамической Т и практической t шкалы температур: T = 273.15 + t.
Давление - физическая величина, определяемая нормальной силой F, действующей со стороны газа (жидкости) на единичную площадку, помещенную внутрь газа (жидкости)
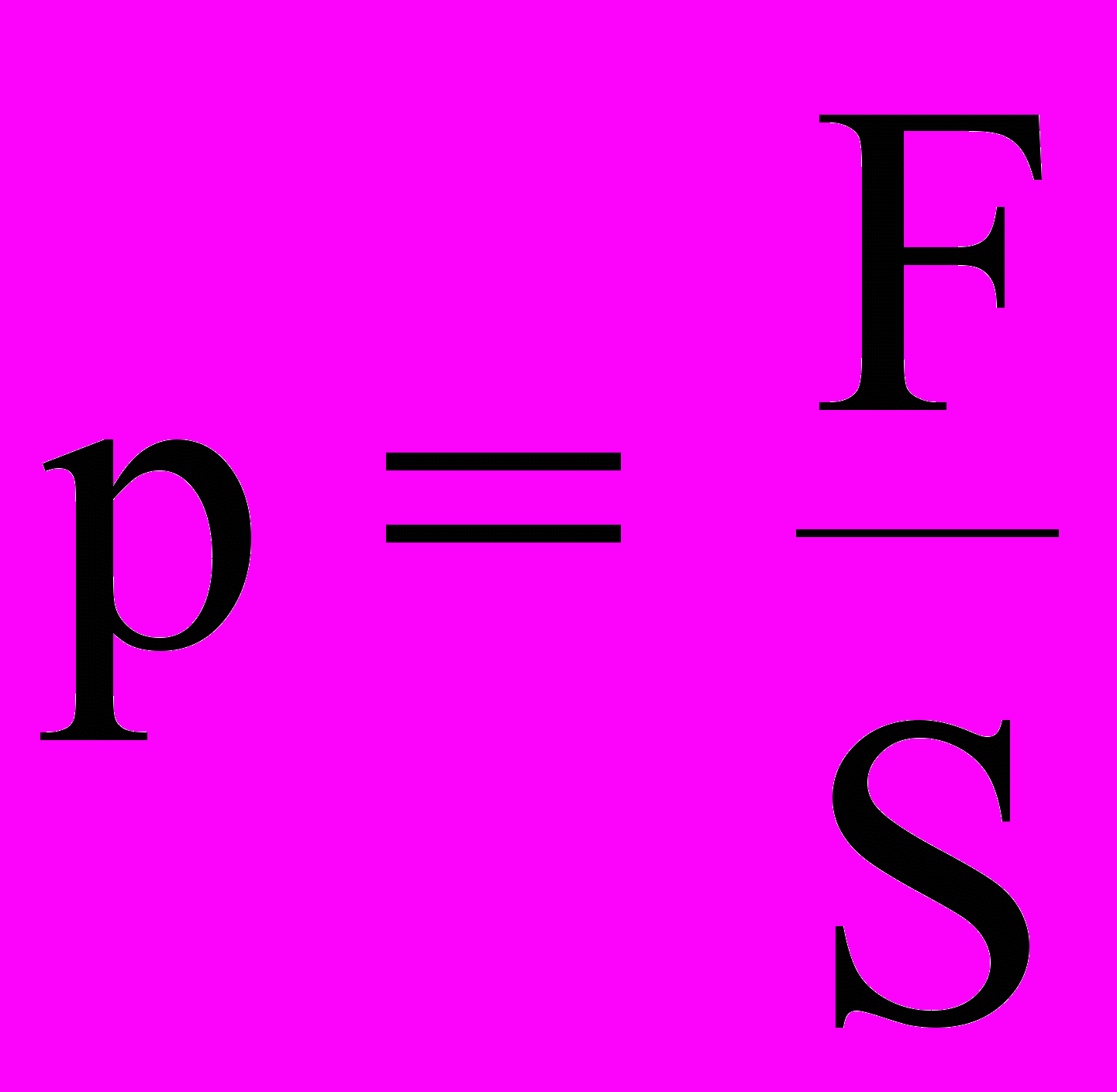, S - размер площадки. Единица давления - паскаль [Па]: 1 Па = 1
.Удельный объем - это объем единицы массы
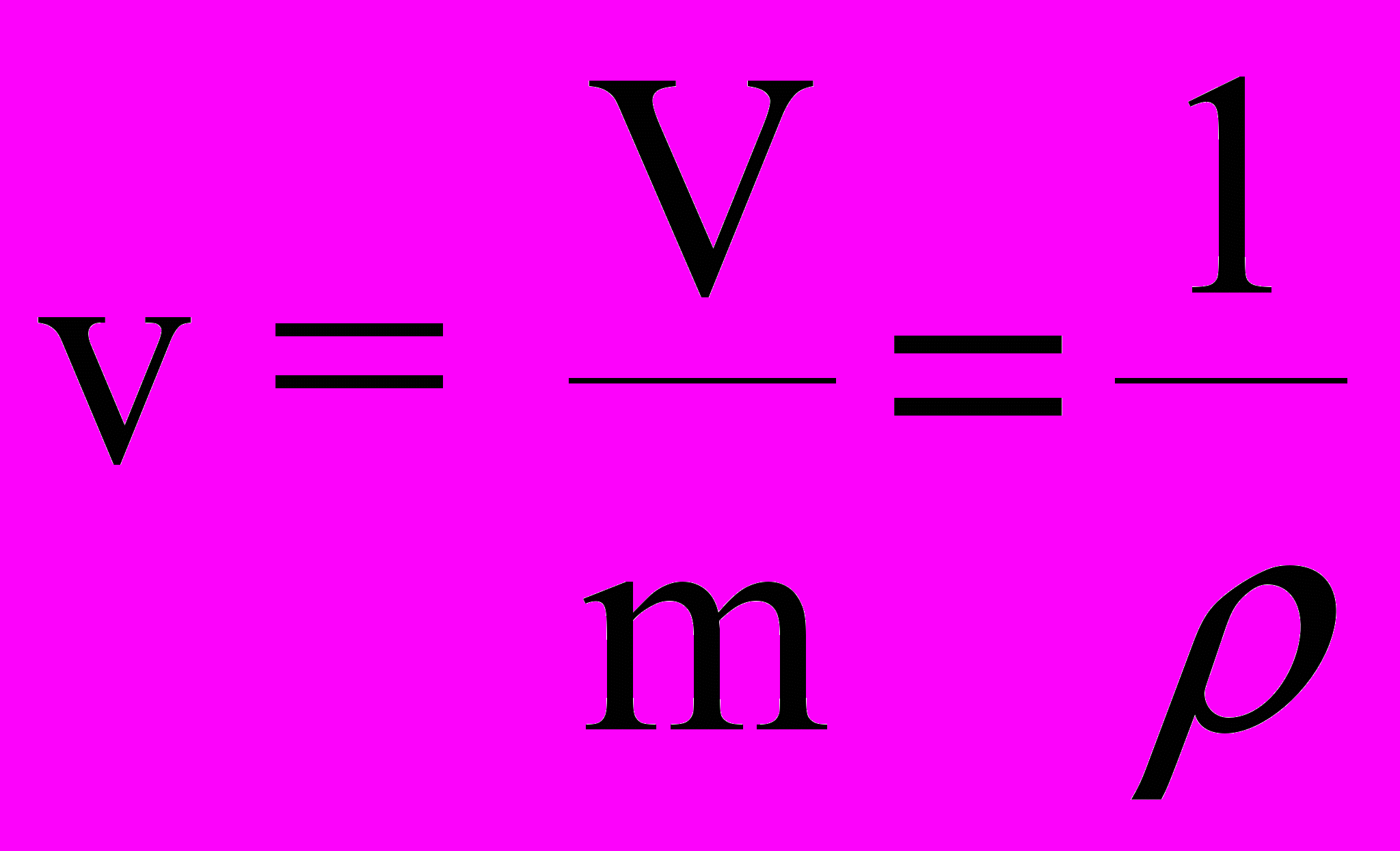
где V - объем массы m, - плотность однородного тела.
Термодинамический процесс - любое изменение в термодинамической системе, приводящее к изменению хотя бы одного из ее термодинамических параметров.
Термодинамическое равновесие - такое состояние макроскопической системы, когда ее термодинамические параметры не изменяются с течением времени.
Равновесные процессы - процессы, которые протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало.
Изопроцессы - это равновесные процессы, при которых один из основных параметров состояния сохраняется постоянным.
Изобарный процесс - процесс, протекающий при постоянном давлении (в координатах V,t он изображается изобарой).
Изохорный процесс - процесс, протекающий при постоянном объеме (в координатах p,t он изображается изохорой).
Изотермический процесс - процесс, протекающий при постоянной температуре (в координатах p,V он изображается изотермой).
Адиабатический процесс - это процесс, при котором отсутствует теплообмен между системой и окружающей средой (в координатах p,V он изображается адиабатой).
Постоянная (число) Авогадро - число молекул в одном моле NA=6.022.1023.
Нормальные условия: p = 101300 Па, Т = 273.16 К.
2.2. Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева)
Функциональная связь между давлением, объемом и температурой называется уравнением состояния.
Для идеального газа справедливо уравнение Клапейрона-Менделеева для одного моля газа
pVm = RT, (2.1a)
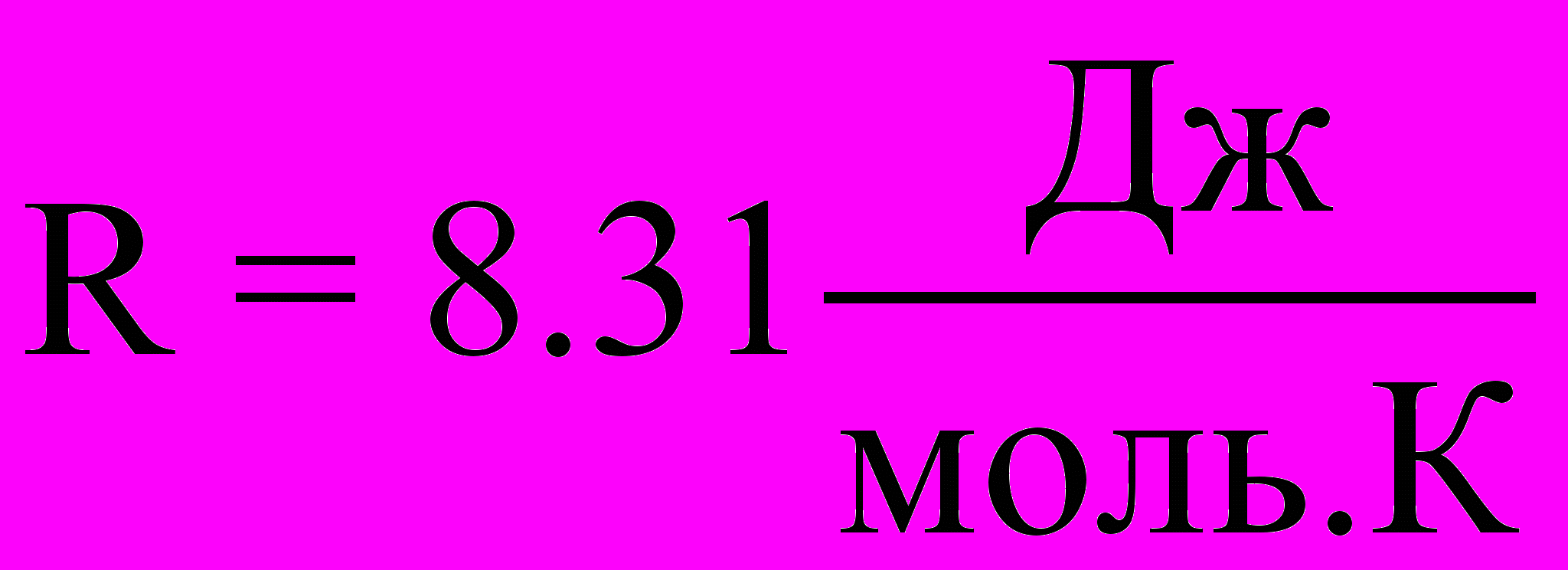- газовая постоянная и уравнение Клапейрона-Менделеева для произвольной массы газа
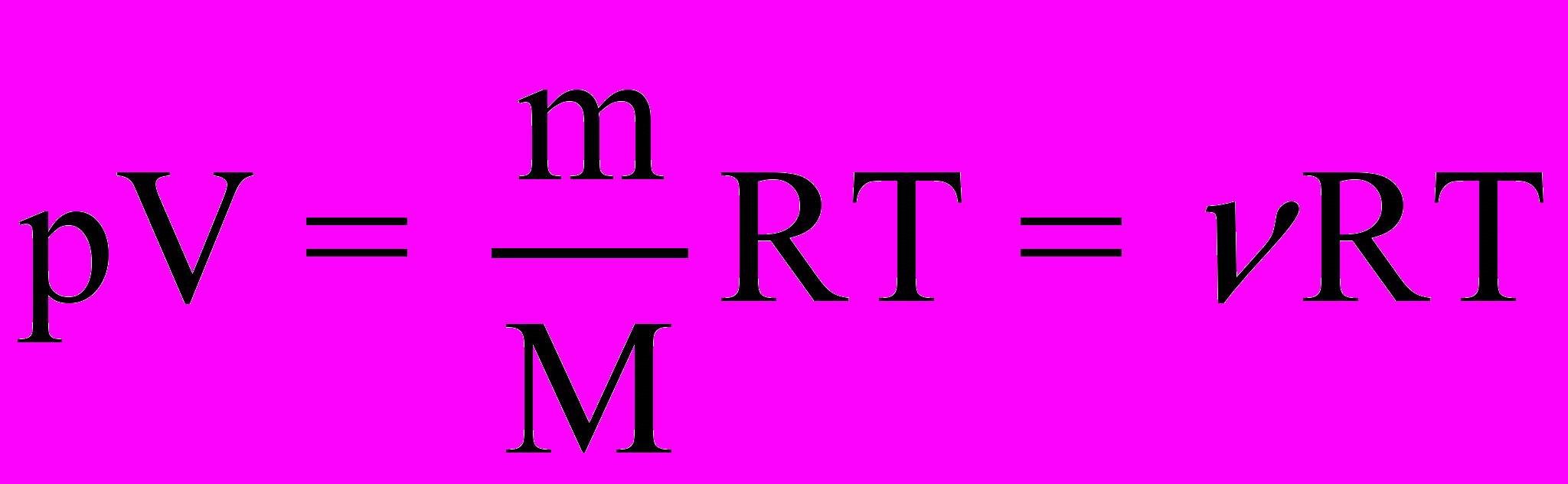(2.1b)М - масса одного моля (молярная масса),
- количество вещества.Если ввести постоянную Больцмана
,то уравнение Клапейрона-Менделеева имеет вид
p = nkT, (2.1c)
n = NA/Vm - число молекул в единице объема.
2.3. Основное уравнение молекулярно-кинетической теории идеальных газов выводится в предположении, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие:
(2.2)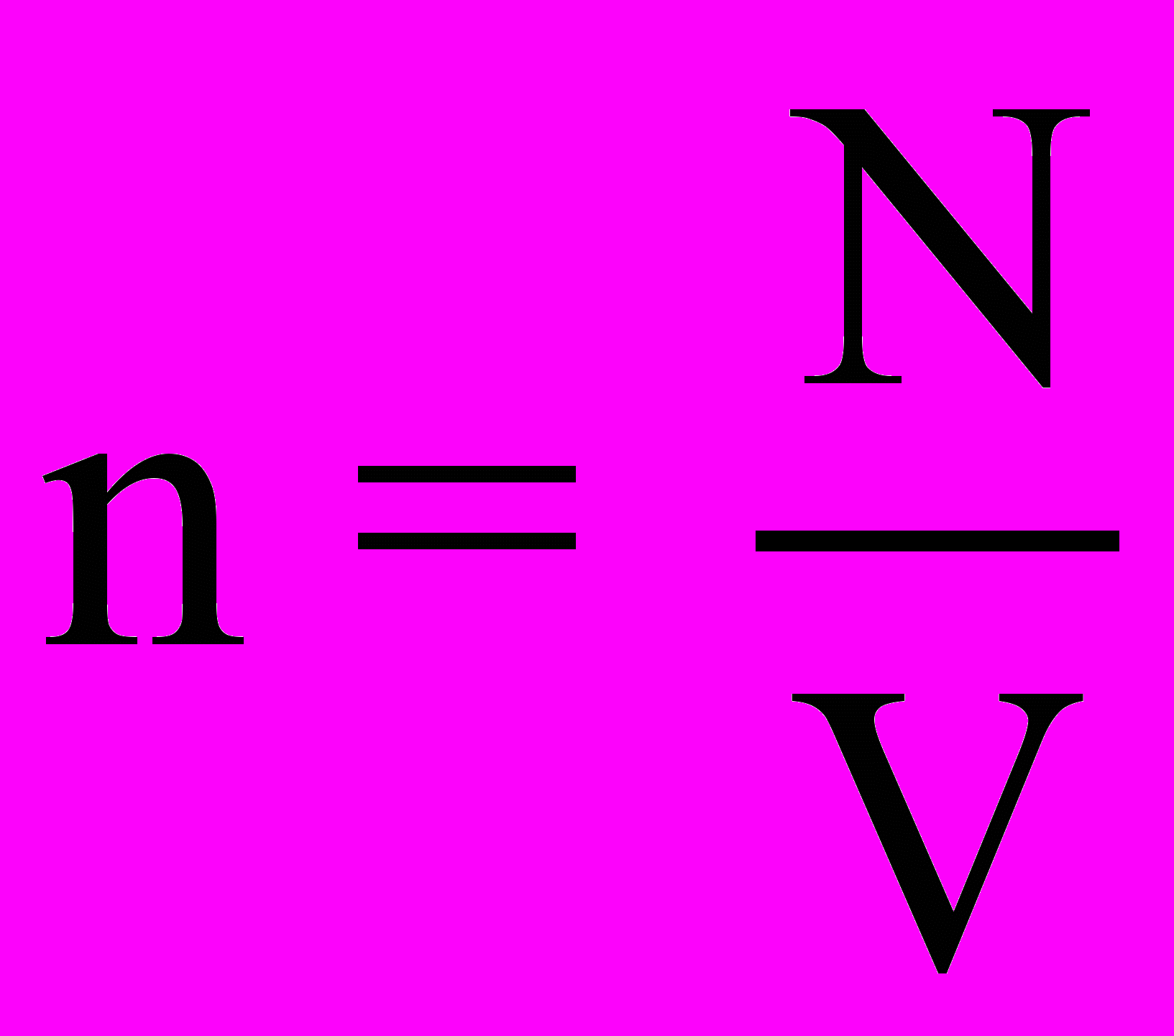
- концентрация молекул газа, N - число молекул газа,
V - объем газа,
- среднеквадратичная скорость молекул, vi - скорость i-молекулы,
m - масса одной молекулы.
Суммарная кинетическая энергия поступательного движения всех молекул газа
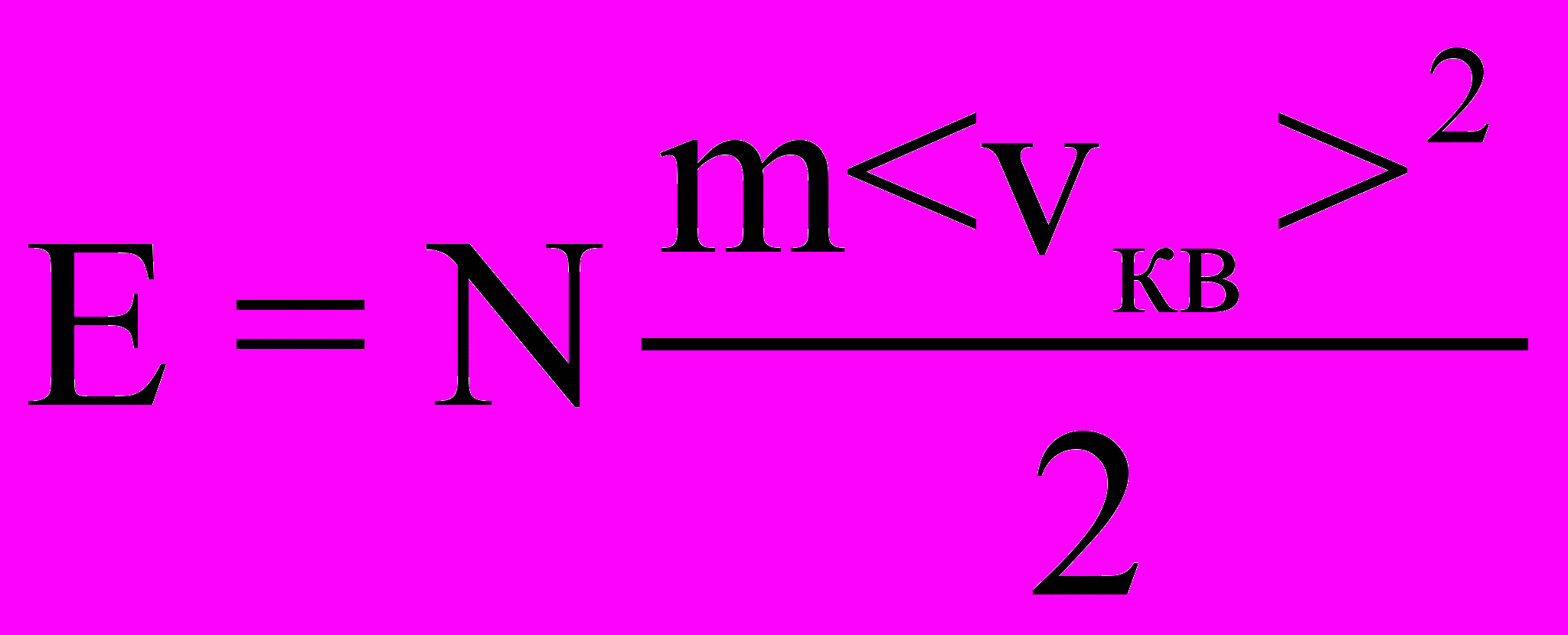
и, следовательно, уравнение (2.2) можно записать
. Если сравнить уравнение (2.2) с уравнением Клапейрона-Менделеева (2.1), то можно получить выражения для среднеквадратичной скорости молекул
(2.3)и для средней кинетической энергии поступательного движения одной молекулы идеального газа
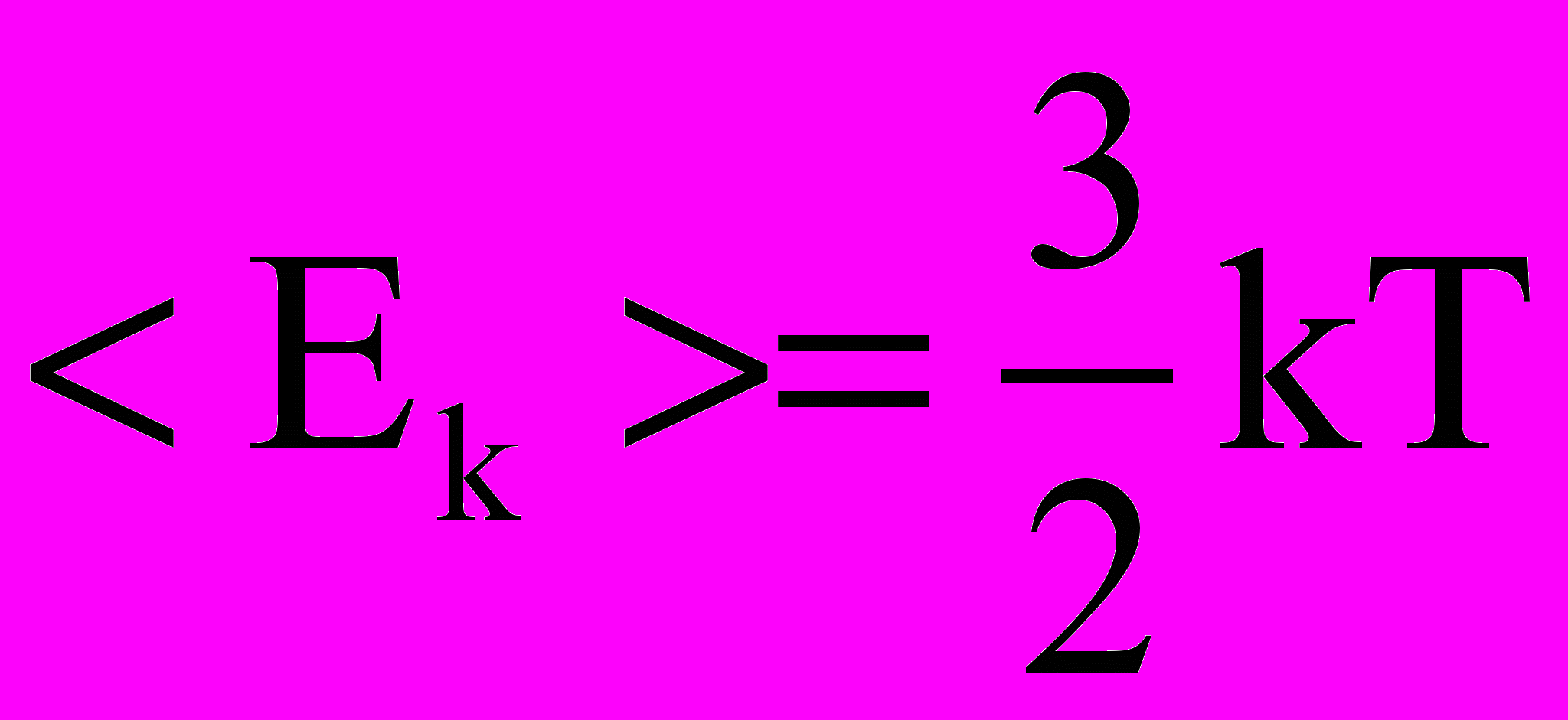(2.4)Таким образом, термодинамическая температура Т является мерой средней кинетической энергии поступательного движения молекул идеального газа и формула (2.4) раскрывает молекулярно-кинетическое толкование температуры.
2.4. Распределение Максвелла
В газе, находящемся в состоянии равновесия, устанавливается стационарное, не меняющееся со временем распределение молекул по скоростям.
Пусть имеетcя N молекул, причем dN(v) - число молекул, имеющих скорость в интервале от v до dv.
Как показал Максвелл, для идеального газа справедлив закон распределения молекул идеального газа по скоростям (распределение Максвелла)
dN(v)= Nf(v), (2.5)
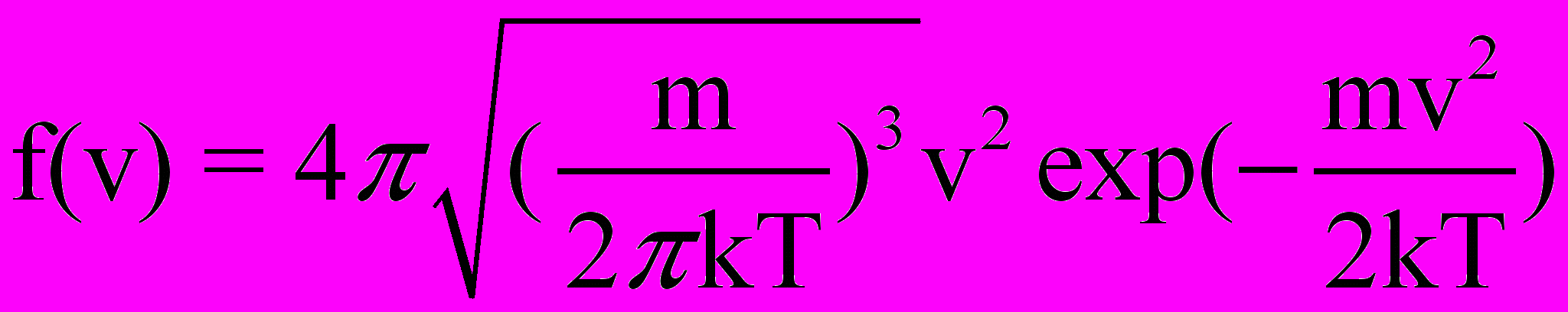
- функция распределения молекул по скоростям (рис.4).
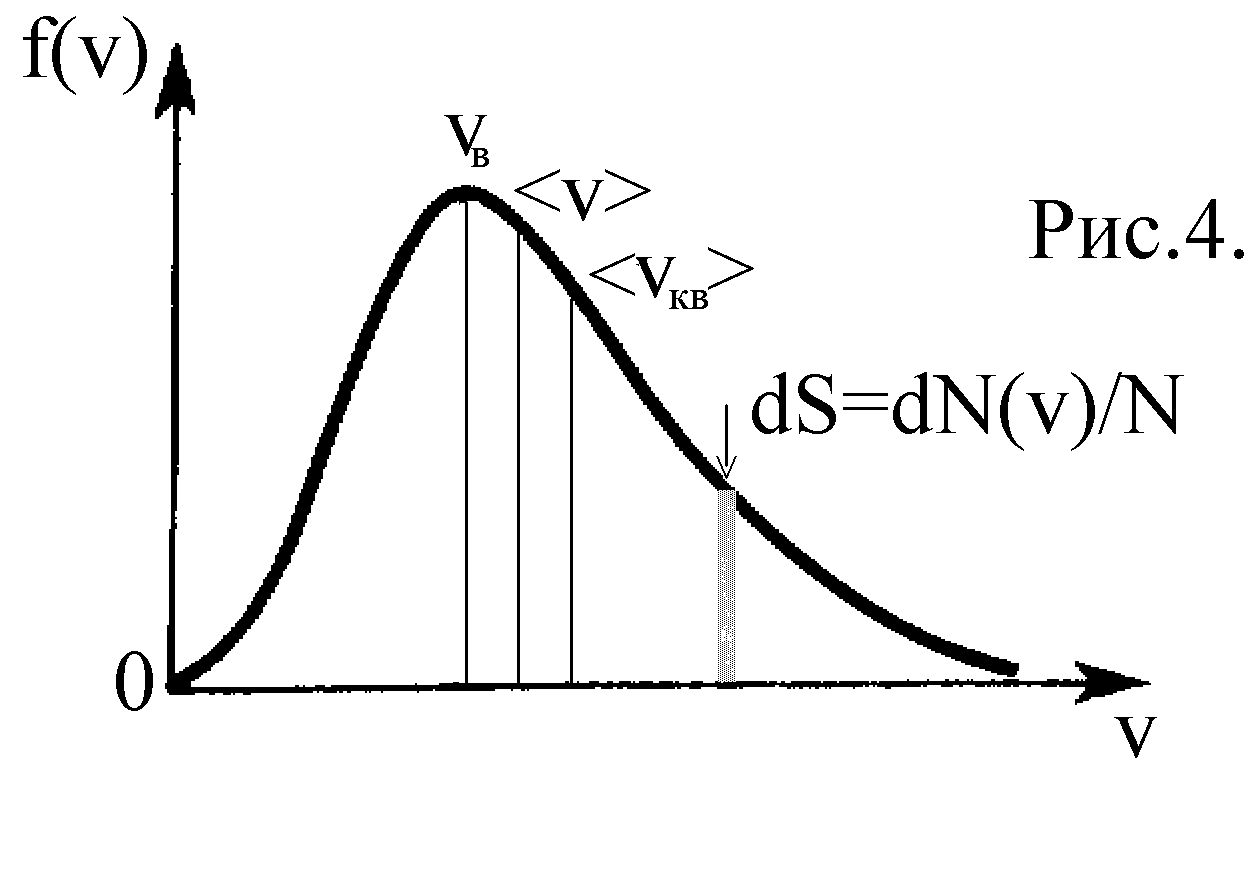
Площадь под кривой f(v) равна единице, т.е. функция f(v) нормирована на единицу
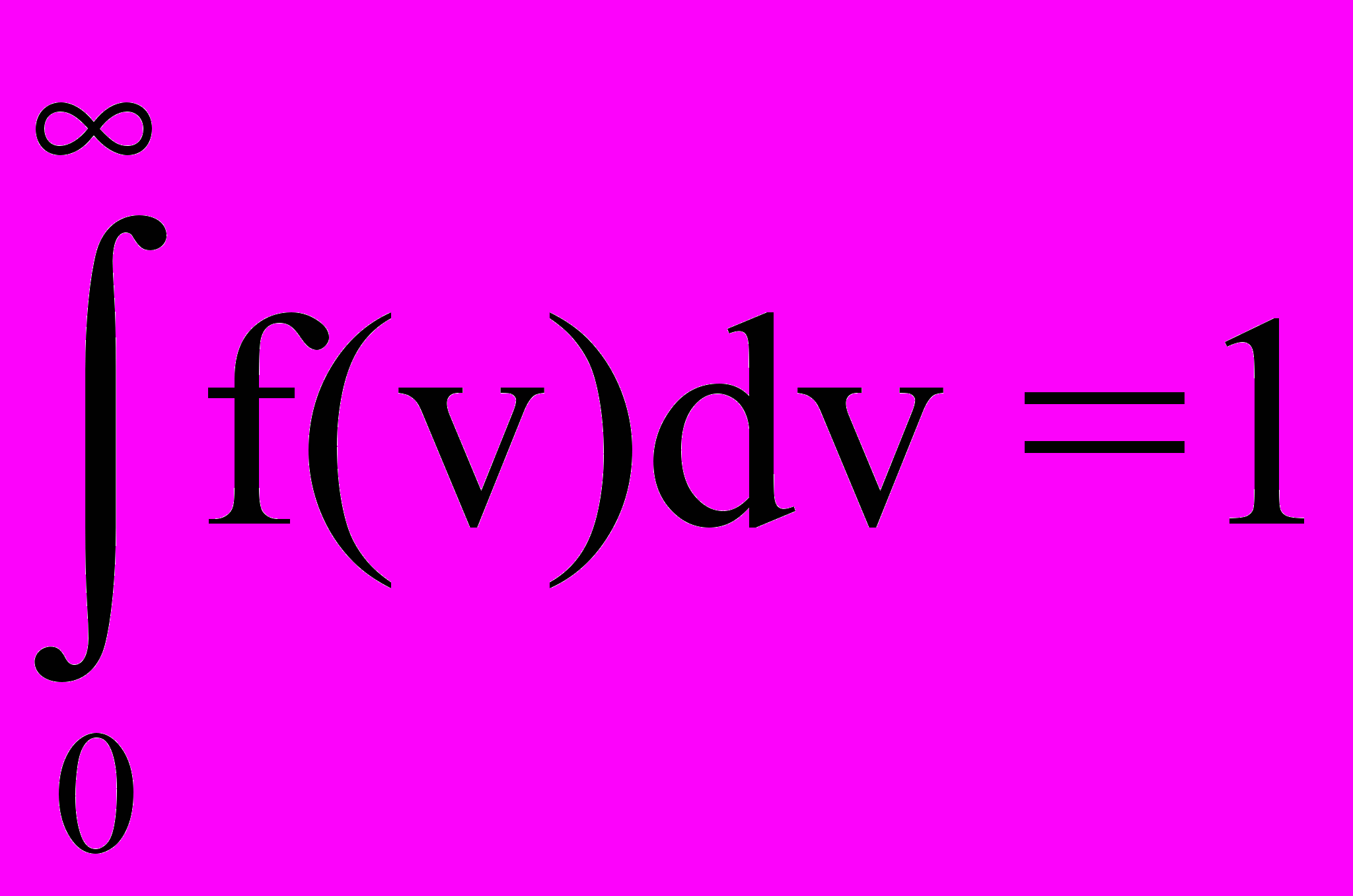.Относительное число молекул, скорости которых лежат в интервале от v до v+dv, определяется
(заштрихована на рис.4). Скорость, при которой функция распределения f(v) максимальна, называется наиболее вероятной скоростью
(эта скорость находится путем дифференцирования функции f(v) по аргументу v и приравнивания результата нулю).
Повышение температуры смещает распределение молекул по скоростям, увеличивая vв, однако площадь под f(v) неизменна (рис.5).
2.6. Распределение Максвелла-Больцмана
Из распределения (2.5) можно найти распределение молекул по кинетическим энергиям (распределение Максвелла-Больцмана) (для этого следует перейти от переменной v к переменной
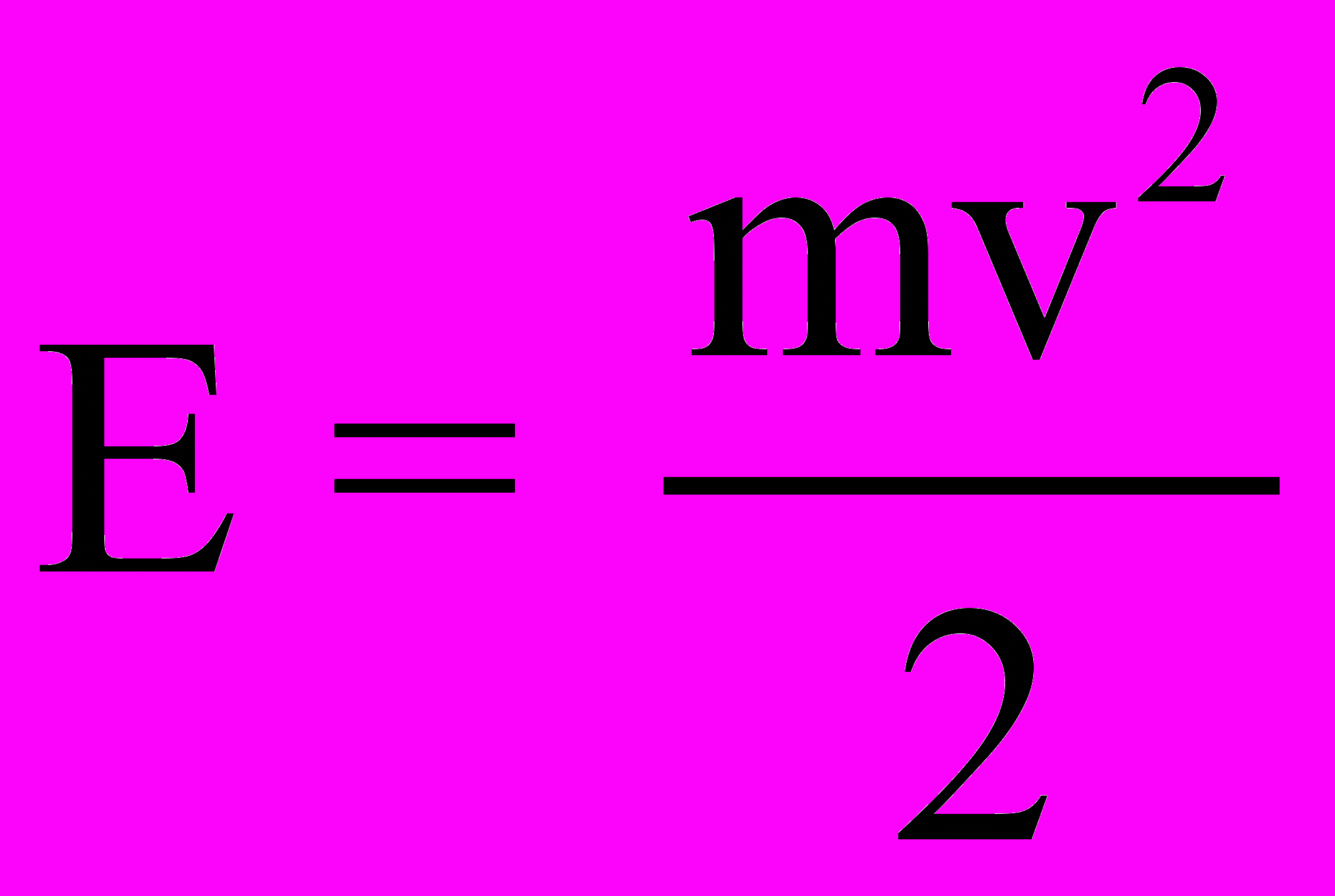): число молекул, имеющих кинетическую энергию, заключенную в интервале энергий от E до E+dE, равноdN(E) = Nf(E), (2.6)
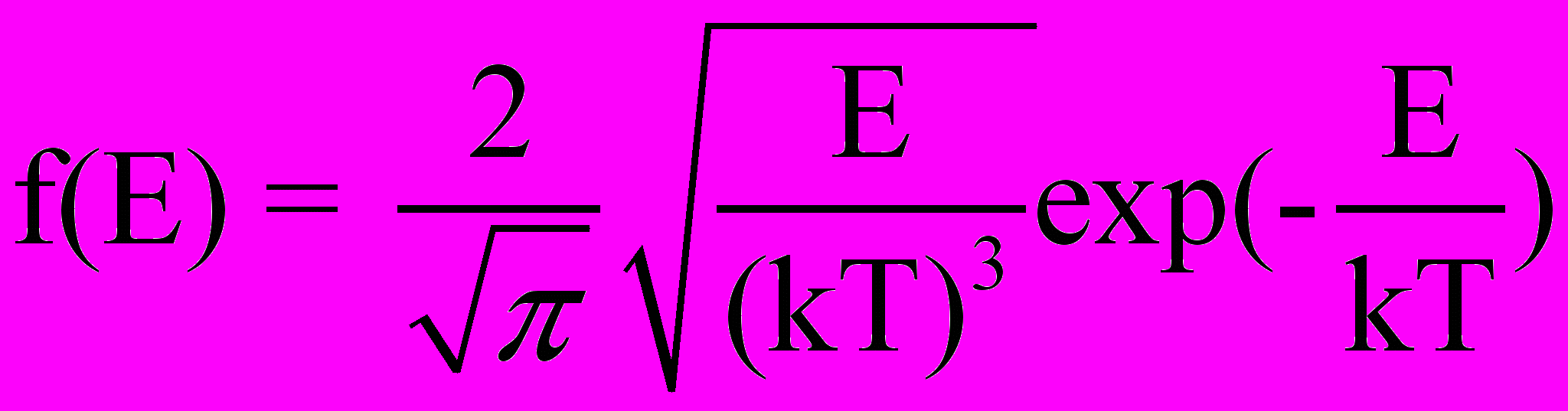
- функция распределения молекул по кинетическим энергиям.
Тогда средняя кинетическая энергия
т.е. получили результат, совпадающий с (2.4).
Рис.6. Сплошная линия Т1, пунктирная линия Т2, T2>T1