Агрегатное состояние в-ва, в к-ром его ч-цы не связаны или весьма слабо связаны силами вз-ствия и дви­жутся свободно, заполняя весь предо­ставленный им объём

• 2. Молекулярно-кинетическая теория идеальных газов, 52.42kb.
• Магия и технология – за и против (или наоборот – вместе или порознь) Гилдор Карнесир, 243.69kb.
• Тема: Инновации и инновационные процессы, 158.08kb.
• Т. И. Розбицкая Музыка в жизни и творчестве И. С. Тургенева Все виды искусства так, 46.59kb.
• Ii этап Команда «исследователи» моу «сош №2», 94.86kb.
• 1 Использование ресурсов минерально-сырьевой базы края и охрана недр, 291.61kb.
• Позиционирования (gps), 196.2kb.
• Конспект тема: Бизнес план и его роль в современном предпринимательстве, 598.08kb.
• Задания для второго (районного, городского) этапа Всероссийской олимпиады школьников, 68.78kb.
• Курсовые работы на III и IV курсах обязательно должны быть связаны, 86.91kb.

0=cp/el, и сильным, если Н>>Н₀. При комнатной темп-ре для металлов и хорошо проводящих полупроводни­ков H₀10⁵—10⁶ Э, для плохо проводя­щих полупроводников H₀10⁸—10⁹ Э. С понижением темп-ры l увеличивается и потому уменьшается Н₀. Это позво­ляет, используя обычные магн. поля 10⁴ Э, осуществлять условие H>>H₀.

При низких темп-pax наблюдаются квант. осцилляции сопротивления и постоянной Холла при изменении магн. поля (см. Шубникова — де Хааза эффект).

• Займан Дж., Электроны и фононы, пер. с англ., М., 1962; Вайcс Г., Физика гальваномагнитных полупроводниковых при­боров и их применение, пер. с нем., М., 1974; Ангрист Ст., Гальваномагнитные и тер­момагнитные явления, в кн.: Физика твердо­го тела. Электронные свойства твердых тел, пер. с англ., М., 1972 (Над чем думают фи­зики, в. 8); В о н с о в с к и й С. В., Маг­нетизм, М., 1971.

ГАЛЬВАНОМЕТР, электроизмери­тельный прибор высокой чувствитель­ности для измерения малых токов, на­пряжений и кол-ва электричества (см. Баллистический гальванометр). Ши­роко применяется в кач-ве нулевого индикатора для определения отсутст­вия тока в электрич. цепи или нулевой разности потенциалов между к.-л. двумя точками цепи. Наибольшее рас­пространение получил Г. пост. тока с магнитоэлектрическим измеритель­ным механизмом. Для повышения его чувствительности используют оптиче­ские отсчётные устройства, располагая выносную шкалу на значит. расстоянии от подвижной части механизма, либо применяют спец. оптич. систему с многократным отражением луча света. Чувствительность Г. и хар-р движения его подвижной части зависят от сопро­тивления внеш. электрич. цепи, на к-рую замкнут Г.

На практике Г. характеризуются ве­личиной, обратной чувствительности, т. н. постоянной Г. (b). В документа­ции указывают значение b при внеш. сопротивлении, равном критическому, при к-ром движение подвижной части переходит от колебательного к апериодич. Значения b у совр. Г. пост. тока достигают: потоку 10^-12 А•м/мм, по напряжению 3•10^-8 В•м/мм. В це­пях переменного тока низкой часто­ты (от 30 до 100 Гц) используют вибрац. Г. (см. Вибрационный электроиз­мерительный механизм) с постоянными по току — до 10^-8А/мм, а по напря­жению — до 2•10^-5 В/мм.

Техн. требования к Г. стандартизо­ваны в ГОСТе 22261—76 и ГОСТе 7324—80.

• Основы электроизмерительной техники, М., 1972; М и н ц М. Б., Магнитоэлектри­ческие гальванометры, М.— Л., 1963.

В. П. Кузнецов.

ГАЛЬТОНА СВИСТОК, газоструйный излучатель звук. и ультразвук. волн, работающий при малых скоростях ис­течения газа. Предложен англ. учёным Ф. Гальтоном (F. Galton; 1883). Г. с. представляет собой сопло 1 с узкой коль­цевой щелью 2 (рис.), перед к-рой располо­жен полый цилиндрич. резонатор 3 с острыми клиновидны­ми краями, 4 — по­движное дно резона­тора. Газ, выходящий из щели под небольшим избыточным давлением (обычно не больше 0,1 атм), попадает на острый край резонатора, возбуждая в нём периодич. вихри.



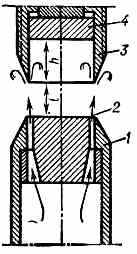
Схема свистка Гальтона.


Частота f клинового тона определяется скоростью истече­ния газа v и расстоянием l между соп­лом и остриём клина: f=0,466 iv/l, где i=1, 2, 3... Одна из гармонич. со­ставляющих (обычно первая) усили­вается резонатором и излучается в ок­ружающее пр-во в виде акустич. волн. Частота звука, излучаемого Г. с., за­висит от глубины h резонатора и поло­жения его по отношению к соплу (па­раметр l). Г. с. имеет сравнительно вы­сокий кпд (15—20%), но малую мощ­ность. Для увеличения излучаемой мощности звука применяются устрой­ства, состоящие из неск. Г. с., синхро­низация к-рых осуществляется с по­мощью полуволновых трубок, соеди­няющих полости резонаторов.

Ю. Я. Борисов.

ГАМИЛЬТОНА УРАВНЕНИЯ, то же, что канонические уравнения меха­ники.

ГАМИЛЬТОНА ФУНКЦИЯ [по име­ни ирл. математика У. Р. Гамиль­тона (W. R. Hamilton)], характеристич. функция механической систе­мы, выраженная через канонические переменные: обобщённые координаты q_i и обобщённые импульсы р_i. Для системы со связями, явно не завися­щими от времени t, движущейся в ста­ционарном потенциальном силовом по­ле, Г. ф. H(q_i, р_i)=T+П, где П — потенц. энергия, а Т — кинетич. энер­гия системы, в выражении к-рой все обобщённые скорости q_i заменены на Pi с помощью равенства р_i=дТ/дq_i. Т. о., в этом случае Г. ф. равна полной механич. энергии системы, выражен­ной через q_i и p_i. В общем случае Г. ф. H(p_i, q_i, t) может быть определена через др. характеристич. ф-цию — Лагранжа функцию L (q_i, p_i, t) равен­ством:



в к-ром все q_i должны быть также вы­ражены через p_i.

Г. ф., как и ф-ция Лагранжа, пол­ностью характеризует ту систему, для к-рой она определена, т. к., зная H(p_i, q_i, t), можно составить дифф. ур-ния движения системы (см. Кано­нические уравнения механики).

Г. ф. обобщается и на системы с бес­конечным числом степеней свободы — классические физические поля. В этом случае роль обобщён­ных координат и импульсов играют значения ф-ции поля в каждой точке пр-ва и их производные по времени. Г. ф. системы взаимодействующих по­лей равна сумме Г. ф. свободных полей и энергии их вз-ствия. (Иногда в тео­рии классич. полей Г. ф. наз. гамильтонианом, как и в теории квант. полей.)

ГАМИЛЬТОНИАН, в квантовой те­ории — оператор, соответствующий Гамильтона функции в классич. тео­рии.

В квантовой механике Г.— опера­тор (Н), определяющий изменение во времени состояния квант. системы (её волн. функции), т. е. вид Шредин­гера уравнения. Одновременно Г. явл. оператором полной энергии системы (если потенциал не зависит от време­ни). Формально он может быть полу­чен заменой обобщённых координат (q_i) и импульсов (p_i) в ф-ции Гамиль­тона классич. механики на соответст­вующие операторы (q_i, p_i), подчиняю­щиеся перестановочным соотношениям.

В классич. теории поля роль обоб­щённых координат играют ф-ции поля в каждой точке пространства-време­ни; в квантовой теории поля они ста­новятся операторами. Для системы взаимодействующих полей Г. представ-

107


ляет собой сумму операторов энергии свободных полей и энергии их вз-ствия. Как и лагранжиан, Г. определяет ур-ния движения поля, однако гамильтонов подход явл. менее общим, чем лангранжев, и, кроме того, Г. не даёт релятивистски-инвариантного описания системы (энергия в разных инерц. системах отсчёта различна).

А. В. Ефремов,

ГАММА (), 1) наименование стоты­сячной доли эрстеда, 1=10^-5Э= 7,95775•10^-4 А/м. 2) Редко применя­емая дольная ед. массы, 1=10^-9кг=10^-6 г.

ГАММА-ИЗЛУЧЕНИЕ (-излучение), коротковолновое эл.-магн. излучение. Г.-и. обладает чрезвычайно малой длиной волны (10^-8 см) и вследствие этого — ярко выраженными корпуску­лярными св-вами, т. е. является пото­ком ч-ц — гамма-квантов (фотонов) с энергией ξ_=h ( — частота из­лучения) и импульсом p=h/c.

Испускание -квантов сопровождает радиоакт. распад (см. Радиоактив­ность) в тех случаях, когда образую­щиеся ядра находятся в возбуждённых состояниях. При переходе ядра с верх­него энергетич. уровня на нижний излучается -квант с энергией, равной разности энергии уровней, между к-рыми происходит переход. Время жизни ядер в возбуждённых состояниях опре­деляется св-вами (спин, чётность, энергия) данного состояния и нижеле­жащих уровней, на к-рые могут про­исходить переходы с испусканием -квантов. Время жизни -активных ядер резко возрастает с уменьшением их энергии и с увеличением разности спинов исходного и конечного состоя­ний ядра. Вследствие этого наряду с осн. состоянием ядра может относи­тельно долго (иногда годы) существо­вать его метастабильное возбуждённое (т. н. изомерное) состояние (см. Изоме­рия атомных ядер). При радиоакт. распаде ядер обычно наблюдаются -кванты с энергией ξ_ от 10 кэВ до 5 МэВ. Гамма-кванты больших энер­гий возникают при распадах элем. ч-ц. Так, при распаде покоящегося ней­трального пи-мезона возникает Г.-и. с энергией ~70 МэВ.

Г.-и., появляющиеся при прохожде­нии быстрых эл-нов через в-во, обус­ловлено торможением последних в кулоновском поле ядер. Тормозное Г.-и. характеризуется сплошным спектром, верх. граница к-рого совпадает с энер­гией заряж. ч-цы. На ускорителях заряж. ч-ц получают тормозное Г.-и. с макс. энергией до неск. десятков ГэВ (см. Тормозное излучение).

Г.-и. обладает большой проникаю­щей способностью. Осн. процессы, про­исходящие при вз-ствии Г.-и. с в-вом: фотоэффект, Комптопа эффект и рождение пар электрон—позитрон. При фотоэффекте -квант поглощается од­ним из ат. эл-нов, причём энергия -кванта преобразуется (за вычетом энергии связи эл-на в атоме) в кинетич. энергию эл-на, вылетающего за преде­лы атома. Вероятность фотоэффекта с K-оболочки прямо пропорц. Z⁵ (Z — ат. номер) и быстро убывает с увели­чением энергии фотона (см. рис.). Т. о., фотоэффект преобладает в области ма­лых энергий -квантов (ξ_100 кэВ) и у тяжёлых элементов (Pb, U).



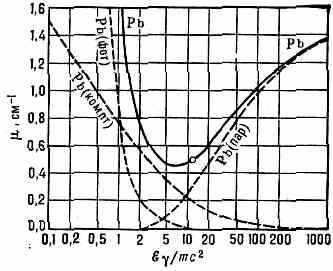
Зависимость коэфф. поглощения  -излучения в свинце от энергии -квантов.


В случае Комптона эффекта проис­ходит рассеяние -кванта на одном из ат. эл-нов. При этом уменьшается энер­гия -кванта (увеличивается длина волны) и изменяется направление его распространения. Вероятность комптоновского рассеяния пропорц. числу эл-нов в атоме, т. е. Z. Она убывает с ростом энергии -кванта ξ_ , но значительно медленнее, чем при фото­эффекте. Поэтому для Pb, несмотря на большое Z (Z=82), вероятность комптоновского рассеяния сравнима с вероятностью фотоэффекта при до­статочно больших ξ_ (~0,5 МэВ).

При ξ_ >1.,02 МэВ=2 mc² (m — масса покоя эл-на) становится воз­можным процесс образования электронно-позитронных пар в электрич. полях ядер. Вероятность этого про­цесса пропорц. Z² и увеличивается с ростом ξ_. Поэтому при ξ_ ~10 МэВ осн. процессом поглощения Г.-и. в любом в-ве оказывается образование пар.

Ослабление Г.-и. в в-ве обычно ха­рактеризуют линейным коэфф. погло­щения , к-рый показывает, на какой толщине х поглотителя интенсивность I₀ падающего пучка Г.-и. ослабляется в е раз: I=I₀e^-x. Иногда вводят массо­вый коэфф. поглощения, равный отно­шению  к плотности поглотителя; в этих случаях толщину измеряют в г/см². При высоких энергиях Г.-и. (ξ_>10 МэВ) процесс прохождения Г.-и. через в-во усложняется. Вторич­ные эл-ны и позитроны обладают боль­шой энергией и потому могут в свою очередь создавать Г.-и. благодаря тор­мозному излучению и аннигиляции. Т. о., в в-ве возникает ряд чередую­щихся поколений -квантов, эл-нов и позитронов, т. е. происходит развитие каскадного ливня. Число ч-ц в таком ливне сначала возрастает с толщиной, достигая максимума, а

затем процессы поглощения начинают преобладать над процессами размно­жения ч-ц, и ливень затухает.

• Альфа-, бета- и гамма-спектроскопия, пер. с англ., в. 1, М., 1969: Экспериментальная ядерная физика, пер. с англ., т. 1, М., 1955. См. также лит. при ст. Ядро атомное, Ра­диоактивность. Е. М. Лейкин.

ГАММА-КВАНТ (), фотон большой энергии (обычно выше 100 кэВ). Г.-к. возникают, напр., при квант. перехо­дах в ат. ядрах, нек-рых превращени­ях элем. ч-ц, тормозном и синхротронном излучении эл-нов высокой энергии.

ГАММА-СПЕКТРОМЕТР, прибор для измерения энергии квантов гамма-излучения и его интенсивности (числа -кван­тов в 1 с). В большинстве Г.-с. энер­гия -квантов определяется по энер­гии заряж. ч-ц, возникающих в ре­зультате вз-ствия -излучения с в-вом. Оси. хар-ками Г.-с. явл, эффек­тивность и разрешающая способность. Эффективность оп­ределяется вероятностями образования вторичной ч-цы и её регистрации. Разрешающая способность Г.-с. ха­рактеризует возможность разделения двух -линий, близких по энергии. Мерой разрешающей способности обычно служит относит. ширина ли­нии, получаемой при измерении монохроматич. -излучения; количественно она определяется отношением ξ/ξ, где ξ — ширина линии (в энергетич. единицах) на половине её высоты, ξ — энергия вторичной ч-цы.

В магн. Г.-с. (рис. 1) эл-ны или по­зитроны возникают при поглощении



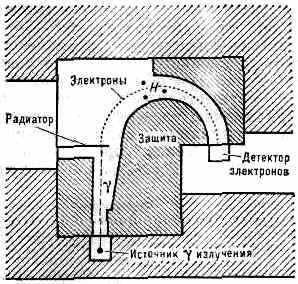
Рис. 1. Схематич. изображение магн. -спектрометра. В магн. поле H, направлен­ном перпендикулярно плоскости рисунка, вторичные эл-ны движутся по окружностям, радиусы к-рых определяются энергией эл-нов и полем H. При изменении поля де­тектор регистрирует эл-ны разных энергий. Защита из свинца заштрихована.


-квантов в т. н. радиаторе; их энер­гия измеряется так же, как и в магн. бета-спектрометрах. В радиаторе из в-ва с малым Z (Z — ат. номер) эл-ны образуются в осн. в результате Комптона эффекта, в радиаторе из в-ва с большим Z, если энергия -кваитов невелика, эл-ны возникают гл. обр. вследствие фотоэффекта. При энер­гиях h=1,02 МэВ становится воз-

108


можным образование электрон-позитронных пар. В парном Г.-с. образова­ние пар происходит в тонком радиато­ре, располож. в вакуумной камере. Измерение суммарной энергии эл-на и позитрона позволяет определить энергию -кванта.

Магн. Г.-с. обладают высокой раз­решающей способностью (обычно по­рядка 1% или долей %), однако их



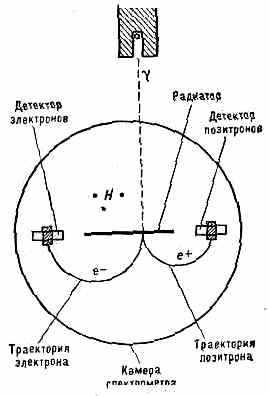
Рис. 2. Схематич. изображение парного -спектрометра. В однородном магн. поле H, направленном перпендикулярно плоскости чертежа, эл-ны (е^-) и позитроны (е⁺) дви­жутся по окружностям в разные стороны.


эффективность невелика, что приво­дит к необходимости применять ин­тенсивные -источники. Они в значит. мере вытеснены более эфф. приборами, гл. обр. сцинтилляционяыми Г.-с., к-рые также регистрируют вторичные эл-ны, возникающие при вз-ствии -квантов с кристаллом (см. Сцинтилляционный счётчик), и ПП Г.-с., осно­ванными на образовании -квантом в ПП кристалле электронно-дырочных пар (см. Полупроводниковый детек­тор).

Наивысшую точность измерения энергии -квантов обеспечивают кристалл-дифракционные спектрометры, в к-рых непо­средственно измеряется длина волны -излучения. Такой Г.-с. аналогичен приборам для наблюдения дифракции рентгеновских лучей. Гамма-излучение, проходя через кристаллы кварца или кальцита, отражается плоскостями кристалла в зависимости от длины вол­ны под тем или иным углом и регист­рируется. Недостаток таких Г.-с.— низкая эффективность.

Для измерения -спектров низких энергий (до 100 кэВ) часто применяют­ся пропорциональные счётчики. Изме­рение энергии -излучения очень боль­ших энергий осуществляется с помо­щью ливневых детекторов, к-рые измеряют суммарную энергию ч-ц электронно-позитронного ливня, вызванного -квантом высокой энер­гии. Образование ливня обычно про-

исходит в радиаторе больших разме­ров (к-рые обеспечивают полное по­глощение всех вторичных ч-ц). Вспыш­ки флюоресценции или черенковского излучения регистрируются ФЭУ (см. Черенковский счётчик).

В нек-рых случаях для измерения энергии -квантов используется фото­расщепление дейтрона. Если энергия -кванта превосходит энергию связи дейтрона (~2,23 МэВ), то может про­изойти расщепление дейтрона на про­тон и нейтрон (см. Фотоядерные реак­ции). Измеряя кинетич. энергии этих ч-ц, можно определить энергию падаю­щих -квантов.

• Альфа-, бета- и гамма-спектроскопия, пер. с англ., в. 1, М., 1969. См. также лит. при ст. Детекторы ядерных излучений.

В. П. Парфёнова, Н. Н. Делягин.

ГАММА-ЭКВИВАЛЕНТ ИСТОЧНИ­КА, условная масса точечного радио-акт. источника ²²⁶Ra (находящегося в равновесии с короткоживущими про­дуктами распада), к-рый в сочетании с платиновым фильтром толщиной 0,5 мм создаёт на нек-ром расстоянии такую же мощность экспозиц. дозы, -как данный источник на том же рас­стоянии (если бы он был также точеч­ным). Спец. ед. Г.-э. и.— килограмм-эк­вивалент радия. 1 кг-экв радия на расстоянии 1 см в воздухе создаёт мощность экспозиц. дозы 2,33 кР/с или 0,6 А/КГ.

Г. Б. Радзиевский.

ГАННА ЭФФЕКТ, генерация ВЧ коле­баний электрич. тока в полупроводнике с N-образнои вольт-амперной характе­ристикой (рис. 1). Г. э. обнаружен амер. физиком Дж. Ганном (J. Gunn;



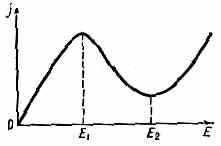
Рис. 1. N-образная вольт-амперная хар-ка: Е — электрич. поле, создаваемое приложен­ной разностью потенциалов; j — плотность тока.

1963) в кристалле GaAs с электронной проводимостью. Генерация возникает, если пост. напряжение U, приложен­ное к образцу длиной l, таково, что ср. электрич. поле Е в образце равно: Е=U/l, что соответствует падающему участку вольт-амперной хар-ки Е₁-Е₂, на к-ром дифф. сопротивление от­рицательно (рис. 1). Колебания тока имеют вид периодич. последователь­ности импульсов (рис. 2), частота их повторения обратно пропорц. напря­жённости электрич. поля Е.

Т. э. наблюдается гл. обр. в двухдолинных ПП, зона проводимо­сти к-рых состоит из одной ниж. доли­ны и неск. верх. долин (см. Зонная теория). Подвижность эл-нов в верх. долинах значительно меньше, чем в ниж. долине. В сильных электрич. полях происходит разогрев эл-нов (см. Горячие электроны), и часть эл-нов переходит из ниж. долины в верхние,

вследствие чего ср. подвижность эл-нов и, следовательно, электропроводность уменьшаются. Это приводит к умень­шению плотности тока j с ростом Е в полях Е>Е₁.

Г. э. вызван тем, что в образце пери­одически появляется, перемещается по нему и исчезает область сильного элек­трич. поля, наз. доменом Ганна. Домен возникает в результате того, что



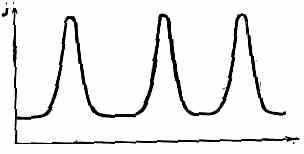
Рис. 2. Форма колебаний тока при эффекте Ганна.

однородное распределение электрич. поля при объёмном отрицат. дифф. сопротивлении неустойчиво. Действи­тельно, если в ПП случайно возникает неоднородное распределение концент­рации эл-нов в виде дипольного слоя, то между заряж. областями создаётся дополнит. поле E (рис. 3).




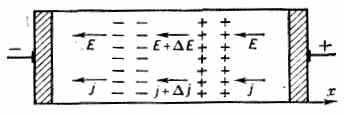
Рис. 3. Развитие электрич. домена. Эл-ны движутся слева направо, против поля.


Если об­ласть повыш. концентрации эл-нов находится ближе к катоду, то E до­бавляется к внеш. полю, так что поле внутри дипольного слоя становится больше, чем вне его. Если при этом дифф. сопротивление образца положи­тельно, т. е. ток растёт с ростом поля, то ток и внутри слоя больше, чем вне его (j>0). Поэтому, напр., из области с повыш. плотностью эл-нов они выте­кают в большем кол-ве, чем втекают, в результате чего неоднородность расса­сывается. Если же дифф. сопротивле­ние отрицательное (ток уменьшается




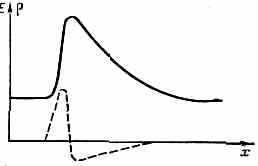
Рис. 4. Распределение электрич. поля Е (сплошная кривая) и объёмного заряда о (пунктирная кривая) в домене Ганна.


с ростом поля), то ток меньше там, где Е больше, т. е. внутри слоя, и неодно­родность не рассасывается, а нараста­ет. Растёт и падение напряжения на дипольном слое, а вне его падает (т. к. полное напряжение на образце зада­но). В результате образуется элект-

109


рич. домен (рис. 4). Вне домена Е<Е₁ (рис. 1), благодаря чему новые домены не образуются. Устойчивое состояние образца — состояние с одним доме­ном.

Т. к. домен образован эл-нами про­водимости, он движется в направлении их дрейфа со скоростью v, близкой к дрейфовой скорости носителей вне домена. Обычно домен возникает вбли­зи катода и, дойдя до анода, исчезает. По мере его исчезновения падение на­пряжения на домене уменьшается, а на остальной части образца соотв. растёт. Одновременно возрастает ток в образце, т. к. увеличивается поле вне домена. По мере приближения по­ля к e₁ ток j приближается к j_макс. Когда вне домена Е>Е₁, у катода на­чинает формироваться новый домен, ток уменьшается и процесс повторяет­ся. Частота колебаний тока f=v/l.

В GaAs с электронной проводи­мостью при комнатной темп-ре Е₁~3•10³В/см, v~10⁷ см/с и при l= 50—300мкм, f=0,3—2 ГГц. Размер домена ~10—20 мкм. Г. э. наблюдает­ся помимо GaAs и InP также в элек­тронных ПП CdTe, ZnS, InSb, InAs и др., а также в Ge с дырочной прово­димостью. Г. э. используется для соз­дания генераторов и усилителей СВЧ.

• Г а н н Дж., Эффект Ганна, [пер. с англ.], «УФН», 1966, т. 89, в. 1, с. 147; Волков А. Ф., К о г а н Ш. М., Физические явле­ния в полупроводниках с отрицательной диф­ференциальной проводимостью, там же, 1968, т. 96, в. 4, с. 633; Л е в и н ш т е й н М. Е., П о ж е л а Ю. К., Ш у р М. С., Эффект Ганна, М., 1975.