Робоча навчальна програма дисципліни для студентів спеціальності "механіка" та «математика» Затверджено вченою радою факультету
| Вид материала | Задача |
- Робоча навчальна програма дисципліни для студентів спеціальності «механіка» та «математика», 105.1kb.
- Робоча навчальна програма дисципліни за вільним вибором студентів для студентів спеціальності, 176.29kb.
- Робоча навчальна програма дисципліни за вільним вибором студентів для студентів спеціальності, 280.46kb.
- Робоча навчальна програма дисципліни за вільним вибором студентів для студентів спеціальності, 321.43kb.
- Робоча навчальна програма дисципліни за вільним вибором студентів для студентів спеціальності, 208.66kb.
- Робоча навчальна програма дисципліни для студентів спеціальності 030304 Археологія, 408.61kb.
- Робоча навчальна програма дисципліни Для студентів спеціальності 030303 "Видавнича, 307.17kb.
- Робоча навчальна програма дисципліни для студентів спеціальності 030304 Археологія, 246.31kb.
- Робоча навчальна програма дисципліни для студентів спеціальності 030300 Історія Затверджено, 188.45kb.
- Робоча навчальна програма дисципліни для студентів спеціальності 030304 Археологія, 279.76kb.
Київський національний університет імені Тараса Шевченка
Механіко-математичний факультет
Кафедра математичного аналізу
“Затверджую”
декан механіко-математичного
факультету, проф. ____________
Викладачі
кандидат фізико-математичних наук, доцент
Денисьєвський Микола Олексійович
кандидат фізико-математичних наук, доцент
Курченко Олександр Олексійович
кандидат фізико-математичних наук, доцент
Чайковський Андрій Володимирович
МАТЕМАТИЧНИЙ АНАЛІЗ
(І курс, І семестр)
Робоча навчальна програма дисципліни
для студентів спеціальності “механіка” та «математика»
Затверджено
вченою радою факультету
“_____” ____________
протокол № _________
Змістовий модуль 1
Тема 1. Елементи теорії множин та дійсні числа.
- Логічні символи. Операції над множинами. Правила де Моргана. Декартів добуток множин. – 2 год.
- Загальне поняття відображення або функції. Образ та прообраз. Типи функцій. Означення оберненої функції та суперпозиції функції. – 2 год.
- Рівнопотужні множини. Злічені множини та їх властивості. Приклад незліченої множини. – 2 год.
- Задача про вимір довжини відрізка. Означення дійсного числа. Порівняння дійсних чисел. – 2 год.
- Властивості дійсних чисел. Числова пряма і координати точок. – 2 год.
- Точна верхня і точна нижня межі числової множини. Теорема про існування точних меж. – 2 год.
- Дії над дійсними числами. Теорема про існування кореня натуральної степені із дійсного додатнього числа. – 2 год.
- Теорема про вкладені відрізки. Нерівність Коші. Нерівність Коші між середнім геометричним та середнім арифметичним. – 2 год.
Лабораторна робота 1. Контрольна робота з елементарної математики.
- 2 год.
Лабораторна робота 2. Логічні символи. Множини і дії над ними.
Правила де Моргана. – 2 год.
Лабораторна робота 3. Загальне поняття відображення. Образи і
прообрази. Сюр’єкція, ін’єкція, бієкція.
Обернене відображення. суперпозиція
відображень. – 2 год.
Лабораторна робота 4. Поняття функції. Множина визначення.
Функції парні, непарні, періодичні, монотонні.
Відповідні властивості графіків. Обернена функція. – 2 год.
Лабораторна робота 5. Графіки функцій і їх властивості. – 2 год.
Лабораторна робота 6. Графіки функцій заданих параметрично.
Полярні координати. – 2 год.
Лабораторна робота 7. Обмежені множини. Точна верхня та точна
нижня межі. – 2 год.
Лабораторна робота 8. Точні межі. Дійсні числа та дії над ними.
-2 год.
Лабораторна робота 9. Контрольна робота. Дії над множинами.
Побудова графіків функцій. Точні межі. Дійсні
числа. – 2 год.
Самостійна робота – 32 год. (опрацювання лекційного матеріалу і виконання домашніх завдань).
Контрольні запитання і завдання.
- Поняття множини. Різні способи задання множини.
- Поняття підмножини. Рівність множин.
- Об’єднання, перетин та різниця множин. Доповнення до множини.
- Закони двоїстості.
- Впорядковані пари. Добуток множин.
- Загальне означення функції. Множини визначення і множина значень функції. Рівність функцій. Звуження і продовження функцій. Графік функцій.
- Сюр’єкція, ін’єкція та бієкція.
- Суперпозиція функцій, обернена функція.
- . Злічені множини. Властивості злічених множин.
- Задача про вимір довжини відрізка. Нескінченна десяткова дріб.
- Означення дійсного невід’ємного числа. Цілі, раціональні та ірраціональні числа.
- Порівняння дійсних чисел.
- Числова пряма і координати точок.
- Найпростіші властивості дійсних чисел.
- Означення найбільшого та найменшого елемента числової множини.
- Означення обмеженої знизу та обмеженої зверху множини дійсних чисел. Означення точної нижньої межі та точної верхньої межі числової множини.
- Критерій точних меж.
- Теорема про існування точних меж.
- Означення арифметичних дій над дійсними числами.
- Теорема про існування кореня натурального степеня із дійсного числа.
- Лема про вкладені відрізки.
- Нерівність Коші.
- Середні значення. Нерівність Коші між середнім геометричним і середнім арифметичним.
Змістовий модуль 2
Тема 2. Границя послідовності дійсних чисел.
- Означення границі числової послідовності. Теорема про границі. Приклади. – 2 год.
- Властивості збіжних послідовностей. Теорема про три послідовності та арифметичні дії над збіжними послідовностями. – 2 год.
- Теорема Тьопліца про регулярне перетворення збіжних послідовностей. – 2 год.
- Теорема штольца. Приклади застосування. – 2 год.
- Теорема про існування границі монотонної послідовності. Число е. – 2 год.
- Підпослідовності. Часткові границі. Теореми про існування монотонної підпослідовності і Больцано-Вейєрштраса. – 2 год.
- Верхня і границі послідовності та теорема про їх характеризацію. Фундаментальні послідовності та критерій Коші. – 2 год.
Лабораторна робота 10. Границя послідовності дійсних чисел.
Обчислення границі за означенням. – 2 год.
Лабораторна робота 11. Властивості збіжних послідовностей. Теорема
про границю суми, добутку і частки. – 2 год.
Лабораторна робота 12. Границя послідовності. Теореми Тьопліца і
Штольца. – 2 год.
Лабораторна робота 13. Границя монотонної послідовності. – 2 год.
Лабораторна робота 14. Підпослідовності. Часткові границі та їх
характеризація. Верхня та нижня границі
послідовності. – 2 год.
Лабораторна робота 15. Фундаментальні послідовності і критерій
Коші.
Самостійна робота – 32 год. (опрацювання лекційного матеріалу і виконання домашніх завдань).
Контрольні запитання і завдання.
- Обмежені послідовності дійсних чисел.
- Означення границі послідовності дійсних чисел. Теорема про упченк границі.
- Приклади знаходження границь послідовностей
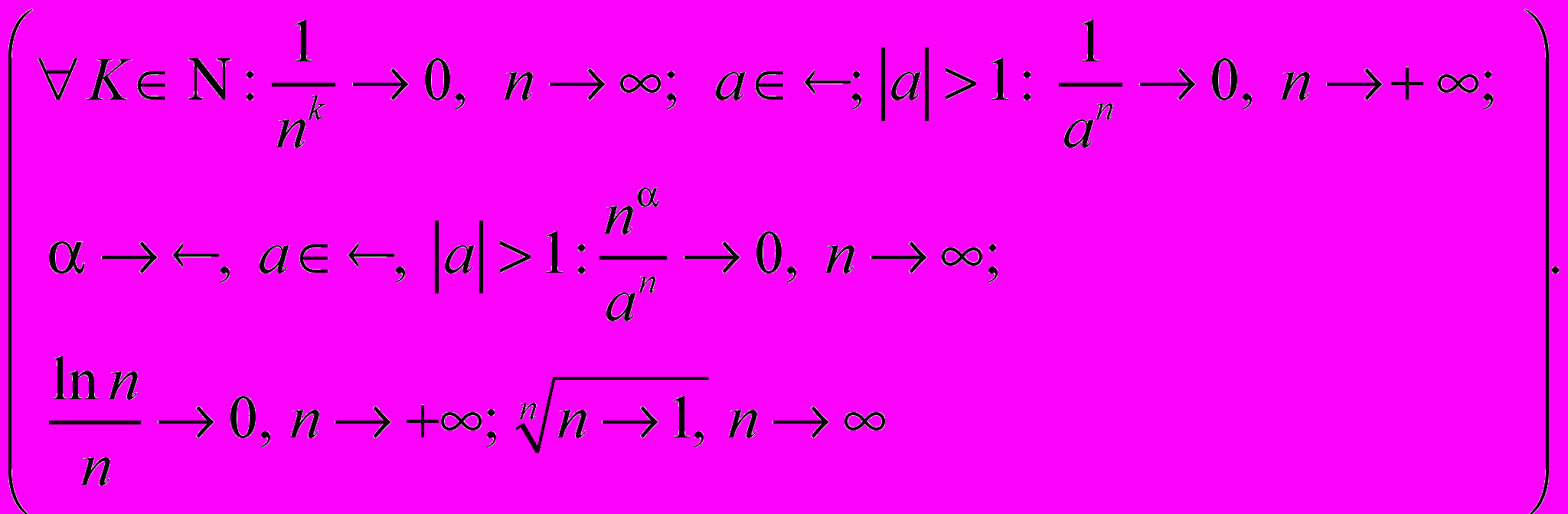
- Найпростіші властивості збіжних послідовностей.
- Теорема про три послідовності.
- Теорема про арифметичні операції над збіжними послідовностями.
- Теорема Тьопліца і теорема Штольца.
- Монотонні послідовності і теореми про існування границі монотонної послідовності.
- Число е.
- Підпослідовності і їх властивості. Часткові границі послідовності.
- Теорема про характеризацію часткової границі.
- Теорема про існування монотонної підпослідовності. Теорема Больцано-Вейєрштраса.
- Означення верхньої та нижньої границі послідовності.
- Теорема про характеризацію верхньої і нижньої границі послідовності.
- Фундаментальні послідовності та їх властивості.
- Критерій Коші збіжності числової послідовності.
- Визначення границі послідовності векторів.
Змістовий модуль 3
Тема 3. Границя функції в точці. Неперервні функції.
16. Гранична точка множини та критерій граничної точки. Означення границі
функції в точці за Коші і за Гейне. Приклади – 2 год.
17. Рівносильність означень Коші і Гейне границі функції в точці. – 2 год.
18. Односторонні границі. Теорема про існування границі монотонної функції
в точці – 2 год.
19. Відношення підпорядкованості “О”, нехтування “о” та еквівалентності і їх
властивості. Приклади. – 2 год.
20. Порядок однієї функції відносно іншої. Шкала порівнянь. Приклади. –
2 год.
21. Головна частина функції відносно шкали порівнянь. головної
частини. Асимптотичний розклад функцій відносно шкали порівнянь. –
2 год.
22. Неперервні функції. Приклади. Найпростіші властивості неперервних
функцій. – 2 год.
23. Теорема про існування і неперервність оберненої функції. Приклади
застосувань. – 2 год.
24. Чудові границі. Перша та друга теореми Вейєрштраса і теорема Коші про
обертання неперервної функції в нуль. – 2 год.
25. Застосування теореми Коші. Рівномірна неперервність функції та теорема
Кантора. – 2 год.
26. Точки розриву функції та їх класифікація. Многочлени Бернштейна та
теорема Вейєрштраса про наближення неперервної функції многочленами.
- 2 год.
Лабораторна робота 16. Границя функції в точці. Арифметичні дії над
границями. – 2 год.
Лабораторна робота 17. Границя функції в точці за Коші і за Гейне. –
2 год.
Лабораторна робота 18. Обчислення границь функцій в точці. – 2 год.
Лабораторна робота 19. Односторонні границі. Відношення “О”, “о” та
їх класифікація. – 2 год.
Лабораторна робота 20. Неперервні функції. Точки розриву та їх
класифікація. – 2 год.
Лабораторна робота 21. Властивості неперервних функцій. Рівномірна неперервність. – 2 год.
Тема 4. Похідна та її застосування.
27. Означення похідної. Приклади. Фізична та геометрична інтерпретація
похідної. Правила обчислення похідних. – 2 год.
28. Похідна складної та оберненої функції. Приклади обчислення похідних. –
2 год.
29. Основні теореми диференціального числення: теореми Ферма, Ролля,
Лагранжа і Коші. – 2 год.
30. Приклади застосування основних теорем диференціального числення. –
2 год.
31. Дослідження монотонності функції за допомогою похідних. – 2 год.
32. Означення функції в точці. Диференціал. Геометрична
диференціала. Інваріантність форми першого диференціалу.
- 2 год.
33. Похідні і диференціали вищих порядків. Формула Тейлора для
і формула Тейлора із залишковим членом у формі Піано і у формі
Лагранжа. – 2 год.
34. Правила Лопіталя. Опуклі функції та умови опуклості. Нерівність Ієнсена.
Точки перегину. – 2 год.
35. Необхідні та достатні умови локального екстремуму. Асимптоти графіка
функції. – 2 год.
36. Дослідження функції та побудова її графіку. – 2 год.
Лабораторна робота 22. Означення похідної та обчислення похідних. –
2 год.
Лабораторна робота 23. Обчислення похідних (продовження). – 2 год.
Лабораторна робота 24. Обчислення похідних та геометричний зміст
похідної. – 2 год.
Лабораторна робота 25. упченкованаість функції в точці.
Диференціал. – 2 год.
Лабораторна робота 26. Похідні та диференціали вищих порядків. – 2
год.
Лабораторна робота 27. Основні теореми диференціального числення.
- 2 год.
Лабораторна робота 28. Правило Лопіталя розкриття упченкова-
стей типу
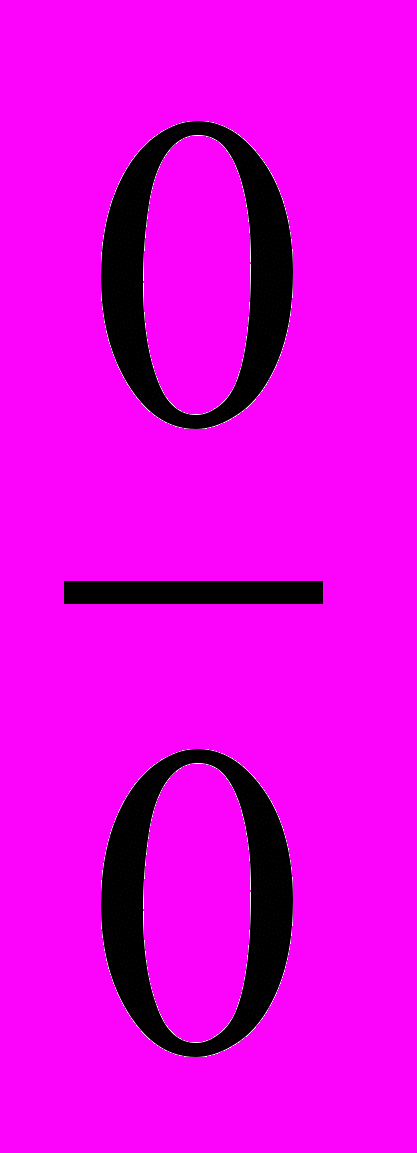 . – 2 год.
. – 2 год.Лабораторна робота 29. Правило Лопіталя розкриття упченкова-
стей типу
 . – 2 год.
. – 2 год.Лабораторна робота 30. Формула тейлора із залишковим членом у
формі Піано і у формі Лагранжа. – 2 год.
Лабораторна робота 31. Застосування формули Тейлора. – 2 год.
Лабораторна робота 32. Дослідження монотонності функції за
допомогою похідних. – 2 год.
Лабораторна робота 33. Необхідні і достатні умови локального
екстремума. – 2 год.
Лабораторна робота 34. Опуклість функції. Точки перегину. Побудова
графіків. – 2 год.
Лабораторна робота 35. Асимптоти графіка функції. Побудова графіків
функцій. – 2 год.
Лабораторна робота 36. Контрольна робота. Границя функції в точці,
неперервність, похідна та її застосування.
Побудова графіків функцій. – 2 год.
Самостійна робота – 64 год. (опрацювання лекційного матеріалу і виконання домашніх завдань).
Контрольні запитання і завдання.
- Гранична точка множини. Критерій граничної точки.
- Означення Коші границі функції в точці. Приклади.
- Означення Гейне границі функції в точці.
- Теорема про рівносильність означень границі функції в точці за Коші і за Гейне.
- Властивості границі функції в точці.
- Односторонні границі.
- Теорема про існування границі монотонної функції.
- Критерій Коші існування границі функції в точці.
- Відношення підпорядкованості “О” і його властивості.
- Відношення нехтування “о” і його властивості.
- Відношення еквівалентності і його властивості.
- Порядок однієї функції відносно другої.
- Шкала порівнянь.
- Головна частина функції відносно шкали порівнянь.
- Теорема про головної частини функції відносно шкали порівнянь. Поняття про асимптотичний розклад функції відносно шкали порівнянь.
- Означення неперервності функції в точці.
- Найпростіші властивості неперервних в точці функцій.
- Теорема про існування і неперервності оберненої функції.
- Означення і властивості логарифмічної функції.
- Означення і властивості обернених тригонометричних функцій.
- Чудові границі.
- Властивості функцій неперервних на відрізку. Перша і друга теореми Вейєрштраса.
- Теорема Коші про проміжне значення.
- Рівномірна неперервність і теорема Кантора.
- Розриви функції і їх класифікація.
- Теорема Вейєрштраса про рівномірне наближення неперервної функції многочленами.
- Похідна. Її фізична і геометрична інтерпретація.
- Правила обчислення похідних. Таблиця похідних.
- Односторонні похідні.
- Теореми Ферма, Ролля, Лагранжа і Коші. Наслідки.
- Дослідження монотонності функцій за допомогою похідних.
- Означення диференціалу. Інваріантність форми 1-го диференціалу.
- Похідні вищих порядків. Формула Лейбніца. Диференціали вищих порядків.
- Формула Тейлора із залишковим членом у формі Піано і в формі Лагранжа.
- Правила Лопиталя.
- Опуклі функції. Критерії опуклості в термінах функції нахилу, першої похідної, другої похідної. Нерівність Ієнсена.
- Точка локального екстремума. Необхідні умови. Достатні умови локального екстремума.
- Точки перегину графіка функції.
- Дослідження функцій на існування асимптот.
- Побудова графіків функцій з повним дослідженням.
Система контролю знань.
Змістовний модуль 1-21 бал:
- виконання лабораторних робіт (відвідування, активність студента на
заняттях, виконання аудиторних та домашніх занять) – 6;
- письмова контрольна робота-15
Змістовний модуль 2-16 балів:
- виконання лабораторних робіт (відвідування, активність студента на
заняттях, виконання аудиторних та домашніх занять) – 6;
- колоквіум – 10;
Змістовний модуль 3-23 бали:
- виконання лабораторних робіт (відвідування, активність студента на
заняттях, виконання аудиторних та домашніх занять) – 8;
- письмова контрольна робота –15.
Іспит – 40 балів.
Всього за семестр – 100 балів.
Мінімальна кількість балів для зарахування модульної контрольної роботи – 9 балів, для колоквіуму – 6 балів.
Кожна незарахована контрольна робота може бути переписана один раз. Колоквіум можна перескласти, якщо він був пропущений з поважної причини.
Рекомендована література.
- Дороговцев А.Я., Математичний аналіз, т.І, Київ, Либідь, 1993.
- Фихтенгольц Г.М., Курс дифференциального и интегрального иччисления, т.І, М., Наука, 1969.
- Демидович Б.П., Сборник задач и упражнений по математическому анализу, М., Наука, 1968.
- Денисьєвський М.О., Курченко О.О., Нагорний В.Н., Чайковський А.В., Навчальні завдання до практичних занять з математичного аналізу, Київ, ВПЦ Київський університет, 2002.
Затверджено на засіданні кафедри математичного аналізу
протокол № від «______» _____________ 2008 року
Завідувач кафедри
математичного аналізу І.О. Шевчук
ТЕМАТИЧНИЙ ПЛАН ЛЕКЦІЙ І ЛАБОРАТОРНИХ ЗАНЯТЬ
| № теми | Назва теми І семестр | Кількість годин | ||||
| лекції | лабораторна робота | самостійна робота | контр. Модульна робота | інші форми контролю | ||
| ЗМІСТОВИЙ МОДУЛЬ 1 | ||||||
| 1. | Елементи теорії множин та дійсні числа. | 16 | 18 | 32 | | |
ЗМІСТОВИЙ МОДУЛЬ 2 | ||||||
| 2. | Границя послідовності дійсних чисел. | 14 | 12 | 32 | | |
ЗМІСТОВИЙ МОДУЛЬ 3 | ||||||
| 3. | Границя функції в точці. Неперервні функції. | 22 | 12 | 32 | | |
| 4. | Похідна та її застосування | 20 | 30 | 32 | | |
| Всього годин за І семестр: | 72 | 72 | 128 | | | |
Методичні рекомендації по вивченню дисципліни.
Дисципліна “математичний аналіз” є базовою нормативною дисципліною для спеціальності “математика”, що читається в І, ІІ, ІІІ та ІV семестрах в обсязі 16 кркдитів (за Європейською Кредитно-Трансферною системою ECTS), і розрахована на 1056 годин занять. З них 280 годин лекцій, 280 годин лабораторних і 496 годин самостійної роботи. (І семестр: лекції – 72, лабораторні-72, самостійна робота – 128; ІІ семестр: лекції – 68, лабораторні – 68, самостійна робота – 120, ІІІ семестр: лекції – 72, лабораторні – 72, самостійна робота – 128; ІV семестр: лекції – 68, лабораторні – 68, самостійна робота – 120). Закінчується іспитами в І, ІІ, ІІІ та ІV семестрах.
Мета і завдання навчальної дисципліни “математичний аналіз” оволодіти класичними методами математичного аналізу, теоретичними положеннями та основними застосуваннями математичного аналізу в різноманітних задачах математики і механіки, їх використання в подальших курсах з математики та механіки, сприянню розвитку логічного та аналітичного мислення студентів.
Предмет навчальної дисципліни “математичний аналіз”: множини, функції, дійсні числа, послідовності, границі послідовностей, границя функції в точці, неперервні функції, похідна, диференційовність функції, диференціал, похідні і диференціали вищих порядків, локальні екстремуми, формула Тейлора, первісна, невизначений інтеграл, інтеграл Рімана, інтеграл як функція верхньої границі, числові ряди, абсолютна і умовна збіжність числового ряду, нескінченні добутки, функціональні послідовності, рівномірна збіжність функціональної послідовності, функціональні ряди, область збіжності функціонального ряду, рівномірна збіжність функціонального ряду, степеневі ряди, ряд Тейлора, функції з обмеженою варіацією, інтеграл Стілтьєса, метричні простори, збіжність в метричних просторах, відкриті та замкнені множини, повні метричні простори, сепарабельні метричні простори, компактні множини, принцип стискаючих відображень, границя функції багатьох змінних в точці, повторні границі, неперервність функції багатьох змінних, похідна за напрямком, частинні похідні, градієнт, диференційовність функцій багатьох змінних, похідні, частинні похідні та диференціали старших порядків функції багатьох змінних, формула Тейлора, локальні екстремуми функцій багатьох змінних, векторні функції, неперервність, диференційовність, матриця Якобі та якобіан, невласні інтеграли по необмеженому проміжку і від необмежених функцій, інтеграл Рімана, що залежить від параметру, невласні інтеграли, що залежать від параметру, рівномірна збіжність невласних інтегралів, що залежать від параметру, Ейлерові інтеграли, кратні інтеграли по брусу, множини вимірні за Жорданом, міра Жордана, Ейлерові інтеграли, кратні інтеграли по брусу, множини вимірні за Жорданом, міра Жордана, кратні інтеграли по вимірним множинам, формула заміни змінних, полярні, циліндричні та сферичні координати, криволінійні та поверхневі інтеграли другого роду від диференціальних форм по многовидам, формули Гріна, Остроградського-Гауса та Стокса, міра на многовидах. криволінійні та поверхневі інтеграли першого типу, ряди Фур’є, формула Фур’є, перетворення Фур’є.
Вимоги до знань та вмінь:
Знати: основні поняття математичного аналізу, зокрема: множини і дії над ними, правила де Моргана, декартів добуток множин, загальне поняття відображення або функції, поняття образу та прообразу, поняття сюр’єкції, ін’єкції та бієкції, оберненої функції, суперпозиції функцій, графіка функції, рівнопотужних множин, зліченої множини, властивості злічених множин, приклад незліченої множини, задачу про вимір довжини відрізка, означення дійсного числа, означення ірраціонального числа, порівняння дійсних чисел, числова пряма і координати точок, означення точної верхньої і точної нижньої межі числової множини, теорему про характеризацію точних меж, теорему про існування точних меж, означення арифметичних операцій над дійсними числами, означення коряня натуральної степені із додатнього числа, теорему про вкладені відрізки, нерівність Коші, нерівність Коші між середнім арифметичним і середнім геометричним, означення границі послідовності, теорему про єдиність границі, теорему про обмеженість збіжної послідовності, теорему про три послідовності, теорему про арифметичні операції над збіжними послідовностіми, теорему Штольца, поняття монотонної послідовності і теорему про існування границі монотонної послідовності, число е, підпослідовності, часткові границі послідовності, теорему про характеризацію часткової границі, теорему про існування монотонної підпослідовності, теорему Больцано-Вейєрштраса, означення верхньої і нижньої границі послідовності та теорему про їх характеризацію, означення фундаментальної послідовності та критерій Коші, означення границі функції в точці за Коші і за Гейне, тероему про рівносильність означень Коші і Гейне, односторонні границі, теорему про існування границімонотонної функції в точці, критерій Коші існування границі функції в точці, означення відношень підпорядкованості, нехтування і еквівалентності та їх властивості, означення порядка однієї функції відносно другої, означення шкали порівнянь та головні частини функції відносно шкали порівнянь,означення неперервної функції в точці і на множині, теореми про арифметичні операції над неперервними функціями, про неперервність суперпозиції, про існування і неперервність оберненої функції, першу і другу теореми Вейєрштраса та теореми про обернення неперервної функції в нуль і теорему Коші про проміжне значення, рівномірної неперервності і теорему Кантора, розриви функції в точці і їх класифікацію, теорему про розриви монотонної функції, теорему Вейєрштраса про рівномірне наближення неперервної функції многочленами, означення похідної, фізичну та геометричну інтерпретацію похідної, правила обчислення похідних, похідну від складеної та оберненої функції, поняття односторонніх похідних, теореми Ферма, Ролля, Лагранжа і Коші, теореми про монотонність і строгу монотонність на інтервалі, означення диференційовної функції в точці, критерій диференційовності, означення похідних вищих порядків, формулу Лейбніца, означення диференціалів вищих порядків, формулу Тейлора із залишковими членами в формі Піано і Лагранжа, правила Лопіталя, означення опуклої вниз на інтервалі функції, критерій опуклості в термінах похідної і похідної другого порядку, нерівність Ієнсена, точки локального екстремума функції, необхідні умови локального екстремума, достатні умови локального екстремума в термінах похідної і в термінах похідних вищих порядків, означення точок перегину і методи їх знаходження, означення асимптот графіка функції, поняття первісної та узагальненої первісної, невизначений інтеграл, таблицю невизначених інтегралів, теореми про інтегрування за допомою підстановки і за частинами, розклад раціональної функції на елементарні дроби за методом невизначених коефіцієнтів, інтегрування елементарних дробів, інтегрування раціональної функції від
 Sin і Cos, універсальна тригонометрична підстановка, інтегрування біноміальних диференціалів, підстановки Ейлера, означення верхньої та нижньої суми Дарбу і інтегральної суми,нижній і верхній інтеграл, функція інтегрована за Ріманом на відрізку, властивості сум Дарбу, критерій інтегровності, теореми про інтегровність монотонної неперервної та неперервної і обмеженої за винятком скінченного числа точок функцій, означення границі інтегральних сум, теорема Дарбу, лінійність і адитивність інтегралу Рімана, теорему про середнє значення, означення інтегралу із змінною верхньою границею, теореми про неперервність і диференційовність, теорему про існування первісної, формулу Ньютона-Лейбніца, теореми про заміну змінноїі і інтегрування за частинами у визначеному інтегралі, формулу Тейлора із залишковим членом у інтегральній формі,означення поточкової та рівномірної збіжності послідовності функцій, теорема про граничний перехід під знаком інтегралу Рімана, означення площі криволінійної трапеції і формула для її обчислення, означення довжини дуги кривої і формули для її обчислення, означення об’єму тіла обертання і формула для його обчислення, означення площі поверхні тіла обертання і формули для його обчислення, означення числового ряду, необхідні умови збіжності, геометричний ряд, гармонічний ряд, узагальнений гармонічний ряд, елементарні властивості числових рядів, критерій Коші збіжності числового ряду, критерій збіжності для числових рядів з невід’ємними членами, перша, друга й третя ознаки порівняння для рядів з невід’ємними членами, ознаки д’Аламбера, Коші, логарифмічна, Раабе і інтегральна Маклорена-Коші збіжності рядів з невід’ємними членами, ряд Лейбніца, означення абсолютної і умовної збіжності ряду, теореми про абсолютно і умовно збіжні ряди, ознака Лейбніца, Ознаки Діріхле і Абеля, теореми про групування та перестановку членів ряду, добуток рядів за Коші, нескінченні добутки, необхідні умови збіжності, зв’язок з рядами, додатні умови збіжності, поняття поточкової та рівномірної збіжності на множині функціональної послідовності, критерій Коші рівномірної збіжності, означення області збіжності функціонального ряду, означення області збіжності функціонального ряду на множині, ознаки Вейєрштраса, Діріхле та Абеля рівномірної збіжності функціональних рядів, теореми про неперервність суми, почленне інтегрування, граничний перехід і почленне диференціювання функціонального ряду, означення степеневого ряду, теорема Коші-Адамара, радіус збіжності і інтервал збіжності, теорему про рівномірну збіжність степеневого ряду, теореми про властивості сум степеневих рядів, ряд Тейлора, степеневі ряди в комплексній площині, теорема Коші-Адамара, радіус збіжності і круг збіжності,
Sin і Cos, універсальна тригонометрична підстановка, інтегрування біноміальних диференціалів, підстановки Ейлера, означення верхньої та нижньої суми Дарбу і інтегральної суми,нижній і верхній інтеграл, функція інтегрована за Ріманом на відрізку, властивості сум Дарбу, критерій інтегровності, теореми про інтегровність монотонної неперервної та неперервної і обмеженої за винятком скінченного числа точок функцій, означення границі інтегральних сум, теорема Дарбу, лінійність і адитивність інтегралу Рімана, теорему про середнє значення, означення інтегралу із змінною верхньою границею, теореми про неперервність і диференційовність, теорему про існування первісної, формулу Ньютона-Лейбніца, теореми про заміну змінноїі і інтегрування за частинами у визначеному інтегралі, формулу Тейлора із залишковим членом у інтегральній формі,означення поточкової та рівномірної збіжності послідовності функцій, теорема про граничний перехід під знаком інтегралу Рімана, означення площі криволінійної трапеції і формула для її обчислення, означення довжини дуги кривої і формули для її обчислення, означення об’єму тіла обертання і формула для його обчислення, означення площі поверхні тіла обертання і формули для його обчислення, означення числового ряду, необхідні умови збіжності, геометричний ряд, гармонічний ряд, узагальнений гармонічний ряд, елементарні властивості числових рядів, критерій Коші збіжності числового ряду, критерій збіжності для числових рядів з невід’ємними членами, перша, друга й третя ознаки порівняння для рядів з невід’ємними членами, ознаки д’Аламбера, Коші, логарифмічна, Раабе і інтегральна Маклорена-Коші збіжності рядів з невід’ємними членами, ряд Лейбніца, означення абсолютної і умовної збіжності ряду, теореми про абсолютно і умовно збіжні ряди, ознака Лейбніца, Ознаки Діріхле і Абеля, теореми про групування та перестановку членів ряду, добуток рядів за Коші, нескінченні добутки, необхідні умови збіжності, зв’язок з рядами, додатні умови збіжності, поняття поточкової та рівномірної збіжності на множині функціональної послідовності, критерій Коші рівномірної збіжності, означення області збіжності функціонального ряду, означення області збіжності функціонального ряду на множині, ознаки Вейєрштраса, Діріхле та Абеля рівномірної збіжності функціональних рядів, теореми про неперервність суми, почленне інтегрування, граничний перехід і почленне диференціювання функціонального ряду, означення степеневого ряду, теорема Коші-Адамара, радіус збіжності і інтервал збіжності, теорему про рівномірну збіжність степеневого ряду, теореми про властивості сум степеневих рядів, ряд Тейлора, степеневі ряди в комплексній площині, теорема Коші-Адамара, радіус збіжності і круг збіжності, показникова функція в комплексній площині, теорему про рохзклад монотонної функції на неперервну монотонну функцію і функцію стрибків, означення функції обмеженої варіації, елементарні властивості функції обмеженої варіації, теорема Жордана, верхня і нижня суми Дарбу-Стилтьєса, верхній і нижній інтеграли Рімана-Стілтьєса, означення функції інтегровної відносно монотонно не спадної функції на відрізку за Ріманом-Стілтьєсом, властивості інтеграла Стілтьєса, інтеграл Стілтьєса відносно функції обмеженої варіації, обчислення інтегралу Стілтьєса, теорема Хелі, означення метричного простору, приклади метричних просторів, властивості метрики – нерівності трикутника і чотирикутника, декартовий добуток метричних просторів, збіжність послідовності елементів метричного простору, теорему про єдиність границі, збіжність в
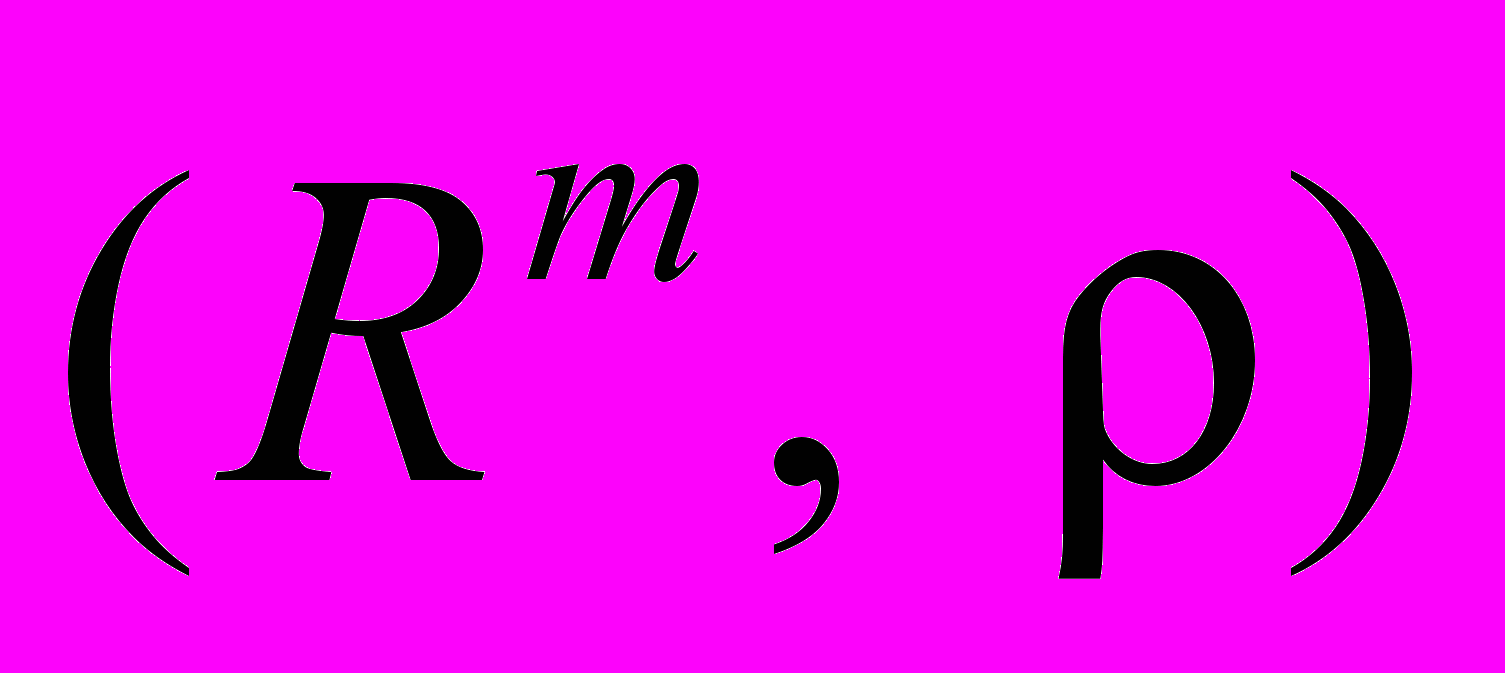 і
і 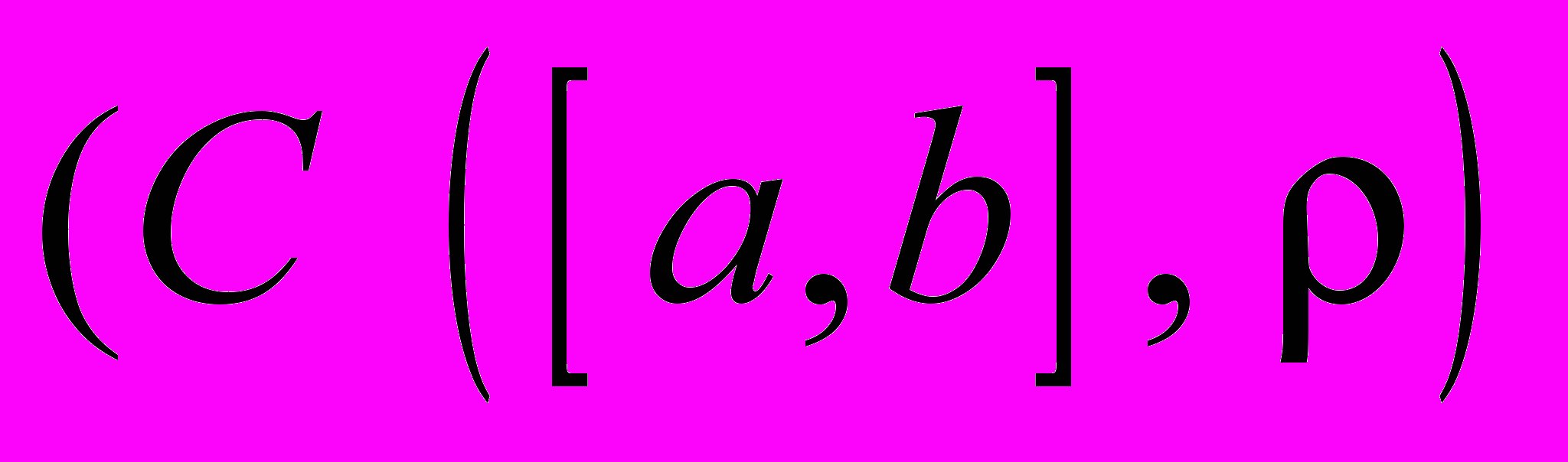 , граничні точки множини і критерій граничної точки, відкриті і замкнені множини в метричному просторі та їх властивості, теореми про структуру відкритих множин на прямій і в просторі
, граничні точки множини і критерій граничної точки, відкриті і замкнені множини в метричному просторі та їх властивості, теореми про структуру відкритих множин на прямій і в просторі 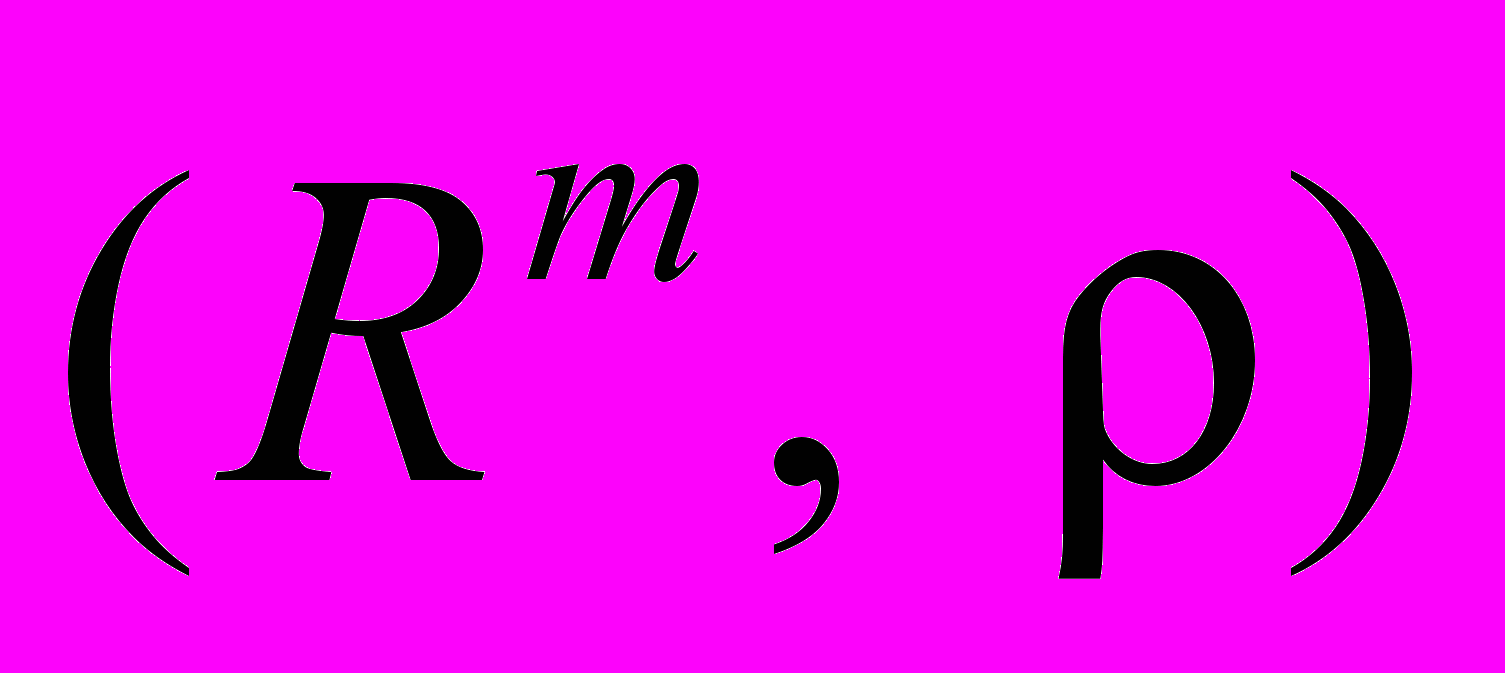 ,критерій замкненості, сепарабельні метричні простори, повні метричні простори, повноту просторів
,критерій замкненості, сепарабельні метричні простори, повні метричні простори, повноту просторів 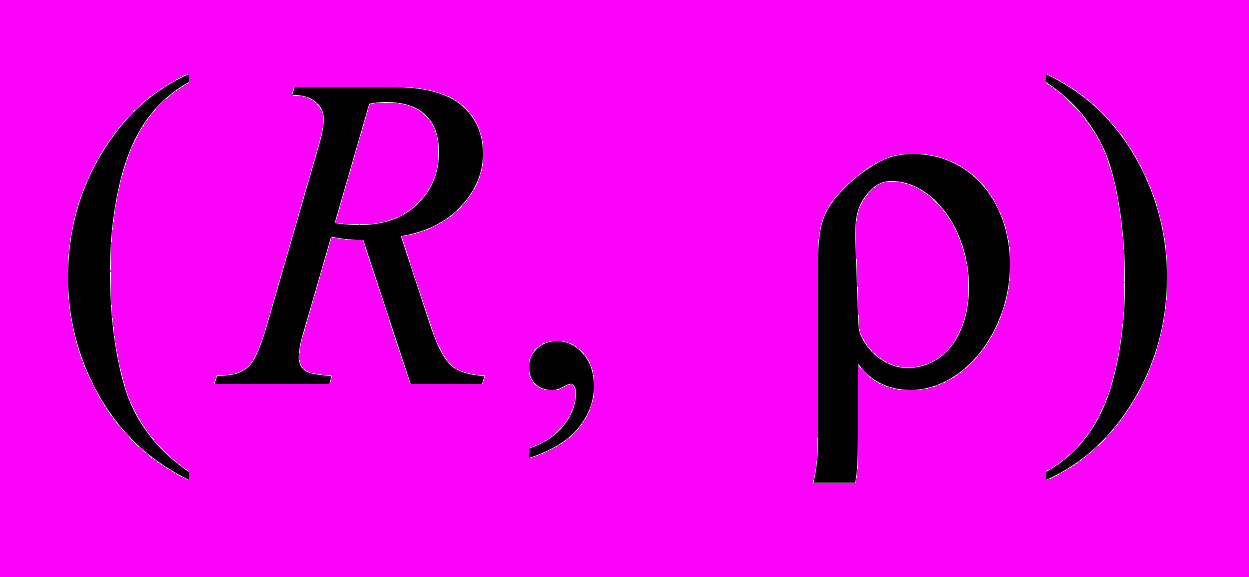 ,
, 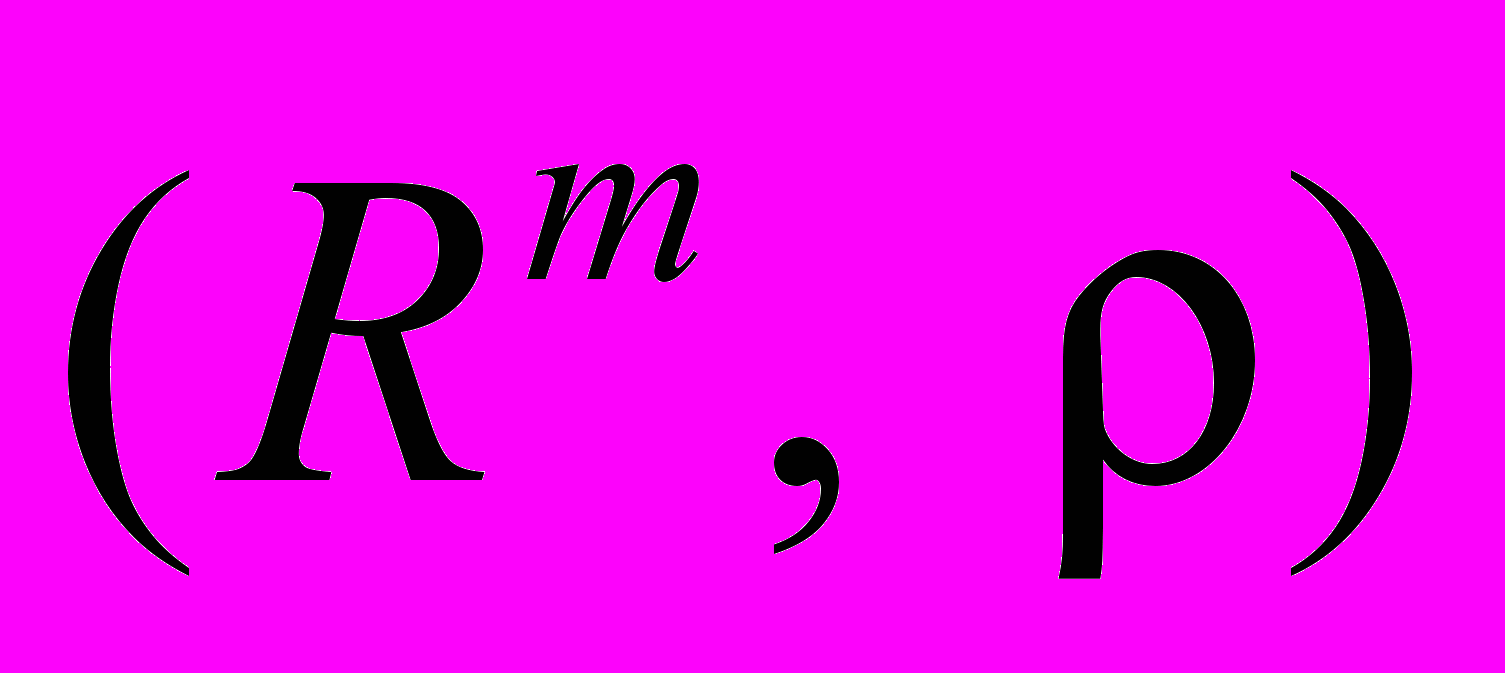 ,
,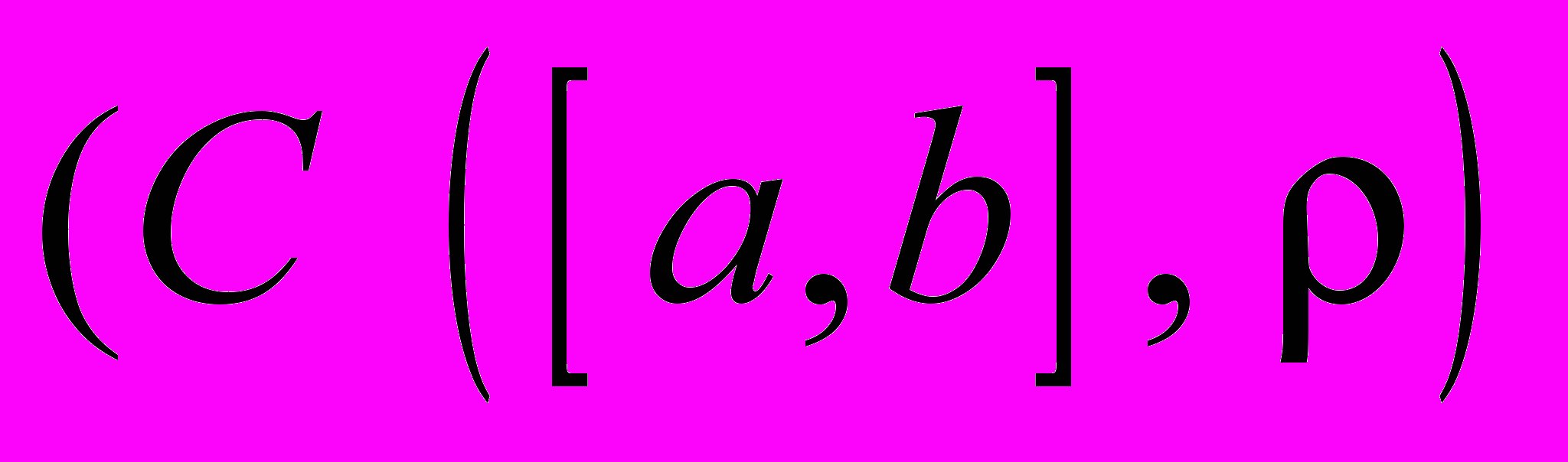 , теорему про вкладені замкнені кулі, ізометричні метричні простори, теорему про поповнення (формулювання), функції на метричних просторах, границю функції в точці, теорему про єдиність границі, неперервність функції в точці і на множині, теорему про неперервність векторної функції, теорему про неперервність складної функції, теорему про характеризацію неперервності, рівномірно неперервні на множиніфункції, означення компактної множини, обмеженість і замкненість компактної множини, узагальнення теореми Больцано-Вейєрштраса, критерій компактності Хаусдорфа, компактні множини в
, теорему про вкладені замкнені кулі, ізометричні метричні простори, теорему про поповнення (формулювання), функції на метричних просторах, границю функції в точці, теорему про єдиність границі, неперервність функції в точці і на множині, теорему про неперервність векторної функції, теорему про неперервність складної функції, теорему про характеризацію неперервності, рівномірно неперервні на множиніфункції, означення компактної множини, обмеженість і замкненість компактної множини, узагальнення теореми Больцано-Вейєрштраса, критерій компактності Хаусдорфа, компактні множини в 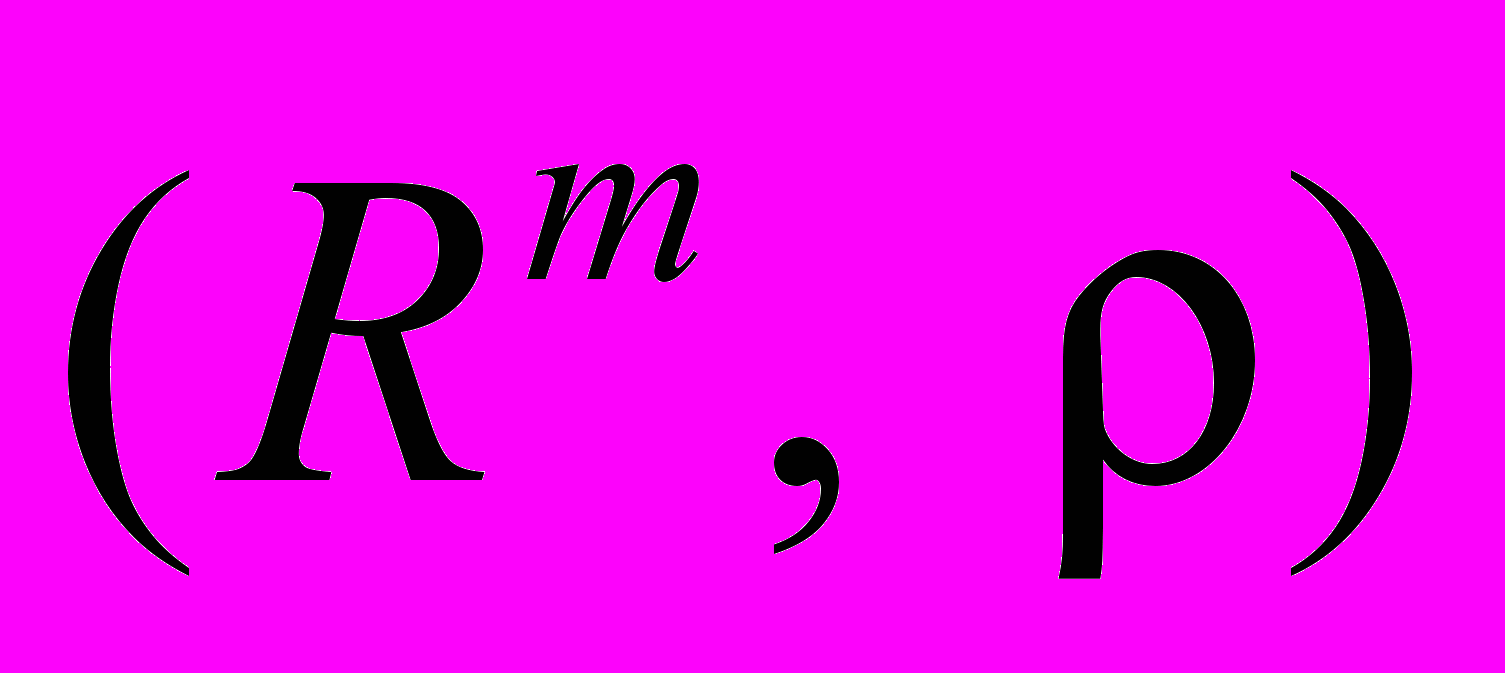 і в
і в 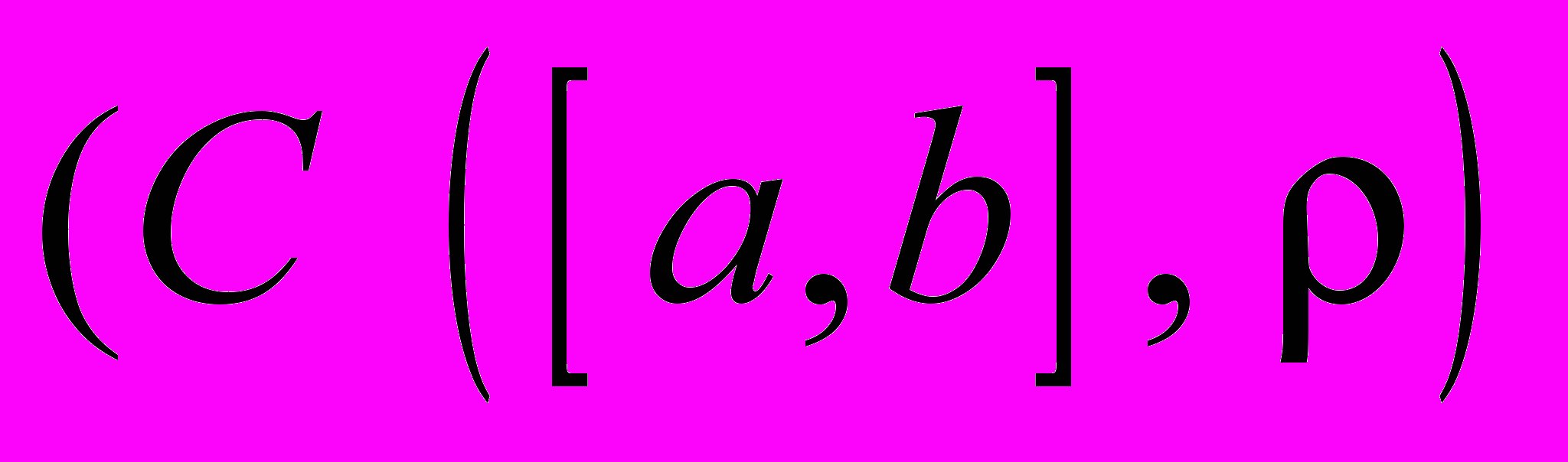 , теореми про компактність образу при неперервному відображенні, узагальнення теорем Вейєрштраса, теорему про неперервність оберненого відображення, теорему Кантора, теорему про зв’язність образу при неперервному відображенні, теорему Банаха, застосування теореми Банаха до доведення існування і єдиності розв’язку алгебраїчних рівнянь, систем лінійних рівнянь, диференціальних і інтегральних рівнянь фредгольма другого роду та теореми про неявну функцію, теорему Стоуна-Вейєрштраса (формулювання), похідну за напрямком, частинні похідні, теорему про обчислення похідної за напрямком, градієнт, означення диференційовної функції декількох змінних, властивості диференційовних функцій, достатні умови диференційовності, першу теорему про диференційовність складної функції, похідну вищого порядку за напрямками, частинні похідні вищих порядків, диференціали вищих порядків, формула Тейлора для функцій декількох змінних, локальні екстремуми функцій декількох змінних, необхідні умови локального екстремума, достатні умови локального екстремума, достатні умови локального екстремума для функцій двох змінних, означення диференційовності векторної функції декількох змінних, матриця Якобі, якобіан, правило диференціювання складного відображення, наслідок для якобіанів, лема про гомеоморфізм, теореми про існування і властивості неявної та оберненої функції, означення локального відносного екстремума, достатні умови локального відносного екстремума, екстремуми квадратичної форми на сфері, означення невласного інтегралу по нескінченному проміжку, властивості невласних інтегралів, критерій Коші збіжності невласних інтегралів, критерій збіжності невласних інтегралів від невід’ємної функції, абсолютно і умовно збіжні невласні інтеграли, ознаки Діріхле і Абеля, невласні інтеграли від необмежених функцій, інтеграл Рімана що залежить від параметру, теореми про неперервність, інтегровність і диференційовність інтеграла по параметру, рівномірна збіжність сімейства функцій, теорему про граничний перехід під знаком інтегралу що залежить від параметру, означення рівномірної збіжності невласного інтегралу що залежить від параметру, ознаки Вейєрштраса, Діріхле та Абеля рівномірної збіжності, теореми про неперервність,граничний перехід, інтегровність, диференційовність невласного інтегралу що залежить від параметру,інтеграл Діріхле, інтеграли Фрулані, теорему про інтегрування по нескінченному проміжку, інтеграл Ейлера-Пуассона, невласні інтеграли що залежать від параметру від необмежених функцій, Г-функція і її найпростіші властивості, графік Г-функції, основна теорема теорії Г-функції, формули Ейлера, Вейєрштраса, поєднання Лежандра для Г-функції, функціональне рівняння Ейлера для Г-функції, розклад сінуса в нескінченний добуток, В-функція, зв’язок між В та Г функціями, формула Стірлінга (формулювання), бруси в
, теореми про компактність образу при неперервному відображенні, узагальнення теорем Вейєрштраса, теорему про неперервність оберненого відображення, теорему Кантора, теорему про зв’язність образу при неперервному відображенні, теорему Банаха, застосування теореми Банаха до доведення існування і єдиності розв’язку алгебраїчних рівнянь, систем лінійних рівнянь, диференціальних і інтегральних рівнянь фредгольма другого роду та теореми про неявну функцію, теорему Стоуна-Вейєрштраса (формулювання), похідну за напрямком, частинні похідні, теорему про обчислення похідної за напрямком, градієнт, означення диференційовної функції декількох змінних, властивості диференційовних функцій, достатні умови диференційовності, першу теорему про диференційовність складної функції, похідну вищого порядку за напрямками, частинні похідні вищих порядків, диференціали вищих порядків, формула Тейлора для функцій декількох змінних, локальні екстремуми функцій декількох змінних, необхідні умови локального екстремума, достатні умови локального екстремума, достатні умови локального екстремума для функцій двох змінних, означення диференційовності векторної функції декількох змінних, матриця Якобі, якобіан, правило диференціювання складного відображення, наслідок для якобіанів, лема про гомеоморфізм, теореми про існування і властивості неявної та оберненої функції, означення локального відносного екстремума, достатні умови локального відносного екстремума, екстремуми квадратичної форми на сфері, означення невласного інтегралу по нескінченному проміжку, властивості невласних інтегралів, критерій Коші збіжності невласних інтегралів, критерій збіжності невласних інтегралів від невід’ємної функції, абсолютно і умовно збіжні невласні інтеграли, ознаки Діріхле і Абеля, невласні інтеграли від необмежених функцій, інтеграл Рімана що залежить від параметру, теореми про неперервність, інтегровність і диференційовність інтеграла по параметру, рівномірна збіжність сімейства функцій, теорему про граничний перехід під знаком інтегралу що залежить від параметру, означення рівномірної збіжності невласного інтегралу що залежить від параметру, ознаки Вейєрштраса, Діріхле та Абеля рівномірної збіжності, теореми про неперервність,граничний перехід, інтегровність, диференційовність невласного інтегралу що залежить від параметру,інтеграл Діріхле, інтеграли Фрулані, теорему про інтегрування по нескінченному проміжку, інтеграл Ейлера-Пуассона, невласні інтеграли що залежать від параметру від необмежених функцій, Г-функція і її найпростіші властивості, графік Г-функції, основна теорема теорії Г-функції, формули Ейлера, Вейєрштраса, поєднання Лежандра для Г-функції, функціональне рівняння Ейлера для Г-функції, розклад сінуса в нескінченний добуток, В-функція, зв’язок між В та Г функціями, формула Стірлінга (формулювання), бруси в 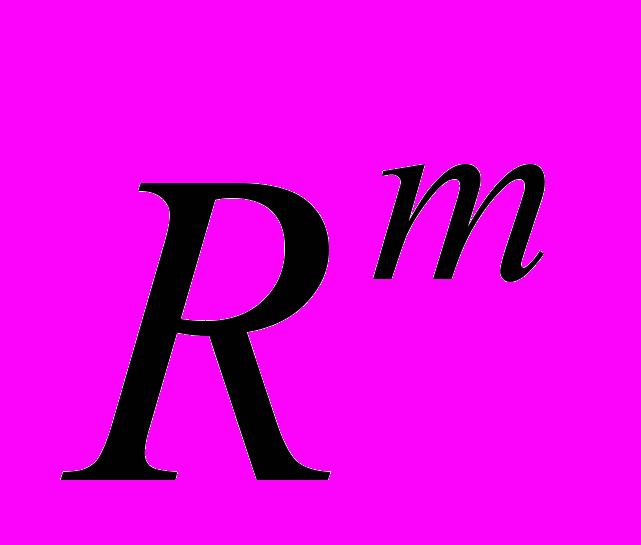 , діаметр і міра бруса, розбиття і підрозбиття бруса, суми Дарбу і їх властивості, інтегральні суми, верхній і нижній інтеграли для обмеженої функції, функція інтегровна по брусу, кратний інтеграл від функції по брусу, критерій інтегровності, інтегровність неперервної функції по брусу, найпростіші властивості кратних інтегралів по брусу, формула зведення кратного інтеграла до послідовних однократних, внутрішня і зовнішня міра обмеженої множини, вимірні за Жорданом множини і міра Жордана, властивості вимірних множин і міра Жордана, циліндричні множини і теорема про їх вимірність, означення кратного інтегралу по вимірній множині, обчислення інтегралів по циліндричним множинам, відображення спеціального виду, вимірність образу при відображенні спеціального виду, формула заміни змінних при відображенні спеціального виду, лема про зведення загального відображення до суперпозицій відображень спеціального виду, формула заміни змінних, поняття невласних кратних інтегралів від необмежених функцій та по необмеженим множинам, допустимі координатні простори та орієнтація, диференціальні форми степені m в просторі
, діаметр і міра бруса, розбиття і підрозбиття бруса, суми Дарбу і їх властивості, інтегральні суми, верхній і нижній інтеграли для обмеженої функції, функція інтегровна по брусу, кратний інтеграл від функції по брусу, критерій інтегровності, інтегровність неперервної функції по брусу, найпростіші властивості кратних інтегралів по брусу, формула зведення кратного інтеграла до послідовних однократних, внутрішня і зовнішня міра обмеженої множини, вимірні за Жорданом множини і міра Жордана, властивості вимірних множин і міра Жордана, циліндричні множини і теорема про їх вимірність, означення кратного інтегралу по вимірній множині, обчислення інтегралів по циліндричним множинам, відображення спеціального виду, вимірність образу при відображенні спеціального виду, формула заміни змінних при відображенні спеціального виду, лема про зведення загального відображення до суперпозицій відображень спеціального виду, формула заміни змінних, поняття невласних кратних інтегралів від необмежених функцій та по необмеженим множинам, допустимі координатні простори та орієнтація, диференціальні форми степені m в просторі 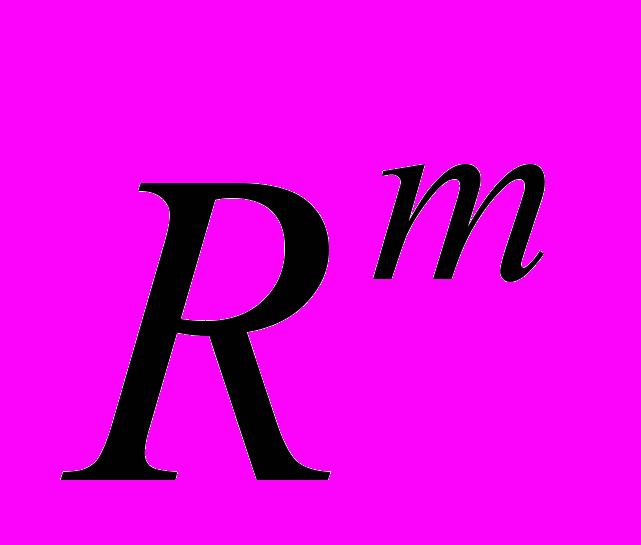 , орієнтована крива, орієнтована поверхня, диференціальні форми степені p в пpосторі
, орієнтована крива, орієнтована поверхня, диференціальні форми степені p в пpосторі 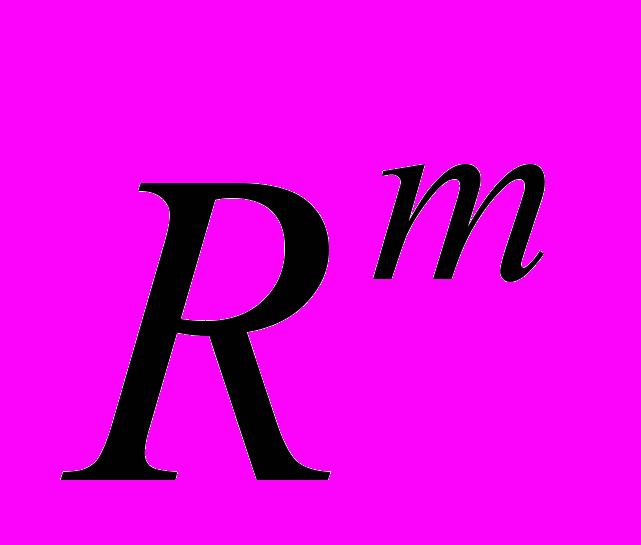 , канонічна форма диференціальної форми, інтеграл від диференціальної форми степеня по орієнтованому многовиду вимірності p в пpосторі
, канонічна форма диференціальної форми, інтеграл від диференціальної форми степеня по орієнтованому многовиду вимірності p в пpосторі 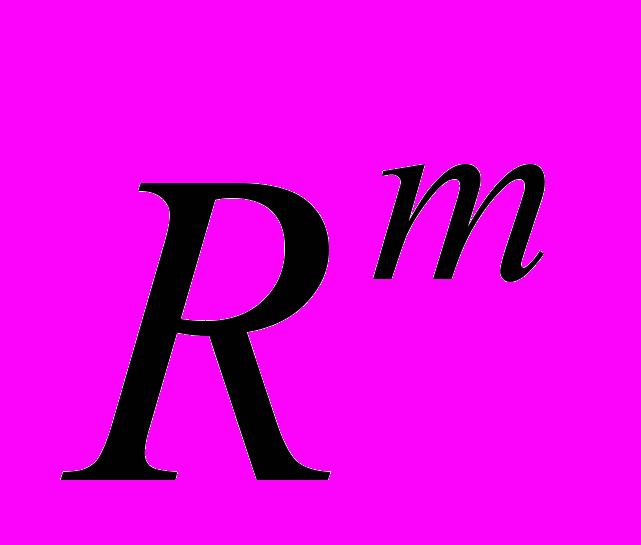 , криволінійний інтеграл другого роду, криволінійний інтеграл другого роду як границя інтегральних сум, поверхневий інтеграл другого роду, зовнішній диференціал диференціальної форми, теорема Пуанкаре, орієнтація границі множини що відповідає орієнтації множини, формула Стокса в спеціальному випадку, загальна формула Стокса, формула Гріна, Остроградського-Гауса та Стокса, точні диференціальні форми, замкнені диференціальні форми, однозв’язні множини, теорему про незалежність криволінійного інтегралу другого роду від шляху інтегрування, означення міри на многовиді, довжина дуги кривої, площа поверхні, означення інтегралу першого роду від функції по многовиду, зв’язок інтегралів першого і другого роду по многовидам, криволінійний інтеграл першого роду, поверхневий інтеграл першого роду, клас
, криволінійний інтеграл другого роду, криволінійний інтеграл другого роду як границя інтегральних сум, поверхневий інтеграл другого роду, зовнішній диференціал диференціальної форми, теорема Пуанкаре, орієнтація границі множини що відповідає орієнтації множини, формула Стокса в спеціальному випадку, загальна формула Стокса, формула Гріна, Остроградського-Гауса та Стокса, точні диференціальні форми, замкнені диференціальні форми, однозв’язні множини, теорему про незалежність криволінійного інтегралу другого роду від шляху інтегрування, означення міри на многовиді, довжина дуги кривої, площа поверхні, означення інтегралу першого роду від функції по многовиду, зв’язок інтегралів першого і другого роду по многовидам, криволінійний інтеграл першого роду, поверхневий інтеграл першого роду, клас 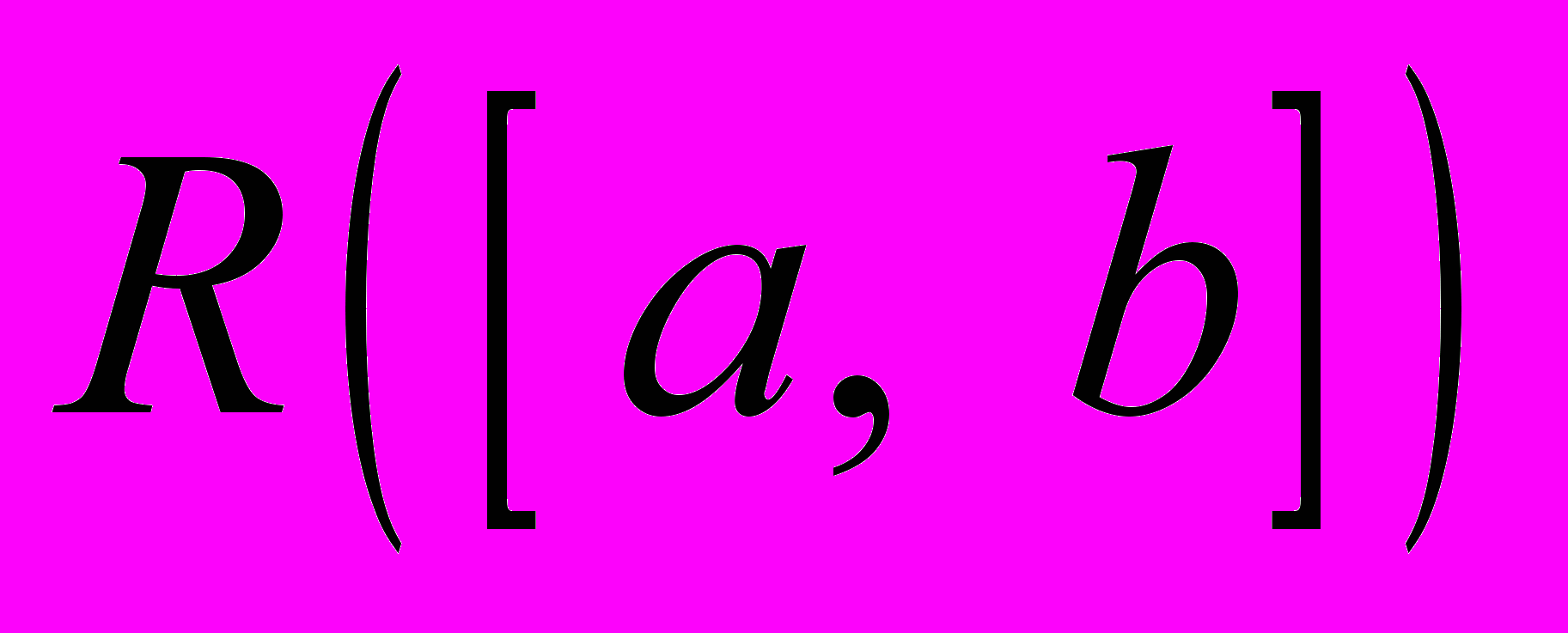 , скалярний добуток, норма функції, середньоквадратична віддаль між функціями, ортонормовані послідовності, лінійно-незалежні послідовностіфункцій, коефіцієнти Фур’є і ряд Фур’є функції по ортонормованій послідовності, нерівність Бесселя, замкнені послідовності функцій, степенева послідовність замкнена на будь якому відрізку, тригонометрична послідовність замкнена на будь якому відрізку довжиною 2
, скалярний добуток, норма функції, середньоквадратична віддаль між функціями, ортонормовані послідовності, лінійно-незалежні послідовностіфункцій, коефіцієнти Фур’є і ряд Фур’є функції по ортонормованій послідовності, нерівність Бесселя, замкнені послідовності функцій, степенева послідовність замкнена на будь якому відрізку, тригонометрична послідовність замкнена на будь якому відрізку довжиною 2 , теорему про середньоквадратичну збіжність ряду Фур’є, клас
, теорему про середньоквадратичну збіжність ряду Фур’є, клас 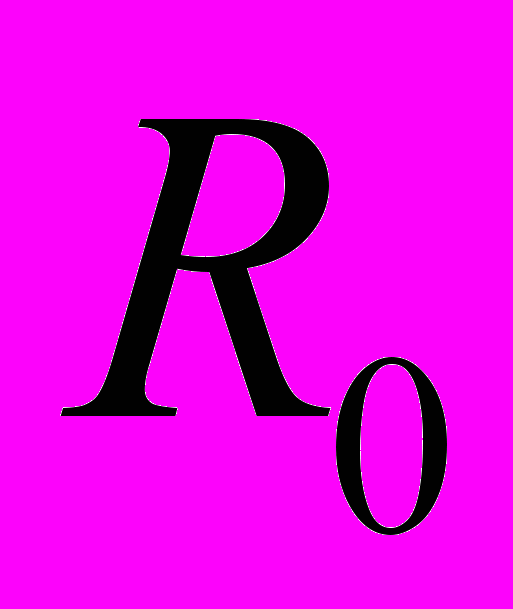 , ряд Фур’є по тригонометричній послідовності функцій, лему Рімана, інтегральне зображення часткових сум ряду Фур’є, критерій збіжності ряду Фур’є в точці, ознаки Діні і Ліпшиця поточкової збіжності ряду Фур'є, теорему Фейєра, поняття тригометричного ряду, теорема про рівномірно збіжний на прямій тригонометричний ряд, теорема про рівномірну збіжність ряду Фур’є, теореми про почленне інтегрування та диференціювання ряду Фур’є, розклад в ряд Фур’є функцій з довільним періодом, поняття про інтеграл Фур’є, ознаки Діні і Ліпшиця збіжності інтеграла Фур’є в точці, поняття про перетворення Фур’є, формула обертання.
, ряд Фур’є по тригонометричній послідовності функцій, лему Рімана, інтегральне зображення часткових сум ряду Фур’є, критерій збіжності ряду Фур’є в точці, ознаки Діні і Ліпшиця поточкової збіжності ряду Фур'є, теорему Фейєра, поняття тригометричного ряду, теорема про рівномірно збіжний на прямій тригонометричний ряд, теорема про рівномірну збіжність ряду Фур’є, теореми про почленне інтегрування та диференціювання ряду Фур’є, розклад в ряд Фур’є функцій з довільним періодом, поняття про інтеграл Фур’є, ознаки Діні і Ліпшиця збіжності інтеграла Фур’є в точці, поняття про перетворення Фур’є, формула обертання.Вміти: виконувати операції над множинами, обчислювати границі послідовностей, обчислювати границю функцій в точках, досліджувати функції на неперервність, обчислювати похідну функції, досліджувати функції за допомогою похідних, обчислювати невизначені інтеграли, обчислювати інтеграли Рімана, застосовувати інтеграл Рімана до знаходження площ плоських фігур, довжин дуг кривих, об’ємів тіл обертання, площ поверхонь тіл обертання, знаходження координат центрів ваги, досліджувати на абсолютну та умовну збіжність числові ряди, досліджувати на рівномірну збіжність функціональні послідовності і функціональні ряди, досліджувати властивості сум функціональних рядів, розкладати функції в степеневі ряди, обчислювати інтеграли Стілтьєса, досліджувати функції задані на метричних просторах, застосовувати принцип стискуючих відображеньт до задач в різних галузях математики, знаходити границі функцій багатьох змінних в точках, знаходити поверхневі границі, обчислювати похідні за напрямком і частинні похідні, досліджувати функції багатьох змінних на локальні екстремуми та умовні екстремуми. Обчислювати матриці Якобі та якобіани відображень, застосовувати теореми про існування і властивості обернених і неявних відображень, досліджувати невласні інтеграли на збіжність, та невласні інтеграли що залежать від параметру на рівномірну збіжність, досліджувати функціональні властивості невласних інтегралів що залежать від параметру, обчислювати кратні інтеграли, використовувати формулу заміни змінних, обчислювати криволінійні і поверхневі інтеграли другого типу від диференціальних форм, користуватися формулами Гріна, Остроградського-Гауса та Стокса, розкладати функції в ряди Фур’є та досліджувати їх збіжність, користуватися інтегралом Фур’є та перетворенням Фур’є.
Місце в структурно-логічній схемі спеціальності.
Нормативно-навчальна дисципліна “математичний аналіз” є складовою циклу професійної підготтовки фахівців освітньо-кваліфікаційного рівня “бакалавр”, і базовою для вивчення спеціальних дисциплін “аналітична геометрія”, “диференціальні рівняння”, “диференціальна геометрія”, “теорія функцій комплексної змінної”, “математична фізика”, “теорія міри”, “функціональний аналіз”, “теоретична механіка” та інших.
