Geum.ru

Робоча навчальна програма дисципліни для студентів спеціальності «механіка» та «математика» Затверджено вченою радою факультету

Вид материалаДокументы

Содержание


МАТЕМАТИЧНИЙ АНАЛІЗ (І курс, ІІ семестр)Робоча навчальна програма дисципліни
Затверджено вченою радою факультету
Подобный материал:

Київський національний університет імені Тараса Шевченка

Механіко-математичний факультет

Кафедра математичного аналізу

“Затверджую”


декан механіко-математичного


факультету, проф. __________


Викладачі

кандидат фізико-математичних наук, доцент

Денисьєвський Микола Олексійович

кандидат фізико-математичних наук, доцент

Курченко Олександр Олексійович

кандидат фізико-математичних наук, доцент

Чайковський Андрій Володимирович

МАТЕМАТИЧНИЙ АНАЛІЗ


(І курс, ІІ семестр)

Робоча навчальна програма дисципліни


для студентів спеціальності «механіка» та «математика»


Затверджено

вченою радою факультету


“_____” ____________

протокол № _________





Змістовий модуль 1


Тема 1. Невизначений інтеграл.


  1. Первісна. Узагальнена первісна. Невизначений інтеграл. Геометрична інтерпретація невизначеного інтегралу і його найпростіші властивості. Таблиця невизначених інтегралів. – 2 год.
  2. Інтегрування за допомогою заміни змінної та інтегрування за частинами в невизначеному інтегралі. – 2 год.
  3. Інтегрування раціональних функцій. Розклад раціональних функцій на елементарні дроби. Метод невизначених коефіцієнтів. – 2 год.
  4. Інтегрування елементарних дробів. – 2 год.
  5. Інтегрування функції виду



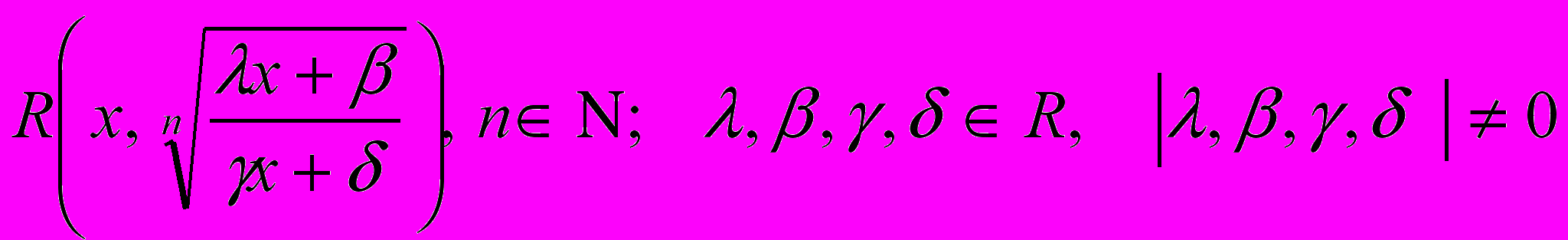
Інтегрування квадратичних ірраціональностей за допомогою підстановок Ейлера. – 2 год.
  1. Інтегрування біноміальних диференціалів та раціональних функцій від тригонометричних функцій. Універсальна тригонометрична підстановка. – 2 год.



Лабораторна робота 1. Означення первісної та невизначеного інтегралу. Узагальнена первісна. Таблиця основних інтегралів. – 2 год.

Лабораторна робота 2. Знаходження невизначених інтегралів за допомо-

гою таблиці основних інтегралів та їх елементарних власти-

востей. – 2 год.

Лабораторна робота 3. Інтегрування за допомогою підстановки. – 2 год.

Лабораторна робота 4. Інтегрування за частинами. – 2 год.

Лабораторна робота 5. Інтегрування раціональних функцій. – 2 год.

Лабораторна робота 6. Інтегрування ірраціональних функцій. – 2 год.

Лабораторна робота 7. Інтегрування тригонометричних функцій. – 2 год.

Лабораторна робота 8. Різні прийоми інтегрування. – 2 год.

Лабораторна робота 9. Контрольна робота на основні методи обчислення

інтегралів. – 2 год.


Самостійна робота – 30 год. (опрацювання лекційного матеріалу і виконання домашніх завдань).


Контрольні запитання і завдання.
  1. Означення первісної та узагальненої первісної.
  2. Неоднозначність визначення первісної.
  3. Невизначений інтеграл та його найпростіші властивості.
  4. Таблиця основних інтегралів.
  5. Інтегрування за допомогою підстановки.
  6. Правило інтегрування за частинами.
  7. Інтегрування раціональних функцій. Розклад раціональних функцій на елементарні дроби.
  8. Метод невизначених коефіцієнтів.
  9. Метод Остроградського.
  10. Інтегрування елементарних дробів.
  11. Інтегрування функцій виду


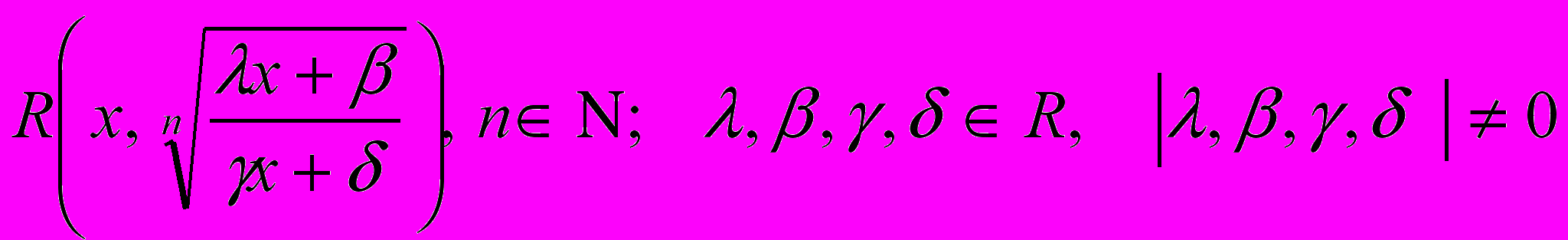
  1. Інтегрування квадратичних ірраціональностей. Три підстановки Ейлера.
  2. Інтегрування біноміальних диференціалів.
  3. Інтегрування функцій виду ,

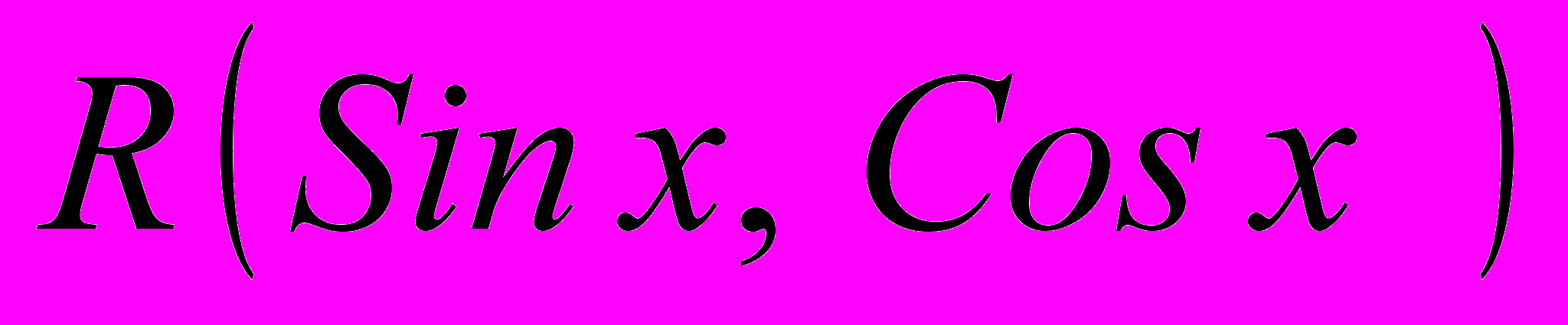універсальна тригонометрична підстановка.
  1. Різні випадки інтегрування тригонометричних функцій.



Змістовий модуль 2.


Тема 2. Інтеграл Рімана. Застосування інтеграла Рімана.

  1. Інтегровні на відрізку функції та означення інтеграла Рімана. – 2 год.
  2. Критерій інтегрованості. – 2 год.
  3. Класи інтегровних за Ріманом функцій. – 2 год.
  4. Інтеграл Рімана, як границя інтегральних сум. Теорема Дарбу. – 2 год.
  5. Властивості інтеграла Рімана. – 2 год.
  6. Інтеграл, як функція верхньої границі інтегрування. Основна формула інтегрального числення, або формула Ньютона-Лейбніца. – 2 год.
  7. Формула заміни змінної у інтегралі Рімана та формула інтегрування за частинами у інтегралі Рімана. Граничний перехід під знаком інтегралу Рімана. – 2 год.
  8. Обчислення площі плоських фігур, обчислення довжини дуги кривої. – 2 год.
  9. Обчислення об’ємів тіл обертання та площі поверхонь тіл обертання. – 2 год.


Лабораторна робота 10. Означення інтеграла Рімана. Критерій інтегров-

ності. – 2 год.

Лабораторна робота 11. Інтеграл як границя інтегральних сум. Теорема

Дарбу. – 2 год.

Лабораторна робота 12. Властивості визначеного інтеграла. Формула

Ньютона-Лейбніца. – 2 год.

Лабораторна робота 13. Інтегрування за частинами. Заміна змінної у

інтегралі Рімана. – 2 год.

Лабораторна робота 14. Обчислення площ. Обчислення довжини дуги

кривої. – 2 год.

Лабораторна робота 15. Обчислення об’ємів та площ поверхонь тіл

обертання. Теореми Гюльдена.

Самостійна робота – 30 год. (опрацювання лекційного матеріалу і виконання домашніх завдань).


Контрольні запитання і завдання.
  1. Поняття розбиття відрізка та діаметра розбиття.
  2. Означення нижньої, верхньої сум Дарбу та інтегральної суми для функції обмеженої на відрізку.
  3. Властивості сум Дарбу та інтегральних сум.
  4. Означення нижнього та верхнього інтегралів.
  5. Означення функції інтегровного за Ріманом і інтеграла Рімана.
  6. Критерій інтегрованості. Класи інтегрованих функцій.
  7. Інтеграл як границя інтегральних сум. Теорема Дарбу.
  8. Використання теореми Дарбу для обчислення інтегралів Рімана і границь послідовностей.
  9. Властивості інтеграла Рімана. Теорема про середнє, нерівність Коші для інтегралів.
  10. Інтеграл як функція верхньої границі інтегрування. Властивості. Теорема про існування первісної.
  11. Основна формула інтегрального числення, або формула Ньютона-Лейбніца.
  12. Обчислення площі криволінійної трапеції.
  13. Обчислення площі криволінійного сектора.
  14. Обчислення довжини дуги кривої.
  15. Обчислення об’ємів тіл обертання.
  16. Обчислення площ поверхонь тіл обертання.
  17. Обчислення координат центрів ваги для матеріальних кривих, фігур на площині та тіл в просторі.
  18. Перша і друга теореми Гюльдена.



Змістовий модуль 3.


Тема 3. Числові ряди і добутки.

  1. Означення числового ряду. Необхідні умови збіжності. Приклади. Елементарні властивості збіжних рядів. – 2 год.
  2. Ряди з невід’ємними членами. Критерій збіжності. Теореми порівняння для рядів з невід’ємними членами. – 2 год.
  3. Ознаки Д’аламбера, Коші, логарифмічна та Раабе збіжності рядів з невід’ємними членами. – 2 год.
  4. Інтегральна ознака Маклорена-Коші збіжності рядів з невід’ємними членами. – 2 год.
  5. Ряди з довільними членами. Ряд Лейбніца. Абсолютно і умовно збіжні ряди. Властивості абсолютно збіжних рядів. – 2 год.
  6. Ознаки Лейбніца, Діріхле та Абеля збіжності рядів. Властивості збіжних рядів. – 2 год.
  7. Добуток рядів за Коші. Теорема про добуток двох абсолютно збіжних рядів. – 2 год.
  8. Нескінченні добутки. Необхідна та достатні умови збіжності нескінченних добутків. – 2 год.


Лабораторна робота 16. Числові ряди. Необхідні умови збіжності.

Критерій збіжності ряду з невід’ємними членами. – 2 год.

Лабораторна робота 17. Збіжність рядів з невід’ємними членами.

Ознаки збіжності. – 2 год.

Лабораторна робота 18. Абсолютно та умовно збіжні ряди. Ознаки

Лейбніца, Діріхле та Абеля. – 2 год.

Лабораторна робота 19. Властивості збіжних рядів. Добуток рядів. – 2 год.

Лабораторна робота 20. Нескінченні добутки та їх збіжність. – 2 год.


Тема 4. Функціональні ряди.

  1. Рівномірна збіжність функціональної послідовності. Критерій Коші рівномірної збіжності. Рівномірна збіжність функціонального ряду. – 2 год.
  2. Ознаки Вейєрштрасса, Діріхле та Абеля рівномірної збіжності функціональних рядів. – 2 год.
  3. Властивості рівномірно збіжних функціональних рядів. – 2 год.
  4. Степеневі ряди. Радіус збіжності степеневого ряду. Теорема Коші-Адамара. – 2 год.
  5. Область рівномірної збіжності степеневого ряду. Властивості сум степеневих рядів. – 2 год.
  6. Розклад функцій в степеневі ряди. Ряд Тейлора. – 2 год.
  7. Степеневі ряди з комплексними членами. Область збіжності. Формули Ейлера. – 2 год.


Лабораторна робота 21. Поточкова і рівномірна збіжність функціональної

послідовності. Геометрична інтерпретація. – 2 год.

Лабораторна робота 22. Множина збіжності функціонального ряду.

Рівномірна збіжність функціонального ряду. – 2 год.

Лабораторна робота 23. Ознаки рівномірної збіжності функціональних

рядів. – 2 год.

Лабораторна робота 24. Властивості сум рівномірно збіжних функціональ-

них рядів. – 2 год.

Лабораторна робота 25. Степеневі ряди. Радіус збіжності. Властивості сум

степеневих рядів. – 2 год.

Лабораторна робота 26. Ряд Тейлора. Розклади основних функцій в ряд

Тейлора-Маклорена. – 2 год.

Лабораторна робота 28. Степеневі ряди в комплексній площині. – 2 год.

Лабораторна робота 29. Контрольна робота. Числові та функціональні

ряди. Степеневі ряди та ряд Тейлора. – 2 год.


Тема 5. Функції обмеженої варіації та інтеграл Стілтьєса.

  1. Монотонні функції та їх властивості. – 2 год.
  2. Функції обмеженої варіації та їх властивості. Теорема Йордана. – 2 год.
  3. Інтеграл Стілтьєса відносно функцій з обмеженою варіацією. – 2 год.
  4. Граничний перехід під знаком інтеграла Стілтьєса. Теорема Хеллі. – 2год.


Лабораторна робота 30. Означення функції обмеженої варіації. Властиво-

сті варіації. – 2 год.

Лабораторна робота 31. Розклад Жордана функції обмеженої варіації. – 2

год.

Лабораторна робота 32. Означення інтеграла Рімана-Стілтьєса. – 2 год.

Лабораторна робота 33. Формула для обчислення інтегралу Рімана-

Стілтьєса. – 2 год.

Лабораторна робота 34. Обзорне заняття за матеріалом другого семестру.

- 2 год.

Самостійна робота – 60 год. (опрацювання лекційного матеріалу і виконання домашніх завдань).


Контрольні запитання і завдання.
  1. Числові ряди. Необхідні умови збіжності. Геометричний ряд. Гармонічний ряд. Узагальнений гармонічний ряд.
  2. Властивості збіжних числових рядів. Залишок ряду. Критерій Коші збіжного ряду.
  3. Критерій збіжності ряду з невід’ємними членами. Теореми порівняння для рядів з невід’ємними членами.
  4. Ознаки д’Аламбера, Коші, логарифмічна та Раабе збіжності рядів з невід’ємними членами.
  5. Інтегральна ознака Маклорена-Коші.
  6. Ряд Лейбніца.
  7. Абсолютно і умовно збіжні ряди.
  8. Властивості абсолютно збіжних рядів.
  9. Знакозмінні ряди. Ознака Лейбніца.
  10. Ознака Діріхле та Абеля збіжності рядів.
  11. Властивості збіжних рядів. Теорема Діріхле. Теорема Рімана.
  12. Добуток рядів. Добуток рядів за Коші, добуток двох абсолютно збіжних рядів.
  13. Нескінченні добутки, збіжність, необхідна умова збіжності. Зв’язок з рядами.
  14. Достатні умови збіжності нескінченних добутків.
  15. Рівномірна збіжність функціональної послідовності. Приклади. Критерій Коші рівномірної збіжності.
  16. Леми про неперервність та інтегрованість граничної функції.
  17. Множина збіжності функціонального ряду. Рівномірна збіжність функціонального ряду. Критерій Коші рівномірної збіжності.
  18. Ознаки Вейєрштраса, Діріхле та Абеля рівномірної збіжності функціонального ряду.
  19. Властивості сум рівномірно збіжних рядів: неперервність, по членне інтегрування, граничний перехід, диференціювання.
  20. Степеневі ряди, радіус збіжності, область збіжності. Теорема Коші-Адамара.
  21. Область рівномірної збіжності степеневого ряду.
  22. Властивості сум степеневих рядів. Теореми про почленне інтегрування та диференціювання степеневого ряду.
  23. Розклад функцій в степеневі ряди. Ряд Тейлора. Теорема про розклад функцій в степеневий ряд.
  24. Приклади розкладу основних функцій в ряди Тейлора-Маклорена.
  25. Ряди з комплексними членами. Степеневі ряди з комплексними членами. Радіус збіжності. Круг збіжності.
  26. Теорема Коші-Адамара для степеневих рядів в комплексній площині.
  27. Показникові функція в комплексній площині. Формули Ейлера.
  28. Монотонні функції і їх властивості. Теорема про представлення монотонної не спадної функції у вигляді суми функції стрибків і монотонно не спадної неперервної функції.
  29. Функції обмеженої варіації і їх властивості. Теорема Жордана.
  30. Інтеграл Стілтьєса відносно монотонно не спадної функції. Критерій інтегрованості.
  31. Класи інтегрованих за Ріманом-Стілтьєсом функцій.
  32. Властивості інтеграла Стілтьєса.
  33. Інтеграл Стілтьєса відносно функцій обмеженої варіації.
  34. Обчислення інтегралів Стілтьєса.
  35. Граничний перехід під знаком інтеграла Стілтьєса. Теорема Хелі.



Система контролю знань


Змістовий модуль 1 – 20 балів;

  • виконання лабораторних робіт (відвідування, активність студента на заняттях, виконання аудиторних та домашніх занять) – 5;
  • письмова контрольна робота – 15;


Змістовий модуль 2 – 20 балів;


  • виконання лабораторних робіт (відвідування, активність студента на заняттях, виконання аудиторних та домашніх занять) – 5;
  • колоквіум – 15;


Змістовий модуль 3 – 20 балів;

  • виконання лабораторних робіт (відвідування, активність студента на заняттях, виконання аудиторних та домашніх занять) – 5;
  • письмова контрольна робота – 15;



Іспит – 40 балів.

Всього за семестр – 100 балів.


Мінімальна кількість балів для зарахування модульної контрольної роботи – 9 балів, для колоквіуму – 9 балів.

Кожна не зарахована контрольна робота може бути переписана один раз.

Колоквіум можна перескласти, якщо він був пропущений з поважної причини.