Рабочая программа учебной дисциплины ф тпу 1- 21/01 федеральное агентство по образованию

Вид материала

Рабочая программа

Содержание Высшая математика Всего аудиторных занятий 309,5 часа 2009 г. Предисловие ЕН.1. Высшая математика Курс 1,2 (1,2,3 семестр – экзамен) I. линейная и векторная алгебры Ii. аналитическая геометрия Iii дифференциальное исчисление функции одной независимой переменной Iv дифференциальное исчисление функции V интегральное исчисление функции одной переменной 5.3.Несобственные интегралы (2) Vi числовые и функциональные ряды Vii дифференциальные уравнения и системы. Viii теория функций комплексного переменного Ix элементы теории вероятностей математической I линейная и векторная алгебры Ii аналитическая геометрия Iii дифференциальное исчисление функции одной Iv дифференциальное исчисление функции V интегральное исчисление функции одной ... Полное содержание

Подобный материал:

• Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 85.92kb.
• Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 101.07kb.
• Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 129.5kb.
• Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 107.65kb.
• Рабочая программа учебной дисциплины ф тпу 1- 21/01 федеральное агентство по образованию, 334.33kb.
• Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 187.41kb.
• Рабочая программа учебной дисциплины ф тпу 21/01 Федеральное агентство по образованию, 307.9kb.
• Рабочая программа учебной дисциплины ф тпу 1-21/01 федеральное агентство по образованию, 217.64kb.
• Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 236.22kb.
• Рабочая программа учебной дисциплины ф тпу 1-21/01 федеральное агентство по образованию, 266.17kb.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

«ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»


«УТВЕРЖДАЮ»

Декан ФТФ

В.И.Бойко

«___»__________2009 г.


ВЫСШАЯ МАТЕМАТИКА


Рабочая программа для специальности

240601– химическая технология материалов современной энергетики


Факультет - физико-технический (ФТФ)

Обеспечивающая кафедра «Высшая математика и математическая физика»


Курс I,II Семестр I, II, III

Учебный план набора 2009 года


Распределение учебного времени


лекции 124 часа

практические занятия 185,5 часов


Всего аудиторных занятий 309,5 часа


Самостоятельная (внеаудиторная)

работа 290 часов


Общая трудоемкость 599,5 часа


Экзамен в 1, 2, 3 семестрах


2009 г.

Предисловие

1. Рабочая программа составлена на основе ГОС ВПО по специальности:

240601 (250900) – химическая технология материалов современной энергетики утвержденного Министерством образования РФ 27.03.2000 года рег. № 225 тех/дс.


РАССМОТРЕНА и ОДОБРЕНА на заседании обеспечивающей кафедры «Высшей математики и математической физики» 28.08.2009 г. протокол № 121


2. Разработчик

доцент ВММФ ___________ Терехина Л.И.


Зав. обеспечивающей кафедрой

ВММФ

_________________ А.Ю. Трифонов


3. Рабочая программа СОГЛАСОВАНА с «Физико-техническим факультетом» ТПУ, выпускающей кафедрой.

СООТВЕТСТВУЕТ действующему учебному плану.


Заведующий выпускающей кафедры 43 ___________ В.П.Дмитриенко

Аннотация

Высшая математика

ЕН.1. Высшая математика

240601

Кафедра ВММФ ЕНМФ

доцент кафедры ВММФ, ЕНМФ, к.ф.-м.н., Терехина Л.И.


Цель: формирование знаний о математике, как особом способе познания мира и образе мышления, общности её понятий и представлений, дать опыт построения математических моделей и проводить необходимые расчёты в рамках построенных моделей; употребления математической символики для выражения количественных и качественных отношений объектов.


Содержание: Системы линейных уравнений. Определители. Системы векторов, ранг матрицы. N – мерное линейное векторное пространство. Элементы аналитической геометрии на прямой, плоскости и в трехмерном пространстве. Линейные операторы и матрицы. Собственные векторы линейных операторов. Преобразование систем координат. Кривые и поверхности второго порядка.

Элементы аналитической геометрии на прямой, плоскости и в трехмерном пространстве.

Множества; вещественные числа; логическая символика; понятие функции и её свойства; числовые последовательности; предел функции и его свойства; бесконечно малые и бесконечно большие функции и их сравнение; непрерывность функции и классификация точек разрыва; замечательные пределы; производная и правила дифференцирования; дифференциал; правило Лопиталя; применение к исследованию функции; формула Тейлора; функция нескольких переменных; частные производные; экстремум функции нескольких переменных; скалярное поле и его геометрические характеристики; производная по направлению; градиент.

Первообразная; свойства неопределенных интегралов; основные методы интегрирования рациональных, тригонометрических и иррациональных функций; определенный интеграл, его свойства, геометрические и физические приложения; несобственные интегралы; кратные интегралы и их вычисление в разных системах координат; криволинейные интегралы; поверхностные интегралы; основные характеристики векторных полей.

Дифференциальные уравнения первого порядка; дифференциальные уравнения высших порядков; системы дифференциальных уравнений.

Числовые ряды; сумма ряда; свойства сходящихся рядов; необходимые и достаточные признаки сходимости числовых рядов; знакочередующиеся ряды; условная и абсолютная сходимость; функциональные и степенные ряды; интервал и радиус сходимости; ряды Тейлора и Маклорена. Функции комплексного переменного; условия Коши-Римана; интегральная формула Коши. Элементарная теория вероятностей, математические основы теории вероятностей, модели случайных процессов, проверка гипотез, принцип максимального правдоподобия, статистические методы обработки экспериментальных данных, устойчивые методы оценивания.


Рабочая программа курса «Высшая математика», предназначенного для студентов первого и второго курса ФТФ специальности 240601– химическая технология материалов современной энергетики, составлена в соответствии с государственными образовательными стандартами и образовательным стандартом Томского политехнического университета.

Курс 1,2 (1,2,3 семестр – экзамен)

Всего 599,5 ч., в т.ч.: ЛК –124 ч., ПР – 185,5 ч., СР – 290 ч.


Цели и задачи преподавания дисциплины

«Высшая математика»

Цели дисциплины:

Современный научный сотрудник или инженер, в достаточной мере, должен владеть математическими методами исследования и логической культурой мышления. Высшая математика является одной из фундаментальных дисциплин для студентов технических специальностей, которая позволит сформировать у студента навыки решения задач физического профиля с использованием математического аппарата дисциплины. Дисциплина Дисциплина базируется на знании школьного курса математики , может являться пререквизитом к изучению ряда специальных дисциплин.

Целью изучения дисциплины студентами является приобретение знаний, предусмотренных программой, формированием умения и навыков применять полученные знания при решении конкретных задач.


Студент, изучив дисциплину «Высшая математика» должен:

иметь представление:

• о математике, как особом способе познания мира и образе мышления,
  

общности её понятий и представлений;

• о связи курса с другими дисциплинами;
  

уметь:

• использовать основные понятия и методы линейной алгебры, аналитической геометрии;
  
• использовать основные понятия и методы дифференциального исчисления функции одной и нескольких независимых переменных;
  
• использовать основные понятия и методы интегрального исчисления функции одной и нескольких независимых переменных;
  
• использовать математические модели для конкретных процессов и проводить необходимые расчёты в рамках построенных моделей;
  
• использовать полученные знания при усвоении учебного материала последующих дисциплин.
  

Знать и иметь опыт:

• употребления математической символики для выражения количественных и качественных отношений объектов;
  
• применения математических методов и элементов научных исследований в прикладных задачах и оценивания пределов применимости полученных результатов.
  

Задачи дисциплины:

В результате изучении дисциплины «Математика» студент обязан:

• Иметь представление:
  
  • о математике, как особом способе познания мира и образе мышления, общности её понятий и представлений;
    
  • о логической символике, используемой в данной и последующих дисциплинах;
    
  • о методе сечений;
    
  • о канонических уравнениях поверхностей второго порядка, (сфера, эллипсоид, параболоиды, гиперболоиды, цилиндры, конусы).
    
  • о множествах и операциях над ними;
    
  • о функциональной связи переменных и её свойствах
    
  • классах интегрируемых функций;
    
  • о применении интегрального исчисления к изучению векторных полей;
    
  • о “неберущихся” интегралах;
    
  • о классификации дифференциальных уравнений;
    
  • об общем и частном решении дифференциального уравнения;
    
  • об особых решениях уравнений;
    
  • методах решения дифференциальных уравнений;
    
  • линейных неоднородных дифференциальных уравнениях высших порядков и способах их решения;
    
  • методах решения систем дифференциальных уравнений;
    
  • числовых и функциональных рядах и условиях их сходимости;
    
  • функциях комплексного переменного и их свойствах;
    

• Уметь:
  
  • вычислять определители n – го порядка различными способами;
    
  • вычислять ранг матрицы различными способами;
    
  • пользуясь понятием ранга матрицы, находить базис линейного пространства, исследовать систему линейных уравнений на совместность;
    
  • производить действия над векторами в пространствах 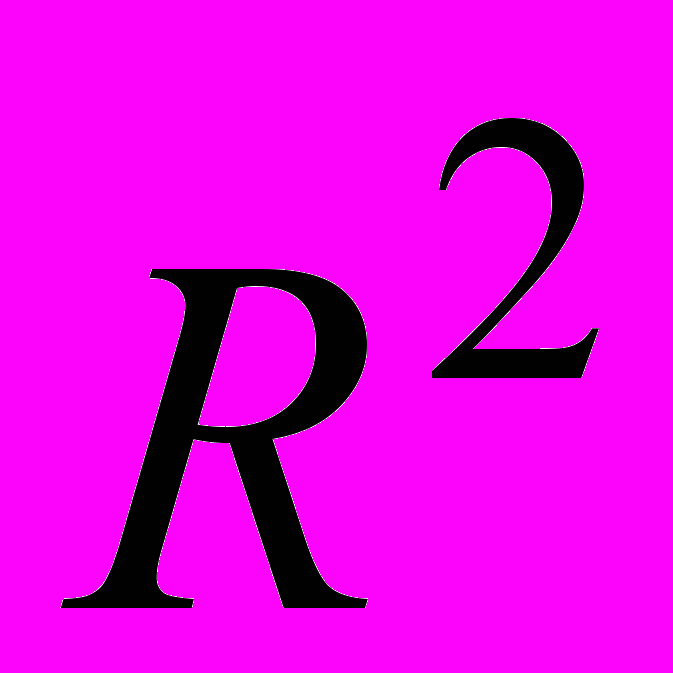, 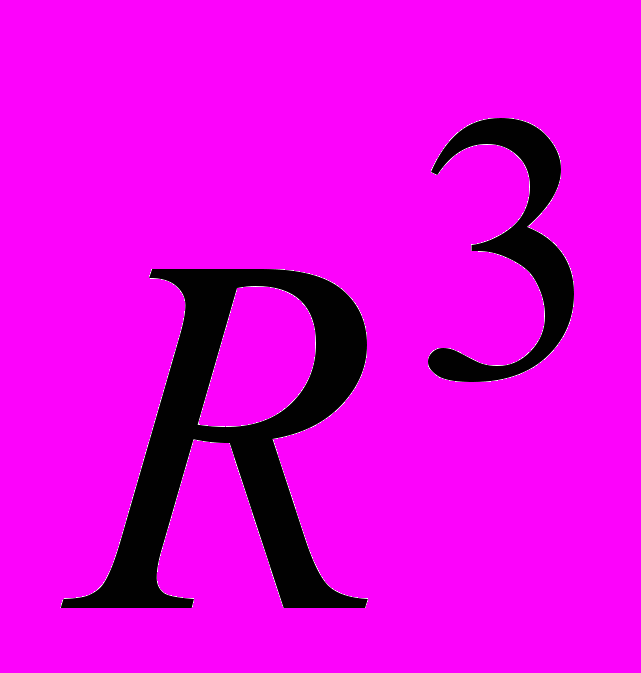и находить разложение произвольного вектора по любому базису;
    
  • определять размерность пространства, подпространства;
    
  • исследовать систему n линейных алгебраических уравнений с m неизвестными; решать систему методами Крамера, Гаусса, с помощью обратной матрицы;
    
  • находить фундаментальную систему решений однородной системы уравнений;
    
  • геометрически и аналитически представлять прямую и плоскость в пространстве ;
    
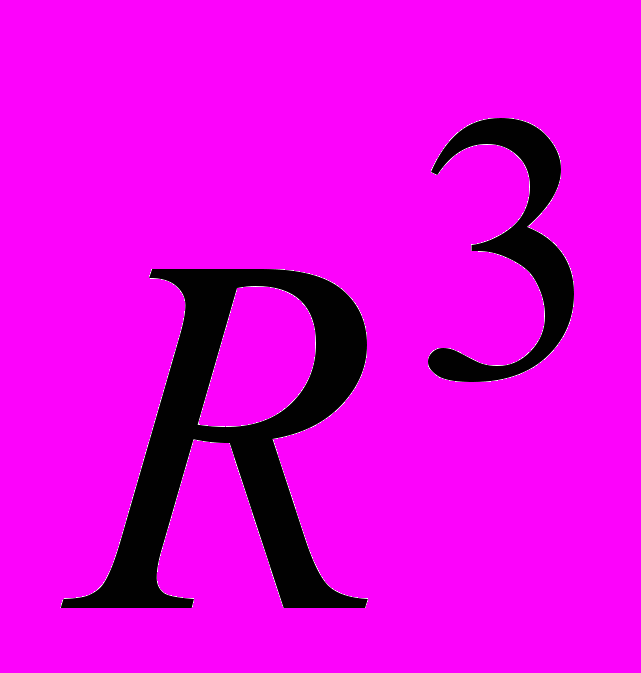  • использовать аппарат векторной алгебры для анализа взаимного положения прямых и плоскостей;
    
  • приводить общие уравнения прямой в пространстве к каноническому виду;
    
  • выводить канонические уравнения кривых второго порядка (окружность, эллипс, гипербола, парабола);
    
  • приводить общее уравнение кривой второго порядка к каноническому виду;
    
  • применять методы дифференциального исчисления функций одной и нескольких переменных к отысканию физических и геометрических характеристик процессов
    
  • применять методы интегрального исчисления функций одной и нескольких переменных к отысканию физических и геометрических характеристик процессов;
    
  • определять тип дифференциального уравнения и выбирать метод его решения;
    
  • выбрать метод решения системы дифференциальных уравнений;
    
  • составить дифференциальное уравнение, описывающее конкретный физический процесс;
    
  • выбирать критерии сходимости числовых рядов;
    
  • находить интервалы сходимости степенных рядов;
    
  • самостоятельно овладевать новыми математическими знаниями, опираясь на опыт, приобретенный в процессе изучения курса «Математика»;
    
  • использовать полученные знания при освоении учебного материала последующих дисциплин.
    

• Знать и иметь опыт:
  
  • место дисциплины «Высшая математика» среди других, изучаемых студентом дисциплин и её значение при изучении последующих курсов;
    
  • работы с учебной и справочной литературой,
    
  • определение матрицы, основные типы матриц, алгебру матриц, основные характеристики матриц: определение и свойства определителей n – го порядка;
    
  • определение ранга матрицы, его свойства;
    
  • определение вектора как элемента точечно-векторного пространства, принципы построения алгебры векторов;
    
  • способы задания прямой на плоскости и в пространстве;
    
  • определение линейного пространства 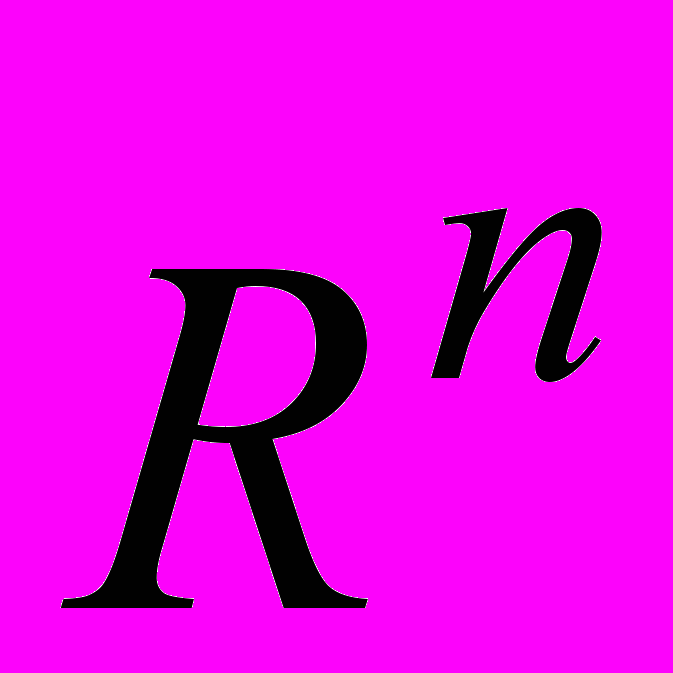и его основные свойства;
    
  • геометрические определения кривых второго порядка (окружность, эллипс, гипербола, парабола);
    
  • нахождения производных от функций одной и нескольких переменных,
    
  • исследование функций на экстремум и монотонность;
    
  • нахождение пределов;
    
  • применение методов дифференциального и интегрального исчисления к решению физических задач;
    
  • вычисления неопределенных интегралов;
    
  • вычисления или оценки определенных интегралов;
    
  • определять тип дифференциального уравнения и выбирать метод его решения;
    
  • составить дифференциальное уравнение, описывающее конкретный физический процесс;
    
  • критерии сходимости числовых рядов;
    
  • ряды Тейлора и Маклорена и условия разложения функций;
    
  • опрелеления интервала сходимости степенного ряда.
    

Задачи изложения и изучения дисциплины

Для достижения целей, поставленных при изучении дисциплины, используется набор методических средств:

• лекции;
  
• практические занятия с опросом студентов и закреплением теоретического материала;
  
• индивидуальные задания;
  
• работа с учебниками в библиотеке по изучению разделов дисциплины, вынесенных на самостоятельное изучение
  
• индивидуальные и групповые консультации по теоретическим и практически вопросам курса;
  

Проверка приобретенных знаний, навыков и умений осуществляется посредством опроса студентов, текущих тестовых испытаний, контрольных работ, теоретических коллоквиумов и сдачи зачета.


Содержание теоретической части дисциплины


П Е Р В Ы Й С Е М Е С Т Р (лекц. - 46 час., пр. зан. - 72 час., сам. раб. 90 час.)


I. ЛИНЕЙНАЯ И ВЕКТОРНАЯ АЛГЕБРЫ (14)

1.1. Матрицы , определители., системы линейных уравнений. (8)

Определители, их свойства и вычисление. Матрицы и действия над ними. Линейные операции над матрицами. Умножение матриц. Ранг матрицы. Обратная матрица. Решение матричных уравнений. Система линейных алгебраических уравнений. Методы матричный, Крамера, Гаусса. Однородные системы, тривиальное и нетривиальные решения. Фундаментальная система решений. Собственные значения и собственные векторы матрицы.

1.2. Векторная алгебра (6)

Основные понятия векторной алгебры. Линейные операции над векторами в геометрической форме. Линейная зависимость и линейная независимость системы векторов. Понятие базиса векторного пространства, размерность векторного пространства. Декартовый базис, координаты вектора. Проекция вектора, орт вектора, направляющие косинусы вектора. Простейшие задачи векторной алгебры. Скалярное, векторное и смешанное произведения векторов. Определение, свойства, запись в координатной форме, приложения. Некоторые физические приложения векторной алгебры.


II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ (8)

2.1. Геометрия на плоскости(4)

Прямая линия на плоскости. Различные виды уравнений прямой. Взаимной расположение прямых на плоскости. Нахождение расстояния от точки до прямой. Кривые второго порядка. Основные типы кривых и их канонические уравнения. Построение кривых по каноническим уравнениям. Приведение уравнений кривых второго порядка к каноническому виду. Построение линий в полярной системе координат и линий, заданных параметрически.

2. Геометрия в пространстве(4)
   

Плоскость. Основные уравнения плоскости. Взаимное расположение плоскостей. На хождение расстояния от точки до плоскости. Прямая линия в пространстве. Общие, канонические и параметрические уравнения прямых. Взаимное расположение прямых в пространстве. Расстояние от точки до прямой в пространстве. Совместное расположение прямой и плоскости в пространстве. Поверхности второго порядка. Типы поверхностей и их канонические уравнения. Построение поверхностей.


III ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ (24).

1. Предел и непрерывность функции (8 ).
   

Предмет анализа. Функция, способы задания. Основные элементарные функции, их графики и области определения. Гиперболические функции. Понятие сложной и обратной функции. Бесконечно малые и бесконечно большие величины. Предел функции, его геометрический смысл. Предел последовательности. Теоремы о пределах. Замечательные пределы. Сравнение бесконечно малых величин. Эквивалентные бесконечно малые величины, основные соотношения эквивалентности. Неопределенности и методы их раскрытия. Односторонние пределы. Непрерывность в точке и на интервале. Классификация точек разрыва. Теоремы о непрерывных функциях.

3.2. Производная функции одной переменной (8 ).

Задача о касательной. Средняя и мгновенная скорость. Приращение аргумента и приращение функции. Понятие производной функции. Физический и геометрический смысл производной. Связь непрерывности и дифференцируемости функции. Правила дифференцирования. Таблица производных. Метод логарифмического дифференцирования. Дифференцирование показательно-степенной, неявной и параметрически заданной функции. Дифференциал функции, его математический, геометрический и физический смысл. Свойства дифференциала, инвариантность его формы. Применение дифференциала к приближенным вычислениям. Производные и дифференциалы высших порядков. Теоремы о дифференцируемых функциях (Ферма, Ролля, Лагранжа, Коши).

3.3. Приложения производной (8 ).

Правило Лопиталя. Возрастание и убывание функции на интервале. Экстремумы. Необходимое и достаточные условия существования экстремума функции. Наименьшее и наибольшее значения на отрезке. Задачи смыслового содержания. Выпуклость, вогнутость кривой, точки перегиба, необходимое и достаточное условия. Асимптоты, понятие, виды асимптот. Схема отыскания вертикальных асимптот. Нахождение параметров наклонных асимптот. Полное исследование функции и построение графиков. Касательная и нормаль к кривой. Геометрические и физические приложения.


В Т О Р О Й С Е М Е С Т Р (лекц. - 34 час., пр. зан. - 60 час., сам. Раб. - 118 час.)

IV ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ

НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ (6).

4.1. Функции нескольких переменных (6).

Понятие функции нескольких независимых переменных. Область определения. Предел и непрерывность. Частные производные, их геометрический смысл. Частные и полный дифференциалы. Производная сложной функции. Полная и частная производные. Неявные функции и их дифференцирование. Производные и дифференциалы высших порядков. Инвариантность формы полного дифференциала. Геометрический смысл полного дифференциала функции двух переменных. Приложение дифференциала к приближенным вычислениям. Экстремум функции двух независимых переменных, понятие, необходимые и достаточные условия. Седловые точки. Наибольшее и наименьшее значения функции двух переменных в замкнутой области. Касательная плоскость и нормаль к поверхности. Векторная функция скалярного аргумента. Понятие, дифференцирование, касательная к пространственной кривой. Метод наименьших квадратов.


V ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ (18)

5.1. Неопределенный интеграл (8 )

Первообразная. Неопределенный интеграл, его геометрический смысл. Инвариантность формы. Таблица интегралов. Основные методы интегрирования: непосредственное интегрирование, метод подведения под знак дифференциала, метод подстановки, метод интегрирования по частям. Циклические интегралы. Интегрирование некоторых классов функций: содержащих квадратный трехчлен в знаменателе дроби, рациональных дробей, простейших иррациональных функций, дифференциальных биномов. Неберущиеся интегралы.

5.2. Определенный интеграл (8 )

Задачи, приводящие к понятию определенного интеграла. Определенный интеграл, существование, свойства. Геометрический смысл. Теорема о среднем значении функции в интервале, геометрический смысл теоремы. Оценка интеграла. Интеграл с переменным верхним пределом. Формула Ньютона - Лейбница. Связь между неопределенным и определенным интегралами. Методы вычисления определенного интеграла: подстановка и интегрирование по частям. Общая схема применения определенного интеграла в решении задач геометрии и физики. Площадь плоской фигуры в прямоугольных и полярных координатах. Вычисление объема по площади поперечного сечения, объем тела вращения. Вычисление длины дуги кривой в прямоугольных и полярных координатах. Вычисление площади поверхности вращения. Приложения определенного интеграла к решению задач физики, механики и др.

5.3.Несобственные интегралы (2)

Несобственные интегралы по бесконечному промежутку (I -го рода) и от неограниченной функции (II-го рода). Исследование на сходимость. Абсолютная и условная сходимость.


VI ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ (10 )

6.1. Числовые ряды. (4)

Понятие числового ряда, сумма ряда. Необходимый признак сходимости. Достаточные признаки сходимости знакоположительных рядов. Знакопеременные и знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость.

6.2. Ряды Тейлора . (6 )

Понятие функционального ряды. Область сходимости. Равномерная сходимость. Признак Вейерштрасса. Степенные ряды. Теорема Абеля. Радиус и интервал сходимости. Ряды Тейлора и Маклорена. Представление элементарных функций степенными рядами. Использование степенных рядов в приближенных вычислениях.


Т Р Е Т И Й С Е М Е С Т Р (лекц. - 44 час., практ. зан. - 54 час., сам. Раб. - 82 час.)


VII ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И СИСТЕМЫ. (16)

7.1. Дифференциальные уравнения первого порядка. (8)

Понятие дифференциальных уравнений. Общее и частное решения, их геометрический смысл. Уравнения с разделяющимися переменными. Однородные дифференциальные уравнения. Линейные дифференциальные уравнения. Уравнения Бернулли. Уравнения в полных дифференциалах. Интегрирующий множитель.


7.2. Дифференциальные уравнения высших порядков. (6)

Общие понятия. Задача Коши. Геометрический смысл общего и частного решения дифференциального уравнения 2-го порядка. Случаи понижения порядка. Общая теория линейных однородных и неоднородных дифференциальных уравнений. Линейные уравнения с постоянными коэффициентами. Метод неопределенных коэффициентов и метод вариации постоянных. Уравнения Эйлера.

7.3. Системы линейных дифференциальных уравнений . (2)

Нормальные системы дифференциальных уравнений. Общая теория систем линейных дифференциальных уравнений. Системы линейных однородных и неоднородных дифференциальных уравнений с постоянными коэффициентами. Решение систем методом исключения. Метод Эйлера (метод характеристических уравнений). Применение дифференциальных уравнений и систем к решению задач химической кинетики.


VIII ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО (12 )

8.1. Комплексные числа и функции комплексного переменного. (6)

Понятие комплексного числа. Модуль и аргумент числа. Формы записи комплексных чисел. Действия над комплексными числами. Элементарные функции комплексной переменной. Области на комплексной плоскости. Алгебраические уравнения.

8.2. Дифференцирование и интегрирование функции. (6)

Производная функции комплексного переменного и ее геометрический смысл. Условия Коши - Римана. Понятие и свойства аналитической функции. Определение аналитической функции по вещественной или мнимой части. Гармонические функции. Определение интеграла по комплексной переменной и его свойства. Интегрирование аналитических функций. Теорема Коши. Интегральная формула Коши.

IX ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ МАТЕМАТИЧЕСКОЙ

СТАТИСТИКИ (16)

9.1. Случайные события. (8 )

Виды случайных событий. Классическое, статистическое и геометрическое определение вероятности случайного события. Теоремы сложения и умножения вероятностей. Полная вероятность. Вероятность гипотезы (формула Байеса). Повторные независимые испытания, формулы Бернулли, Муавра-Лапласа, Пуассона.

9.2. Случайные величины. (6)

Дискретные и непрерывные случайные величины. Интегральная и дифференциальная (плотность вероятности) функции распределения случайных величин. Числовые характеристики распределения случайной величины: математическое ожидание, дисперсия, начальные и центральные моменты. Функция случайного аргумента, закон ее распределения. Примеры распределений (равномерное, Пуассона, нормальное, экспоненциальное, Рэлея, Максвелла). Закон больших чисел. Неравенство и теорема Чебышева. Теорема Бернулли.

9.3. Элементы математической статистики. (2)

Случайная выборка, полигон, гистограмма. Точечная и интервальная оценка среднего значения и дисперсии величины. Проверка гипотез о законе распределения случайной величины, Критерий Пирсона.


Содержание практических занятий.


П Е Р В Ы Й С Е М Е С Т Р ( ауд. - 72 часа, внеауд. - 90 часов)


I ЛИНЕЙНАЯ И ВЕКТОРНАЯ АЛГЕБРЫ ( 20)

1. Матрицы , определители., системы линейных уравнений. (12 час.)
   

Вычисление определителей.

Линейные операции над матрицами. Умножение матриц. Ранг матрицы. Обратная матрица. Решение матричных уравнений.

Методы матричный и Крамера решения определенных квадратных систем линейных уравнений 3-го порядка.

Метод Гаусса. Решение определенных и неопределенных систем.

Однородные системы, тривиальное и нетривиальные решения. Фундаментальная система решений. Собственные значения и собственные векторы матриц.

Контрольная работа «Линейная алгебра.»

Индивидуальное домашнее задание 1 «Линейная алгебра».


1.2. Векторная алгебра (8 час.)

Линейные операции над векторами в геометрической и координатной формах.

Скалярное и векторное произведения векторов.

Смешанное произведение векторов.

Контрольная работа «Векторная алгебра»

Индивидуальное домашнее задание 2 «Векторная алгебра».


II АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ (16 )

1. Геометрия на плоскости (8 час.)
   

Прямая линия на плоскости. Нахождение расстояния от точки до прямой.

Построение кривых по каноническим уравнениям. Приведение уравнений кривых второго порядка к каноническому виду.

Построение линий в полярных координатах и линий, заданных параметрически.

Контрольная работа «Аналитическая геометрия на плоскости» .

Индивидуальное задание 3 «Аналитическая геометрия на плоскости» .

2. Геометрия в пространстве (8 час.)
   

Плоскость и прямая в пространстве.

Поверхности второго порядка.

Контрольная работа «Аналитическая геометрия в пространстве» .

Индивидуальное задание 4 «Аналитическая геометрия в пространстве» .


III ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ

НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ (36 ).

3.1. Предел и непрерывность функции (10 час.)

Предел функции. Предел последовательности.

Эквивалентные бесконечно малые величины.

Непрерывность функции.

Контрольная работа «Предел и непрерывность функции»

Индивидуальное домашнее задание 5 «Предел. Непрерывность».


3.2. Производная функции одной переменной (12 час.)

Понятие производной функции. Физический и геометрический смысл производной.

Дифференцирование сложных, неявных, параметрически заданных функций.

Дифференциал функции. Высшие производные.

Контрольная работа «Производная» .

Индивидуальное домашнее задание 6 «Производная».


3.3. Приложения производной (14 час.)

Правило Лопиталя.

Экстремумы. Наименьшее и наибольшее значения на отрезке. Геометрический смысл производной.

Задачи смыслового содержания.

Выпуклость, вогнутость кривой, точки перегиба.

Асимптоты.

Полное исследование функции и построение графиков.

Контрольная работа «Приложение производной»

Индивидуальное домашнее задание 7 «Приложение производной».


В Т О Р О Й С Е М Е С Т Р (ауд. – 60 часов, самост. - 118 часов)


IV ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ

НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ (10 ).

1. Функции нескольких переменных (10 час.)
   

Область определения функции. Частные производные.

Частные производные. Полное приращение и дифференциал. Производные и дифференциалы высших порядков.

Экстремум функции . Критические точки и их характер.

Касательная плоскость и нормаль к поверхности. Производная по направлению, градиент.

Контрольная работа «Функции нескольких переменных» .

Индивидуальное домашнее задание 8 «Функции нескольких переменных».


V ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ

НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ (30)

5.1. Неопределенный интеграл (16 час.)

Табличное интегрирование. Интегрирование «подведением под знак дифференциала»

Интегрирование «по частям». Метод подстановки.

Интегрирование рациональных дробей.

Интегрирование иррациональных и тригонометрических функций.

Контрольная работа «Неопределенный интеграл» .

Индивидуальное домашнее задание 9 «Неопределенный интеграл» .

5.2. Определенный и несобственные интегралы (14 час.)

Вычисление определенных интегралов. Оценка интеграла.

Вычисление площадей плоских фигур, объемов тел, длин дуг.

Несобственные интегралы, их вычисление и оценка.

Физические приложения интеграла.

Контрольная работа «Определенный и несобственные интегралы» .

Индивидуальное домашнее задание 10 «Определенный интеграл» .


VI ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ ( 20)

6.1. Числовые ряды. (10 час)

Знакомство с числовыми рядами. Сходимость числовых рядов. Нахождение сумм некоторых числовых рядов.

Исследование на сходимость знакоположительных рядов.

Знакочередующиеся ряды. Нахождение суммы ряда и оценка ее точности.

Контрольная работа «Числовые ряды»

6.2. Функциональные ряды. Ряды Тейлора. (10 час.)

Функциональные ряды, интервал сходимости, равномерная и абсолютная сходимость.

Ряды Тейлора и Маклорена. Представление элементарных функций степенными рядами.

Приложение рядов Тейлора к приближенным вычислениям.

Контрольная работа "Функциональные ряды, ряды Тейлора" .

Индивидуальное домашнее задание 15 «Числовые и функциональные ряды».


Т Р Е Т И Й С Е М Е С Т Р (ауд. -54 часа, самост. - 82 часа)


VII ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И СИСТЕМЫ. (26)

7.1. Дифференциальные уравнения первого порядка. (12 час.)

Уравнения с разделяющимися переменными. Задача Коши.

Однородные уравнения первого порядка и уравнения, приводящиеся к однородным.

Линейные уравнения и уравнения типа Бернулли.

Уравнения в полных дифференциалах. Интегрирующий множитель.

Представление частных решений уравнения степенными рядами.

Контрольная работа «Дифференциальные уравнения 1-го порядка» .

Индивидуальное задание 14-1 «Дифференциальные уравнения I-го порядка»

7.2. Дифференциальные уравнения высших порядков. (10 час.)

Уравнения, допускающие понижение порядка.

Линейные однородные уравнения с постоянными коэффициентами.

Линейные неоднородные уравнения. Метод вариации.

Метод неопределенных коэффициентов решения линейных неоднородных

уравнений с правой частью специального вида.

Уравнения Эйлера.

Контрольная работа "Линейные дифференциальные уравнения" .

7.3. Системы линейных дифференциальных уравнений . (4 час.)

Решение систем однородных линейных уравнений методами исключения и Эйлера.

Неоднородные линейные дифференциальные системы.

Контрольная работа "Линейные дифференциальные системы»"

Индивидуальное задание 14-2 «Дифференциальные уравнения и системы» .


VIII ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО (10)

8.1. Комплексные числа и функции комплексного переменного. (10 час.)

Комплексные числа и действия над ними.

Элементарные функции комплексного переменного. Вычисление значений функций, решение уравнений. Линии и области на комплексной плоскости.

Дифференцирование функции комплексного переменного. Условия Коши - Римана.

Геометрический смысл производной. Отображения элементарными функциями.

Интегрирование функций комплексного переменного.

Контрольная работа «Комплексные числа и функции» .

Индивидуальное домашнее задание 16 «Комплексные числа и функции» .


IX ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ

СТАТИСТИКИ (18)

9.1. Случайные события. (6 час.)

Случайные события. Классическая и геометрическая вероятности.

Теоремы сложения и умножения вероятностей.

Полная вероятность события. Переоценка вероятностей гипотез при свершившихся

событиях. Формула Байеса.

Повторные независимые испытания, схема Бернулли. Формулы Муавра - Лапласа и

Пуассона.

9.2. Случайные величины. (8 час.)

Дискретные и непрерывные случайные величины. Закон распределения. Математическое ожидание и дисперсия случайной величины.

Равномерное распределение. Экспоненциальное распределение. Распределение Пуассона. Примеры. Нормальное распределение и распределения, связанные с нормальным (Рэлея, Максвелла и т.д.). Примеры.

Контрольная работа: «Теория вероятностей" .

3. Элементы математической статистики. (4)
   

Случайная выборка, полигон, гистограмма. Точечная и интервальная оценка среднего значения и дисперсии величины. Проверка гипотез о законе распределения случайной величины, Критерий Пирсона.

Индивидуальное домашнее задание 18 «Теория вероятностей и математическая статистика».